25-GRPO IS SECRETLY A PROCESS REWARD MODEL

过程集 λ	共享前缀	e(λ)（最长前缀长度）	父节点	s(λ)（父节点的 e）
λ0=G	[a,b]	2（前 2 个令牌相同）	根节点（无父）	0
λ1={g(2),g(3)}	[a,b,e]	3（前 3 个令牌相同）	λ0	e(λ0)=2
λ2={g(1)}	[a,b,c,d]	4（自身全长）	λ0	e(λ0)=2
λ3={g(2)}	[a,b,e,f]	4（自身全长）	λ1	e(λ1)=3
λ4={g(3)}	[a,b,e,g]	4（自身全长）	λ1	e(λ1)=3

步骤 3：计算过程集的步骤级奖励 R^(λ)

R^(λ) 是该集合中所有轨迹的平均结果级奖励：

R^(λ0)=3r1+r2+r3=（8+6+4）/3=6
R^(λ1)=2r2+r3=（6+4）/2=5
R^(λ2)=1r1=8
R^(λ3)=1r2=6
R^(λ4)=1r3=4

步骤 4：确定每个令牌的步骤级奖励 Ri,t

每个令牌 gt(i)（第 i 条轨迹的第 t 个令牌，t 从 0 开始）属于唯一的过程集 λ(i,t)，其奖励 Ri,t=R^(λ(i,t))。

具体分配（结合 s(λ)≤t<e(λ) 规则）：

g(1) 的令牌：
- t=0,1：属于 λ0（0≤t<2）→ R1,0=R1,1=6
- t=2,3：属于 λ2（2≤t<4）→ R1,2=R1,3=8
g(2) 的令牌：
- t=0,1：属于 λ0 → R2,0=R2,1=6
- t=2：属于 λ1（2≤t<3）→ R2,2=5
- t=3：属于 λ3（3≤t<4）→ R2,3=6
g(3) 的令牌：
- t=0,1：属于 λ0 → R3,0=R3,1=6
- t=2：属于 λ1 → R3,2=5
- t=3：属于 λ4 → R3,3=4

总结

这个例子清晰展示了：

如何通过 "共享前缀" 划分过程集 B(G)，形成树结构；
如何基于过程集计算步骤级奖励（将结果奖励 "分解" 到中间步骤）；
如何通过优势函数将步骤奖励标准化，用于 GRPO 的损失计算。

这正是 GRPO "隐藏 PRM" 的核心：无需人工标注中间步骤奖励，而是通过轨迹间的重叠前缀自动生成步骤级信号。

GRPO存在的问题

从过程集划分\(X_t\)的角度来看 GRPO 的目标函数（参见式 6），我们注意到：每条轨迹在索引t处对损失的贡献，与过程集中其他所有轨迹的贡献相同（其中，的定义见式 5）。

每个过程集对总损失的贡献会被\(|\lambda|\)（集合大小）缩放：这存在损害探索（当时）和利用（当时）的风险。

考虑某个的过程集\(\lambda\)：

若，则 GRPO 下策略分配给\(\lambda\)对应过程步骤的概率增量会被\(|\lambda|\)放大，这会降低后续训练轮次中探索与不同的过程步骤的可能性；
相反，若，则 GRPO 下分配给\(\lambda\)的概率减量会被放大，这会降低利用\(\lambda\)中高奖励轨迹的可能性。

为说明这一点，考虑图 1 中的组G，假设\(r_1 = r_2 = r_6 = 0.5\)，\(r_4 = r_5 = 0\)，\(r_3 = 1\)，且令。此时：尽管\(g^{(3)}\)的奖励最高，但在 GRPO 目标函数下，子轨迹\(g^{(3)}_{:4}\)的概率会降低，进而降低生成补全结果\(g^{(3)}\)的整体可能性。式 7 中的项会将这种概率降低幅度放大 3 倍（因\(|\lambda| = 3\)）。

我们提议将令牌级损失按缩放（即\(\lambda\)-GRPO；式 8）：这能抵消式 7 中的\(|\lambda|\)项，使每个过程集在索引t处对损失的贡献相等。

核心逻辑说明

GRPO 原目标函数中，过程集的损失贡献会被其大小\(|\lambda|\)放大，导致：

大集合的正优势会过度抑制探索（只聚焦该集合）；
大集合的负优势会过度打压其中的高奖励轨迹（连带着好轨迹一起被削弱）。

通过引入的缩放因子，平衡了不同大小过程集的损失贡献，解决了上述缺陷。

例子：

总结

在我们的例子中，GRPO 因的放大效应，会对含 2 条轨迹的\(\lambda_1\)过度惩罚，连带降低中等奖励轨迹的概率；而 λ-GRPO 通过除以\(|\lambda|\)，让每个过程集的损失贡献不受大小影响，既保护了探索，也避免了对优质轨迹的误打压。这就是 λ-GRPO 能提升性能和训练速度的核心原因。

实验结果：

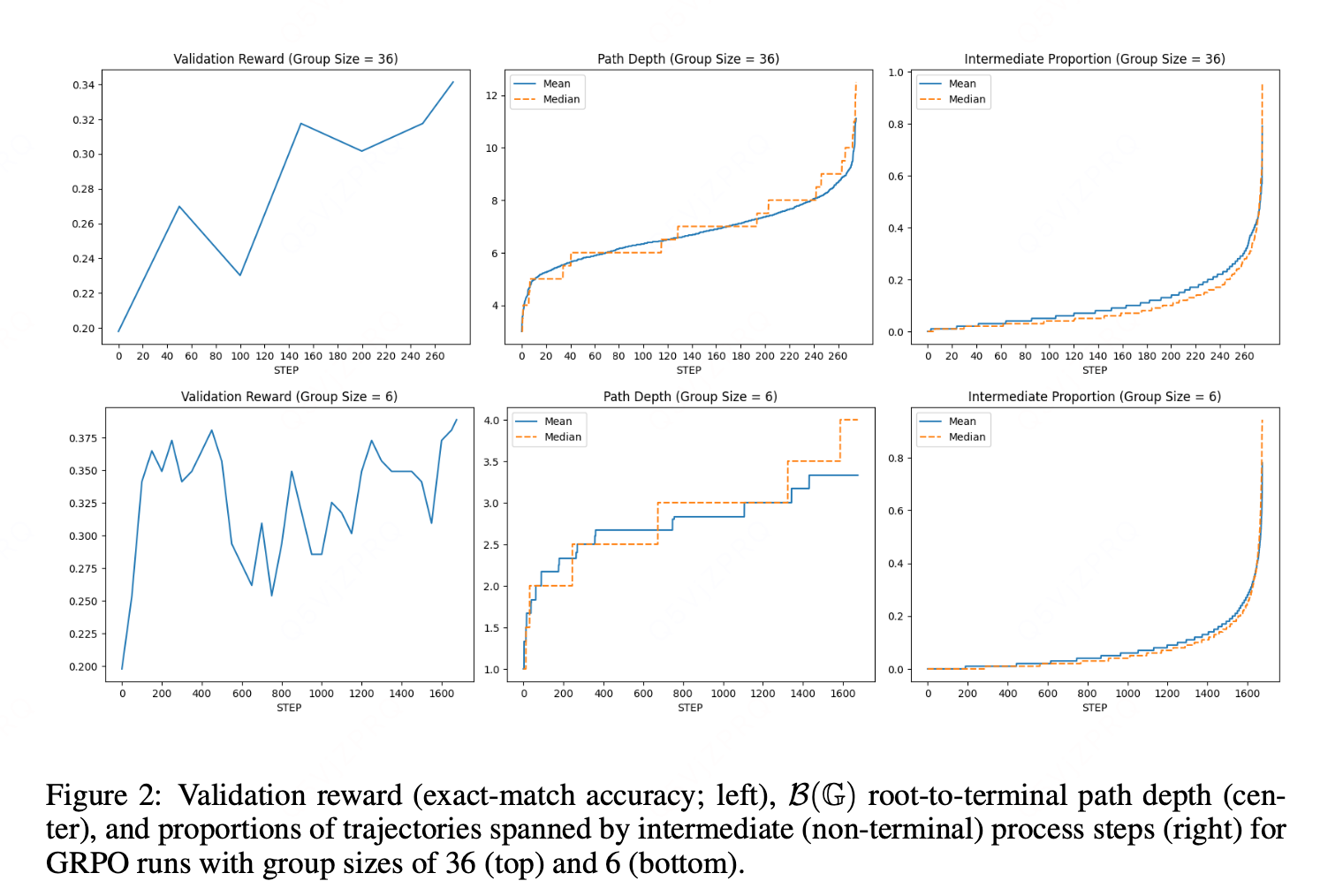
图 2 显示，对于组大小为 6 和 36 的两种情况，随着验证奖励趋于饱和，路径深度和中间比例均大幅提升。随着 GRPO 训练的推进，熵会急剧降低。这表明，当模型收敛到局部最优策略时，会产生越来越丰富的、能诱导 PRM 的结构。

1. 先明确指标与 "共享前缀" 的核心关联

路径深度：B (G) 树中根节点到终端节点的中间节点数，本质反映 "共享前缀的层级丰富度"------ 层级越多（比如先共享前 2 个令牌，再共享前 3 个令牌），路径越深。
中间比例：轨迹中属于 "中间过程步骤" 的令牌占比，本质反映 "共享前缀覆盖的令牌长度"------ 共享前缀越长，中间步骤覆盖的令牌越多，比例越高。

两者的共同驱动因素是：训练后期模型生成的轨迹，共享前缀越来越多、层级越来越深。

2. 验证奖励饱和 = 模型收敛到局部最优策略

验证奖励饱和意味着模型不再盲目探索，而是找到了 "能稳定拿到高奖励的有效路径"------ 此时模型生成的轨迹不再杂乱无章，而是聚焦于少数几条最优推理 / 生成路径。

这一点也得到了 Yu 等人（2025）的熵值结果支持：训练推进时熵急剧降低，熵越低说明轨迹的 "确定性越强"（不同轨迹之间的差异越小），越容易形成共享前缀。

3. 共享前缀的 "量" 和 "层级" 随收敛同步提升

初期训练（奖励未饱和）：模型还在探索不同路径，轨迹差异大，大多只有短而浅的共享前缀（比如仅前 1-2 个令牌相同），甚至没有共享前缀。此时路径深度浅（中间节点少），中间比例低（共享前缀覆盖的令牌少）。
后期训练（奖励饱和） ：模型收敛到最优路径后，绝大多数轨迹都会遵循 "相同的初始步骤→相似的中间步骤→不同的细节收尾" 模式。这会带来两个变化：
1. 共享前缀的 "长度变长"：比如从仅共享前 2 个令牌，变成共享前 5 个令牌，中间步骤覆盖的令牌数增多，导致中间比例提升；
2. 共享前缀的 "层级变深"：比如先有 "所有轨迹共享前 2 个令牌" 的上层过程集，再在其中分化出 "部分轨迹共享前 5 个令牌" 的下层过程集，中间节点增多，导致路径深度提升。

总结

验证奖励饱和的本质是模型 "找到并聚焦于有效路径"，轨迹从 "杂乱探索" 变成 "有序收敛"。这种收敛带来了更丰富的共享前缀结构（更长、层级更多），而路径深度和中间比例正是衡量这种结构丰富度的直接指标 ------ 因此两者会随奖励饱和大幅提升。

问题：需要遍历轨迹来计算吧？

参考：https://zhuanlan.zhihu.com/p/1955663865997157747

25-GRPO IS SECRETLY A PROCESS REWARD MODEL

GRPO 是"隐藏 PRM"

场景设定

步骤 1：构建过程集 B(G)（共享前缀的轨迹子集）

分析共享前缀：

步骤 2：确定每个过程集的起止点 s(λ) 和 e(λ)