【数据结构初阶】--从排序算法原理分析到代码实现操作，参透插入排序的奥秘！

🔥@晨非辰Tong： 个人主页
👀专栏：《C语言》、《数据结构与算法入门指南》
💪学习阶段：C语言、数据结构与算法初学者
⏳"人理解迭代，神理解递归。"

---

文章目录

• • 引言
  • 获取源码》点我！！《
• 一、排序的概念与运用
• • [1.1 什么是排序？](#1.1 什么是排序？)
  • [1.2 运用场景有哪些？](#1.2 运用场景有哪些？)
  • • [1.2.1 学生成绩排名](#1.2.1 学生成绩排名)
    • [1.2.2 视频平台热度排行榜](#1.2.2 视频平台热度排行榜)
  • [1.3 常见的排序算法](#1.3 常见的排序算法)
• 二、直接插入排序
• • [2.1 基本思想](#2.1 基本思想)
  • • [2.1.1 算法思路](#2.1.1 算法思路)
    • [2.1.2 特性总结](#2.1.2 特性总结)
  • [2.2 排序源码呈现](#2.2 排序源码呈现)
  • • [2.2.1 ==注意要点==](#2.2.1 ==注意要点==)
• 三、希尔排序
• • [3.1 基本思想](#3.1 基本思想)
  • • [3.1.1 算法思路](#3.1.1 算法思路)
    • [3.1.2 特性总结](#3.1.2 特性总结)
  • [3.2 排序源码呈现](#3.2 排序源码呈现)
  • • [3.2.1 ==注意要点==](#3.2.1 ==注意要点==)
• 四、谁才是插入排序家族的"效率之王"
• • 总结

---

引言

在排序算法的世界里，插入排序家族 看似简单，却暗藏效率之争。当朴素的直接插入排序，遇上剑走偏锋的希尔排序，==谁才是真正的性能王者？==本文将为您揭晓答案。

获取源码》点我！！《

---

一、排序的概念与运用

1.1 什么是排序？

排序：是将一组数据按照特定顺序重新排列的过程，通常是升序或降序排列。

1.2 运用场景有哪些？

排序在数据处理和展示中有着非常广泛的应用。比如下面这几个典型的场景：

1.2.1 学生成绩排名

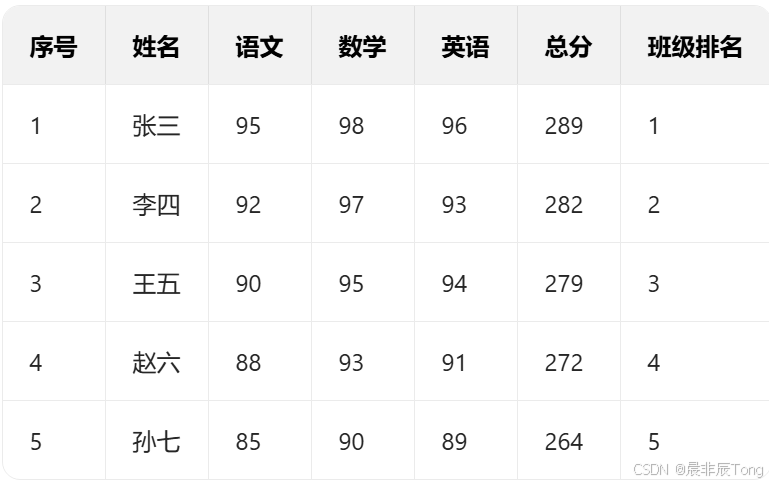
1.2.2 视频平台热度排行榜

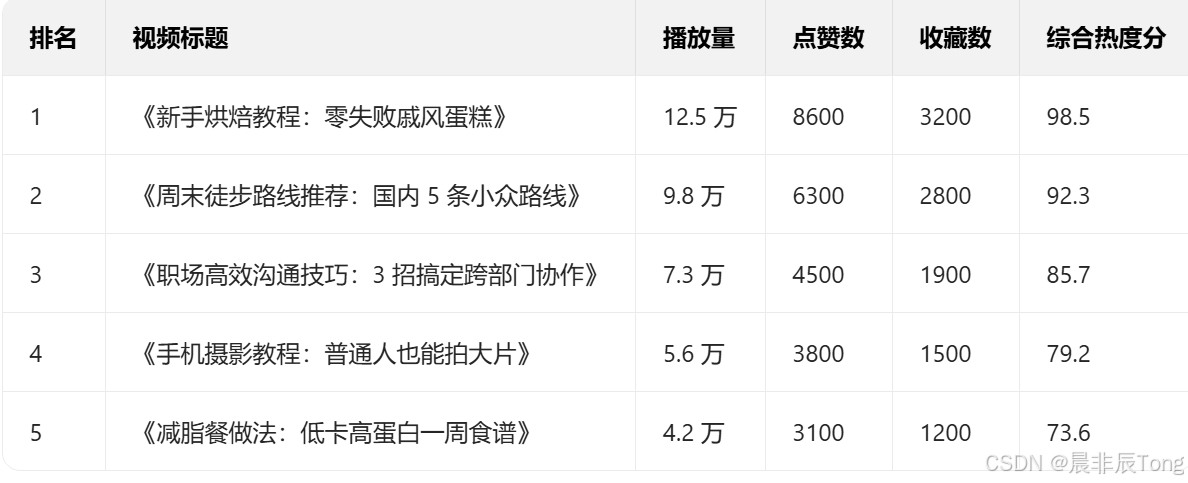
1.3 常见的排序算法

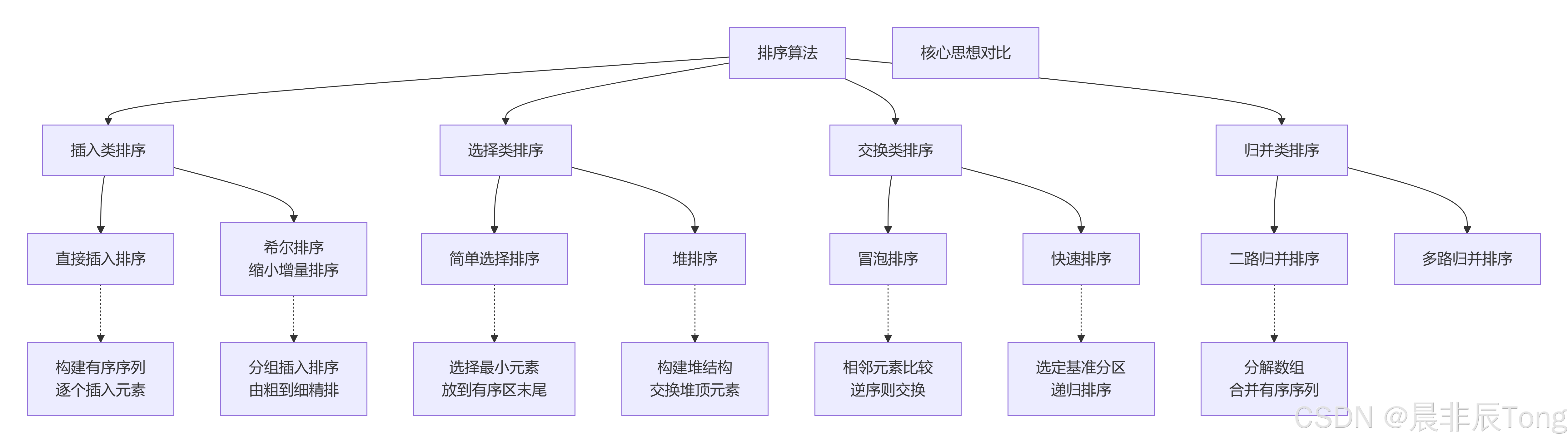
--下面先介绍插入排序的两种排序方法。

---

二、直接插入排序

2.1 基本思想

直接插入排序：是一种简单直观的排序算法，工作原理类似于我们整理扑克牌的方式：将未排序的元素按其关键码值的大小逐个插入到已排序序列的适当位置，直到所有的记录插入完为止，最后得到一个新的有序序列。

2.1.1 算法思路

首先，在一个乱序数组中，假设将变量 end 指向第一个元素当作有序（因为只有它自己，肯定是有序的），变量 temp 指向并保存未排序元素的第一位，基本方法就是将 end 与 temp 指向的元素进行比较。

简单的看第一次交换，从下标1开始，如果 arr[end] < temp ，那么二者就不用交换。end 一直比较到下标2的位置，这时 arr[end] > temp ，temp 先将1保存，随后 end-- 开始向前与temp比较寻找arr[end] < temp。

在end--过程中，若仍是 arr[end] > temp ，就 arr[end + 1] = arr[end] 。直到end-- < 0 结束比较（循环条件）， arr[end + 1] = temp 。当然，如果过程中 arr[end] < temp 就结束比较， arr[end + 1] = temp。

2.1.2 特性总结

• 元素集合越接近有序，直接插入排序算法时间效率越高；
• 时间复杂度：O(N²)；
• 空间复杂度：O(N)；

2.2 排序源码呈现

//Sort.c文件

//直接插入排序
void InsertSort(int* arr, int n)
{
	//外层循环：遍历整个数组（一直在尾部）
	for (int i = 0; i < n - 1; i++)
	{
		//变量追踪有序尾部
		int end = i;

		//变量存储第一个无序元素
		int temp = arr[end + 1];

		//内层循环：将有序与无序对比
		//升序排列；>  降序排列：< 
		while (end >= 0)
		{
			//比较end、temp
			//end大
			if (arr[end] > temp)
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else
			{
				break;
			}
		}

		arr[end + 1] = temp;
	}
}

//打印
void PrintArr(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

//------------------------------------------------------------------------------------------------------------------------------------------------//

//test.c文件
test01()
{
	int arr[] = {5,3,9,6,2,4};
	int n = sizeof(arr) / sizeof(arr[0]);
	PrintArr(arr, n);
	InsertSort(arr, n);
	PrintArr(arr, n);

}
int main()
{
	test01();
	return 0;
}

2.2.1 注意要点

- for (int i = 0; i < n - 1; i++)循环条件设置：

如图所示：外层循环主要是进行end的行为，因为end是追踪无序数列的尾部，当end到达下标为：n-1位置时，数列已经变成了有序，无需再比较。所以是i < n - 1.

---

三、希尔排序

3.1 基本思想

希尔排序：也称为缩小增量排序，是插入排序的一种高效的改进版本-->将整个 待排序的序列分割成若干个子序列 ，分别进行直接插入排序 ，待整个序列中的记录"基本有序"时，再对全体记录进行一次直接插入排序。

3.1.1 算法思路

• 初始化间隔：先选定⼀个初始间隔值 gap （通常n / 3 + 1）；
• 分组排序：把待排序所有记录按照 gap 进行分组，所有相距为 gap 的元素被划分到同一组，并对每⼀组内进行直接插入排序；
• 缩小间隔：然后 gap = gap / 3 + 1 得到下⼀个间隔，重新分组再进行插入排序，当 gap=1 时，就相当于直接插入排序。

3.1.2 特性总结

• 希尔排序是对直接插入排序的优化。
• 当 gap > 1 时都是预排序，目的是让数组更接近于有序。当 gap == 1 时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。
• 时间复杂度：不定，一般为O(N^1.3)
  

3.2 排序源码呈现

//Sort.c文件
//2)希尔排序
void ShellSort(int* arr, int n)
{
	int gap = n;
	while (gap > 1)
	{
		//取间隔
		gap = gap / 3 + 1;

		//分组循环	
		for (int i = 0; i < n - gap; i++)//i++比i+=gap少了一个循环
		{
			int end = i;
			//相同间隔的元素
			int tmp = arr[end + gap];
			//循环比较
			while (end >= 0)
			{
				if (arr[end] > tmp)
				{
					arr[end + gap] = arr[end];
					//不再是end--，为了同组比较内替换
					end -= gap;
				}
				else 
				{
					break;
				}
			}
			arr[end + gap] = tmp;
		}
	}
}

//------------------------------------------------------------------------------------------------------------------------------------------------//

//test.c文件
test01()
{
	int arr[] = {5,3,9,6,2,4};
	int n = sizeof(arr) / sizeof(arr[0]);
	printf("排序之前：");
	PrintArr(arr, n);
	//希尔排序
	ShellSort(arr, n);
	printf("排序之后：");
	PrintArr(arr, n);
}
int main()
{
	test01();
	return 0;
}

3.2.1 注意要点

• 为什么gap = n / 3 + 1?

  ：为了确保最后一次进行整体的直接插入排序，gap 最后必须为 1 ；

• 是分组插入，不是分别排序

  ：希尔排序是交替处理各个分组（i++），而不是完整排序一个分组后再处理下一个。

• 最后一轮必须是gap=1

  ：无论前面使用什么间隔序列，最后一遍必须是 gap=1 的标准插入排序

四、谁才是插入排序家族的"效率之王"

下面将从几个维度来比较直接插入排序、希尔排序，以此得出谁才是插入排序的效率之王！

对比维度	直接插入排序	希尔排序（缩小增量排序）
核心思想	将待排序元素逐个插入到已排序序列的合适位置，类似整理扑克牌的过程。	按增量将序列分割为多个子序列，对每个子序列进行直接插入排序，逐步缩小增量至 1（最终完成整体排序）。
时间复杂度	最佳：O (n)，平均：O (n²)，最坏：O (n²)（序列逆序）	最佳：O (n log n)，平均情况：O (n¹.³)（与增量选择相关）， 最坏：O (n²)（依赖增量序列）
空间复杂度	稳定（相等元素的相对位置不变）	不稳定（子序列排序可能破坏相等元素的相对位置）
优势	实现简单，对基本有序数据效率高	突破直接插入排序的 O (n²) 瓶颈，对无序数据的排序效率显著更高
劣势	对大规模无序数据效率极低（需频繁移动元素）	实现较复杂（需设计增量序列），增量选择对性能影响大，稳定性差

经综合对比考量：希尔排序凭借其 O(n^1.3) 的平均时间复杂度，在插入排序家族中稳坐"效率之王"的宝座，特别是在处理无序的中等规模数据时优势明显。

但直接插入排序在特定场景下（极小数据、基本有序、要求稳定）仍有其不可替代的价值，可视为"特定场景专家"。

---

总结

🍓 我是晨非辰Tong！若这篇技术干货帮你打通了学习中的卡点：
👀 【关注】跟我一起深耕技术领域，从基础到进阶，见证每一次成长
❤️ 【点赞】让优质内容被更多人看见，让知识传递更有力量
⭐ 【收藏】把核心知识点、实战技巧存好，需要时直接查、随时用
💬 【评论】分享你的经验或疑问（比如曾踩过的技术坑？），一起交流避坑
🗳️ 【投票】用你的选择助力社区内容方向，告诉大家哪个技术点最该重点拆解
技术之路难免有困惑，但同行的人会让前进更有方向～愿我们都能在自己专注的领域里，一步步靠近心中的技术目标！

结语：

算法世界犹如浩瀚星河，每一次对基础知识的深入探索，都像是点亮一颗新的星辰。直接插入排序与希尔排序的这场"兄弟之争"，让我们看到算法优化并非遥不可及------有时，一个巧妙的思路转变，就能带来性能的飞跃。

希尔排序虽以 "效率之王" 加冕，但直接插入排序在特定场景下的价值依然不可替代。这正印证了一个编程哲学：没有最好的算法，只有最合适的算法。掌握它们的本质差异，才能在未来的开发实践中做出最明智的选择。

希望这篇分析能让你对插入排序家族有了更立体的认识。别忘了在评论区留下你的看法：

➤ 实战中，你会更倾向于使用哪种算法？为什么？

➤ 你还想了解哪些排序算法的对比分析？

【下期预告】：当"直接选择"对阵"堆排序"，谁才是选择排序的终极赢家？我们下回分晓！