构建一个 DeepSeek 模型——通过键值缓存（Key-Value Cache, KV Cache）解决推理瓶颈

本章内容

自回归式 LLM 推理为何低效
解决方案：键值缓存（Key-Value Cache, KV Cache）及其代价
MQA 与 GQA：第一代缓解 KV Cache 内存压力的方案

要理解 DeepSeek 架构的关键创新，我们需要先看清这些创新要解决的技术痛点。本章对应全书开篇所述"四阶段路线图"的第 1 阶段：KV Cache 基础。它针对现代 LLM 推理中最根本的瓶颈。在进入第 2 阶段并理解 DeepSeek 的核心设计（如多头潜在注意力 MLA）之前，必须先掌握 KV Cache 的来龙去脉------以及它被设计出来要解决的问题。

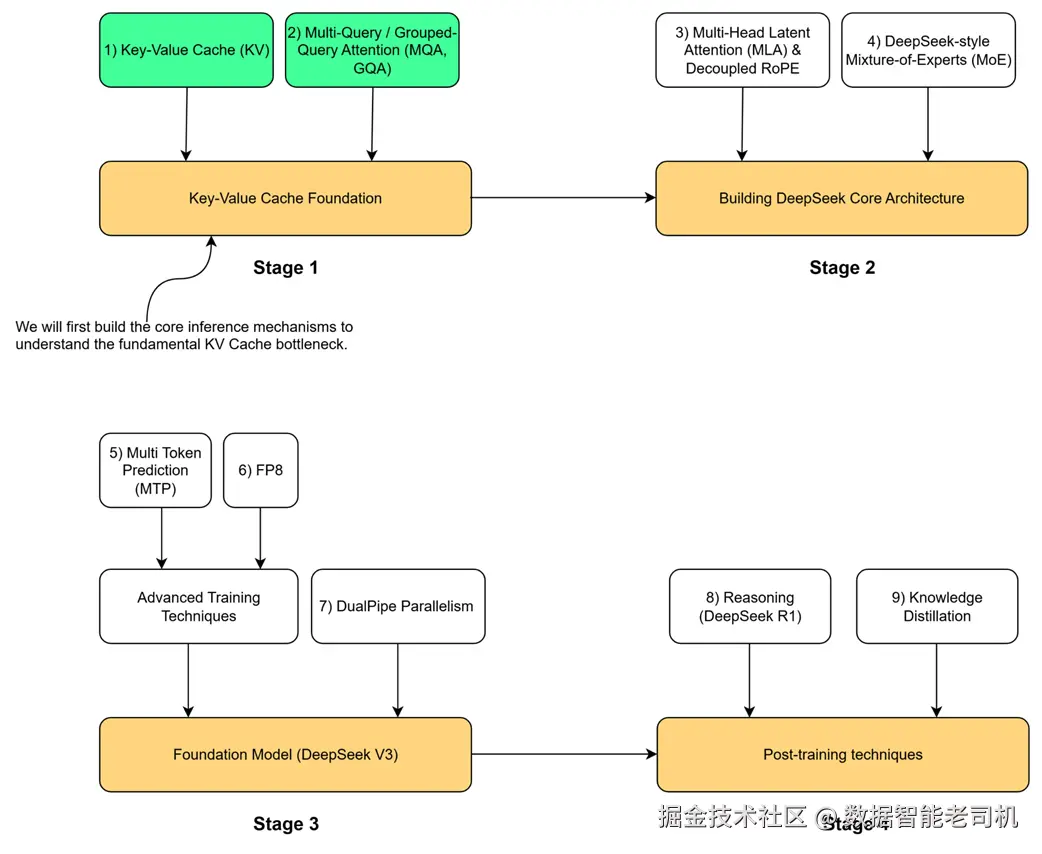
图 2.1　构建 DeepSeek 模型的四阶段路线图。本章将覆盖第 1 阶段的 KV Cache 基础。

如路线图所示，这一基础建立在两个核心概念之上：键值缓存（KV Cache） 及其第一代优化 多查询注意力（MQA） 和 分组查询注意力（GQA） 。这些技术是更先进架构的基石。第 2 阶段将引入 DeepSeek-V2 的核心创新：多头潜在注意力（MLA） 、解耦 RoPE 与 DeepSeek-Mixture-of-Experts（MoE） 。在深入这些之前，本章将分三步由浅入深，构建必要的理解：

先从零实现一个完整的自回归生成循环，可视化语言模型如何一次生成一个 token，从而直观看到传统路径的计算低效；
实现 KV Cache 本身。我们会用代码展示它带来的显著加速，同时揭示它的"暗面"：巨大的显存开销会引入新的严重瓶颈；
编写可运行的 PyTorch 层，实现 MQA 与 GQA 。它们是为缓解 KV Cache 内存问题而提出的第一代架构方案。务必认识到：这不是"免费午餐"------MQA/GQA 以模型质量与表征能力为代价换取内存效率与推理速度。其中 MQA 走向极致地节省内存，GQA 则在效率与效果之间做折中。通过亲手实现并权衡这些业界常见技术，我们才能为后续 DeepSeek 试图两全其美的独特创新做好铺垫。

2.1 LLM 推理循环：一次一个 token 的生成

首要概念：KV Cache 只在模型的"推理（inference）阶段"才相关。因此先区分 LLM 生命周期的两个阶段。

2.1.1 预训练 vs. 推理

训练（Training） ：耗资巨大、计算密集的学习阶段。模型在海量语料（万亿级 token）上学习语法、事实、推理模式与词间统计关系，并不断更新参数。训练完成后得到预训练模型，其参数被冻结。
推理（Inference） ：使用阶段。我们用固定参数的模型来完成任务------当你与聊天机器人对话，或调用 API 让模型"制定意大利旅行计划"时，就是在做推理。此时模型不再学习，只是在预测序列中的下一个 token。

本章讨论仅针对推理阶段：假设模型已训练完毕，我们的目标是高效地用它来生成文本。

2.1.2 自回归过程：不断追加 token 扩展上下文

在推理时，语言模型一次生成一个 token 。虽然前端 UI 可能让你觉得回复"一次性出现"，但底层是一个循序渐进 的过程，这就是自回归（autoregressive）生成。

核心思想：模型每次生成的新 token 立即被追加回输入序列，并成为下一步生成的上下文。这样形成一个反馈环，使模型能构造连贯且语境相关的文本。

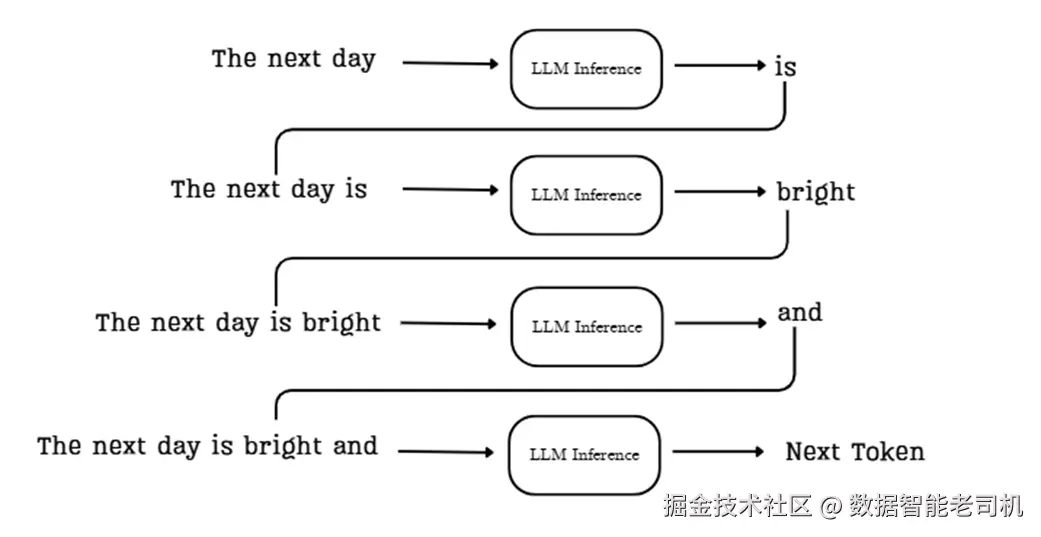
图 2.2　在自回归循环中，每一步的输出都会追加到下一步的输入中，使上下文逐步扩展。

让我们追踪图示流程，以"The next day."为例：

初始上下文：给模型一个起始提示，如 "The next day"。
第一次预测：将该序列送入 LLM 推理管线，预测下一个最可能的 token，例如 "is"。
追加并重复：将 "is" 追加到序列，下一步的输入变为 "The next day is"。
第二次预测：模型基于 "The next day is" 预测下一个 token，如 "bright"。
如此循环，直到生成特殊的序列结束标记或达到最大生成长度。

这种迭代、反馈驱动 的机制，是 Transformer 等自回归 LLM 构建连贯文本的根本。理解它，才能理解 KV Cache 在该范式下为何既必要又麻烦。

2.1.3 用 GPT-2 可视化自回归生成

下面的代码用预训练 GPT-2 演示自回归循环。它从一个起始提示开始，在循环中每次将当前整段序列 送入模型，取出最后一个位置 的预测 token，再把它拼回输入 ，进入下一轮。清晰可见：每生成一个新 token，都要做一次完整的前向计算。

完整代码与本书其他清单可在官方仓库获取：
github.com/VizuaraAI/D...

清单 2.1　用 GPT-2 可视化自回归生成

ini 复制代码

from transformers import GPT2LMHeadModel, GPT2Tokenizer
import torch

tokenizer = GPT2Tokenizer.from_pretrained("gpt2")
model = GPT2LMHeadModel.from_pretrained("gpt2")

prompt = "The next day is bright"
inputs = tokenizer(prompt, return_tensors="pt")
input_ids = inputs.input_ids

print(f"Prompt: '{prompt}'", end="")

for _ in range(20):
    outputs = model(input_ids)
    logits = outputs.logits

    next_token_logits = logits[:, -1, :]
    next_token_id = next_token_logits.argmax(dim=-1).unsqueeze(-1)

    input_ids = torch.cat([input_ids, next_token_id], dim=-1)

    new_token = tokenizer.decode(next_token_id[0])
    print(new_token, end="", flush=True)

print("\n")

运行后，初始提示后的文本会以逐 token的方式生成，例如：

'The next day is bright' and sunny, and the sun is shining. The sun is shining, and the moon is shining.

这个小例子强调了一个关键事实：每生成一个 token，都要"整段重算一次"模型 。你可以在循环体里看到 outputs = model(input_ids)；而 input_ids 是不断增长 的整个上下文序列，每一轮都重新送入模型。这自然引出一个关键问题：内部到底在算什么，这些计算是否都必须每次重复？

这正是引出 KV Cache 的入口。

2.2 核心任务：预测下一个 token

现在我们知道，LLM 为每个新 token 都会执行一次完整的计算前向。接下来我们剖开架构的层次，理解这一步包含了哪些计算。我们把聚焦点放在 Transformer 模块的"心脏"------多头注意力（Multi-Head Attention） 。模型正是在这里判断各个 token 之间的关系。

下面这张示意图给出了整体路线图。它展示了我们的示例 "The next day is bright" 如何流经后续要分解的关键部件。请记住这幅图，它代表了我们接下来要搭建的完整过程。

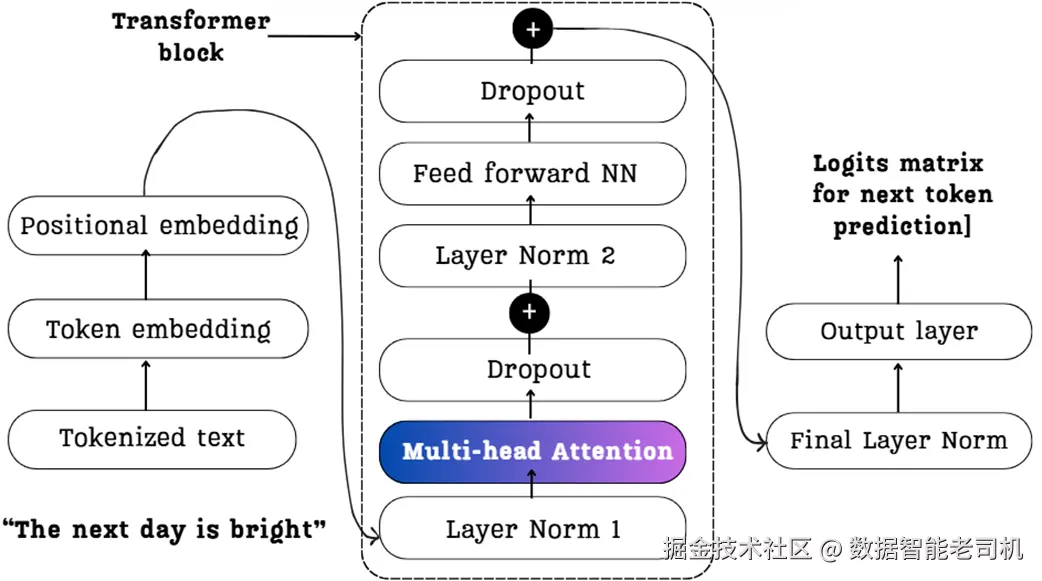
图 2.3　Transformer 模块架构的高层概览。图中展示了从初始输入 token（"The next day is bright"）到嵌入、再到多头注意力与前馈网络，最终得到用于"下一个 token 预测"的 logits 的完整数据流。

2.2.1 从输入嵌入到上下文向量：一次数学化的走查

图 2.3 给出了主要部件，但为了理解推理时会被重复哪些计算，我们需要进一步放大最关键的组件：多头注意力块。模型在这里计算 token 间的关系，并产出富含语境信息的"上下文向量（context vectors）"，它们构成了模型理解的基础。

让我们将输入序列 "The next day is" 通过一次注意力计算，看看底层究竟做了什么。

步骤 1：将输入投影为 Query、Key、Value

经过分词与嵌入之后，我们用矩阵 X 表示输入。为了易于讲解，先用小维度：假设 X 形状为 (4, 8)，表示 4 个 token、每个 8 维嵌入。真实模型中这个维度要大得多（例如 DeepSeek-V2 为 5120，DeepSeek-V3 为 7168），但数学原理相同。

注意力块的第一步，是把 X 分别线性映射成三种表征：Q（Query） 、K（Key） 、V（Value） 。做法是将 X 分别与三组可训练权重 Wq/Wk/Wv 相乘。

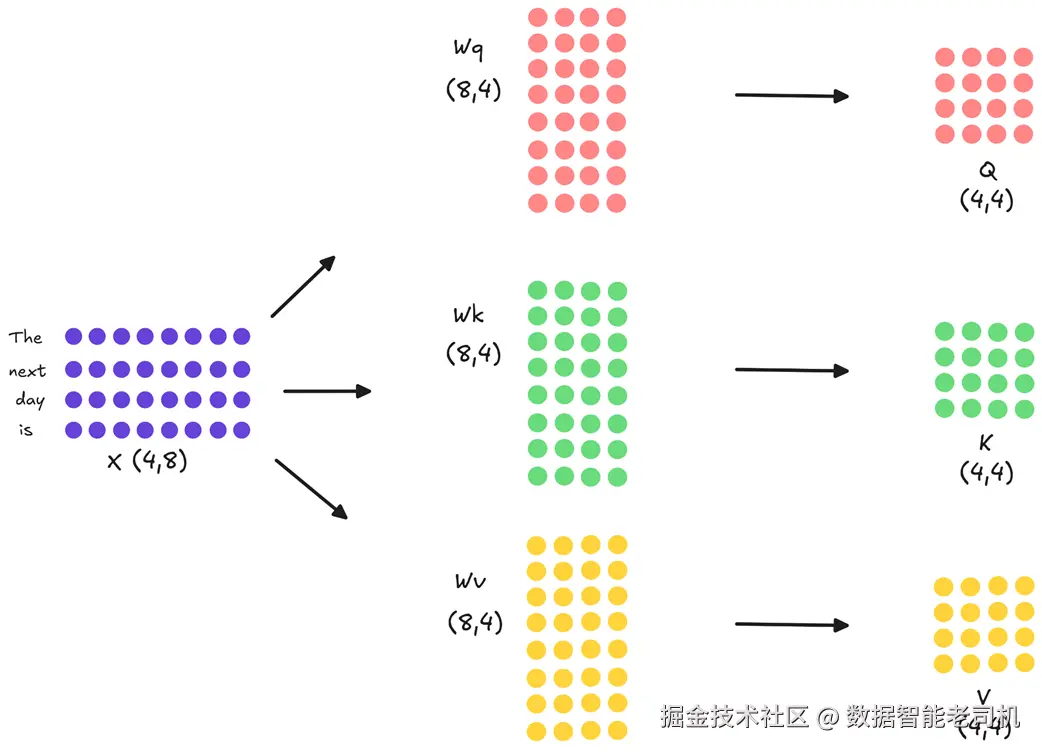
图 2.4　输入嵌入矩阵 X 被投影为 Q、K、V 三个矩阵。每个投影都是与一套独立可学习权重做矩阵乘法。

如图所示：

X (4×8) × Wq (8×4) → Q (4×4)
X (4×8) × Wk (8×4) → K (4×4)
X (4×8) × Wv (8×4) → V (4×4)

三者代表输入 token 的不同"角色"：Q 表达"我要找什么"，K/V 表达"我能提供什么"。

步骤 2：计算注意力分数

接着需要判断每个 token 与其他 token 的相关性。做法是用 Q 去乘以 K 的转置（Kᵀ）。

图 2.5　Q 与 Kᵀ 的点积得到注意力分数矩阵。该矩阵的每个元素都代表一个 token 对另一个 token 的相关程度。

得到的注意力分数矩阵形状为 (4×4)，量化了任意 token 对之间的关系。例如第 4 行第 2 列表示 token "is" 应该在多大程度上关注 token "next"。

步骤 3：从分数到上下文向量

这些原始分数接着会被进一步处理：先做缩放（稳定训练），再应用因果掩码 （保证只能关注到当前位置之前的 token，防止"偷看未来"），即把分数矩阵的上三角置零。最后对每一行做 softmax ，将分数转为注意力权重（概率分布，逐行和为 1）。

然后用这些注意力权重去乘以 V。

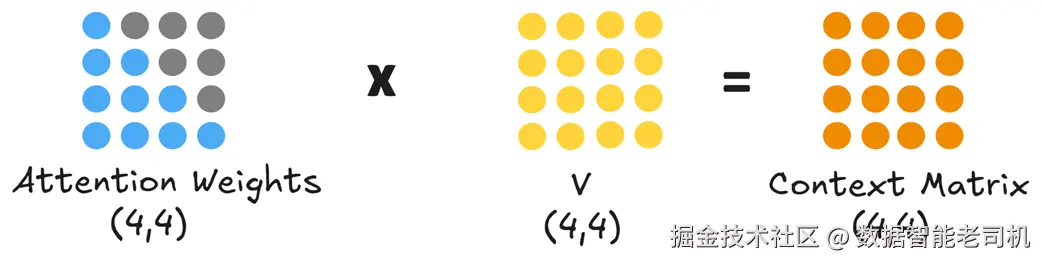
图 2.6　注意力权重与 Value 相乘生成最终的上下文矩阵 。此时每一行都是对原始 token 的语境增强表示。

这一步得到的上下文矩阵形状仍为 (4×4)。例如 "is" 的上下文向量就是对其之前所有 Value 向量的加权和，聚合了整段前文的重要信息。

步骤 4：扩展到多头注意力

以上描述是单头注意力。但模型往往需要同时捕捉多种关系：比如句法依赖（主谓一致）与语义关系（词义）。单一注意力可能难以兼顾。

于是引入多头注意力：不是用一套大投影，而是用多套更小、彼此独立的投影矩阵（每个"头"一套）。

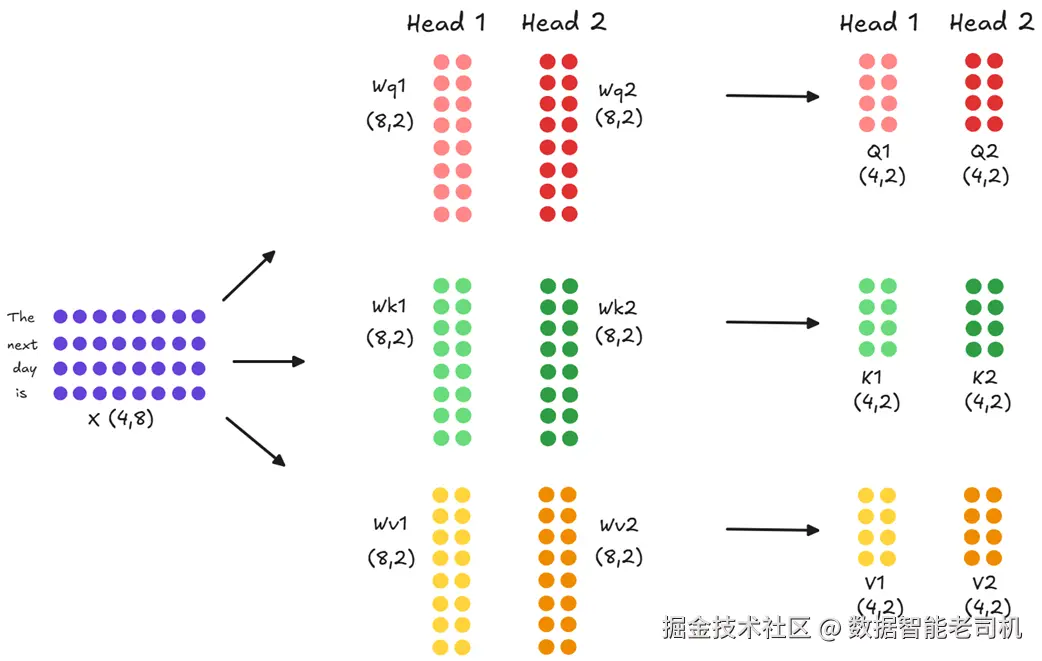
图 2.7　多头注意力中的并行投影。输入嵌入 X 会被并行地映射成每个注意力头各自的 Q、K、V。

如图所示，若有两个注意力头，原本 (4,8) 的输入不会映射成三份 (4,4)，而是并行映射成六个 (4,2)：Q₁/K₁/V₁（头 1），Q₂/K₂/V₂（头 2）。

然后每个头独立并行地计算自己的注意力分数：头 1 用 Q₁ 与 K₁，头 2 用 Q₂ 与 K₂。

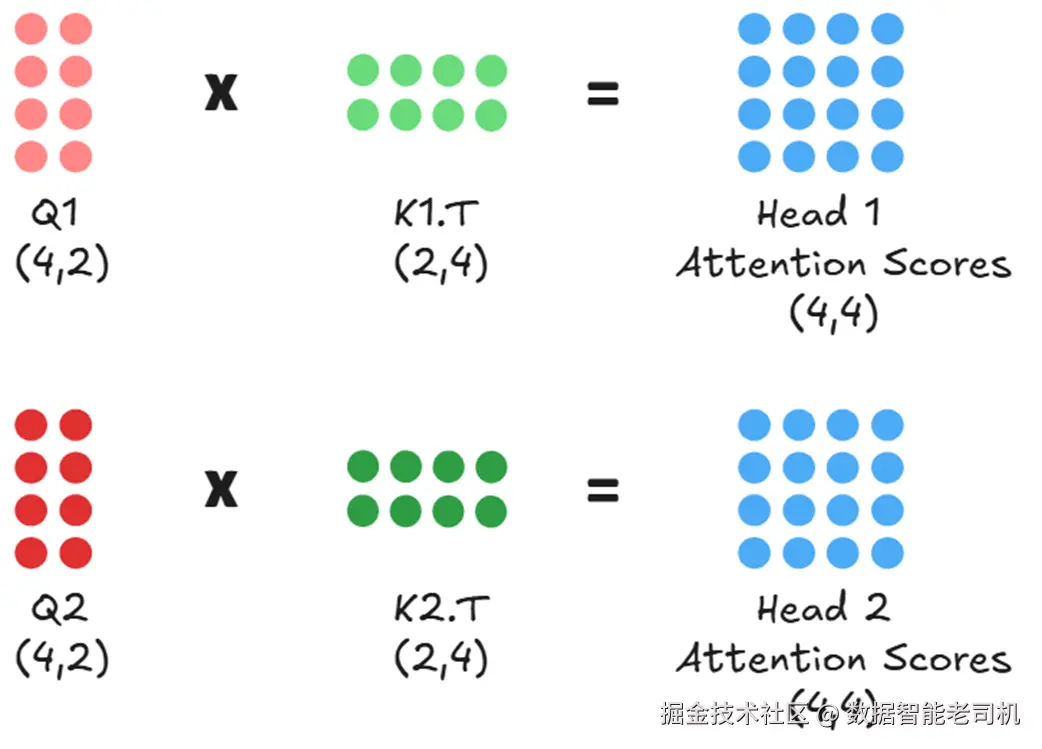
图 2.8　每个注意力头都会独立得到自己的注意力分数矩阵。

多头注意力的威力在于：每个头都在不同的表征子空间审视同一个输入。各头的投影矩阵不同，因此它们学到的关注点也不同：头 1 也许更偏语法，头 2 更偏语义，等等。

对每个头得到的原始分数，还需分别做缩放、掩码、softmax，得到每个头自己的注意力权重：

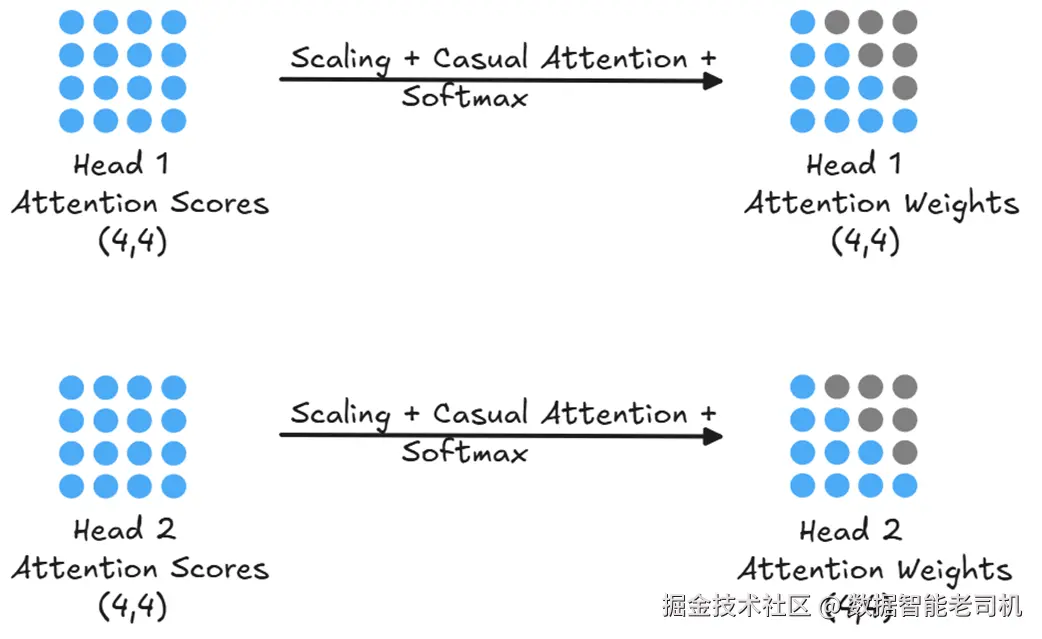
图 2.9　各头的注意力分数会各自完成缩放、掩码与 softmax，得到最终的注意力权重。

有了每个头的注意力权重，就可以与各自的 V 相乘，得到各头的上下文矩阵：

图 2.10　每个头产出自己的上下文矩阵，代表它对输入序列的特定"语境视角"。

此时我们拥有两个 (4,2) 的上下文矩阵：头 1 的与头 2 的。下一步要把这些并行信息合并起来供后续层使用，分两步走：

拼接（concatenate） ：把所有头的上下文矩阵在最后一维（列）上拼接。

图 2.11　将各头上下文矩阵拼接成一个更丰富的矩阵，再送入最终的输出投影层。

把两个 (4,2) 拼接成 (4,4)，聚合了两头的洞见。

输出投影（output projection） ：拼接后的矩阵再过一层线性变换，把多头信息"混合"并投回主模型期望的维度，得到多头注意力块的最终上下文矩阵（此例仍为 4×4）。

这种并行-多视角-再统一的流程，赋予了 Transformer 强大的表达能力。这个上下文矩阵将传给后续层，最终产出用于下一个 token 预测的 logits。

2.2.2 从上下文向量到 logits

我们已经看到注意力机制如何处理输入嵌入并产出增强的上下文矩阵。对 "The next day is" 而言，这是一个 (4,4) 的矩阵，每行对应一个 token 的新语境向量。

接下来，这个矩阵会继续通过 Transformer 模块的后续层，最终得到用于预测下一个 token 的 logits。

步骤 1：前馈网络（FFN）

上下文矩阵先进入当前 Transformer 块内的 FFN 。与注意力"跨 token 聚合"不同，FFN 对每个 token 的上下文向量逐 token、独立地做非线性变换（通常是两层线性层与中间激活）。FFN 的输出形状与输入保持一致（仍是 4×4），便于残差相加。

步骤 2：穿越多个 Transformer 块

FFN 的输出不会直接出块，而是经过层归一化、残差连接等操作构成一个完整的 Transformer 块 的输出；然后作为输入喂给下一层块。这个流程会按模型深度重复（例如 GPT-2 small 为 12 层）。

步骤 3：最终投影为 logits

当序列穿过最顶层 Transformer 块后，最终的上下文矩阵会再经过一次层归一化，然后进入最终输出层做预测。

这里引入一个术语：logits 。
定义：什么是 Logit？　logit 是未归一化的分数。对序列中的任一位置，模型会为词表中的每一个词产出一个 logit。某个词的 logit 越大，就越可能是"下一个 token"。

最终输出层是一个线性层，它将最终的上下文矩阵投影到词表维度 ，得到 logits 矩阵。

图 2.12　从最终上下文矩阵到 logits 矩阵。输出层把每个上下文向量映射为一条很长的分数向量（词表大小个分量）。

如图所示：

输入：来自最顶层块的最终上下文矩阵（例：4×4）。
变换：输出层把每一行映射成长度为 50,257 的向量（GPT-2 的词表大小）。
输出：形状为 (4, 50257) 的 logits 矩阵。

矩阵的每一行，都是"某个位置之后该选哪个词"的全词表打分：第一行对应"The"之后的预测，第二行对应"next"之后，依此类推。

现在我们有了原始分数矩阵，模型如何做出唯一的下一个 token 选择？下一步包含了优化推理流程的关键洞见。

2.2.3 关键洞见：为何只有"最后一行"有用

我们得到的 logits 矩阵形状为 (4, 50257)，它包含了输入序列中每个位置 的预测。但我们的目标非常明确：仅需预测完整输入 "The next day is" 之后的那个 token。

这意味着：矩阵里绝大多数行都可以丢弃。

第 1 行（"The" 之后预测）无关；
第 2 行（"next" 之后）无关；
第 3 行（"day" 之后）无关；
只有最后一行，即对应 "is" 的 logits，才是我们真正需要的。这条向量决定了下一个 token。

这就是关键洞见：既然我们每次只用最后一行 来做决策，却在每一步都把前面所有行重新算一遍 ，那就是巨大的浪费。这个观察正是 KV Cache 以及它的衍生方案 MQA/GQA 的根本动机。

图 2.13　最终的预测步骤。将"最后一行 logits"转为概率分布，并选择概率最高的 token 作为输出。

选择下一个 token 的步骤为：

取最后一行 logits：从 (4, 50257) 中只保留最后一行，得到形状 (1, 50257) 的向量；
softmax：把该向量转为概率分布（各值在 0--1 且和为 1）；
argmax：取概率最大的索引，它对应词表中的某个 token；若是 "bright"，则这一步的输出就是 "bright"。

这个从原始文本到单个预测 token 的流程，会对每个生成的 token 重复一次。请牢记：最终的决策只依赖最后一个 token 的上下文向量 。而这个向量之所以"足够"，是因为自注意力已经把此前所有 token 的信息以加权方式聚合进来了。

这自然引发怀疑：既然我们不断把越来越长的序列"整段"喂回模型，注意力块里是不是做了大量不必要的重复计算 ？下一节我们会用数学方式证明：答案是肯定的。

2.3 重复计算的问题

到目前为止，我们已经确立了两个关于 LLM 推理的关键事实：

模型在自回归循环中一次生成一个 token，并把自己的输出再喂回作为输入。
为了预测下一个 token，模型实际上只需要当前序列最后一个 token 的上下文向量。

现在把这两个想法联系起来：如果模型不断地对一条不断变长的序列做完整处理，而做决策时却只用到最后一个 token 的信息，那就意味着有大量计算可能是不必要的。直觉上看，我们似乎在一遍遍地重复算同样的东西。

下面我会展示：在推理阶段，我们的确重复了许多计算。随后我们会看到如何避免这些重复，这将把我们直接引向 KV Cache 的概念。

2.3.1 直觉：我们是不是在反复计算同一件事？

让我们把直觉变成更具体的数学论证。先通过逐步追踪每步的数据流来直观展示冗余，再通过计算复杂度来量化它的性能影响。我们回到图 2.2 的自回归循环，但这次关注每一步传入模型的数据。

假设起始提示为 "The next day."

推理第 1 步：

输入："The next day"
过程：三个 token 经过整个 LLM 流水线
输出："is"

推理第 2 步：

新 token 追加到末尾
输入："The next day is"
过程：这四个 token 再次经过整个流水线
输出："bright"

推理第 3 步：

又追加新 token
输入："The next day is bright"
过程：这五个 token 再次经过整个流水线
输出："and"

注意这个模式：在第 2 步里，我们又重新处理 了 "The"、"next"、"day" 这些 token------它们在第 1 步已经处理过了。第 3 步里，我们又重算了 "The"、"next"、"day"、"is"。也就是说，我们为了在末尾多加一个新 token，不断把同样的一段旧上下文反复送进整个架构里重算。

这显然低效------就像你每次想读第 n 章之前，都从第 1 章把书重读一遍。如果每章花费固定时间，那么读到第 n 章的工作量就是 1+2+...+n，呈**二次（O(n²)）**增长。

这种重复计算的主要弊端是成本呈爆炸式增长：每多一个 token，GPU 就要重新处理并存储越来越多的数据，使时间与内存占用随序列长度迅速增长。

这种"我们在重复干活"的直觉是正确的 。接下来用一个手把手 的例子，用数学方式 证明：在每一步推理中，我们确实在注意力机制里重复计算了完全相同的结果。

2.3.2 数学证明：把重复计算"画"出来

直觉告诉我们在做冗余工作。现在通过对比相邻两步推理中的注意力计算，我们会"亲眼"看到有多少值被重复计算了。

步骤 A：时刻 T=4 的推理（输入："The next day is"）

考虑模型刚处理完输入 "The next day is"，准备预测下一个 token。这是一条包含 4 个 token 的序列。图 2.14 展示了该序列在单个注意力头中的一次完整计算。

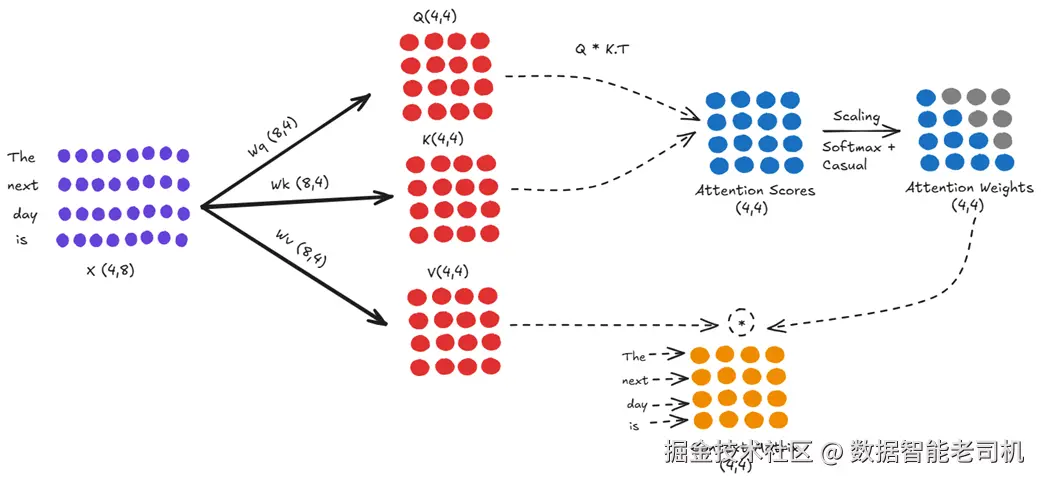
图 2.14　输入序列 "The next day is" 的完整注意力计算。

逐步跟踪图 2.14 的数据流：

输入嵌入 X：左侧是形状 (4, 8) 的输入嵌入矩阵 X（四个 token、每个 8 维）。
投影：X 依次与固定的、已训练好的权重矩阵 Wq、Wk、Wv 相乘，得到 Q/K/V，此例形状均为 (4, 4)。
注意力分数 ：用 Q × Kᵀ 得到 (4, 4) 的注意力分数矩阵。
注意力权重 ：对分数矩阵做缩放、因果掩码并 softmax，得到 (4, 4) 的注意力权重矩阵（未来位置被掩蔽为 0）。
上下文矩阵 ：注意力权重再与 V 相乘，得到 (4, 4) 的上下文矩阵。

随后，上下文矩阵继续穿过 Transformer 其余结构。正如我们已说明的，只有最后一行 （对应 "is" 的上下文向量）会被用于生成最终 logits 并预测下一个 token。假设此时模型正确地预测出 "bright"。

步骤 B：时刻 T=5 的推理（输入："The next day is bright"）

按照自回归循环，新预测的 "bright" 会被追加到序列末尾。新输入是包含 5 个 token 的 "The next day is bright"。这条更长的序列再次进入完全相同 的注意力机制，并使用同一组已学习权重（Wq/Wk/Wv）。

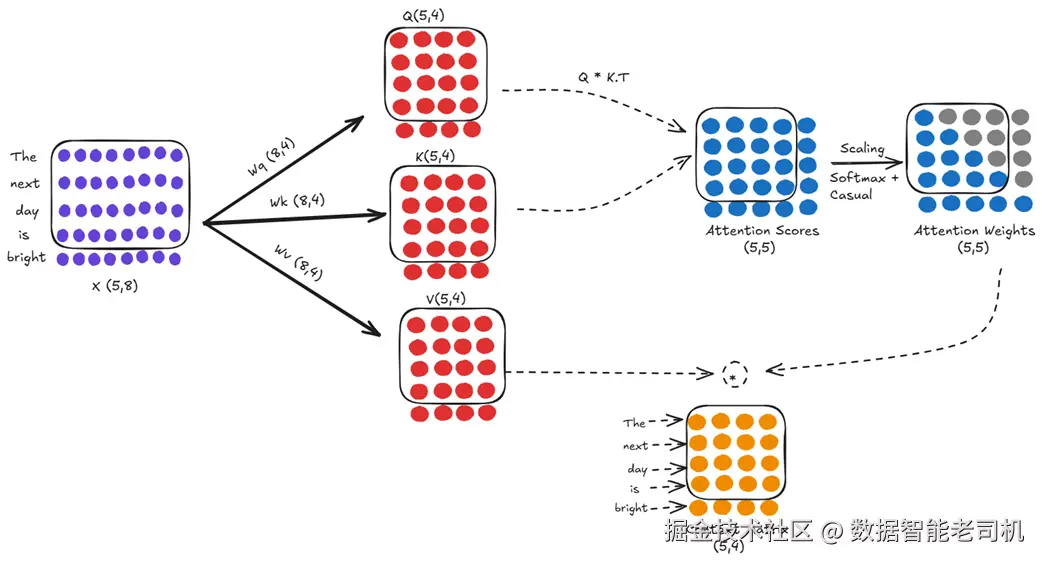
图 2.15　对新的 5-token 输入做完整注意力计算。

表面上看，这是一轮全新的计算。但把它和刚才那一轮对比就会发现关键点：

新的输入矩阵 X（5×8）前四行 与上一步的 X（4×8）完全相同；
由于推理时权重（Wq/Wk/Wv）是固定的，因此新的 Q/K/V（5×4）前四行 也分别与上一步的 Q/K/V（4×4）完全相同；
这会直接级联到注意力分数计算：任意位置 (i, j) 的分数是第 i 个 query 与第 j 个 key 的点积。因为前四个 query 与前四个 key 与上一步完全一致，所以新 (5×5) 分数矩阵的左上 (4×4) 子块 与上一步的 (4×4) 分数矩阵一模一样。

也就是说，我们在每一步 都对整段历史 重做了投影与注意力分数计算。计算资源被大量浪费。而最低效的是：做完所有这些老历史的重复计算后，我们最终用于预测的，却只是新增 token（"bright"）的那一行上下文向量。

为了多算一行，我们把整段历史又算了一遍，然后还把旧行的大部分结果丢掉。这正是推理优化必须解决的核心问题。

2.3.3 性能影响：把复杂度从二次降到一次

上述冗余不仅在理论上低效，对性能也有严重影响，尤其当输入序列变长时。理解这一点的最佳方式是看计算复杂度。

说明：这里讨论严格限定在**推理（inference）**阶段。

在没有任何优化时，注意力机制的核心成本随序列长度 n 呈二次增长。对每一层、每个注意力头，计算注意力分数所需的工作量是 O(n²)。虽然还会乘上层数 L 和头数 H 等常数，但主导因素是相对于 n 的二次关系。

为什么是二次？想想注意力分数矩阵：

4 个 token → 计算一个 4×4 的矩阵（16 个分数）；
5 个 token → 5×5（25 个分数）；
1000 个 token → 1000×1000（100 万个分数）。

在自回归生成的每一步，我们都要重新算这一整块 n×n 的矩阵，即反复做 O(n²) 的工作。随着 n 变大，计算量爆炸式增长。二次复杂度是导致未缓存推理在长序列上代价高、速度慢的主因------越到后面的 token，生成就越慢，因为需要重算的历史越多。

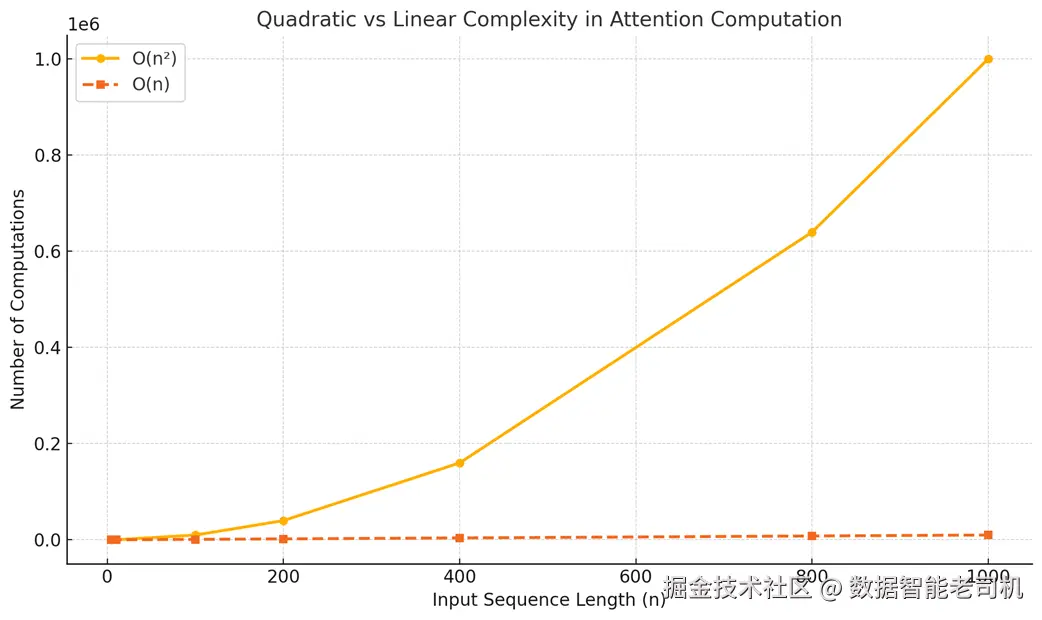
图 2.16　未缓存自回归推理的二次（O(n²)）增长 vs. 理想的一次（O(n)）增长的对比示意。

推理优化的目标，就是把这种二次过程变成一次（O(n)） 。在一次复杂度下，生成新 token 的计算量随序列长度呈线性增长，而不是平方增长。也就是说，长序列上生成新 token 的确更慢一些，但增长趋势温和得多：把上下文长度翻倍，计算量大致也只翻倍，而不是翻四倍，从而避免"爆炸"。

缓存（caching）恰好能达成这一点：把过去计算的结果存起来 ，而不是每次重算。正如上面的可视化所示，新 token 到来时，只需计算与它相关的新部分；历史部分直接从内存取回。

这种从二次到一次的转变，是缓存之所以不只是"优化"，而是让大上下文 LLM 推理可用的基础性要求。这也解释了我们将用代码演示的显著加速：

无缓存（O(n²)） ：生成第 100 个 token 远慢于第 10 个；
有缓存（O(n)） ：生成第 100 个 token 与第 10 个 token 所需时间大致同量级。

既然已经明确了需求之迫切，我们就可以开始构建解决方案 了。接下来就进入 KV Cache。

2.4 解决方案：用缓存提升效率

解决这个问题的方法既优雅又直观：如果我们在反复计算同样的值，为什么不只算一次 ，然后把结果存起来复用？这就是"缓存"的核心思想。

通过保存以往的计算结果，我们可以避免对已见过的 token 重新计算。这样就能摆脱二次复杂度的陷阱，把计算时间降到更高效的线性量级。这一强大的优化被称为键---值缓存（Key-Value Cache，简称 KV Cache） 。

2.4.1 缓存什么？一步步推导

要理解需要缓存什么，我们必须从最终目标反推。正如 2.2.3 节所述，在每一步推理中，我们的目标只是得到最近那个 token 的上下文向量。

继续我们的例子：模型刚处理完 "The next day is"，并生成了 "bright"。现在的新输入序列长度为 5。为了预测下一个 token，我们只需要 "bright" 的上下文向量。

图中的方框值来自前面的步骤。由于这些值在不同步之间保持不变，我们将它们缓存起来。此节后续图片遵循同样原则。

图 2.17　在整个上下文矩阵中，只有最后一行（对应最新 token）的向量，是预测下一个 token 所必需的。

所以，我们的直接目标是算出这一行向量 。让我们倒推，找出生成它所需的最小计算集合。

"bright"的上下文向量如何得到？

根据前面对注意力机制的回顾，上下文向量 来源于注意力权重 与 Value 矩阵的相乘。既然只需要 "bright" 的那一行上下文，我们只需计算该行对应的乘法。

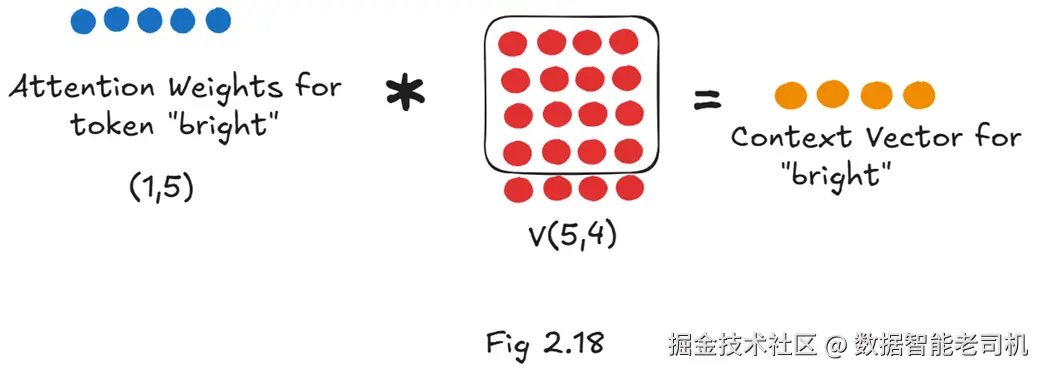
图 2.18　"bright"的上下文向量 = 该 token 的注意力权重（1×5）× 全部 Value 矩阵（5×4）。

如图 2.18，要得到目标向量，我们需要两样东西：

"bright"的注意力权重：一个 1×5 的行向量，表示 "bright" 对序列中每个 token（含自身）的关注程度；
完整的 Value 矩阵（5×4）：包含序列中每个 token 的"内容"表示。

继续倒推： "bright"的注意力权重如何得到？

注意力权重来自对注意力分数 做 softmax。要拿到 "bright" 的注意力分数，就需要把它的 Query 向量 与完整的 Key 矩阵的转置做点积。

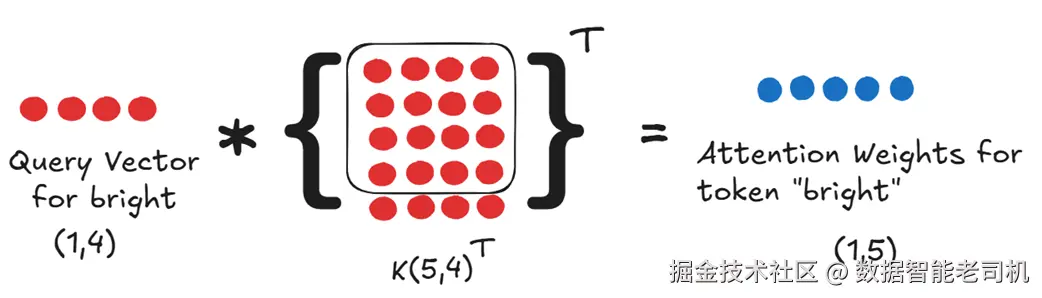
图 2.19　"bright"的注意力权重由其 Query 向量与全序列的 Key 向量共同决定。

因此，本质上我们需要：

新 token 的 Query 向量；
完整的 Key 矩阵（序列中所有 token 的 Key）。

到此为止，为了得到 "bright" 的上下文向量，我们需要：

"bright"的 Query（q_bright）
完整的 Key 矩阵（K）
完整的 Value 矩阵（V）

接着追根溯源：这些 Q/K/V 向量是怎么来的？

它们都是把输入嵌入通过训练好的权重矩阵 Wq/Wk/Wv 投影得到的。这里可以区分新增与历史两部分。

当新 token "bright" 到来时，我们必须为它计算自己的 Q/K/V------也就是用它的输入嵌入 X_bright 分别乘以 Wq/Wk/Wv 三个矩阵。

图 2.20　新 token 仅需三次必要的投影：把 "bright" 的嵌入各自投影为 Q、K、V。

如图 2.20 所示，新增所需的投影只有这三次：

计算 "bright" 的 Query；
计算 "bright" 的 Key；
计算 "bright" 的 Value。

现在终于可以回答关键问题：序列里历史 token（"The"、"next"、"day"、"is"）的 Key/Value 怎么办？

在 2.3 节的低效方案里，我们会从头再算一遍。但现在我们知道这是浪费------这些历史 token 的 Key/Value 在先前推理步骤里已经算过 ，而且不会改变。

这就是缓存登场的地方：与其重算，不如把前一步得到的 Key/Value 矩阵 保存在内存中------它们构成了 KV Cache 。于是形成如下高效流程，也解释了为什么只缓存 K/V 而不缓存 Q：

新 token 的计算：当 "bright" 到来，为它做图 2.20 中的三次投影，得到它的 Q/K/V；
组装完整的 K/V 矩阵：
- 从 Key Cache 取出 "The next day is" 的 4×4 Key 矩阵；
- 把 "bright" 的新 Key 向量追加上去，得到新的 5×4 Key 矩阵；
- 对 Value 做同样操作，得到 5×4 Value 矩阵；
计算注意力 ：用 "bright" 的新 Query 与更新后的 K/V 做注意力计算，得到所需的单行上下文向量；
更新缓存：把新的 5×4 Key/Value 矩阵写回缓存，准备下一步。

这就是 KV Cache 的本质：每一步只为新增 token 付出那三次投影的代价；历史信息全部由缓存提供。我们不缓存 Query ，因为每一步只需要当前 token 的 Query，它必须现算。正是这套"只缓存 K/V"的简单而强力的技巧，把注意力计算从极慢的二次复杂度 变成高效的一次复杂度。

2.4.2 带 KV 缓存的全新推理循环

明确了要缓存什么之后，我们可以给出新的高效自回归生成流程。每一步都不再重算整段历史，而是复用缓存的 K/V：

接收新 token：拿到该 token 的嵌入；
计算新投影：仅为这个新 token 计算 Q/K/V 三个向量；
从缓存读取 ：取出所有历史 token 的 Key/Value 矩阵；
追加到缓存：把新 token 的 K/V 追加到缓存矩阵末尾，得到更新后的完整 K/V；
计算注意力 ：用新 Query 与更新后的 K 计算分数并 softmax 成权重；
算上下文向量 ：注意力权重 × 更新后的 V → 得到新 token 的上下文向量；
预测下一个 token：把该向量送入后续层，得到 logits 并采样/取 argmax；
更新缓存 ：把扩展后的 K/V 写回缓存，进入下一轮。

这样就避免了朴素方案中的大量冗余。需要强调的是，缓存是逐层、逐头维护的：模型的每个 Transformer 层、每个注意力头都有自己的 K/V 缓存，以保留每层所学习到的特化上下文。

2.4.3 KV 缓存的提速实证

从理论上把复杂度从二次降到一次已经很清楚，而在实践中效果更直观。我们可以用 Hugging Face 的预训练 GPT-2 做一个小测试：开启与关闭 KV 缓存（use_cache） ，分别生成 100 个新 token，并计时。

代码清单 2.2　演示 KV 缓存的加速效果

ini 复制代码

prompt = "The next day is bright"
inputs = tokenizer(prompt, return_tensors="pt")
input_ids = inputs.input_ids
attention_mask = inputs.attention_mask

# Timing without KV cache
start_time_without_cache = time.time()
output_without_cache = model.generate(
    input_ids,
    max_new_tokens=100,
    use_cache=False,               # A
    attention_mask=attention_mask
)
end_time_without_cache = time.time()
duration_without_cache = end_time_without_cache - start_time_without_cache
print(f"Time without KV Cache: {duration_without_cache:.4f} seconds")

# Timing with KV cache
start_time_with_cache = time.time()
output_with_cache = model.generate(
    input_ids,
    max_new_tokens=100,
    use_cache=True,                # B
    attention_mask=attention_mask
)
end_time_with_cache = time.time()
duration_with_cache = end_time_with_cache - start_time_with_cache
print(f"Time with KV Cache: {duration_with_cache:.4f} seconds")

# Calculate and print the speedup
speedup = duration_without_cache / duration_with_cache
print(f"\nKV Cache Speedup: {speedup:.2f}x")

在一台常规机器上的示例输出：

sql 复制代码

Time without KV Cache: 30.9818 seconds
Time with KV Cache: 6.1630 seconds

KV Cache Speedup: 5.03x

结果非常明确：仅仅打开 KV 缓存 ，生成 100 个 token 的速度就超过 5× 。对于更大的模型和更长的序列，这个加速因子往往还能再升，达到 6× 甚至更多。KV Cache 的巨大价值就在于此：通过消除重复计算，让实时、交互式生成成为可能。

不过，速度的提升也带来了代价 ------缓存不是免费的。把这些 Key/Value 矩阵存进内存，会引入一个显著的新挑战：KV Cache 的"暗面"------巨大的内存占用。

2.5 KV 缓存的阴影面：内存代价

我们已经看到 KV 缓存带来的惊人加速。通过消除冗余计算，它让交互式、长序列生成成为可能。然而，这种高效是有代价的------内存。

这不仅仅是容量问题；推理过程会受到内存带宽 的限制。每一步生成时，都必须把先前所有 token 的庞大 Key 与 Value 矩阵，从 GPU 的高带宽显存（HBM）搬运到片上计算核心。这个持续的数据搬运会成为新的性能瓶颈，这也是为什么现代面向 AI 的 GPU 设计往往更重视显存容量与带宽，甚至超过对原始算力（FLOPs）的追求。

从本质上讲，缓存是一种以空间换时间 的权衡。我们避免了重复计算 K 与 V，但必须把它们存在 GPU 显存里。对于具有长上下文窗口的大模型，这部分内存占用会成为新的主瓶颈。

2.5.1 KV 缓存公式：拆解大小

我们可以用一个直接的公式精确计算 KV 缓存所需内存。图 2.21 给出了计算各项的分解。

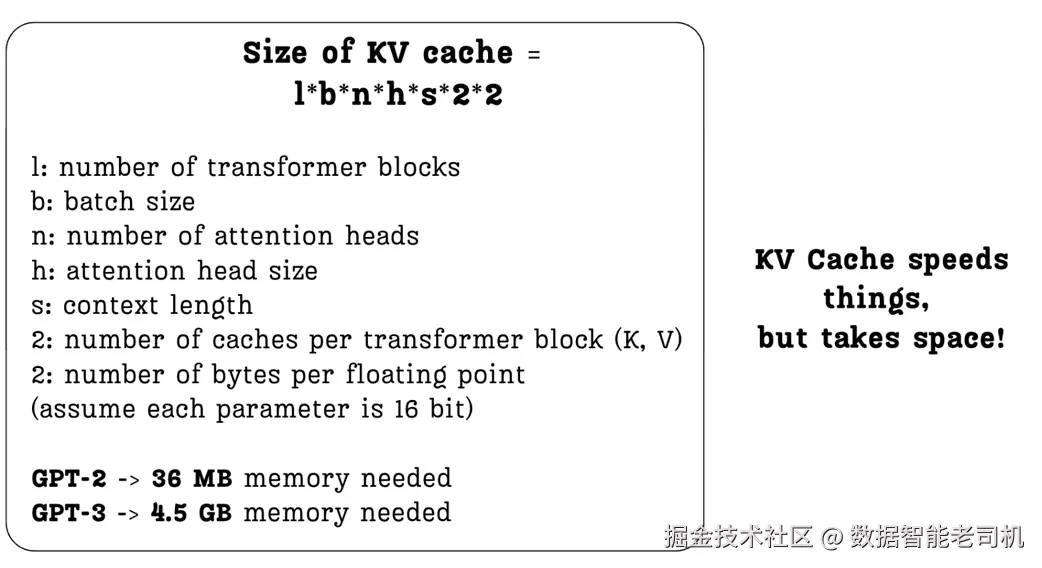
设：

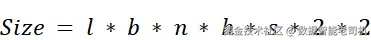
l（layers） ：Transformer 块数。每一层都需要单独的缓存。
b（batch size） ：并行处理的序列条数。
n（heads） ：每层的注意力头数。
h（head size） ：每个头的 Key/Value 向量维度。
s（sequence length） ：上下文的 token 数（关键因素）。
×2（其一） ：因为要缓存 Key 和 Value 两类矩阵。
×2（其二） ：按常见 16 位浮点（float16 或 bfloat16）计，每参数 2 字节。

公式一目了然：一旦我们想增加上下文长度 s ，或者用更大的模型（更大的 l 、n ），KV 缓存的内存就会线性增大。

图中示例显示了现实影响：

早期的 GPT-2（128M） ，KV 缓存只需约 36 MB；
GPT-3 则需要约 4.5 GB 的缓存内存，增加了 100× 以上！

2.5.2 实战中的扩展难题

这种随规模增长而"爆炸"的内存消耗，是扩展 Transformer 的基本挑战。模型越大、支持的上下文窗口越长，KV 缓存越可能成为部署的首要限制。

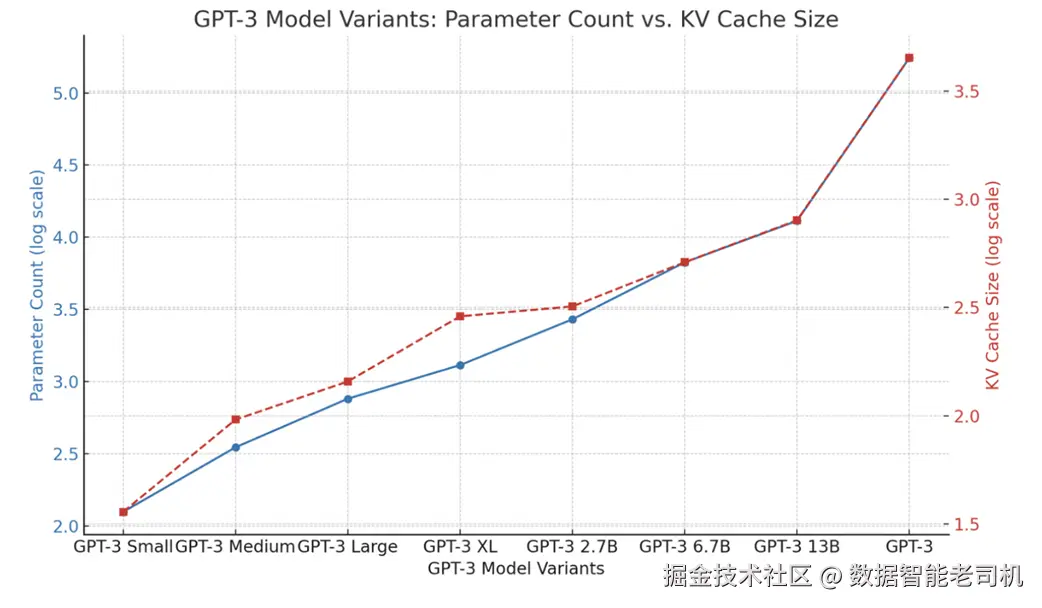
图 2.22 比较了不同 GPT-3 变体中，参数量与 KV 缓存大小的关系。可以看到二者强相关。这种内存压力限制了我们在单个 batch 中可并行处理的序列数量，也给定了在既定硬件上可支持的最大上下文长度的硬上限。

来看两个基于我们笔记的现代示例：

对于一个 30B 参数 的大模型（48 层，整体头维 n*h=7168，上下文 1024），batch size=128 时，KV 缓存约需 180 GB。这已超过大多数高端 GPU 的显存容量。
若按 DeepSeek-V3 的架构规模（61 层、128 个头、每头 128 维）并将上下文拉到 100,000 tokens ，那么单条序列 的 KV 缓存就可能约 400 GB。

这就是 KV 缓存的阴影面：它加速了计算，却吞噬了海量显存。也正因如此，很多 API 提供商（如 OpenAI）对大上下文窗口的模型定价更高------支撑这部分内存的硬件成本相当可观。

这个瓶颈促使研究者寻找更好的方法：如何在保留缓存加速的同时，显著降低内存占用？ 这把我们引向第一代结构性解决方案：多查询注意力（MQA）与分组查询注意力（GQA） 。

2.6 以内存为先的方案：多查询注意力（MQA）

若要解决 KV 缓存的内存问题，最直接 的办法是什么？**多查询注意力（MQA）**给出一个激进答案：让所有注意力头共享同一套 Key 与 Value 矩阵。

2.6.1 核心思想：共享一份 Key 与 Value

先回顾标准的多头注意力（MHA） ：在每一层里，每个注意力头都是一个"独立专家"，拥有自己独立学习的 Wk（Key 权重） 与 Wv（Value 权重） 。也就是说，在 vanilla MHA 中，每个头 都有不同的 Wk 与 Wv。

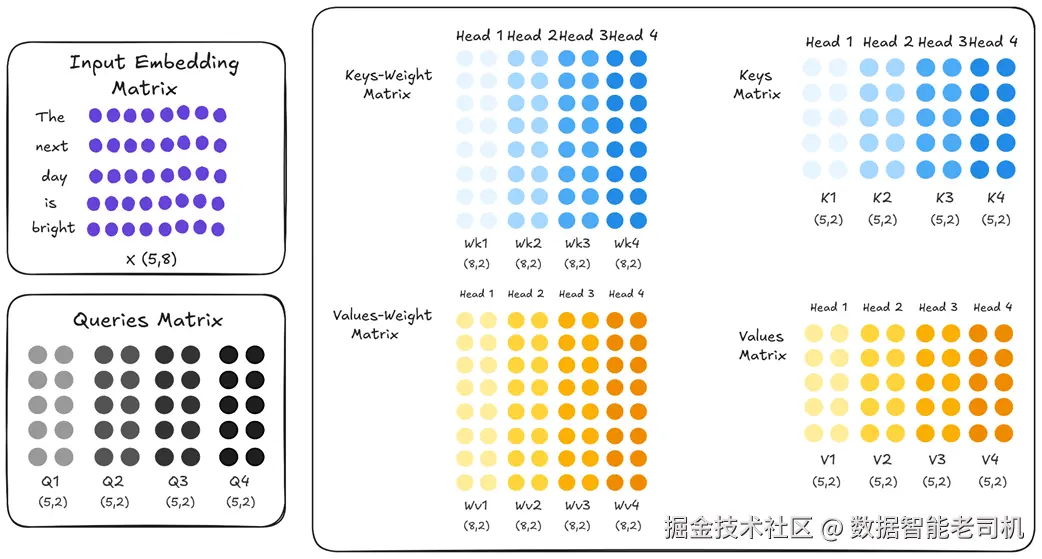
图 2.23 标准 MHA：假设有 4 个头，每个头的 Key/Value 权重矩阵（用不同颜色表示）各不相同。这种"多样性"让每个头能学到不同的模式与关注点，是 MHA 表达力的来源。

但这也是内存问题的来源：为了快速推理，我们需要为每个头 缓存完整的 Key 与 Value 矩阵。MQA 采取了直接且强硬的做法：做一个简单修改------仍然让每个头保留自己的 Query 投影 （保证每个头能提出不同"问题"），但强制所有头共享同一组 Key/Value 投影。

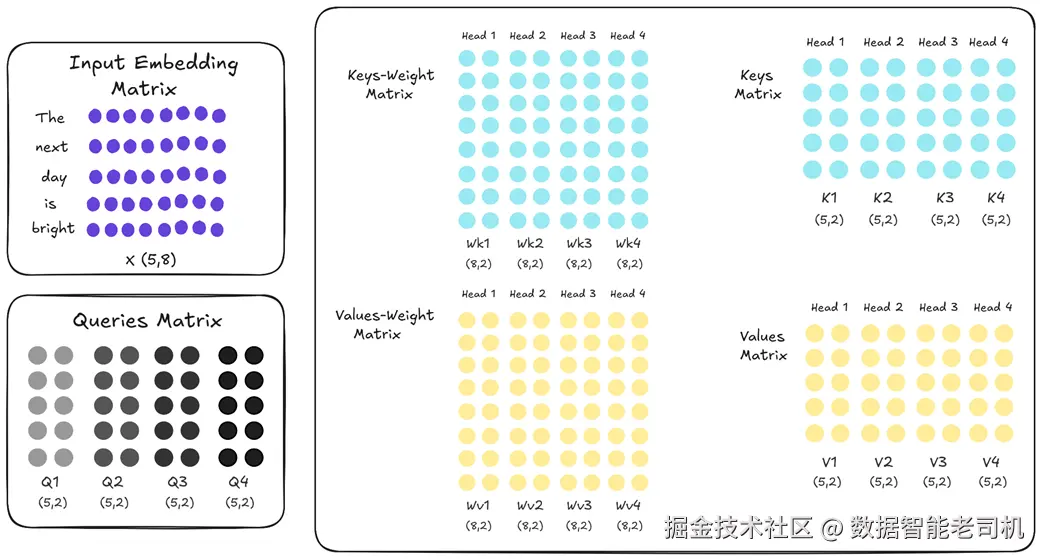
图 2.24 MQA：4 个头依然有各自独立的 Query 投影，但 Key 与 Value 的投影统一为一份共享（统一颜色）。

仔细看图 2.24 的差异：所有头的 Wk1...Wk4 现在是同一份矩阵 ，Wv 也一样。因此，当输入嵌入被投影时，得到的 K1、K2、K3、K4 实际都是完全相同的拷贝，V 亦然。

对缓存的影响立竿见影 ：我们不再需要为 4 个头分别存 4 份 Key 与 4 份 Value；只需一份 Key 与一份 Value 。推理时，4 个 Query 头将同时去跟这一共享的 K/V 交互。

这个极简的结构改动，就是 MQA 的核心。它把节省内存 放在首位。接下来我们将看到，它如何在 KV 缓存公式中带来数量级的下降，同时也将讨论它在模型表现上的不可避免的权衡。

2.6.2 对 KV 缓存公式的影响

从 MHA 切换到 MQA，会对 KV 缓存的大小产生直接而剧烈 的影响。回顾我们在 2.5.1 小节给出的公式：

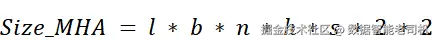
关键变量是 n （注意力头数）。在 MHA 中，因为每个头都有自己独立的 Key 与 Value 矩阵，所需内存会随头数线性增长。

在 多查询注意力（MQA） 中，由于所有头共享一份 Key 与 Value，对应地我们不再需要存储 n 份，只需1 份。公式因此变为：

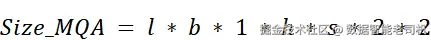
在新的公式里，原本的 n 项等效地被 1 取代（其中 n 是注意力头总数），从而消除了"随头数线性增长"的因素。KV 缓存大小因此按 n 倍缩减。

这种缩减在大模型上尤为惊人：

GPT-3（175B） ：有 96 个注意力头（n=96）。采用 MQA 后，KV 缓存可从 4.5 GB 降到约 48 MB （×96 的压缩）。
DeepSeek-V3（671B） ：有 128 个注意力头（n=128）。MQA 将其理论 KV 缓存从约 400 GB 降到 3 GB 出头 （×128 的压缩）。

这是对内存占用的惊人削减，并会直接转化为更快的推理（后文代码会看到），因为每步需要从内存加载的数据大幅减少。------那么，如果 MQA 在"内存问题"上如此有效，为什么并非所有模型都采用它呢？

2.6.3 性能权衡：表达能力的损失

MQA 带来的巨大内存节省看起来"好得令人难以置信"，但代价同样显著：模型性能与语言理解能力的下降。要理解这一权衡，我们得回到最初"为什么要用多头注意力（MHA）"。

看下面这个有歧义的句子：

"The artist painted the portrait of a woman with a brush."

至少两种解读：

解读 A（工具） ：画家用一支画笔 作画（painted with a brush）。
解读 B（属性） ：这幅女人的肖像，女人拿着一支画笔 （a woman with a brush）。

一个强大的语言模型需要同时理解并区分这两种潜在关系------这正是 MHA 设计的目的。

MHA 如何处理歧义？

在标准 MHA 中，每个头都是"独立专家"，拥有自己学习到的 Wk/Wv 。这种独立性 带来专门化：

头 1 可能专注于句法关系 （如"动词-工具"）。它的 Query 在"painted"与"brush"的 Key 之间会打出很高的注意力分数，捕捉"画画是用画笔完成的"这一语义。
头 2 可能专注于语义/描述关系 （如"名词-属性"）。它会让"woman"与"brush"之间获得较高分数，捕捉"画像中的女人与画笔相关"这一语义。

由于 K₁ ≠ K₂ 、V₁ ≠ V₂ ，各头可以并行建模不同关系，最终上下文向量融合了多种视角，这是 MHA 表达力的来源。

MQA 为什么会失去这种能力？

在 MQA 中，所有头被迫共享同一套 Key/Value：K₁ = K₂ = ...，V₁ = V₂ = ...。于是：

这唯一的 Key 矩阵无法像多个头那样分别"专精"。它必须试图通吃所有关系，只能编码一种通用表示。
当"句法专家"的 Query 和"语义专家"的 Query 都去对齐同一份 Key 时，像 "brush" 这样的词很难同时 清晰地表达"我是画画的工具"与"我是女人持有的物品"两种信号------二者势必其一被削弱甚至丢失。

这就是 MQA 的根本缺陷：

通过强制共享 K/V，MQA 大幅限制 了各头的专门化 能力，削弱模型捕捉多样且细微关系的能力，从而导致整体性能下降。

因此，MQA 是一个以内存为先 的方案。显著的性能权衡促使研究者寻找更平衡的中间地带------这将引出后文的 分组查询注意力（GQA） 。在此之前，我们先看如何把这个节省内存的 MQA 用代码实现出来。

2.6.4 从零实现一个 MQA 层

在 PyTorch 中实现 MQA 并不复杂。注意力计算的核心逻辑保持不变，唯一变化 在于 Key/Value 的投影方式 ：不再为每个头各自投影，而是只生成一份 ，随后复制给所有头使用。

下面的代码定义了一个 MultiQueryAttention 模块。请特别留意 __init__，结构差异最明显。

ini 复制代码

import torch
import torch.nn as nn
 
class MultiQueryAttention(nn.Module):
    def __init__(self, d_model, num_heads, dropout=0.0):
        super().__init__()
        assert d_model % num_heads == 0, \
            "d_model must be divisible by num_heads"
 
        self.d_model = d_model
        self.num_heads = num_heads
        self.d_head = d_model // num_heads
 
        self.W_q = nn.Linear(d_model, d_model)     #A
        self.W_k = nn.Linear(d_model, self.d_head) #B
        self.W_v = nn.Linear(d_model, self.d_head) #B
        self.W_o = nn.Linear(d_model, d_model)
 
        self.dropout = nn.Dropout(dropout)
        self.register_buffer('mask', torch.triu(
            torch.ones(1, 1, 1024, 1024), diagonal=1))
 
    def forward(self, x):
        batch_size, seq_len, _ = x.shape
 
        q = self.W_q(x).view(batch_size, seq_len, self.num_heads, 
                             self.d_head).transpose(1, 2)
 
        k = self.W_k(x).view(batch_size, seq_len, 1, 
                             self.d_head).transpose(1, 2)
        v = self.W_v(x).view(batch_size, seq_len, 1, 
                             self.d_head).transpose(1, 2)
 
        k = k.repeat(1, self.num_heads, 1, 1)  #C
        v = v.repeat(1, self.num_heads, 1, 1)  #C
 
        attn_scores = (q @ k.transpose(-2, -1)) / (self.d_head ** 0.5)
 
        attn_scores = attn_scores.masked_fill(
            self.mask[:,:,:seq_len,:seq_len] == 0, float('-inf'))
 
        attn_weights = torch.softmax(attn_scores, dim=-1)
        attn_weights = self.dropout(attn_weights)
 
        context_vector = (attn_weights @ v).transpose(1, 2) \
            .contiguous().view(batch_size, seq_len, self.d_model)
 
        output = self.W_o(context_vector)
        return output

关键差异解析：

Key/Value 投影 ：在标准 MHA 中，W_k/W_v 的输出维度通常是 d_model，随后再拆成 num_heads × d_head。而在 MQA 中，它们直接投影到 d_head （单头大小），因为我们只生成一份 K/V，而不是按头数生成再切分。
重复 K/V ：在 forward 中，先计算这一份 K/V，然后通过 .repeat() 按头数"展开" 给所有 Query 头使用。实践里这通常只是"视图式"的扩展（或广播友好处理），不会像复制大矩阵那样成倍占用内存，从而高效实现"共享"。
效率收益 ：最大收益来自缓存张量的缩减 。标准 MHA 要缓存形如 (batch_size, num_heads, seq_len, d_head) 的 K/V；而 MQA 只需缓存 (batch_size, 1, seq_len, d_head)，内存占用显著降低。

通过这个实现，我们得到一个以内存优化为目标 的注意力层；它在显存与带宽上极度友好，但也带来了前述的表达力权衡 。这为我们探索更折中、均衡的方案（如 GQA）做好了铺垫。

2.7 中间道路：分组查询注意力（GQA）

将模型表达力换取内存效率并不理想。这促使研究者寻找一种更均衡的方案------既能显著节省内存、又不完全牺牲多头设计带来的能力。这个方案就是分组查询注意力（GQA） 。

GQA 在 MHA 的高表达力 与 MQA 的高内存效率 之间给出务实折中；它提供一个可调的"旋钮"，以平衡这两者的取舍。

2.7.1 核心思想：在组内共享 Key 与 Value

GQA 的核心思想既简单又有效：不是让所有注意力头共享同一套 Key/Value（像 MQA 那样），而是把注意力头分组，仅在组内共享 Key 与 Value。

以 4 个头为例，我们不再把 4 个头当作一个整体（MQA 的做法），而是把它们分成两个组。

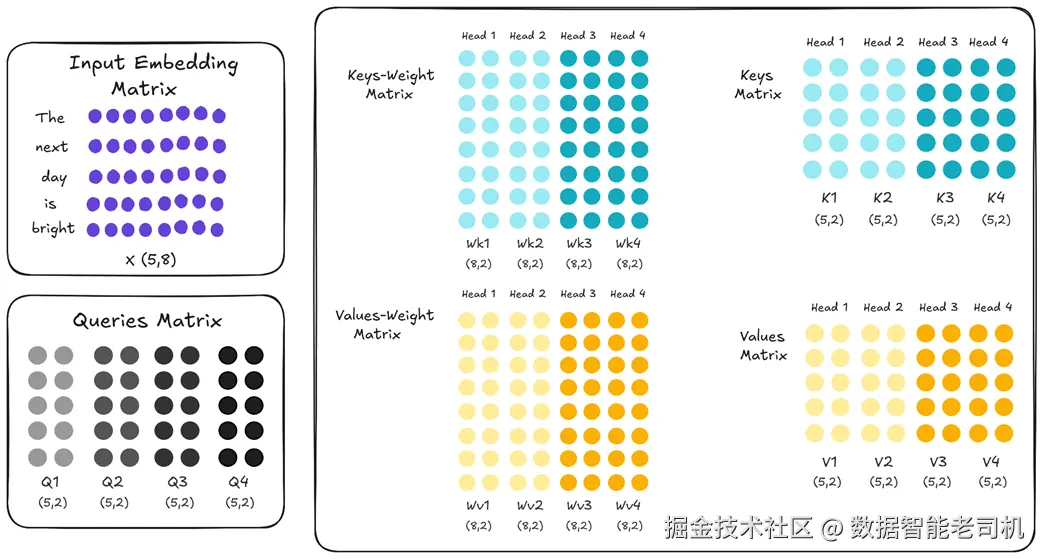
图 2.25 分组查询注意力（GQA）。 四个注意力头被分成两组。组 1（浅蓝/浅黄）中的头 1 和头 2 共享同一套 Key/Value 投影；组 2（深蓝/深黄）中的头 3 和头 4 共享另一套不同的 Key/Value 投影。

如图示：

组 1 内：头 1 与头 2 共享相同的 Wk/Wv，得到的 K1 与 K2 完全相同，V1 与 V2 也相同。
组 2 内：头 3 与头 4 共享另一套 Wk/Wv，K3=K4、V3=V4。
组间：组 1 的 Key/Value 与组 2 的 Key/Value 彼此不同（浅蓝与深蓝）。

这种分组策略优雅地化解了 MQA 的主要缺点：我们不再强迫所有头看同一信息。现在，组 1 的头与组 2 的头拥有不同的 Key/Value，可各自专门化、捕捉不同视角，类似标准 MHA 的多样性。

同时，相比 MHA，内存仍有显著节省：不再缓存 4 份独立的 Key 矩阵，而只缓存 2 份（每组 1 份）。GQA 在性能与内存之间提供一个"中间地带"的解法。

2.7.2 可调旋钮：在内存与性能间取舍

GQA 中的"分组"引入了一个强大的可调旋钮 ：组数 g。它直接决定内存与表达力的平衡点。

回顾 KV 缓存大小公式：

MHA ：随头数 n 线性增长；
MQA ：相当于把 n 换成 1；
GQA ：随组数 g 线性增长。公式变为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> Size GQA = l × b × g × h × s × 2 × 2 \text{Size}_{\text{GQA}} = l \times b \times g \times h \times s \times 2 \times 2 </math>SizeGQA=l×b×g×h×s×2×2

据此得到一条连续光谱：

若设 g = n ，GQA ≡ MHA ------ 性能最大 、内存最大；
若设 g = 1 ，GQA ≡ MQA ------ 内存最省 、性能最低；
选取 1 < g < n，即可在中间找到实用的折中点。

例如 Llama 3 8B 共有 32 个注意力头。它采用 g=8 的 GQA：每 4 个查询头共享一套 Key/Value。这样 KV 缓存从 32 份降到 8 份，缩小 4 倍；相较 MQA，它保留了更多表达力，因此成为众多开源 LLM 的热门选择。

不过这本质上仍是折中：我们用一定的表达力损失换取内存下降。GQA 巧妙而有效，但并未改变"性能↔内存"的根本张力------它只是让我们能在这条曲线上选到一个更舒服的位置。

这也促使 DeepSeek 团队提出一个更深刻的问题：能否根本性改变这种取舍？是否可以在保留"每个头独立投影（MHA 的全部表达力）"的同时，仍然显著降低内存？

答案是可以 ------方案就是多头潜表示注意力（MLA） 。在进入这项突破性技术前，我们先通过手写实现来加深对 GQA 的理解。

2.7.3 从零实现一个 GQA 层

实现 GQA 是在 MQA 代码基础上的自然扩展：区别在于不再只有1 份共享的 Key/Value 投影，而是有 num_groups 份；同时确保每组的查询头只对齐其对应的 Key/Value 组。

下面给出 GroupedQueryAttention 模块。关键变量是 num_groups，它就是前述的"可调旋钮"，直接决定 Key/Value 投影的份数，从而在内存节省 与模型性能间寻求平衡。

ini 复制代码

import torch
import torch.nn as nn
 
class GroupedQueryAttention(nn.Module):
    def __init__(self, d_model, num_heads, num_groups, 
                 dropout=0.0, max_seq_len: int = 0):
        super().__init__()
        assert d_model % num_heads == 0, \
            "d_model must be divisible by num_heads"
        assert num_heads % num_groups == 0, \
            "num_heads must be divisible by num_groups"
 
        self.d_model = d_model
        self.num_heads = num_heads
        self.num_groups = num_groups
        self.d_head = d_model // num_heads
 
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, 
                             self.num_groups * self.d_head)  # A
        self.W_v = nn.Linear(d_model, 
                             self.num_groups * self.d_head)  # A
        self.W_o = nn.Linear(d_model, d_model)
 
        self.dropout = nn.Dropout(dropout)
        # 可选的因果掩码预分配
        self._register_mask_buffer(max_seq_len)
 
    def forward(self, x):
        B, T, _ = x.shape
        
        q = self.W_q(x).view(B, T, self.num_heads, 
                             self.d_head).transpose(1, 2)
        k = self.W_k(x).view(B, T, self.num_groups, 
                             self.d_head).transpose(1, 2)  # B
        v = self.W_v(x).view(B, T, self.num_groups, 
                             self.d_head).transpose(1, 2)  # B
 
        heads_per_group = self.num_heads // self.num_groups
        k = k.repeat_interleave(heads_per_group, dim=1)  # C
        v = v.repeat_interleave(heads_per_group, dim=1)  # C
 
        # 标准注意力计算
        attn_scores = (q @ k.transpose(-2, -1)) * (self.d_head ** -0.5)
        causal_mask = self._get_causal_mask(T, x.device)
        attn_scores = attn_scores.masked_fill(causal_mask, float("-inf"))
        attn_weights = torch.softmax(attn_scores, dim=-1)
        attn_weights = self.dropout(attn_weights)
        
        context = (attn_weights @ v).transpose(1, 2).contiguous() \
                  .view(B, T, self.d_model)
        
        return self.W_o(context)
 
    # 掩码管理辅助方法
    def _register_mask_buffer(self, max_seq_len):
        if max_seq_len > 0:
            mask = torch.triu(torch.ones(1, 1, max_seq_len, max_seq_len,
                                         dtype=torch.bool), diagonal=1)
            self.register_buffer("causal_mask", mask, persistent=False)
        else:
            self.causal_mask = None
 
    def _get_causal_mask(self, seq_len, device):
        if self.causal_mask is not None and \
           self.causal_mask.size(-1) >= seq_len:
            return self.causal_mask[:, :, :seq_len, :seq_len]
        return torch.triu(torch.ones(1, 1, seq_len, seq_len, 
                                     dtype=torch.bool, device=device),
                          diagonal=1)

这个实现体现了"可调旋钮"的思想：只需改变 num_groups，就能在 MQA-like（num_groups=1） 与 MHA-like（num_groups=num_heads） 的行为之间平滑切换。

2.8 性能 vs 内存：取舍的本质

至此我们回顾了第一代针对 KV 缓存内存危机的方案：MQA 与 GQA。二者都能显著缩小 KV 缓存的内存占用，使在现有硬件上运行更大的模型与更长的上下文成为可能。

但它们的共同之处在于：都是通过减少独立的 Key/Value 投影数 来省内存------这必然引出表达力的牺牲：

MQA 是最极端的做法：把 n 个 K/V 头压成 1 个；
GQA 给出折中：把 n 个头压成 g 个组。

GQA 让我们能在"性能---内存"曲线上选一个更合适的点，但没有改变曲线本身 ：我们依旧要在 MHA（性能最好） 与 MQA（内存最省） 之间，或**GQA（介于两者）**中做选择。

这份未解的张力，正是 DeepSeek 架构之所以创新的原因。DeepSeek 问了一个不同的问题：与其减少头的数量，能否让每个头内部的信息更紧凑？能否直接压缩 Key/Value 本身？

这种思路的转变------从"减少头"到"压缩信息"------直接引向下一章的 多头潜表示注意力（MLA） ：一种力图同时保持 MHA 的充分表达力 与 显著内存节省 的根本性方案。

2.9 小结

自回归生成在朴素实现中会在每步重算整段上下文，导致 O(n²) 的计算复杂度；
KV 缓存 通过存储历史 Key/Value，将推理转为 O(n) ，显著加速；
但 KV 缓存引入严峻的内存瓶颈，其大小随序列长度、层数与头数线性增长；
MQA 通过让所有头共享一套 K/V，将缓存显著压缩，但因失去头的专门化而影响性能；
GQA 通过"分组共享"，在内存与表达力间提供可调折中；
这类方案的本质是减少独立 K/V 的数量，因此固有地存在"内存效率 ↔ 表达力"的取舍。

下一章我们将看到 DeepSeek 的关键突破 MLA ：它尝试在保留多头表达力 的同时，以压缩 K/V 信息 的方式实现大幅内存节省。