对于数据结构:堆的超详细保姆级解析——下（堆排序以及TOP-K问题）

开篇介绍:

hello 大家，我们又见面了，在上一篇博客中，我们共同探索了如何实现堆这么一个数据结构，相信大家经过上篇博客的学习，对堆的了解程度以及掌握程度，都有了极大的水平提升。

那么堆，有什么用呢？首先，作为一个数据结构，它肯定具有存储数据的功能，这是毋庸置疑的，但是呢，我们知道，堆有大堆和小堆之分，那么那么，这一个知识点，蕴含着什么秘密呢？

诶，不错，就是我们标题所说的------堆排序，我们之前学过了冒泡排序以及qsort函数排序，但是呢说实话，这两种排序方式，效率都不高，说难听一点就是在现实中，dog都不用，因为它们的时间复杂度，实在是太高太高了，所以，这也就意味着，我们要去掌握一些更有效率，更高效，更快速，时间复杂度以及空间复杂度更低的排序算法。

而堆排序，就是其中一种，所以，在本篇博客中，我就将带领着大家将堆排序给解析的彻彻底底，同时，我也会对TOPK问题，进行详细的解析。

话不多说，我们直接进入正题，温馨提示:下面的内容对数学的要求可能会稍稍高了一些，但是也并不会多难，大家大可放心，相信自己。

我们，出发喽～

堆排序:

那么堆排序，它的原理是什么呢？我们知道，一般来说，我们对数据进行排序，其实就是把原本无序的数据排成有序的数据，这个数据可以是升序的，也可以是逆序的，升序就是从前到后是从小到大，而逆序则是从前到后是从大到小。

那么大家开动小脑筋仔细想想，这个升序和降序，oi，和我们的小堆和大堆，有什么关系呢？快想想，不相信你想不出来。

啊哈，答案很简单，我们知道，小堆是父节点的数据要小于子节点的数据大小，那么，我们的小堆的根节点，是不是就是整个堆里面，数据最小的那一个，这个大家应该能理解，不能理解的话，再去复习复习上一篇博客哦大家。而大堆呢，是父节点的数据要大于子节点的数据，那么那么，我们的大堆的根节点的数据大小，是不是就是整个大堆里面，数据最大的一个点呢？大家不妨画图理解。

这里我想先给大家强调一个点，那就是，在我们的堆排序中，如果你想升序排列数据，那你就得用大堆，而如果你想降序排列数据，那么你就得用小堆，原因是什么呢？其实很简单，这主要是与我们下面的取出堆顶元素（也就是上篇博客所讲的hptop函数）有关，大家看到下面就能理解了

那么，先假设我们有一个堆，就假设它是大堆吧，上节课主要讲小堆，这节课我们尽量以大堆为主，加强大家理解，我们假设有下图这么一个大堆，OK，大家不难看出，这个大堆中，数据最大的点，就是根节点。

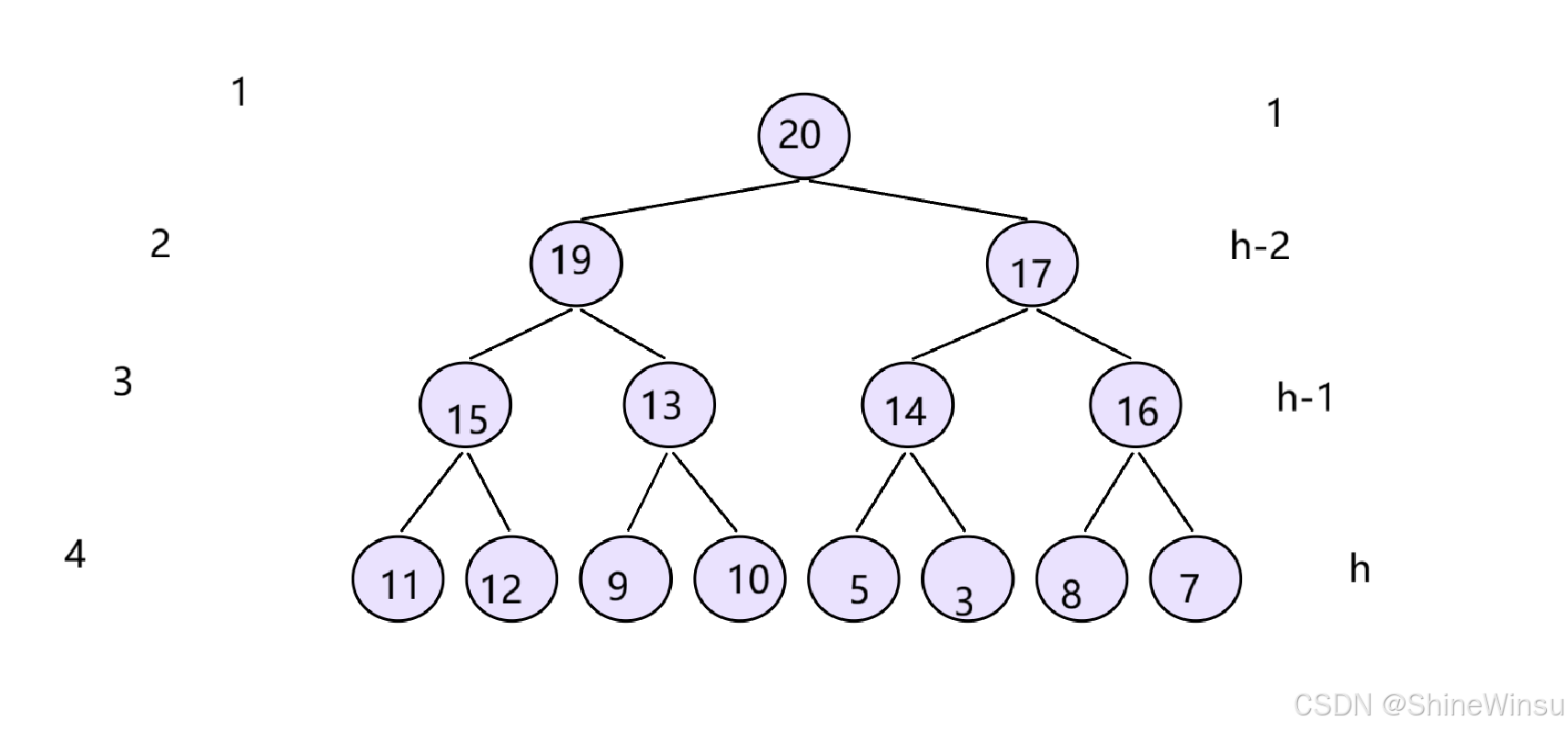
那么，我们如何根据这个大堆，去将一个无序的数组（要牢记，堆的本质就是数组，不要理所当然的认为，当一个数组成了堆之后，它就有序了，这是不对的，就比如上图所示），其实，想要实现的关键，就是，根节点。

我们接下来以用大堆实现升序排列为例子，带大家好好剖析一番，同时，也将引入我们堆排序的第一个方法

堆排序方法一:

这个方法一呢，其实效率不高，主要是给大家熟悉一下堆排序的一个思路用的，那么在正式讲述方法一之前，我这边还是建议大家，把上一篇博客的hptop函数，hppop函数，向下调整算法，向上调整算法，再好好好好地熟练一下。

OK，我们发车。

那么其实这个思路也是很简单的，假设我们有一个堆，就比如下图这个堆，

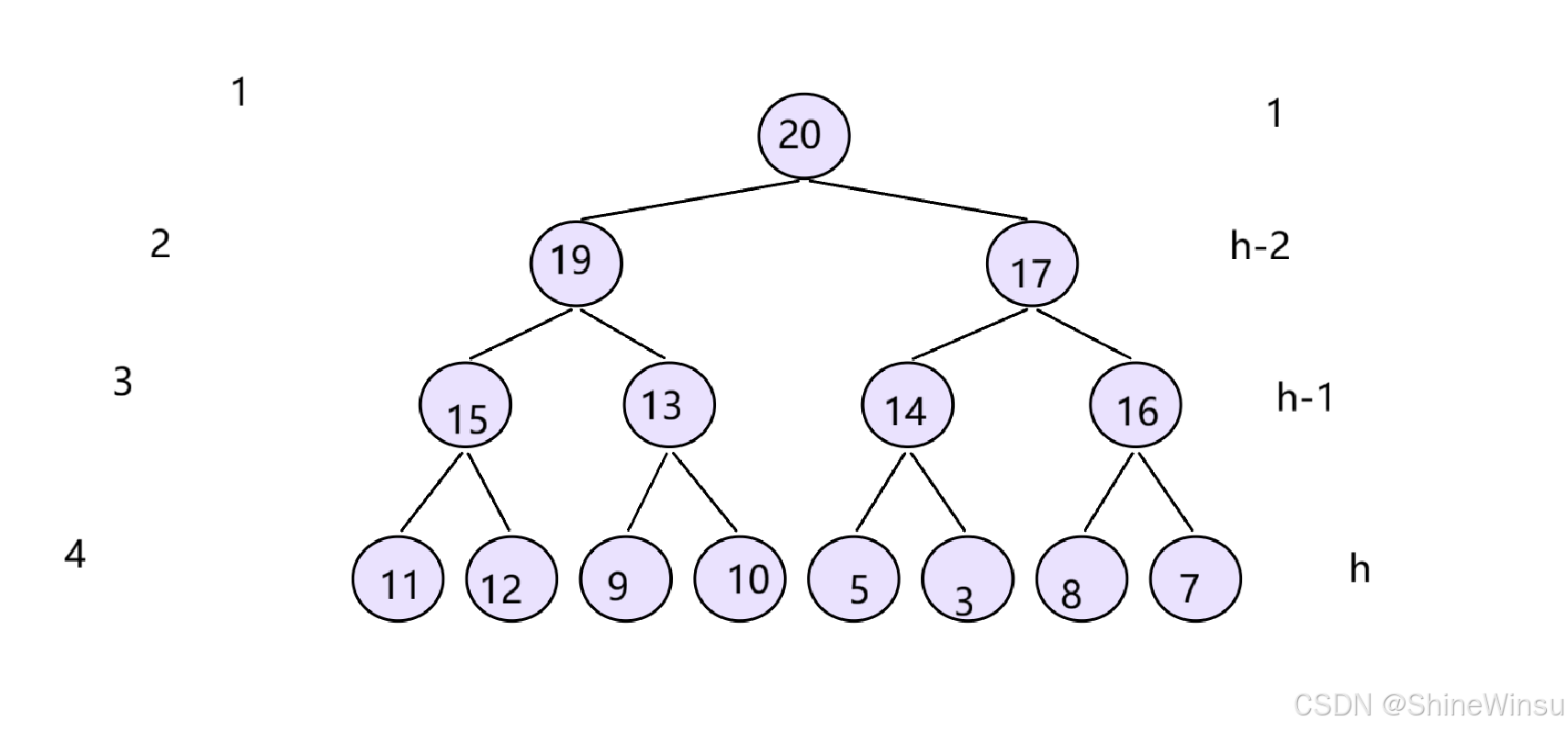
那么我们如何利用hptop函数和hppop函数，去将堆排序实现呢？

首先，我们复习一下hptop函数，这个函数是不是每次都能把一个堆的根节点给保存下来，然后再把这个根节点的值返回，而后我们进行hppop函数，也就是对堆顶（根节点）数据的删除，而且在删除函数中呢，当我们对根节点删除了数据之后，我们利用向下调整算法，将删除数据后不成规律的堆，给它继续形成一个符合规律的大堆。

诶，关键点来了大家，那么这个继续形成一个符合规律的大堆，是不是就代表着此时这个大堆的根节点的数据，就又是新大堆的数据最大的节点呢？而且大家如果仔细观察一下，很容易就能发现，这个新的大堆的根节点的数据大小，其实就是旧大堆的的倒二个大的数据呢？

大家看看下图，就能理解。

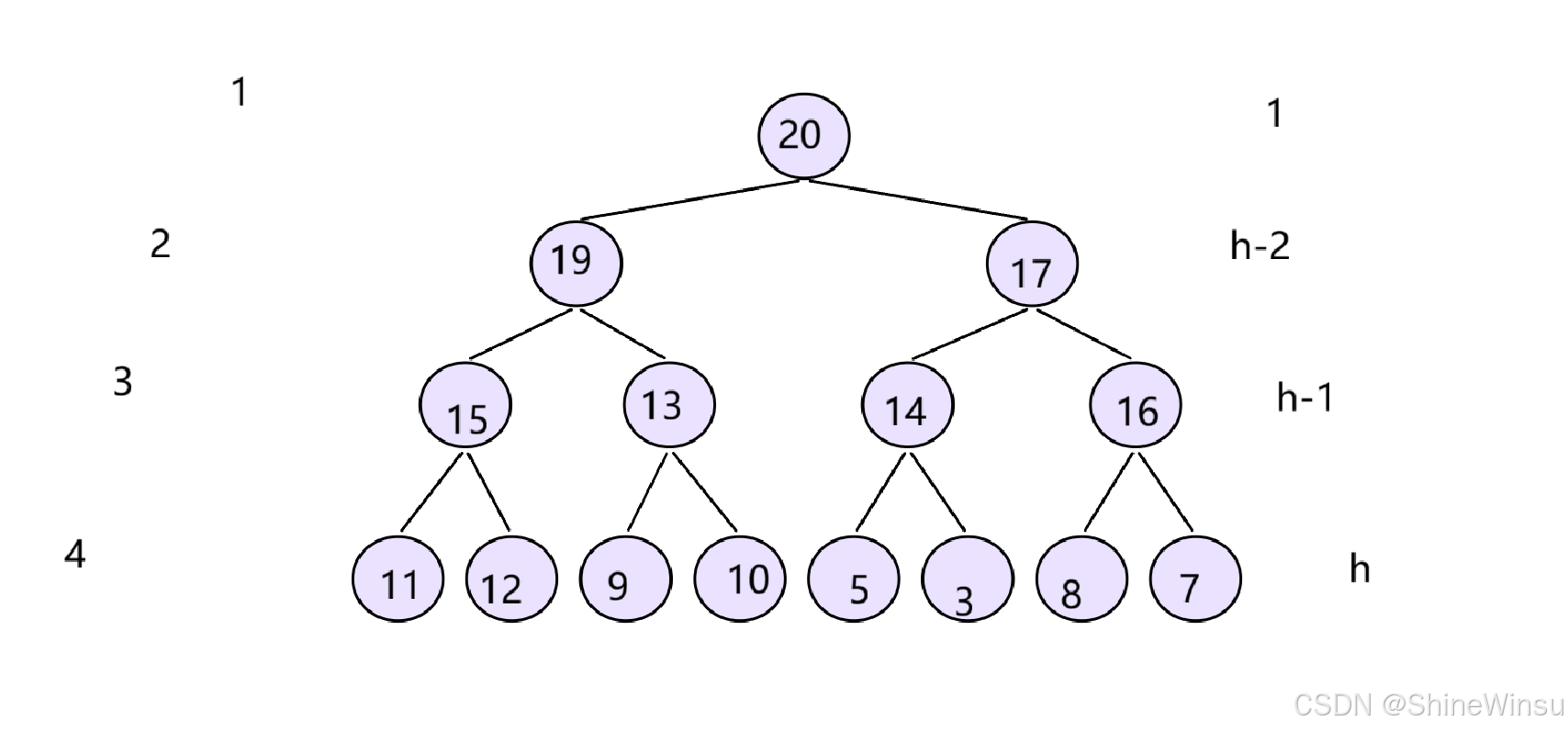
此时，我们新的大堆，就是如下这个（已经把原大堆的根节点（也就是最大数据）给删除了），那么那么，这个时候，诶，我们重复上面的步骤，吼吼，大家脑海中想想加模拟运行一下，是不是，是不是，是不是就完美实现了，每次我们取出的堆顶元素都是一个新堆的最大的数据，希望大家一定要把自己的脑子锻炼成一个小计算机，毕竟，计算机没有眼泪，工科之王～

为了方便大家理解，我给大家提供一个图，详细模拟了上面所说的步骤，大家看了之后就能明白。

在这里，我必须再强调一点，那就是取出堆顶元素之后，必须要进堆的数据删除，不难，是无法正常进行堆排序的，大家看一下下图，应该就能理解，o～～～k～～～～。

那么我们的根本目的，是将原本无序的数组给排好，而在上面的步骤中，我们仅仅只是取出了堆顶元素，还没有排好序呢，那么，在我们的这个方法一中，其实就是再创建一个数组，去接收每次取出的堆顶元素，当堆被删除的一个数据不剩之后，此时的数组，不就是一个升序的数据排列了吗。

完整代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

// 堆的数据结构定义（大根堆）
typedef int HPDataType;
typedef struct Heap
{
    HPDataType* a;  // 存储堆元素的数组
    int size;       // 当前堆中元素的数量
    int capacity;   // 堆的容量
} HP;

// 初始化堆
void HPInit(HP* hp)
{
    assert(hp);
    hp->a = NULL;
    hp->size = 0;
    hp->capacity = 0;
}

// 销毁堆
void HPDestroy(HP* hp)
{
    assert(hp);
    free(hp->a);
    hp->a = NULL;
    hp->size = hp->capacity = 0;
}

// 交换两个元素
void Swap(HPDataType* p1, HPDataType* p2)
{
    HPDataType tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

// 向上调整（用于插入元素）
void AdjustUp(HPDataType* a, int child)
{
    int parent = (child - 1) / 2;
    while (child > 0)
    {
        // 大根堆：如果子节点大于父节点，则交换
        if (a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            child = parent;
            parent = (child - 1) / 2;
        }
        else
        {
            break;  // 满足堆的性质，停止调整
        }
    }
}

// 向下调整（用于删除元素）
void AdjustDown(HPDataType* a, int size, int parent)
{
    int child = parent * 2 + 1;  // 先假设左孩子是较大的那个
    while (child < size)
    {
        // 比较左右孩子，找到较大的那个
        if (child + 1 < size && a[child + 1] > a[child])
        {
            child++;
        }
        
        // 如果子节点大于父节点，则交换
        if (a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;  // 满足堆的性质，停止调整
        }
    }
}

// 向堆中插入元素
void HPPush(HP* hp, HPDataType x)
{
    assert(hp);
    
    // 检查容量，如果不足则扩容
    if (hp->size == hp->capacity)
    {
        int newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
        HPDataType* tmp = (HPDataType*)realloc(hp->a, newCapacity * sizeof(HPDataType));
        if (tmp == NULL)
        {
            printf("realloc failed\n");
            exit(-1);
        }
        hp->a = tmp;
        hp->capacity = newCapacity;
    }
    
    // 插入元素并调整堆
    hp->a[hp->size] = x;
    hp->size++;
    AdjustUp(hp->a, hp->size - 1);
}

// 从堆中删除顶部元素
void HPPop(HP* hp)
{
    assert(hp);
    assert(hp->size > 0);  // 确保堆不为空
    
    // 交换顶部元素和最后一个元素
    Swap(&hp->a[0], &hp->a[hp->size - 1]);
    hp->size--;
    
    // 向下调整，维持堆的性质
    AdjustDown(hp->a, hp->size, 0);
}

// 获取堆顶元素
HPDataType HPTop(HP* hp)
{
    assert(hp);
    assert(hp->size > 0);  // 确保堆不为空
    return hp->a[0];
}

// 检查堆是否为空
int HPEmpty(HP* hp)
{
    assert(hp);
    return hp->size == 0;
}

// 堆排序（升序）
void HeapSort(int* a, int n)
{
    if (n <= 1) return;  // 边界条件处理
    
    HP hp;
    HPInit(&hp);
    
    // 将所有元素插入堆中，构建大根堆
    for (int i = 0; i < n; i++)
    {
        HPPush(&hp, a[i]);
    }
    
    // 从堆中依次取出最大元素，放入数组
    int i = 0;
    while (!HPEmpty(&hp))
    {
        a[i++] = HPTop(&hp);  // 取出堆顶最大元素
        HPPop(&hp);           // 删除堆顶元素，重新调整堆
    }
    
    // 释放堆占用的内存
    HPDestroy(&hp);
}

// 测试函数
int main()
{
    int a[] = {3, 1, 2, 5, 4, 6, 8, 7, 9};
    int n = sizeof(a) / sizeof(a[0]);
    
    printf("排序前: ");
    for (int i = 0; i < n; i++)
    {
        printf("%d ", a[i]);
    }
    printf("\n");
    
    HeapSort(a, n);
    
    printf("排序后: ");
    for (int i = 0; i < n; i++)
    {
        printf("%d ", a[i]);
    }
    printf("\n");
    
    return 0;
}

如上，就是就是我们堆排序的第一个方法，但是正如我前面所说，这第一个方法其实不怎么样，为什么呢？因为大家其实不难看出，方法一我们还需要创建一个数组去接收数据，那么这也就代表，我们方法一的空间复杂度是O（N），OiOi，看着不高，但是在我们现如今这个效率为王，简略为霸的时代，如果能有更好的方法，那么自然也就不可能要这个方法一。

那么，有没有更好的方法呢？肯定有的，这是毋庸置疑的，大家，而这个方法也就是我接下来要讲的方法二。

但是在我讲方法二之前，我想先给大家讲一讲，我们上一篇博客所学的向上调整算法的时间复杂度以及向下调整算法的时间复杂度，这个，是我们理解并使用方法二的关键前提。

依然，大家可以先去复习一下我之前所写的关于时间复杂度的详细解析的博客。

接下来，我们就可以发车了。

向下调整算法的时间复杂度：

大家先看图：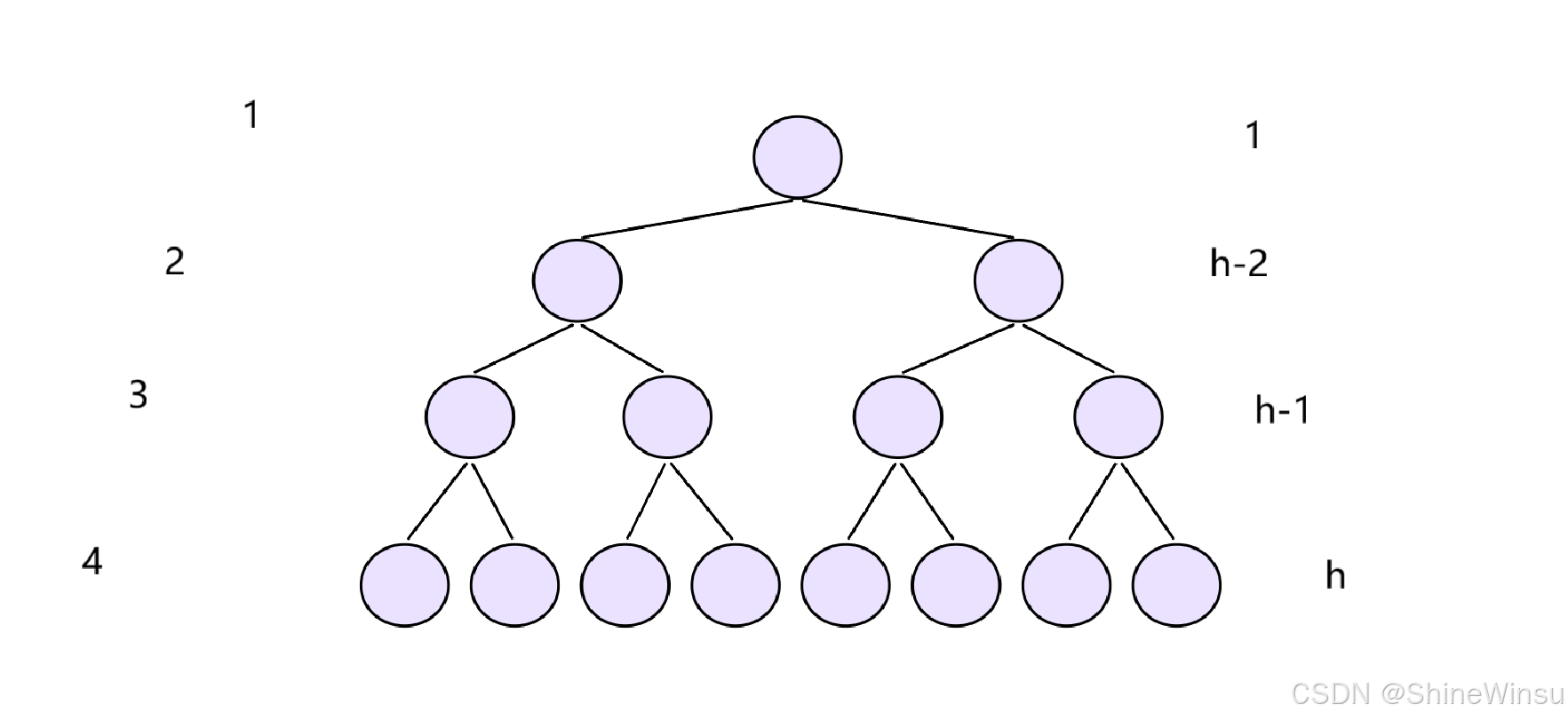

首先，我们可以解决一下，对于高为h层的满二叉树，它一共的节点有多少个？

这边解释一下为什么要用满二叉树，而且为什么下面是极端情况，这是和时间复杂度的要求有关，想要得出时间复杂度，是要求考虑最极端的情况的，那么对于完全二叉树来说，它的极端情况不就是满二叉树吗？所以，希望大家理解。

那么因为是二叉树，它的定义大家应该也明白，就是每个父节点都要有两个子节点，那么也就是说，第一层有1个节点，而第二层就有2个节点，第三层就有4个节点，以此类推，第四层就是2^（4-1）=2^3个节点，也就是8个节点，那么对于第h层，就是有2^(h-1)个节点，这个大家应该可以理解。

所以，对于满二叉树而言，对于h层而言，它就有2^0+2^1+2^3+......2^(h-2)+2^(h-1)个节点，再根据等比数列求和公式，我们不难得出，一共就是有2^（h）-1个节点，这个大家应该能够理解吧。

接下来，我们再来看看，对于某一层，如果它要进行向下调整算法的话，最坏也就是最极端的情况下，它需要进行几次向下？快想想大家。

我们依旧是拿上图作为例子，对于第一层，也就是我们的根节点，大家不难发现，根据向下调整算法的遍历而言，它最极端的情况下应该是要进行

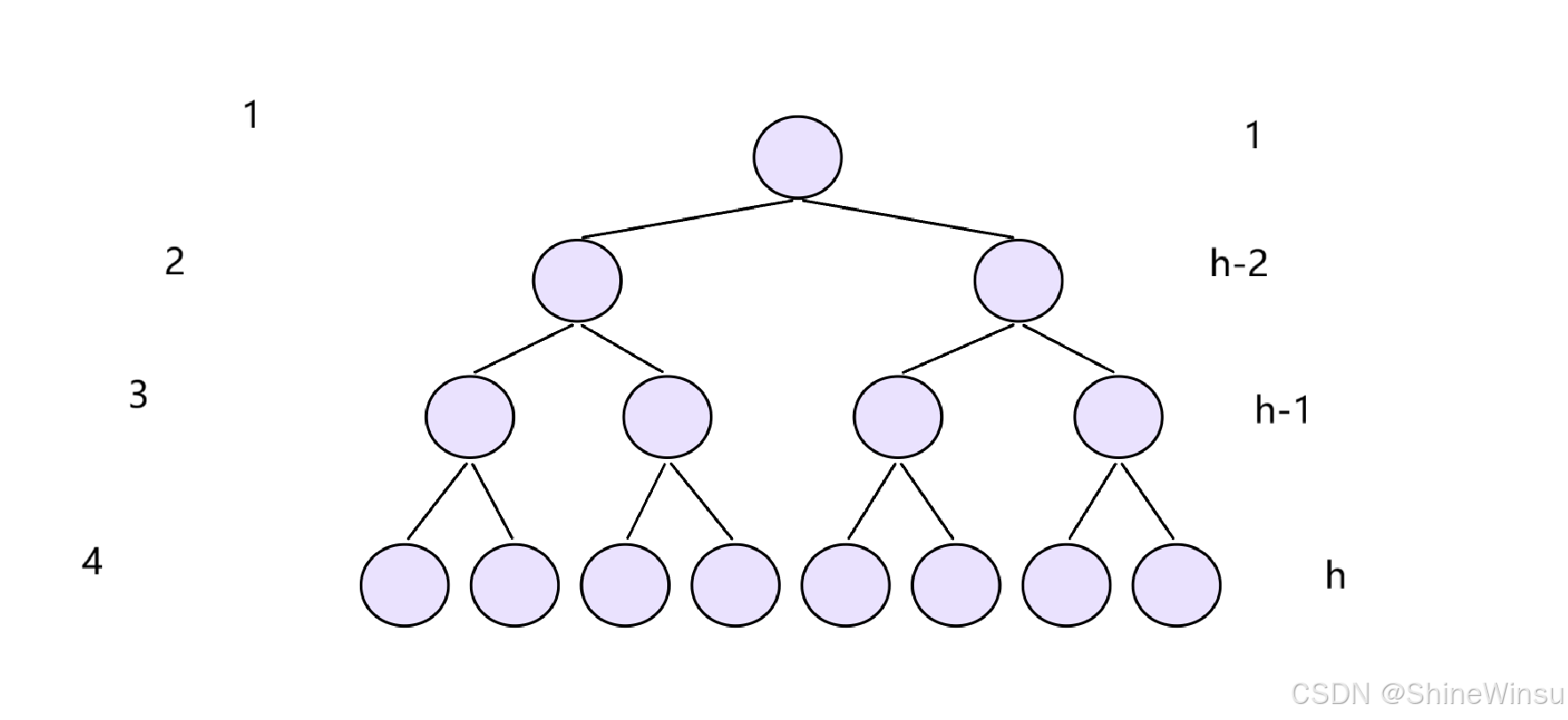
它最极端的情况下应该是要进行3次遍历（也就是要向下遍历3层），也就是先比较第二层的节点，然后再比较第三层的节点，最后再比较第四层的节点，所以，也就是要进行3次遍历。

那么我想办法用h去表示要进行几次遍历（其实就是要向下遍历几层），根据上图，大家不难看出，对于第一层，需要向下遍历h-1层，而对于第2层，则需要向下遍历h-2层，对于第3层，则是需要向下遍历h-2层，其实这个应该也是很好算的大家，因为我们最后一层的层数就是h，那么从第n层到第h层要走多少层，不就是要走h-n层吗。

那么对于第h-2层，就是要走2层，对于第h-1层，就是要走1层，是这个道理吧大家，没问题吧大家。

那么这个时候，我们就可以开始着手于计算，向下调整算法的时间复杂度了，通过上面的讲述，大家应该知道，对于一些数据，想要让它从上到下，进行调整为大/小堆，在最极端的情况下，

需要移动结点总的移动步数为：每层结点个数 * 向下调整次数

这个的原因很简单，因为对于每一层的每一个节点，我们都是有可能进行向下遍历的，那么我们又考虑的是最极端的情况下，那么自然就是需要移动结点总的移动步数为：每层结点个数 * 向下调整次数，大家应该不难理解。

那么我们可以得到，对于h层的满二叉树，它的移动节点的总的移动步数就是：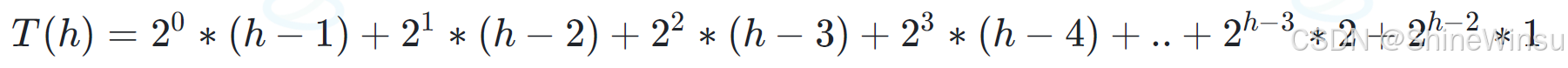

大家对这个公式有不明白的，可以结合上图进行分析。

那么这个时候，对于这么长一串的表达式，我们要怎么将它化简呢？

啊啊啊啊啊啊啊，是什么是什么？是数学！！！

是的各位，这就是为什么我上面说，需要大家的数学了，其实大家仔细观察一下，很容易就能发现，这不就是等差数列*等比数列吗？

我滴娘我滴奶，等差数列*等比数列！等差数列*等比数列！

是！！！错位相减！！！！！！

是的，我们就是用错位相减来对这个式子进行化简。

那么要怎么错位相减呢？额，这个劳烦大家其他平台搜索一下，会有很多讲解的，这里我就不班门弄斧了。

我们直接看过程：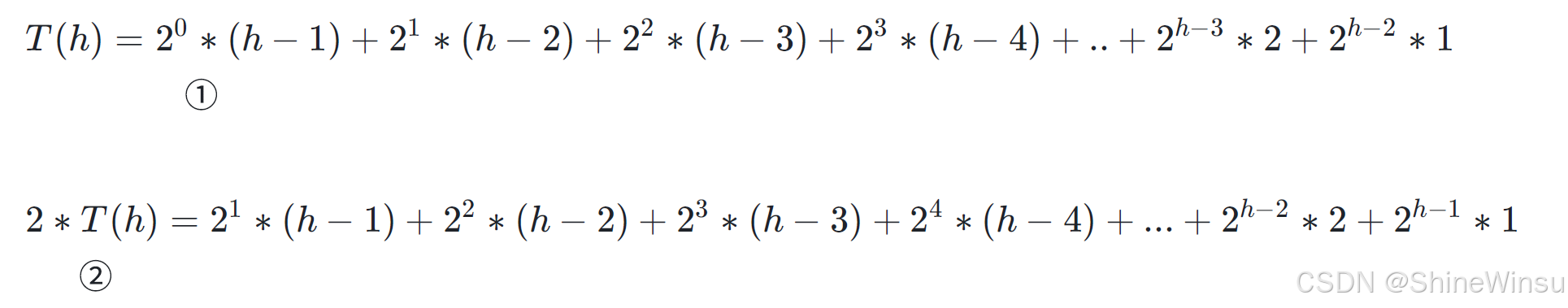

那么这个时候，我们再错位相减：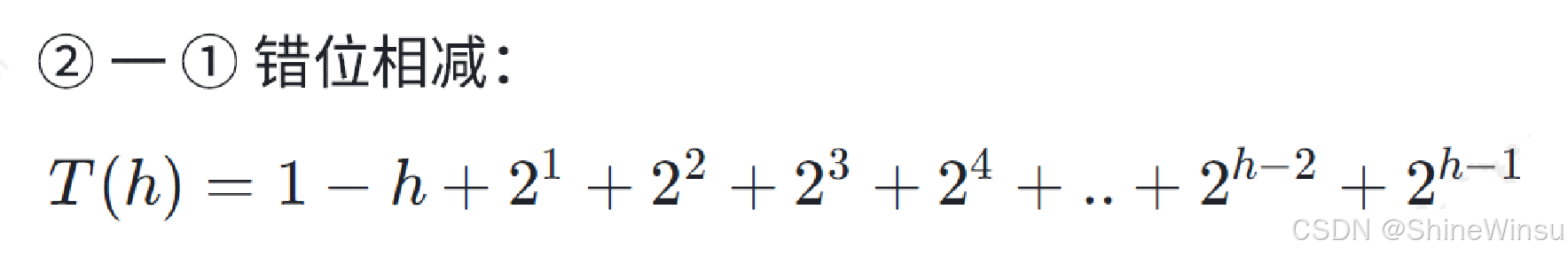

到这里还不够，我们还要进行化简：

把上面的1变为2^（0），h丢到最后面，诶，我们是不是又形成了一个关于2的等比数列

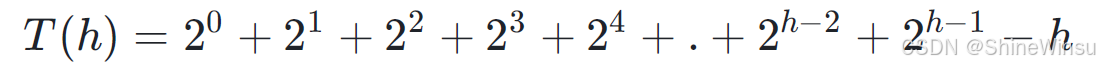
那么这个时候，我们把等比数列求和一下：

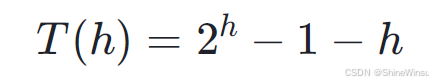
ok，得到最终结果，那么这个又怎么和时间复杂度联系起来呢？大家可不要想当然的以为，移动的总步数就是时间复杂度了，这个差远了。

因为上面得到的公式只和二叉树的层数h有关，和我们的数据总规模是无关的，换句话来说就是，我们要想办法把上面这个式子去和二叉树的数据总个数联系起来，这样子最后得到的公式，才是最终的也是正确的时间复杂度。

这主要还是因为，我们的时间复杂度中的N（T（N））是需要运行的总次数，而不是什么其他的数据，所以，即使你上面的式子，确实是需要走的所有次数，但是，但是！！!它和数据总个数，还扯不上关系，所以，我们必须，要想办法，扯上关系

那么我们又知道，对于时间复杂度而言，是不是O（N）中的N就是，这段代码一共要运行多少次，那么对于我们的向下调整算法而言，因为它的本质还是个数组，所以最极端的情况下，它是不是就要将数组内的所有数据都给遍历一遍，那么就是要运行2^（h）-1次呢？因为我们经过上面的推理，知道满二叉树中，一共是有2^（h）-1个节点的。

所以，就是n = 2^（h） − 1.

我们再转换一下，就是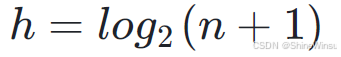

但是呢，我们又知道，实际上，最极端的情况，是要走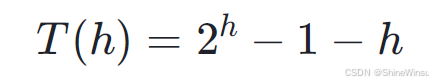次的，所以，我们再把上面的两个公式代入，就得到了：

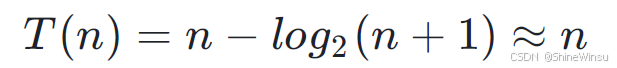
上面的约等于是根据大O渐进法得来的。

总结一下逻辑链

1. 堆是完全二叉树，用满二叉树的 "高度 h" 和 "节点数 n" 建立关系：n=2h−1，进而得到 h=log2​(n+1)。
2. 分析 "向下调整" 最极端的执行次数，得到关于 h 的表达式 T(h)=2h−1−h。
3. 把 h 替换为 n，得到 T(n)=n−log2​(n+1)。
4. 用大 O 忽略低阶的对数项，最终时间复杂度为 O(n)。

所以：💡 向下调整算法建堆时间复杂度为： O(n)

对于上面的手撕算法时间复杂度，大家最好还是理解一下，虽然这些前几年已经考烂了，但是呢？就怕旧事重提，不是吗诸位。回忆总想哭~一个人太孤独~~~~~~~~~~~

向上调整算法的时间复杂度：

那么我们上面分析完了向下调整算法的时间复杂度之后，我们接下来就要来思考思考，向上调整算法的时间复杂度了，这个时候，肯定有人说，嗯，向上和向下差不多，应该还是O（N），额，好想法，可惜就是错了。

由于说实话，确实向上和向下的计算时间复杂度的过程差不多，所以我们就直接放图供大家思考，计算过程和向下调整算法差不多的：

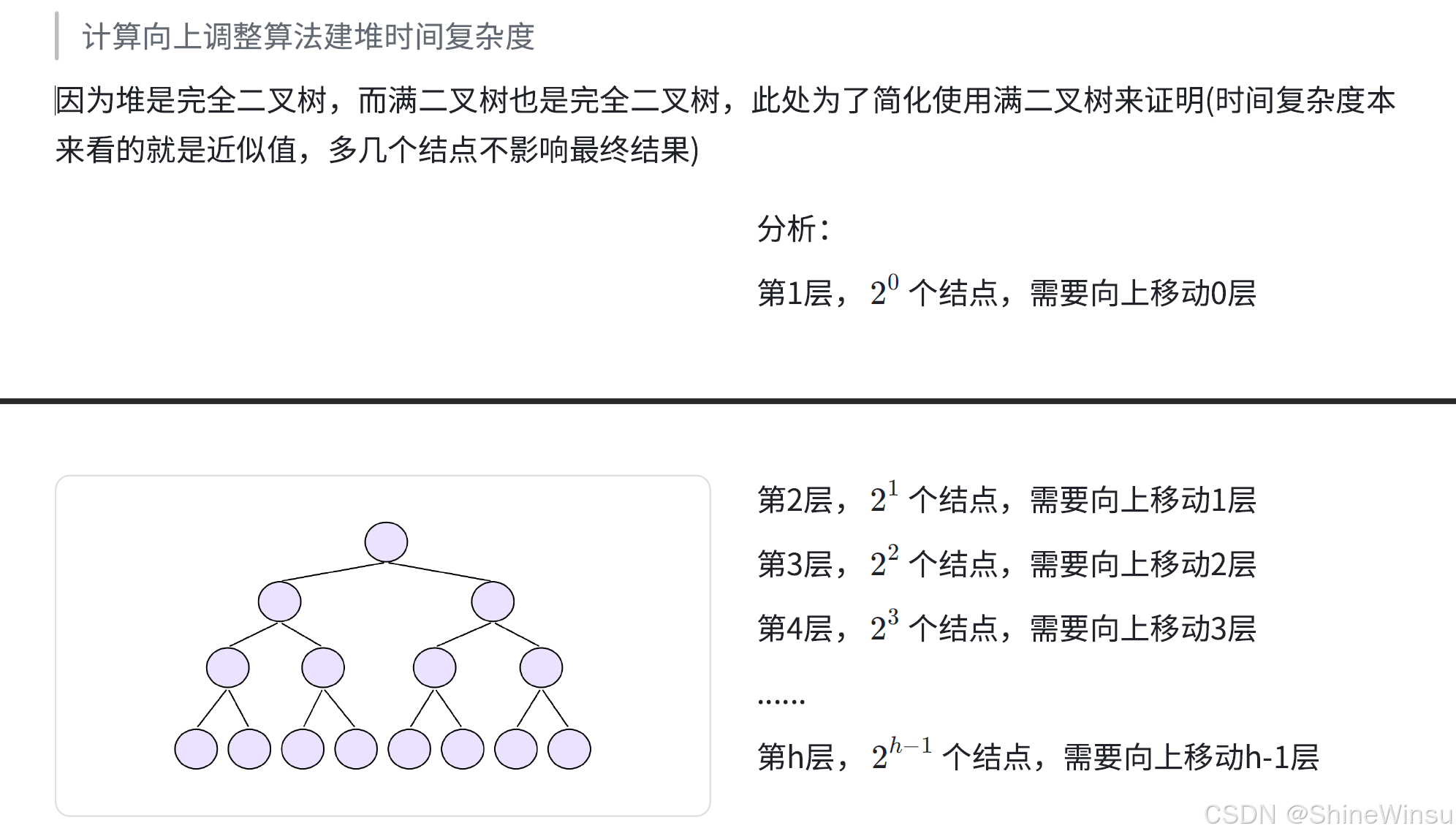
稍微详细解释一下：

一、背景：向上调整建堆的逻辑

向上调整建堆，是从数组的第二个元素开始（第一个元素可视为初始堆），依次将每个元素插入堆中，通过 "向上调整" 操作（和父节点比较、交换，直到满足堆性质），最终构建出完整的堆。

要分析时间复杂度，需计算所有元素向上调整的总操作次数，再看这个次数与堆的节点总数 n 的关系。

二、用 "满二叉树" 简化分析

堆是完全二叉树，为了简化推导，用满二叉树（完全二叉树的特殊情况，每层节点都满）来分析。满二叉树的高度为 h 时，节点总数 n=2h−1，反过来 h=log2​(n+1)。

三、分层分析 "向上调整" 的操作次数

满二叉树的每一层，节点数量和需要向上调整的层数有规律：

• 第 1 层：20 个节点（根节点），已在堆顶，向上调整 0 层；
• 第 2 层：21 个节点，最多需要向上调整 1 层（到根节点的下一层）；
• 第 3 层：22 个节点，最多需要向上调整 2 层；
• ...
• 第 h 层：2h−1 个节点，最多需要向上调整 h−1 层（到根节点，共 h−1 层距离）。

四、计算总调整次数 T(h)

总调整次数是 "每层节点数 × 该层每个节点的调整层数" 的总和。根据上面的规律，总次数 T(h) 为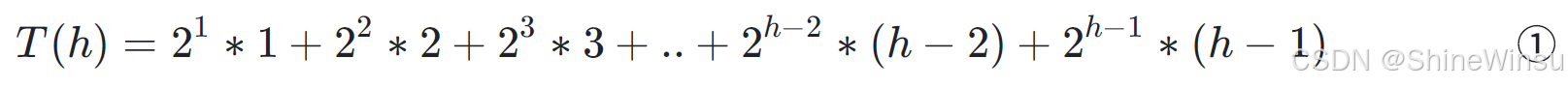：注意：第 1 层调整次数为 0，所以从第 2 层开始计算，即 21 对应第 2 层）

五、用 "错位相减" 求等比数列和

为了简化 T(h)，用错位相减法（等比数列求和常用技巧）：

步骤 1：构造 2×T(h)

给 T(h) 两边乘 2，得到：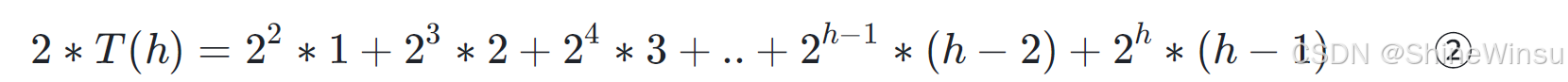

步骤 2：用 2×T(h)−T(h) 错位相减

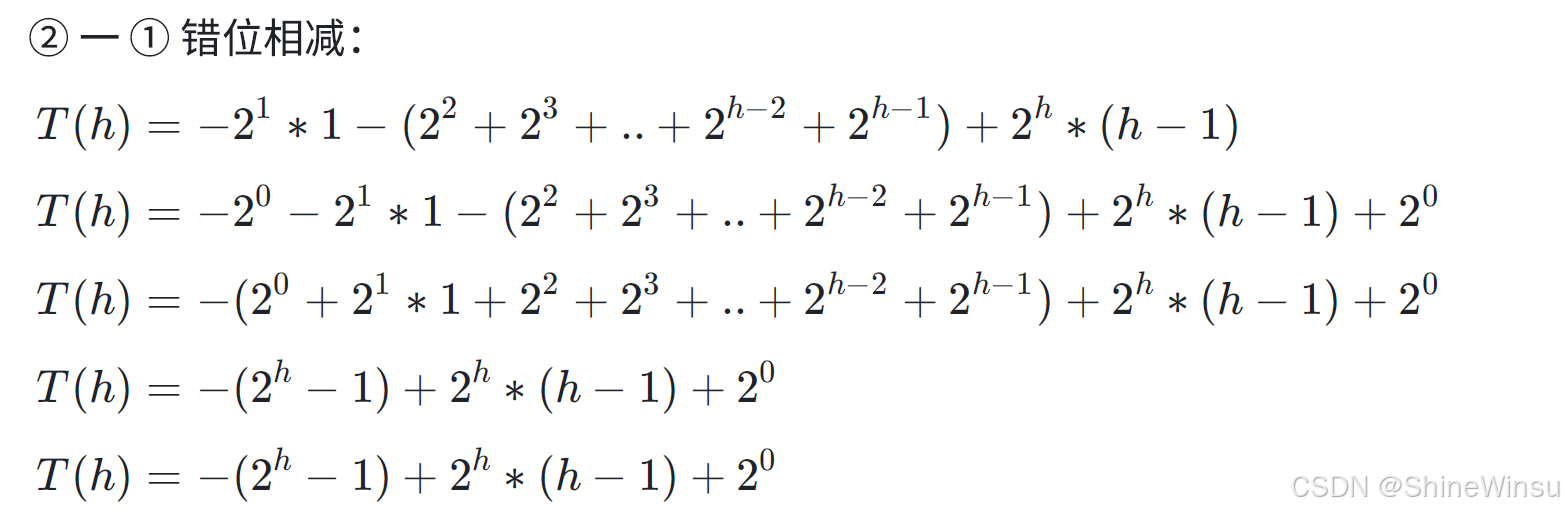
步骤 3：简化等比数列部分

其中 2^2+2^3+⋯+2^(h−1) 是等比数列（首项 2^2，公比 2，项数 h−2）。根据等比数列求和公式 S=q−1a1​^(qn−1)​（这里 a1​=2^2，q=2，n=h−2），可得：2^2+2^3+⋯+2^(h−1)=2−122(2h−2−1)​=2^h−4

步骤 4：代入并进一步简化 T(h)

把等比数列和代入 T(h)：T(h)​=−2+2h(h−1)−(2h−4)=−2+2h(h−1)−2h+4=2h(h−2)+2​

六、将 h 替换为 n，分析时间复杂度

由满二叉树性质，n=2h−1，即 2h=n+1；同时 h=log2​(n+1)。

将 2h=n+1 和 h=log2​(n+1) 代入 T(h)=2h(h−2)+2，得到：T(n)​=(n+1)(log2​(n+1)−2)+2=(n+1)log2​(n+1)−2(n+1)+2=(n+1)log2​(n+1)−2n​

大 O 渐进分析

大 O 关注 "增长最快的项"，忽略低阶项和常数：

• (n+1)log2(n+1) 是 "n*logn 级" 的项；
• −2n 是 "线性级" 项，增长远慢于 nlogn。

因此，当 n 很大时，T(n)≈O(n*logn)。

最终结论

向上调整算法建堆的时间复杂度为 O(nlogn)​。

简单来说：通过分析满二叉树每层的调整次数，用错位相减求出总次数的表达式，再结合大 O 忽略低阶项，得出时间复杂度是 O(nlogn)～

所以，💡 向上调整算法建堆时间复杂度为： O(n ∗ log 2 n)

所以，向上调整算法和向下调整算法，谁好谁坏，大家应该很明白了。

那么知道了之后，我们就可以讲一讲我们的方法二了

堆排序方法二：

这一个方法呢，其实算是对方法一的改进版，相对于方法一而言，它是将空间复杂度由O（N）转化为O（1），换句话来说，就是我们直接原地排序，不需要创建新空间。

那么怎么原地排序呢？其实我们知道，堆的本质，就是一个数组，而我们要进行排序的，是不是也是一个无序数组呢？错，谁说是数组了，我说的，咳咳咳，就是数组啦。

嘿嘿，毕竟除了数组，我们又有什么方法能够去连续的存储数据呢。

那么，既然我们要排序的数据，本身就是一个无序数组，那么那么，我们要想利用堆排序，是不是就能直接先把我们要排序的无序数组，转换为一个堆呢？很明显，可以的

同时，我们要知道：

升序，建大堆
降序，建小堆

至于原因？上面有的啦。

然后就是，我们要选用什么方法去建堆呢？大家这个时候可不要还说什么不知道，上面的向上调整算法和向下调整算法的时间复杂度，可不是白分析的，很明显，我们要用向下调整算法，去建堆。

那么这个时候，我们要怎么借助向下调整算法去进行建堆呢？换句话来说就是，我们要怎么通过向下调整算法去将原本的待排序、非堆的数组，转换为堆数组呢？

其实思路也很简单，本质上还是要去对原本的待排序、非堆的数组进行向下调整算法，因为我们知道，向下调整算法是从父节点开始向下进行判断以及调整的，那么我们想要将一个数组转换为堆数组，无论这么说，都得将数组的每一个父节点都进行一次向下调整算法吧，也就是，我们要对原本的待排序、非堆的数组的每一个父节点进行向下调整算法的判断，这样子将每个父节点都遍历之后，我们的堆数组，也就能够顺利实现了。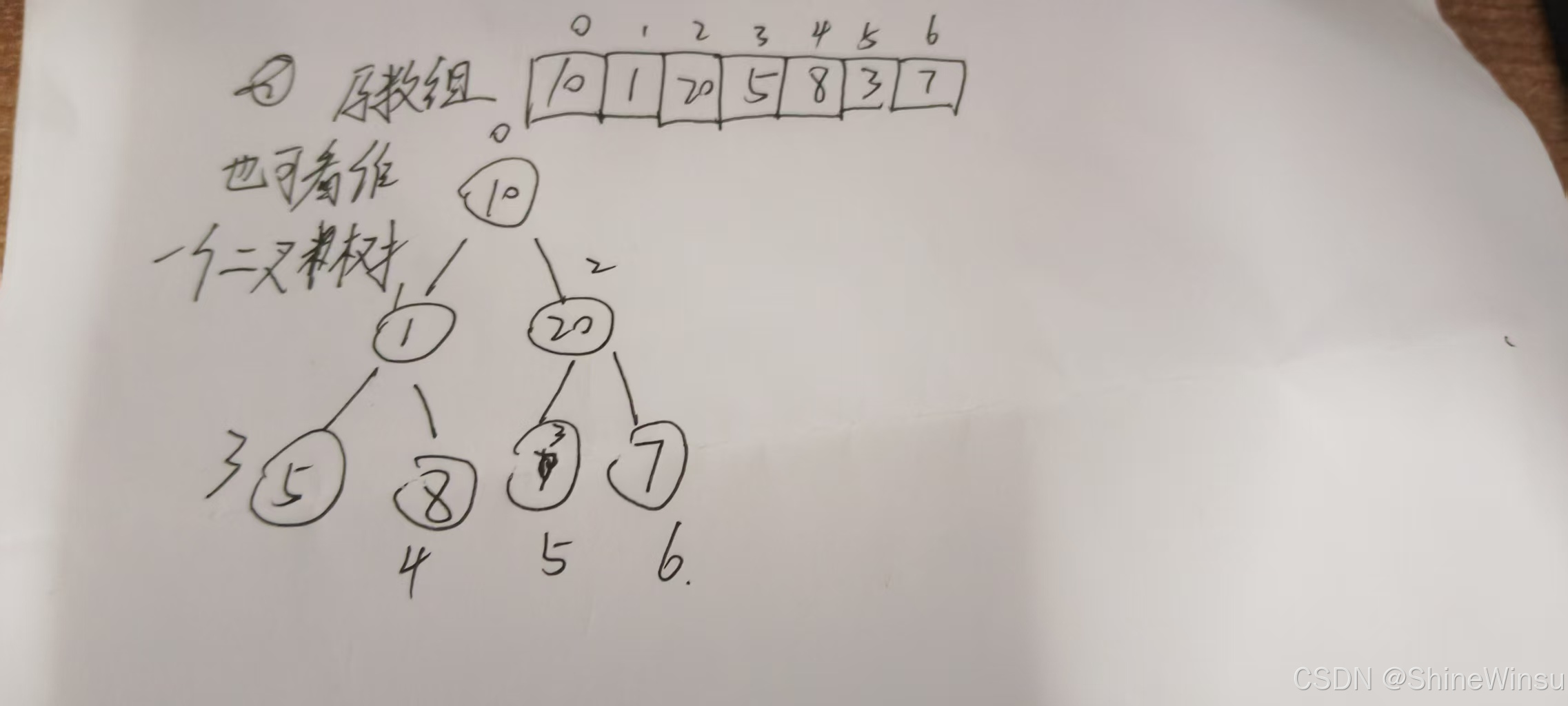

那么，我们要从原数组（非堆）的根节点进行，还是从哪个父节点开始呢？答案是，我们要从原二叉树的第一个非叶子节点开始，也就是最后一个父节点开始，然后依次递减，这个是为什么呢？

一、堆的核心概念与 "向下调整" 的作用

1. 堆的定义

堆是完全二叉树，同时满足 "堆性质"：

• 大根堆：每个父节点的值 ≥ 子节点的值；
• 小根堆：每个父节点的值 ≤ 子节点的值。完全二叉树可以用数组高效存储（父节点索引为 i，左子节点索引为 2i+1，右子节点索引为 2i+2）。

2. 向下调整算法的作用

当一个节点不满足 "堆性质" 时，向下调整会让以该节点为根的子树重新满足堆的性质。具体操作是：将当前节点与子节点比较，若不满足堆性质，就和 "较大（大根堆）/ 较小（小根堆）" 的子节点交换，然后递归（或循环）对交换后的子节点继续调整，直到满足堆性质或到达叶子节点。

二、"从最后一个父节点开始建堆" 的底层逻辑

要把普通数组（非堆结构）转换成堆，需要对每个父节点 执行 "向下调整"。但调整的顺序非常关键，原因是：向下调整的前提是「子树已经是堆」。如果子树不是堆，向下调整无法保证调整后整个子树满足堆性质。

三、如何找到 "最后一个父节点"？

完全二叉树中，节点总数为 n 时，父节点的索引范围是 0 到 ⌊2n​⌋−1（向下取整）。

• 例如图片中数组有 7 个元素（n=7），则 ⌊27⌋−1=3−1=2，所以最后一个父节点的索引是 2（对应数组中值为 20 的元素）。

四、建堆的具体步骤（以大根堆为例，数组 [10,1,20,5,8,3,7]）

数组索引与元素对应：index: 0→10, 1→1, 2→20, 3→5, 4→8, 5→3, 6→7，对应的完全二叉树结构如下（每层节点分布）：

• 第 0 层（根）：10
• 第 1 层：1（左子）、20（右子）
• 第 2 层：5（1的左子）、8（1的右子）、3（20的左子）、7（20的右子）

步骤 1：处理最后一个父节点（索引 2，值为 20）

• 它的左子节点索引 2×2+1=5（值为 3），右子节点索引 2×2+2=6（值为 7）。
• 大根堆要求父节点 ≥ 子节点，20≥3 且 20≥7，所以该子树已经是大根堆，无需调整。

步骤 2：处理前一个父节点（索引 1，值为 1）

• 左子节点索引 2×1+1=3（值为 5），右子节点索引 2×1+2=4（值为 8）。
• 大根堆要求父节点 ≥ 子节点，但 1<5 且 1<8，不满足堆性质。
• 选择较大的子节点 （8）与当前节点（1）交换，交换后数组变为：[10,8,20,5,1,3,7]。
• 交换后，检查交换后的子节点（原父节点 1 现在在索引 4）：它是叶子节点（没有子节点），所以调整结束。此时，以索引 1 为根的子树（包含 8、5、1）成为大根堆。

步骤 3：处理根节点（索引 0，值为 10）

• 左子节点索引 2×0+1=1（值为 8），右子节点索引 2×0+2=2（值为 20）。
• 大根堆要求父节点 ≥ 子节点，但 10<20，不满足堆性质。
• 选择较大的子节点 （20）与当前节点（10）交换，交换后数组变为：[20,8,10,5,1,3,7]。
• 交换后，检查交换后的子节点（原根节点 10 现在在索引 2）：它的左子节点索引 2×2+1=5（值为 3），右子节点索引 2×2+2=6（值为 7）。10≥3 且 10≥7，所以该子树已是大根堆，调整结束。

五、总结

用 "向下调整算法建堆" 的核心是：利用「子树已为堆」的前提，从最后一个父节点开始，从下往上、从右到左依次调整每个父节点，确保每一步调整时，子树已经满足堆性质，最终让整个数组（完全二叉树）成为堆。这种方式既保证了堆的正确性，又实现了高效的时间复杂度。

所以，我们要先通过向下调整算法去将原数组进行建堆，而且是要从最后一个父节点开始，并且依次递减，遍历原数组（二叉树）的所有父节点，再加上我们已经知道了最后一个父节点的下标是多少，即（n-1-1）/2，所以，我们的建堆代码，也就得到了：

// 交换两个元素
void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

// 向下调整算法（大根堆）
// 参数：a-数组，n-数组元素个数，parent-需要调整的父节点索引
void AdjustDown(int* a, int n, int parent)
{
    assert(a);
    
    // 先假设左孩子是较大的孩子
    int child = parent * 2 + 1;
    
    while (child < n)
    {
        // 如果右孩子存在且右孩子大于左孩子，则选择右孩子
        if (child + 1 < n && a[child + 1] > a[child])
        {
            child++;
        }
        
        // 如果子节点大于父节点，则交换
        if (a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            // 继续向下调整
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            // 满足堆的性质，调整结束
            break;
        }
    }
}

// 在原数组上直接构建大根堆（时间复杂度O(N)）
void BuildHeap(int* a, int n)
{
    assert(a && n >= 0);
    
    // 从最后一个父节点开始，依次向上调整每个父节点
    // 最后一个父节点的索引：(n-1-1)/2  等价于 (n/2 - 1)（整数除法）
    for (int i = (n - 1 - 1) / 2; i >= 0; --i)
    {
        AdjustDown(a, n, i);
    }
}

示例图如下：

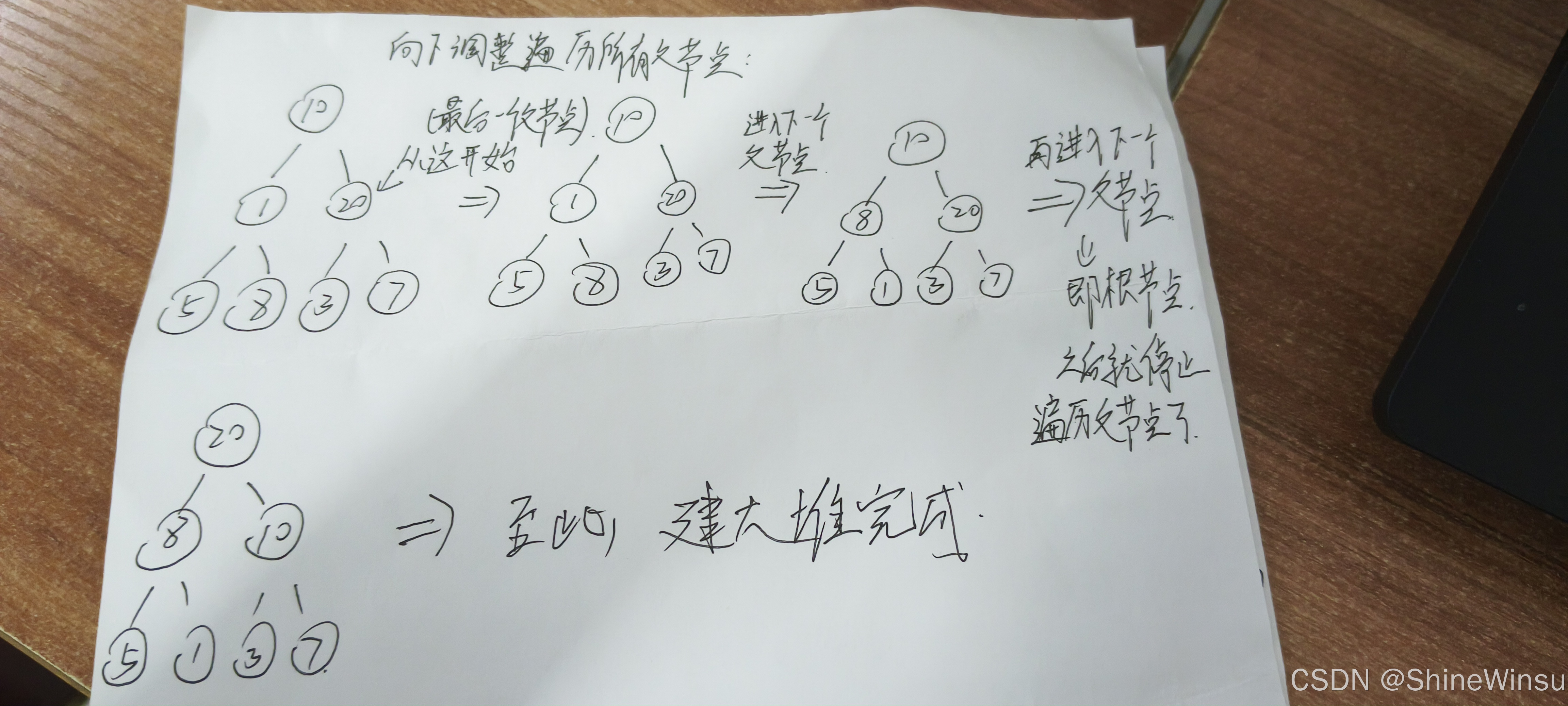
那么，在我们的方法一，我们是利用hptop函数去进行数据的取出以及存储进新数组中，那么在我们的方法二中，我们就是要，直接在我们要排序的数组中，直接进行堆排序：

我来说一下这个方法的思路，其实这个方法的思路也挺好理解的，就是对我们的hptop函数进行一些改造。

我们知道，我们想要进行堆排序，是不是其实就是要得到根节点的数据，而且无论你是升序还是降序，其实都是将每次形成的堆的根节点的数据给丢到数组后面去的，从数组的最后一个不断往前存储，这个大家结合方法一，应该就能够理解了。

那么，如果我们想要在数组里原地堆排序，是不是就相当于，要直接在我们的待排序数组中进行hptop函数呢，偶哟，好难搞哦，这要怎么实现呢？

其实和上篇博客讲的hptop函数差不多，我们依旧是要对已经形成的堆数组，进行首尾数据交换，然后再尾删一下，然后再继续进行操作，直到把堆数组删的没有数据了，这个时候，我们才停止循环。

相较于hptop不同的是，我们是不取出堆顶元素的，是直接就一直尾删加调整。

那么这个时候，大家肯定就好奇了，wdf，那怎么能够在原数组上直接堆排序呢？

首先，我们要定义一个指针end，然后这个end最开始是指向堆数组的最后一个数据，也就是二叉树的最后一个节点，之后我们交换头尾数据，然后进行尾删，尾删和顺序表尾删类似，我们将end指针--，代表我们将end指针前移一下，不管原本的最后一个数据了，尾删之后我们再借助向下调整算法去将形成的新二叉树转换为正确的堆，然后就一直重复上述操作，直到end变为0了，这时候就代表没有数据可以再排序了，毕竟end指针都运动到0了，就代表明面上的数组只有一个数据了，那么这个时候肯定就无法进行向下调整了

OK？大家可能还是不懂，没事，诶，大家看我下图的演示，大家就明白了，

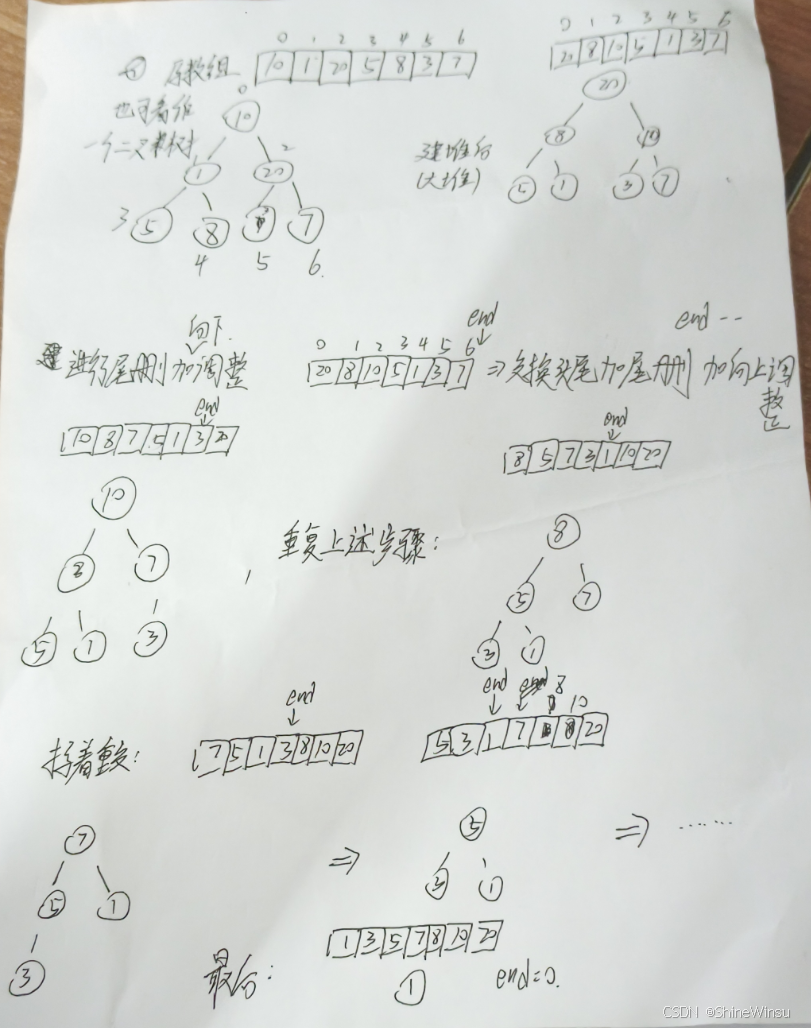
如上，这样子大家应该就能明白了，诶，我上面好像没有将头尾数据交换表示出来，咳咳咳，没事，我相信大家能够理解，这边说明一下，我们的end--并不算是对数组最后一个数据给直接除去，我们只是把原本end指向的那一个数据给忽略了而已。

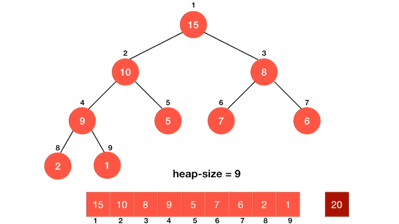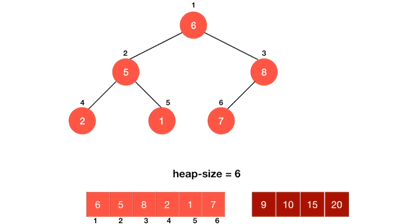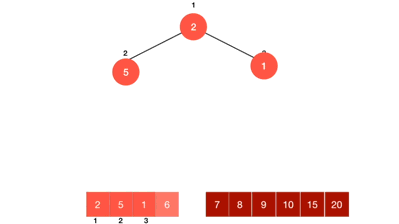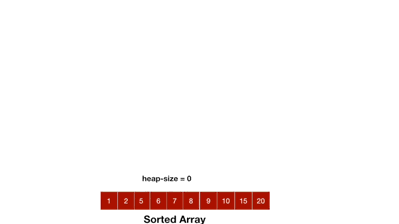或者大家也可以看这个动图理解理解

由此，我们的堆排序方法二，就讲的差不多了，我们看完整代码：

#include <stdio.h>
#include <assert.h>

// 交换两个元素
void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

// 向下调整算法（大根堆）
void AdjustDown(int* a, int n, int parent)
{
    assert(a);
    
    // 假设左孩子为较大的孩子
    int child = parent * 2 + 1;
    
    while (child < n)
    {
        // 右孩子存在且大于左孩子，则选择右孩子
        if (child + 1 < n && a[child + 1] > a[child])
        {
            child++;
        }
        
        // 子节点大于父节点则交换
        if (a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break; // 满足堆性质，停止调整
        }
    }
}

// 堆排序（升序排序，使用大根堆）
// 时间复杂度：O(N log N)
void HeapSort(int* a, int n)
{
    assert(a && n >= 0);
    if (n <= 1) return; // 边界条件处理
    
    // 1. 直接在原数组上构建大根堆，时间复杂度 O(N)
    for (int i = (n - 1 - 1) / 2; i >= 0; --i)
    {
        AdjustDown(a, n, i);
    }
    
    // 2. 排序过程，时间复杂度 O(N log N)
    int end = n - 1;
    while (end > 0)
    {
        // 交换堆顶（最大值）和当前末尾元素
        Swap(&a[0], &a[end]);
        
        // 调整剩余元素为大根堆（排除已排序的末尾元素）
        AdjustDown(a, end, 0);
        
        // 缩小排序范围
        --end;
    }
}

// 打印数组
void PrintArray(int* a, int n)
{
    for (int i = 0; i < n; ++i)
    {
        printf("%d ", a[i]);
    }
    printf("\n");
}

// 测试函数
int main()
{
    int a[] = {3, 1, 2, 5, 4, 6, 8, 7, 9};
    int n = sizeof(a) / sizeof(a[0]);
    
    printf("排序前: ");
    PrintArray(a, n);
    
    HeapSort(a, n);
    
    printf("排序后: ");
    PrintArray(a, n);
    
    return 0;
}

在这里，其实有个小细节，前面被忽略了，就是关于上面代码的end，我们知道，end的作用是指向堆数组的最后一个数据，同时与堆数组的头数据进行交换，然后执行end--，而堆数组的最后一个数据的下标是size-1。

那么，我们在交换了数据之后，理应是要对堆数组进行尾删，然后再用向下调整算法去将数组重新确立为堆，那么这个时候，我们对向下调整算法传入的堆数组长度就是end，而不是end-1，这是为什么呢？其实在我们将end传入向下调整算法时，就已经实现了对堆数组的尾删。

因为我们知道，end的初始值就是size-1，那么我们知道，实际上最开始的堆数组的数据个数是size，而在我们进行了将堆数组头尾元素交换了之后，我们将end直接传进向下调整算法中，那是不是就相当于我们认为新数组的数据个数只有end个，其实也就是size-1个，而这一步，不是正好符合了尾删了，即将最后一个数据给忽略掉。

而后我们再指向end--，即让end前移一个数据，那么其实就是类似上面的步骤了，由此重复。

将end初始化为size-1，既能够直接通过end指向堆数组的最后一个数据，又能在将end传进向下调整算法时代表忽略了最后一个数据，可以说，这个设计是非常巧妙的，也是第一遍敲代码时很难直接想到的。

1. 堆的基本概念与初始状态

堆是一种完全二叉树，分为 "大根堆"（父节点值 ≥ 子节点值）和 "小根堆"（父节点值 ≤ 子节点值）。堆排序通常基于大根堆实现（升序排序）。

假设我们有一个数组 arr，长度为 size。初始时，我们需要先将数组调整为大根堆（这一步是 "建堆" 过程，通常用 "向下调整算法" 从最后一个非叶子节点开始调整）。

2. end 的初始含义：指向堆的最后一个有效元素

end 的初始值被设为 size - 1，这是因为数组的下标从 0 开始，size - 1 正好是数组最后一个元素的下标 。此时，end 指向 "堆的最后一个有效数据"，整个堆的有效范围是 arr[0...end]（即包含所有 size 个元素）。

3. 堆顶与 end 元素交换："弹出" 最大值

大根堆的堆顶（arr[0]）是当前堆中的最大值 。堆排序的核心思想是：每次将堆顶的最大值与堆的最后一个元素交换，这样最大值就被 "放到了正确的位置"（数组末尾，后续不再参与堆的调整）。

此时，交换后有两个关键变化：

• 最大值被移动到 arr[end]（数组末尾，排序完成的部分）。
• 堆的 "有效范围" 需要缩小（因为 arr[end] 已经是最终值，不再属于堆的待调整部分）。

4. 传入 end 到向下调整算法：隐式实现 "尾删"

向下调整算法的作用是：在堆的结构被破坏后，重新调整堆为大根堆。

当我们把 end 传入向下调整算法时，算法的逻辑是只处理 arr[0...end - 1] 这个范围的元素 （因为数组是左闭右闭区间，end - 1 是新的 "最后一个待调整元素" 的下标）。这相当于：

• 忽略了 arr[end]（因为它已经是最大值，不需要再调整）。
• 堆的有效长度从 size 变成了 end（因为 end 初始是 size - 1，所以 end 的数值等于 "新的有效元素个数"）。

这一步隐式地完成了 "尾删" ------ 不需要真正删除数组元素，而是通过缩小向下调整的范围 ，让已排序的 arr[end] 不再参与堆的调整。

5. end--：迭代缩小堆的范围

交换并调整堆后，执行 end--，让 end 指向前一个元素（即 arr[end - 1]）。此时：

• 下一轮排序中，堆的有效范围变为 arr[0...end]（长度再次减 1）。
• 重复 "交换堆顶与 end 元素 → 传入 end 调整堆 → end--" 的过程，直到 end 缩小到 0（所有元素都排序完成）。

6. 设计的巧妙之处

将 end 初始化为 size - 1，同时利用 "向下调整算法的范围控制" 和 end--，实现了：

• 直接指向最后一个元素：方便堆顶与末尾元素交换。
• 隐式尾删：通过调整算法的范围，自然忽略已排序的末尾元素。
• 迭代一致性：每一轮的逻辑完全重复，代码简洁且高效。

通过 end 的这种设计，堆排序无需额外的空间删除元素，仅通过下标控制范围，就完成了 "排序 + 逐步固定最大值" 的过程，是空间复杂度优化和算法逻辑紧凑性的体现。

希望大家注意。

OK，至此，堆排序，大功告成。

TOP-K问题：

这个问题是这样的：

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

那么对于Top-K问题，我们第一时间能想到的最简单直接的方式就是排序，无论你是堆排序，还是快速排序，还是归并排序，都是可以的。

但是，大家有没有想过，如果要排序的数据是10000000000000000000000000000000个数据呢？那这个时候，还排序？怎么可能得嘞，排到猴年马月去，甚至可能数据都不能一下子全部加载到内存中。

那么，我们要用什么方法去解决呢？

最佳的方式就是用堆来解决，基本思路如下：
（1）用数据集合中前K个元素来建堆

• 前k个最大的元素，则建小堆
• 前k个最小的元素，则建大堆

（2）用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素，替换完需要重新调整二叉树（新数组）为堆，将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素

咱们把 TOP-K 问题的堆解法拆解得更细致，结合例子一步一步吃透每一个逻辑～

一、为什么用堆解决 TOP-K 问题？

当数据量极大 （比如 10 亿个数据），无法全部加载到内存时，直接排序（需要 O (N) 空间）不现实。而堆解法只需维护大小为 K 的堆，空间复杂度 O (K)，非常适合海量数据场景。

二、核心思路："建堆筛选" 的底层逻辑

1. 堆的类型选择：为什么 "前 K 大建小堆，前 K 小建大堆"？

这是整个算法的灵魂，关键在于堆顶的 "守门人" 角色：

• 找前 K 个最大元素→小堆 ：小堆的堆顶是堆中最小的元素。这个堆顶就像 "门槛"------ 只有比它大的元素，才有资格进入 "前 K 大" 的候选集合。例如：堆里已有 3 个较大元素，堆顶是其中最小的（比如 5）。如果新元素是 6（比 5 大），说明它比当前门槛高，应该替换堆顶，重新调整堆（保证新堆顶仍是当前堆里最小的）。最终堆里剩下的，就是所有元素中最大的 K 个。

• 找前 K 个最小元素→大堆 ：大堆的堆顶是堆中最大的元素。这个堆顶是 "门槛"------ 只有比它小的元素，才有资格进入 "前 K 小" 的候选集合。例如：堆里已有 3 个较小元素，堆顶是其中最大的（比如 5）。如果新元素是 3（比 5 小），说明它比当前门槛低，应该替换堆顶，重新调整堆（保证新堆顶仍是当前堆里最大的）。最终堆里剩下的，就是所有元素中最小的 K 个。

2. 两步走流程（以 "前 K 大，建小堆" 为例）

假设总数据量为 N，目标是找出最大的 K 个元素：

• 第一步：用前 K 个元素建小堆这一步是为了先确定一个初始的 "候选集合"，堆顶是这个集合中最小的元素（初始门槛）。

• 第二步：用剩余 N-K 个元素筛选堆顶逐个遍历剩下的元素，每个元素都和堆顶（当前门槛）比较：

  • 若元素 > 堆顶：说明它比当前门槛高，替换堆顶，再调整堆（保持小堆性质，更新门槛）。
  • 若元素 ≤ 堆顶：说明它不够资格进入候选集合，直接跳过。遍历结束后，堆中剩下的 K 个元素就是最终结果。

三、例子详解：找数组 [5,9,3,7,1,8,2,6] 的前 3 大元素（K=3）

步骤 1：取前 3 个元素，建小堆（初始候选集合）

前 3 个元素是5,9,3，建小堆的过程：小堆要求 "父节点 ≤ 子节点"，所以需要调整这 3 个元素的位置：

• 初始数组：[5,9,3]（对应完全二叉树：根 5，左子 9，右子 3）

• 调整：根 5 的右子 3 比它小，交换后变成[3,9,5]，此时满足小堆性质（3≤9 且 3≤5）。堆结构如下（堆顶是 3，即当前候选集合中最小的元素）：

      3  ← 堆顶（门槛：当前3个候选中最小的）
     / \
    9   5

步骤 2：遍历剩余元素（7,1,8,2,6），逐个筛选

剩余元素共 5 个（N-K=8-3=5），逐个与堆顶（门槛）比较：

1. 处理元素 7：

   • 7 > 堆顶 3 → 有资格进入候选集合。

   • 替换堆顶：堆变为[7,9,5]。

   • 调整小堆：此时 7 的左子 9 和右子 5 都比它大，不满足小堆性质（7>5），需要交换 7 和 5，调整后堆为[5,9,7]。新堆顶是 5（更新门槛：当前 3 个候选中最小的是 5）：

     plaintext

         5  ← 新门槛
        / \
       9   7

2. 处理元素 1：

   • 1 < 堆顶 5 → 不够资格，直接跳过。堆不变。

3. 处理元素 8：

   • 8 > 堆顶 5 → 有资格进入候选集合。

   • 替换堆顶：堆变为[8,9,7]。

   • 调整小堆：8 的左子 9 和右子 7 都比它小（8>7），交换 8 和 7，调整后堆为[7,9,8]。新堆顶是 7（更新门槛：当前 3 个候选中最小的是 7）：

         7  ← 新门槛
        / \
       9   8

4. 处理元素 2：

   • 2 < 堆顶 7 → 不够资格，直接跳过。堆不变。

5. 处理元素 6：

   • 6 < 堆顶 7 → 不够资格，直接跳过。堆不变。

步骤 3：最终结果

堆中剩下的 3 个元素是7,9,8，这正是原数组中最大的 3 个元素（9、8、7）。

四、关键逻辑再强调

• 堆的大小始终是 K：无论怎么替换和调整，堆中永远只保留 K 个元素，空间效率极高。
• 堆顶的 "门槛" 作用：小堆的堆顶是当前候选中最小的（确保比它大的才能进入），大堆的堆顶是当前候选中最大的（确保比它小的才能进入）。
• **为什么不建大堆找前 K 大？**假设建大堆，堆顶是最大元素。此时剩下的元素中如果有比其他候选小的元素，无法有效筛选（大堆顶是最大值，其他元素比它小，但可能比候选中的其他元素大），会导致最终结果错误。

通过这种方式，只需 O (K) 空间和 O (N log K) 时间，就能在海量数据中高效找到前 K 个最大 / 最小元素，这就是堆在 TOP-K 问题中的核心价值～

大家看了上面的详细解释之后，是不是就明白了很多，是的，这就是我们topk问题的解法，那么相信大家此时肯定想要自己去实现一下，那么我这里就给大家提供一个代码，供大家试验。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// 向下调整函数，构建小根堆
void AdjustDown(int* arr, int size, int parent) {
    int child = parent * 2 + 1;
    while (child < size) {
        // 找较小的孩子
        if (child + 1 < size && arr[child + 1] < arr[child]) {
            child++;
        }
        // 如果孩子比父节点小，交换
        if (arr[child] < arr[parent]) {
            int temp = arr[child];
            arr[child] = arr[parent];
            arr[parent] = temp;
            parent = child;
            child = parent * 2 + 1;
        } else {
            break;
        }
    }
}

// 生成数据
void CreateNDate() {
    // 造数据
    int n = 100000;
    srand(time(0));
    const char* file = "data.txt";
    FILE* fin = fopen(file, "w");
    if (fin == NULL) {
        perror("fopen error");
        return;
    }
    for (int i = 0; i < n; ++i) {
        int x = (rand() + i) % 1000000;
        fprintf(fin, "%d\n", x);
    }
    fclose(fin);
}

// 解决 TOP-K 问题，找出最大的 K 个元素
void topk() {
    printf("请输入 k：>");
    int k = 0;
    scanf("%d", &k);
    const char* file = "data.txt";
    FILE* fout = fopen(file, "r");
    if (fout == NULL) {
        perror("fopen error");
        return;
    }
    int* minheap = (int*)malloc(sizeof(int) * k);
    if (minheap == NULL) {
        perror("malloc error");
        fclose(fout);
        return;
    }
    for (int i = 0; i < k; i++) {
        fscanf(fout, "%d", &minheap[i]);
    }
    // 建 k 个数据的小堆
    for (int i = (k - 1 - 1) / 2; i >= 0; i--) {
        AdjustDown(minheap, k, i);
    }
    int x = 0;
    while (fscanf(fout, "%d", &x) != EOF) {
        // 读取剩余数据，比堆顶的值大，就替换进堆
        if (x > minheap[0]) {
            minheap[0] = x;
            AdjustDown(minheap, k, 0);
        }
    }
    for (int i = 0; i < k; i++) {
        printf("%d ", minheap[i]);
    }
    printf("\n");
    fclose(fout);
    free(minheap);
}

int main() {
    CreateNDate();
    topk();
    return 0;
}

至此，topk问题大功告成。

结语：从堆的逻辑出发，看见算法世界的 "取舍与适配"

敲完最后一行代码，看着屏幕上堆排序的测试结果和 TOP-K 问题的输出数据，忽然有种 "走完一段小旅程" 的感觉。从开篇回忆堆的基础特性，到一点点拆解堆排序的两种实现方式，再到深入剖析 TOP-K 问题的海量数据解决方案，每一步都像是在 "解锁算法的密码"------ 那些看似复杂的逻辑背后，藏着的其实是对 "效率" 与 "场景" 的精准权衡。

还记得刚讲堆排序方法一时，我们需要额外创建一个堆结构来存储数据，当时我调侃 "这个方法现实中 dog 都不用"，并非是贬低它，而是想让大家直观感受到 "算法优化的必要性"。方法一的价值，在于它帮我们搭建了 "堆与排序" 之间的桥梁：通过 HPush 插入元素建堆，再通过 HPTop+HPPop 取出最值，这个过程就像 "用手把无序的珠子一颗颗按大小排列"，虽然直观，但额外的空间开销让它在大数据场景下显得笨重。而方法二的 "原地建堆"，则像是 "在原有的珠子堆里直接整理"------ 从最后一个父节点开始向下调整，利用向下调整算法 O (N) 的时间复杂度，把额外空间压缩到 O (1)，这种 "就地取材" 的思路，正是算法设计中 "空间与时间平衡" 的经典体现。

很多同学在学完两种方法后会问："既然方法二这么好，为什么还要学方法一？" 其实答案很简单：理解 "不完美" 的解法，才能更懂 "完美" 解法的巧妙。就像我们知道了 "向上调整建堆时间复杂度是 O (N log N)"，才会明白 "向下调整建堆 O (N)" 的优势；知道了 "额外空间的开销"，才会珍惜 "原地排序" 的高效。这种对比学习的过程，比单纯记住代码片段重要得多 ------ 毕竟未来遇到新问题时，没人会直接给你 "最优解"，但你可以通过对比不同思路的优劣，找到最适合当前场景的方案。

而 TOP-K 问题的讲解，更像是给堆的 "能力边界" 打开了一扇新窗。在讲这个问题之前，我特意强调 "当数据量大到无法全部加载进内存时"，就是想让大家跳出 "必须排序所有数据" 的思维定式。用一个大小为 K 的小堆（找前 K 大）或大堆（找前 K 小）做 "筛选器"，只保留比堆顶更有资格的元素，这种 "抓重点" 的思路，完美契合了海量数据场景的需求。我还记得第一次用这个方法处理 100 万条数据时的惊喜：原本需要几分钟才能排完序的代码，用堆筛选后几秒钟就出了结果。那种 "用对算法就能事半功倍" 的感受，或许就是学习算法的最大乐趣之一。

其实，堆的应用远不止于此。在后续的学习中，你会发现它是 "优先队列" 的核心实现方式 ------ 比如操作系统中优先处理高优先级的任务，比如电商平台中实时展示销量 TOP10 的商品，比如日志分析中快速定位高频错误信息，这些场景的底层逻辑，都离不开 "堆顶是最值""调整堆维持性质" 的核心思想。就像我们学会了 "用积木搭房子"，之后无论是搭城堡还是搭桥梁，核心的拼接技巧都是相通的。你今天掌握的 "向下调整""原地建堆"，未来都会成为解决更复杂问题的 "基础工具"。

当然，我也知道，文中那些数学推导 ------ 比如向下调整算法时间复杂度的错位相减，比如向上调整建堆 O (N log N) 的推导 ------ 可能会让一些同学感到头疼。我当初学的时候，也曾对着 "满二叉树节点数 2^h -1" 的公式反复演算，甚至怀疑 "这些推导真的有用吗？" 直到后来遇到需要优化算法效率的场景，才明白这些推导不是 "纸上谈兵"：知道了向下调整比向上调整高效，就能在建堆时果断选择前者；知道了 TOP-K 的时间复杂度是 O (N log K)，就能在面对百万级数据时，自信地放弃 "全量排序" 的思路。这些 "看不见的推导"，其实是帮我们在 "凭感觉选算法" 和 "靠理性选算法" 之间，搭建了一座桥梁。

写到这里，忽然想起刚开始学数据结构时的自己：对着 "堆" 的定义反复背诵，对着 "调整算法" 的代码逐行模仿，却总也搞不懂 "为什么要这么做"。直到后来亲手实现了堆排序，亲手用堆解决了一次 "找出班级前 10 名成绩" 的小问题，才真正理解了 "堆" 的价值。所以，如果你现在还觉得有些地方绕不过来，别着急 ------ 试着把代码敲一遍，试着用小数据量测试一遍，试着自己画一画堆的调整过程，很多困惑会在实践中慢慢解开。算法学习从来不是 "一次性学会" 的，而是 "在理解 - 实践 - 复盘" 中不断深化的过程。

最后，想跟大家说：堆排序与 TOP-K 问题，只是算法世界里的 "一小片风景"。未来你还会遇到树、图、哈希表等更多数据结构，还会遇到动态规划、贪心、回溯等更多算法思想。但无论学到哪里，请记得今天这份 "拆解问题" 的耐心 ------ 把复杂的逻辑拆成小模块，把难懂的推导拆成小步骤，把庞大的场景拆成小案例。就像我们今天用堆解决了排序和筛选的问题，未来也能用同样的思路，去解决更复杂的挑战。

希望这篇博客不仅能让你掌握堆排序和 TOP-K 的解法，更能让你感受到 "算法不是冰冷的代码，而是解决问题的智慧"。每一个算法的背后，都藏着对 "效率" 的追求，对 "场景" 的适配，对 "复杂问题简单化" 的思考。而这种思考能力，会比任何一个具体的算法知识点，都更能伴随你在编程的道路上走得更远。

期待下次见面时，我们能带着今天学到的 "堆思维"，去探索更广阔的技术世界。愿你在未来的学习中，既能啃下复杂的知识点，也能享受解决问题的乐趣；既能写出高效的代码，也能理解代码背后的逻辑。继续加油吧，每一个在算法世界里不断探索的学习者，都在朝着更专业、更从容的方向，稳步前行～

诸君共勉，我们下一篇，链式二叉树，再见。