深度学习：从零开始手搓一个浅层神经网络（Single Hidden Layer Neural Network）

本文带你一步步用 Python 实现一个最基础的神经网络模型，理解前向传播、反向传播、梯度下降等核心概念，真正"动手"掌握深度学习的本质。

---

🔍 一、引言：为什么我们要自己写神经网络？

在今天，我们有 TensorFlow、PyTorch 等强大的框架可以快速构建复杂的模型。但如果你只是初学者，或者想深入理解神经网络的内部机制，亲手实现一个简单的神经网络是绝佳的学习方式。

本篇博客将带你从头到尾实现一个含有一个隐藏层的神经网络，用于解决二维平面数据分类问题（如非线性可分的数据）。我们将使用 NumPy 和 Matplotlib 手动完成所有计算，不依赖任何高级框架。

---

🧩 二、整体架构概览

我们构建的是如下结构的神经网络：

输入层 (2个特征) → 隐藏层 (n_h个神经元) → 输出层 (1个神经元)
       ↓                  ↓                   ↓
     x₁, x₂             tanh(Z₁)           tanh(Z₂)

• 输入：每个样本有两个特征（横纵坐标）

• 隐藏层：n_h 个神经元，激活函数为 tanh

• 输出层：1 个神经元，激活函数也为 tanh（也可改为 sigmoid，这里为了简化）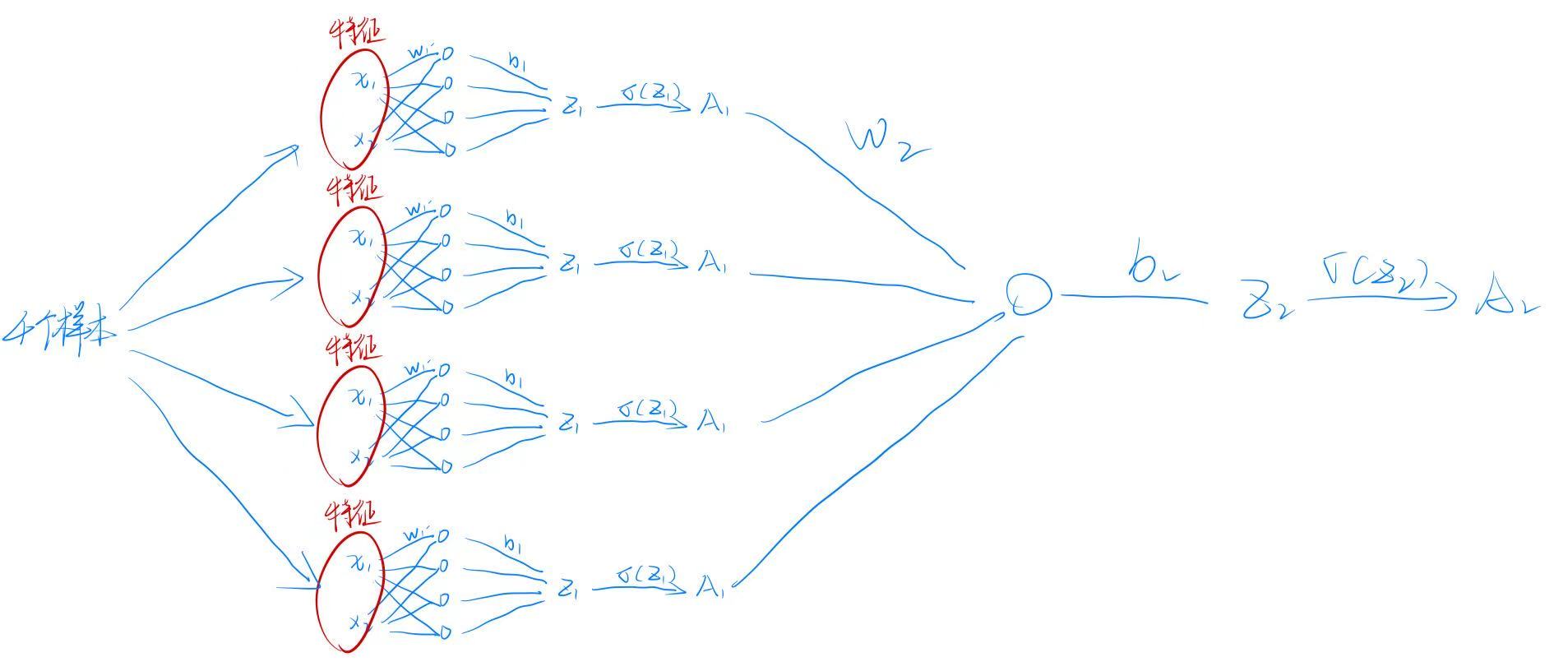

  

（注：图中红色椭圆表示输入特征，蓝色箭头表示权重连接）

---

📦 三、环境准备与数据加载

import matplotlib
matplotlib.use('TkAgg')  # 如果有GUI支持
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.linear_model

from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
from testCases import *

np.random.seed(1)

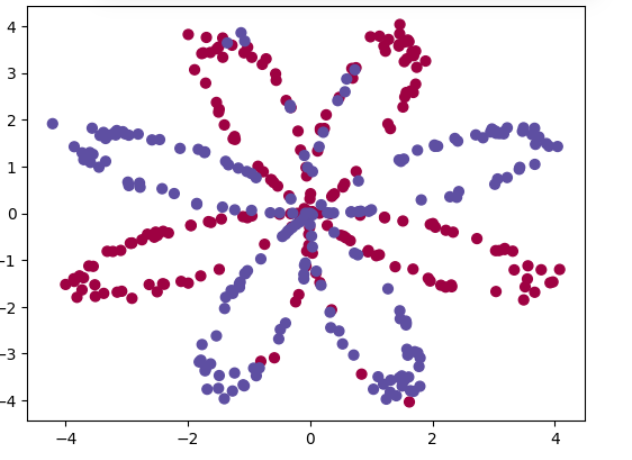
X, Y = load_planar_dataset()

plt.scatter(X[0,:], X[1,:], c=Y.ravel(), s=40, cmap=plt.cm.Spectral)
plt.title("原始数据分布")
plt.show()

✅ 解释：

• load_planar_dataset() 是一个辅助函数，生成了带有标签的二维点集（通常是环形或花形数据，非线性可分）。
• 使用 scatter 可视化数据，可以看到颜色不同的两类点无法用直线分开。
• 这正是神经网络发挥作用的地方！

---

🛠️ 四、参数初始化

def initialize_parameters(n_x, n_h, n_y):
    np.random.seed(2)
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))

    parameters = {
        "W1": W1,
        "b1": b1,
        "W2": W2,
        "b2": b2
    }
    return parameters

✅ 说明：

• n_x: 输入维度（这里是 2）
• n_h: 隐藏层神经元数量（可调参）
• n_y: 输出维度（这里是 1）
• 权重 W 用小随机数初始化（乘以 0.01），防止梯度爆炸
• 偏置 b 初始为 0

---

⏭️ 五、前向传播（Forward Propagation）

def forward_propagation(X, parameters):
    m = X.shape[1]
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = np.tanh(Z2)

    cache = {"Z1": Z1, "A1": A1, "Z2": Z2, "A2": A2}
    return A2, cache

✅ 数学公式：

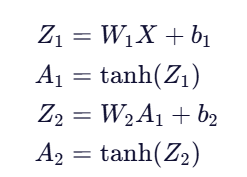
• A2 是最终输出，代表对每个样本的预测值
• cache 保存中间变量，供后续反向传播使用

---

🔢 六、损失函数计算

def compute_cost(A2, Y, parameters):
    m = Y.shape[1]
    logprobs = np.multiply(np.log(A2), Y) + np.multiply(1 - Y, np.log(1 - A2))
    cost = -np.sum(logprobs) / m
    return cost

✅ 注意：

• 这里用了 二元交叉熵损失函数（Binary Cross-Entropy），适用于二分类任务
• 但注意：由于我们用了 tanh 作为激活函数，其输出范围是 [-1, 1]，而标准交叉熵要求 [0,1]，所以严格来说应该改用 sigmoid 或调整标签
• 实际上，在这个练习中，我们更关注流程而非精确性，因此仍可用此形式

---

🔁 七、反向传播（Backward Propagation）

def backward_promagation(parameters, cache, X, Y):
    m = X.shape[1]
    W1 = parameters['W1']
    W2 = parameters['W2']
    A1 = cache['A1']
    A2 = cache['A2']

    dZ2 = A2 - Y
    dW2 = (1 / m) * np.dot(dZ2, A1.T)
    db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
    dW1 = (1 / m) * np.dot(dZ1, X.T)
    db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)

    grads = {
        "dW1": dW1,
        "db1": db1,
        "dW2": dW2,
        "db2": db2
    }
    return grads

✅ 数学推导简述：

• 
• 
• （因为 ）

---

⬇️ 八、参数更新（梯度下降）

def update_parameters(parameters, grads, learning_rate=1.2):
    W1 = parameters['W1'] - learning_rate * grads['dW1']
    b1 = parameters['b1'] - learning_rate * grads['db1']
    W2 = parameters['W2'] - learning_rate * grads['dW2']
    b2 = parameters['b2'] - learning_rate * grads['db2']

    parameters = {
        "W1": W1,
        "b1": b1,
        "W2": W2,
        "b2": b2
    }
    return parameters

✅ 说明：

• 使用标准梯度下降法更新参数
• 学习率设为 1.2，可根据训练情况调整

---

🔄 九、整合训练流程

def nn_model(X, Y, n_h, num_iterations=10000, print_cost=False):
    np.random.seed(3)
    n_x = X.shape[0]
    n_y = Y.shape[0]

    parameters = initialize_parameters(n_x, n_h, n_y)

    for i in range(num_iterations):
        A2, cache = forward_propagation(X, parameters)
        cost = compute_cost(A2, Y, parameters)
        grads = backward_promagation(parameters, cache, X, Y)
        parameters = update_parameters(parameters, grads)

        if print_cost and i % 1000 == 0:
            print(f"第 {i} 次迭代后，成本为: {cost}")

    return parameters

✅ 功能：

• 封装整个训练流程
• 多次迭代优化参数
• 打印成本变化趋势

---

🎯 十、测试与可视化

X_assess, Y_assess = nn_model_test_case()
parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False)

# 绘制决策边界
plot_decision_boundary(lambda x: predict(x, parameters), X, Y)
plt.title("训练后的决策边界")
plt.show()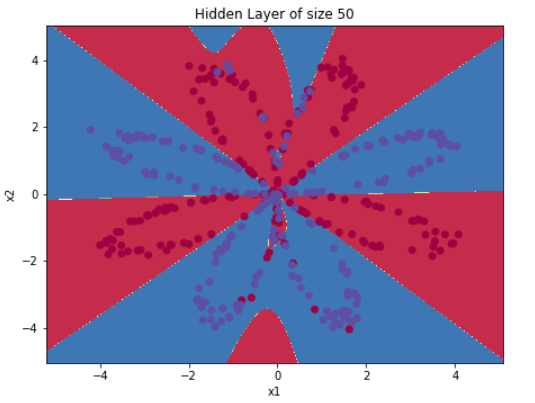

✅ 效果：

• 使用 plot_decision_boundary 绘制出模型划分的区域
• 可以看到，即使数据是非线性可分的，神经网络也能画出弯曲的边界进行分类

---

🧠 十一、关键知识点总结

概念	作用
前向传播	计算预测值
损失函数	衡量预测误差
反向传播	计算梯度
梯度下降	更新参数以最小化损失
隐藏层	提供非线性表达能力

---

💡 十二、常见问题与改进方向

1. 激活函数选择 ：建议将 tanh 改为 sigmoid 或 ReLU 更符合实际应用
2. 损失函数 ：应使用 sigmoid + binary cross entropy 保证数值稳定性
3. 正则化：可加入 L2 正则项防止过拟合
4. 优化器：可尝试 Adam、RMSProp 等现代优化算法
5. 多层网络：扩展为更深的网络（如 2 层隐藏层）

---

✅ 结语

通过这篇文章，你已经亲手实现了一个完整的浅层神经网络！虽然它简单，但它包含了深度学习的核心思想：

前向传播 → 计算损失 → 反向传播 → 参数更新

这正是所有深度学习框架背后的底层逻辑。

---

🌱 记住：真正的理解来自于亲手编码。

当你能写出这段代码，并读懂每一行的意义时，你就不再是"黑箱使用者"，而是真正的 AI 探索者。