目录
摘要
本篇文章学习尚硅谷深度学习教程,学习内容是激活函数的代码部分包括阶跃函数,sigmod函数,tanh函数,ReLu函数。
激活函数
下图中,h(x)可以将输入的信号加权总和转换为输出信号,被称为激活函数。
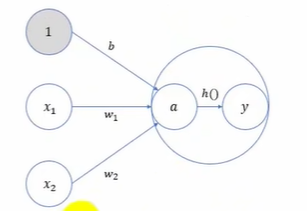
激活函数是连接感知机和神经网络的桥梁,在神经网络中起着至关重要的作用。如果没有激活函数,整个神经网络就等效于单层线性变换,不论如何加深层数,总是存在与之等效的"无隐藏层的神经网络"。激活函数必须是非线性函数,也正是激活函数的存在为神经网络引入了非线性,使得神经网络能够学习和表示复杂的非线性关系。
1.阶跃函数
下图表示的h(x)就是最简单的激活函数,它可以为输入设置一个"阈值";一旦超过这个阈值,就切换输出(0或者1)。这种函数被称为"阶跃函数"。

2.sigmod函数
函数表达式及其导函数表达式和函数图像如下
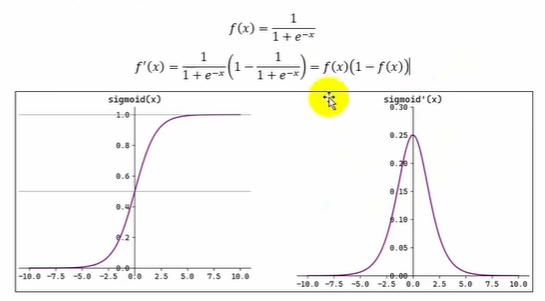
Sigmoid(也叫 Logistic 函数)是平滑的、可微的,能将任意输入映射到区间(0.1)。常用于二分类的输出层。但因其涉及指数运算,计算量相对较高。Sigmoid 的输入在[-6,6]之外时,其输出值变化很小,可能导致信息丢失。Sigmoid 的输出并非以0为中心,其输出值均>0,导致后续层的输入始终为正,可能影响后续梯度更新方向。Sigmoid 的导数范围为(0,0.25),梯度较小。当输入在[-6,6]之外时,导数接近 0,此时网络参数的更新将会极其缓慢。使用Sigmoid作为激活函数,可能出现梯度消失(在逐层反向传播时,梯度会星指数级衰减)。
3.Tanh函数
在神经网络中除了sigmod函数之外,tanh函数(双曲正切函数)也比较常用。tanh函数在sigmod函数做了一些调整,tanh函数表达式及其导函数表达式和函数图像如下
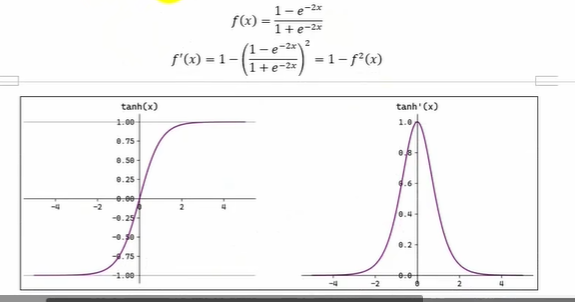
Tanh(双曲正切)将输入映射到区间(-1,1)。其关于原点中心对称。常用在隐藏层。输入在[-3,3]之外时,Tanh 的输出值变化很小,此时其导数接近 0。Tanh 的输出以0为中心,且其度相较于sigmoid 更大,收敛速度相对更快。但同样也存在梯度消失现象。
4.ReLu函数
ReLu函数表达式及其导函数表达式和函数图像如下
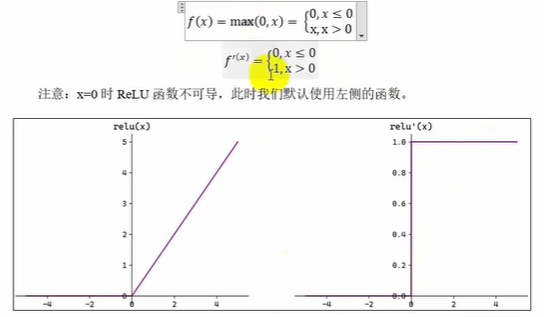
ReLU(RectifedLimearUnit,修正线性单元)会将小于0的输入转换为0,大于等于0的输入则保持不变。ReLU定义简单,计算量小。常用于隐藏层。
ReLU 作为激活函数不存在梯度消失。当输入小于0时,ReLU的输出为0,这意味着在神经网络中,ReLU激活的节点只有部分是"活跃"的,这种稀疏性有助于减少计算量和提高模型的效率。
当神经元的输入持续为负数时,ReLU的输出始终为0。这意味着神经元可能永远不会被激活,从而导致"神经元死亡"问题。这会影响模型的学习能力,特别是如果大量的神经元都变成了"死神经元"。为解决此问题,可使用LeakyReLU 来代替 ReLU 作为激活函数。
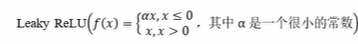
在负数区域引入一个小的斜率来解决"神经元死亡"问题。
代码实践
学到的函数都比较常用,因此创建python工具包方便以后调用
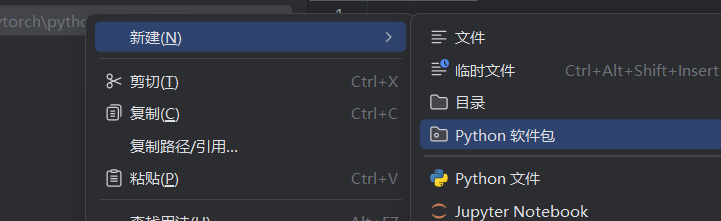
1.阶跃函数
接下来实现阶跃函数,按上面的思路可以写出一个简单的阶跃函数,只需要判断即可
python
#阶跃函数
def step_function0(x):
if x>0
return 1
else:
return 0但实际中并不一定输入一个标量,往往是输入一个向量。因此引用numpy库中的array函数。
python
import numpy as np
def step_function(x):
return np.array(x > 0,dtype= int)测试
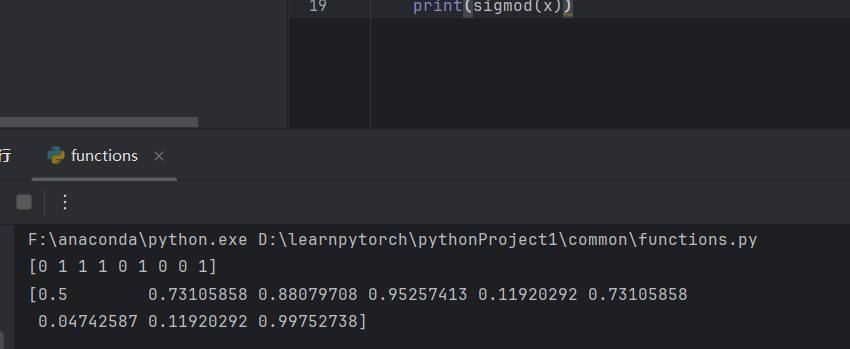
2.sigmod函数
python
#sigmod函数
def sigmod(x):
return 1/(1+np.exp(-x))测试
3.tanh函数
在numpy中已经有tanh函数,直接调用即可

4.ReLu函数
python
#ReLu函数
def relu(x):
return np.maximum(0,x)测试
