动态规划、贪心算法和分治算法作为三大经典算法范式,各自具有独特的思想体系和适用场景。本文将深入探讨这三种算法的理论基础、设计思想、应用场景以及它们之间的内在联系与区别。
一、动态规划(Dynamic Programming)
1.1 基本概念与核心思想
动态规划是一种解决多阶段决策过程最优化问题的方法论。其核心思想是将复杂问题分解为相互重叠的子问题,通过保存子问题的解避免重复计算,最终构建原问题的最优解。
形式化定义 :
对于问题P,若其满足最优子结构性质,即问题的最优解包含其子问题的最优解,且子问题之间存在重叠,则可采用动态规划求解。
1.2 动态规划的理论基础
贝尔曼方程(Bellman Equation)
动态规划的理论基础是贝尔曼最优性原理,其数学表达为:
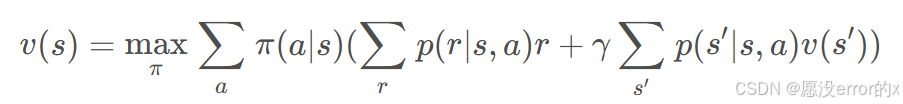
其中:
-
V(s)表示状态s的最优值函数
-
R(s,a)表示在状态s采取动作a的即时奖励
-
P(s′|s,a)表示状态转移概率
-
γ为折扣因子
动态规划的两个关键性质
-
最优子结构:问题的最优解包含子问题的最优解
-
重叠子问题:递归算法会反复求解相同的子问题
1.3 动态规划的两种实现方式
自顶向下带备忘录的递归方法
python
def fibonacci_memo(n, memo={}):
if n in memo:
return memo[n]
if n <= 2:
return 1
memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)
return memo[n]自底向上的迭代方法
python
def fibonacci_dp(n):
if n <= 2:
return 1
dp = [0] * (n+1)
dp[1] = dp[2] = 1
for i in range(3, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]1.4 经典问题解析:0-1背包问题
问题描述:给定n个物品,每个物品有重量wᵢ和价值vᵢ,背包容量为W,求如何选择物品使得总价值最大且总重量不超过W。
状态定义 :
设dp[i][j]表示考虑前i个物品,背包容量为j时的最大价值。
状态转移方程:
cpp
dp[i][j] = max(dp[i-1][j], dp[i-1][j-wᵢ] + vᵢ) if j ≥ wᵢ
dp[i-1][j] otherwise空间优化版本:
python
def knapsack_01(weights, values, capacity):
n = len(weights)
dp = [0] * (capacity + 1)
for i in range(n):
for j in range(capacity, weights[i]-1, -1):
dp[j] = max(dp[j], dp[j-weights[i]] + values[i])
return dp[capacity]1.5 动态规划的进阶应用
序列对齐问题(Sequence Alignment)
在生物信息学中,DNA序列对齐是动态规划的重要应用:
python
def sequence_alignment(X, Y, gap_penalty, mismatch_penalty):
m, n = len(X), len(Y)
dp = [[0] * (n+1) for _ in range(m+1)]
# 初始化边界条件
for i in range(m+1):
dp[i][0] = i * gap_penalty
for j in range(n+1):
dp[0][j] = j * gap_penalty
# 填充dp表
for i in range(1, m+1):
for j in range(1, n+1):
if X[i-1] == Y[j-1]:
match = dp[i-1][j-1]
else:
match = dp[i-1][j-1] + mismatch_penalty
delete = dp[i-1][j] + gap_penalty
insert = dp[i][j-1] + gap_penalty
dp[i][j] = min(match, delete, insert)
return dp[m][n]二、贪心算法(Greedy Algorithm)
2.1 基本概念与核心思想
贪心算法在每一步选择中都采取当前状态下最优的选择,期望通过局部最优解的累积达到全局最优解。
贪心选择性质:问题的全局最优解可以通过一系列局部最优选择达到。
2.2 贪心算法的理论基础
拟阵理论(Matroid Theory)
贪心算法的正确性可以通过拟阵理论得到严格证明。一个系统(M, I)是拟阵当且仅当满足:
-
遗传性:如果B ∈ I且A ⊆ B,则A ∈ I
-
交换性:如果A, B ∈ I且|A| < |B|,则存在x ∈ B-A使得A∪{x} ∈ I
定理:在加权拟阵上,贪心算法总能找到最优解。
2.3 贪心算法的证明技术
交换论证(Exchange Argument)
证明贪心算法正确性的关键技术:
-
假设存在一个最优解O和贪心解G
-
通过逐步将O转换为G,证明每一步转换不会降低解的质量
-
最终证明G至少与O一样好
2.4 经典问题解析:霍夫曼编码
问题描述:给定字符集和频率,构造前缀编码使得编码长度最小。
贪心策略:每次选择频率最小的两个节点合并
python
import heapq
class Node:
def __init__(self, char, freq, left=None, right=None):
self.char = char
self.freq = freq
self.left = left
self.right = right
def __lt__(self, other):
return self.freq < other.freq
def build_huffman_tree(chars, freqs):
nodes = [Node(char, freq) for char, freq in zip(chars, freqs)]
heapq.heapify(nodes)
while len(nodes) > 1:
left = heapq.heappop(nodes)
right = heapq.heappop(nodes)
parent = Node(None, left.freq + right.freq, left, right)
heapq.heappush(nodes, parent)
return nodes[0]
def generate_codes(root, code="", codes={}):
if root is None:
return
if root.char is not None:
codes[root.char] = code
generate_codes(root.left, code + "0", codes)
generate_codes(root.right, code + "1", codes)
return codes2.5 贪心算法的局限性
贪心算法并不总是能得到全局最优解,如:
-
0-1背包问题(贪心解法不是最优)
-
图着色问题
-
旅行商问题
三、分治算法(Divide and Conquer)
3.1 基本概念与核心思想
分治算法将问题分解为若干个规模较小但结构与原问题相似的子问题,递归解决这些子问题,然后合并子问题的解得到原问题的解。
分治三步骤:
-
分解(Divide):将原问题分解为子问题
-
解决(Conquer):递归求解子问题
-
合并(Combine):将子问题的解合并为原问题的解
3.2 分治算法的复杂度分析
主定理(Master Theorem)
对于递归式T(n) = aT(n/b) + f(n),其中a ≥ 1, b > 1:
-
若f(n) = O(n^(log_b a - ε)),ε > 0,则T(n) = Θ(n^(log_b a))
-
若f(n) = Θ(n^(log_b a) log^k n),k ≥ 0,则T(n) = Θ(n^(log_b a) log^(k+1) n)
-
若f(n) = Ω(n^(log_b a + ε)),ε > 0,且af(n/b) ≤ cf(n),c < 1,则T(n) = Θ(f(n))
3.3 经典问题解析:快速排序
python
def quicksort(arr, low, high):
if low < high:
# 分区操作
pi = partition(arr, low, high)
# 递归排序
quicksort(arr, low, pi-1)
quicksort(arr, pi+1, high)
def partition(arr, low, high):
pivot = arr[high]
i = low - 1
for j in range(low, high):
if arr[j] <= pivot:
i += 1
arr[i], arr[j] = arr[j], arr[i]
arr[i+1], arr[high] = arr[high], arr[i+1]
return i+13.4 分治算法的进阶应用:Strassen矩阵乘法
传统矩阵乘法时间复杂度为O(n³),Strassen算法通过分治将其降低到O(n^2.81):
python
def strassen_multiply(A, B):
n = len(A)
# 基础情况
if n == 1:
return [[A[0][0] * B[0][0]]]
# 分割矩阵
mid = n // 2
A11 = [row[:mid] for row in A[:mid]]
A12 = [row[mid:] for row in A[:mid]]
A21 = [row[:mid] for row in A[mid:]]
A22 = [row[mid:] for row in A[mid:]]
B11 = [row[:mid] for row in B[:mid]]
B12 = [row[mid:] for row in B[:mid]]
B21 = [row[:mid] for row in B[mid:]]
B22 = [row[mid:] for row in B[mid:]]
# 计算7个乘积矩阵
M1 = strassen_multiply(matrix_add(A11, A22), matrix_add(B11, B22))
M2 = strassen_multiply(matrix_add(A21, A22), B11)
M3 = strassen_multiply(A11, matrix_sub(B12, B22))
M4 = strassen_multiply(A22, matrix_sub(B21, B11))
M5 = strassen_multiply(matrix_add(A11, A12), B22)
M6 = strassen_multiply(matrix_sub(A21, A11), matrix_add(B11, B12))
M7 = strassen_multiply(matrix_sub(A12, A22), matrix_add(B21, B22))
# 计算结果矩阵的四个部分
C11 = matrix_add(matrix_sub(matrix_add(M1, M4), M5), M7)
C12 = matrix_add(M3, M5)
C21 = matrix_add(M2, M4)
C22 = matrix_add(matrix_sub(matrix_add(M1, M3), M2), M6)
# 合并结果
C = []
for i in range(mid):
C.append(C11[i] + C12[i])
for i in range(mid):
C.append(C21[i] + C22[i])
return C四、三种算法的比较与分析
4.1 算法特性对比
| 特性 | 动态规划 | 贪心算法 | 分治算法 |
|---|---|---|---|
| 子问题关系 | 重叠子问题 | 独立选择 | 独立子问题 |
| 求解顺序 | 自底向上/自顶向下 | 一步到位 | 递归分解 |
| 最优性 | 保证全局最优 | 可能非最优 | 保证正确解 |
| 时间复杂度 | 通常多项式时间 | 通常较低 | 依赖递归式 |
| 空间复杂度 | 通常较高 | 通常较低 | 依赖递归深度 |
4.2 适用场景分析
动态规划适用场景:
-
问题具有最优子结构
-
子问题有重叠
-
需要记录历史决策
-
如:最短路径、序列对齐、资源分配
贪心算法适用场景:
-
问题具有贪心选择性质
-
局部最优能导致全局最优
-
如:最小生成树、霍夫曼编码、区间调度
分治算法适用场景:
-
问题可自然分解为独立子问题
-
子问题解可高效合并
-
如:排序、矩阵乘法、快速傅里叶变换
4.3 算法选择策略
-
分析问题结构:检查是否具有最优子结构、重叠子问题等特性
-
验证算法性质:确认是否满足贪心选择性质或可分治性质
-
考虑复杂度要求:评估时间、空间复杂度的可接受范围
-
实现复杂度:权衡算法实现难度与性能收益