在阅读本文之前,建议读者优先阅读本专栏内前面的文章。
目录
前言
本文主要通过力扣和牛客网站上的几篇文章来介绍与单链表相关的几种经典算法。
一、单链表相关经典算法OJ题1:移除链表元素
我在这里给出题目测试链接:
题目详细叙述如下:
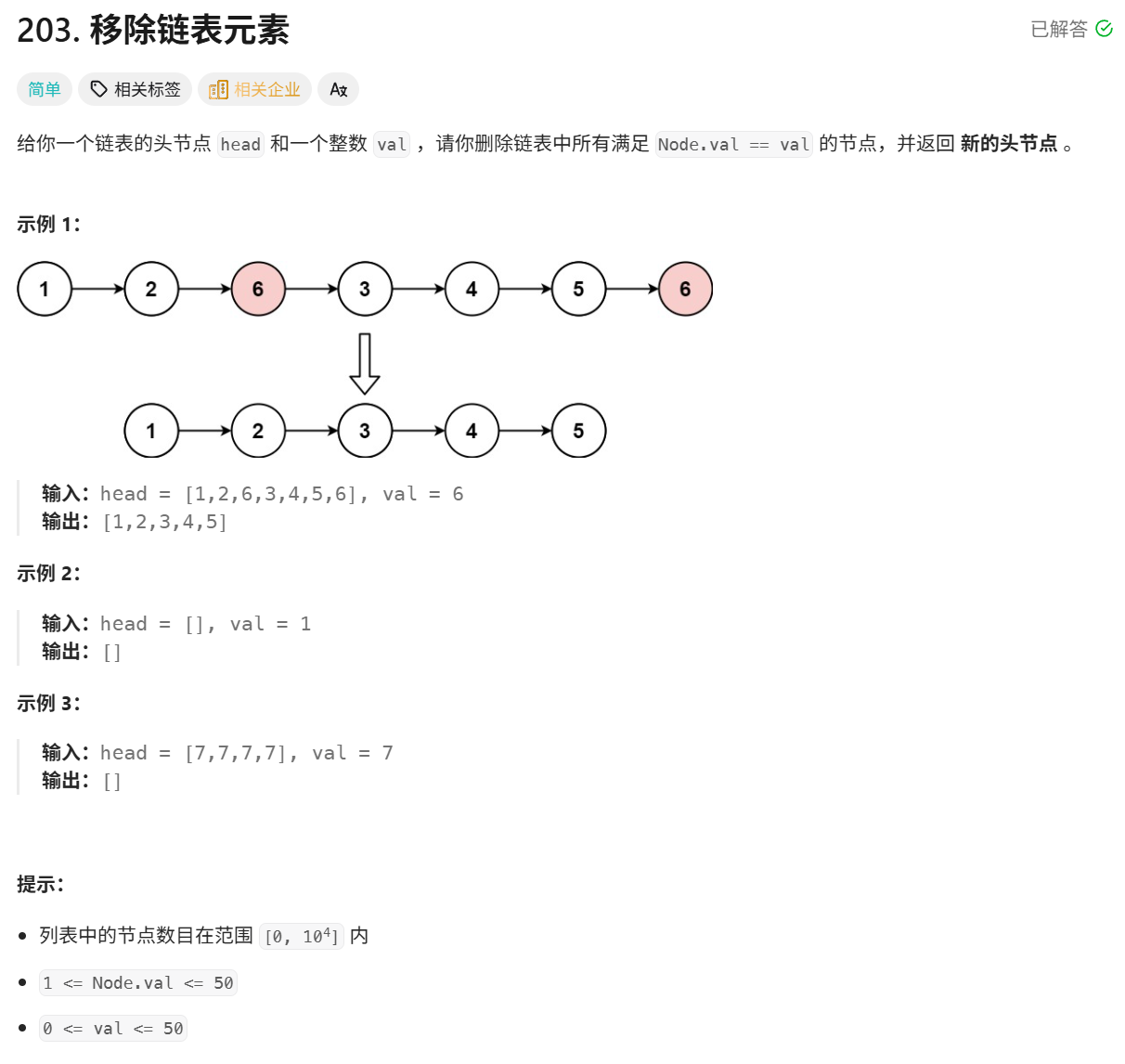
这道题的思路应该是什么呢?
思路一:
我的思路是将整体逻辑分为两部分:处理头部节点和处理中间及尾部节点,具体为首先进行空链表判断,若链表为空,直接返回head,无需处理。当链表头部存在值为val的节点时,需要将头指针head后移,直到头部节点的值不等于val。用prev指针初始指向head,通过循环判断prev是否为目标节点。若为目标节点,prev后移,同时更新head为新的头部。处理中间及尾部的目标节点时,当头部处理完毕后(prev指向非目标节点),用pcur指针遍历后续节点,通过prev记录pcur的前驱节点,实现中间节点的删除。若pcur是目标节点,则让prev->next跳过pcur,释放pcur的内存,再将pcur更新为prev->next(继续遍历)。若pcur不是目标节点,则prev和pcur同时后移(保持前驱关系)。
那么我给出我的示例代码:
cpp
typedef struct ListNode node;
struct ListNode* removeElements(struct ListNode* head, int val) {
if (head == NULL) {
return head;
}
node* prev = head;
while (prev != NULL && prev->val == val) {
prev = prev->next;
free(head);
head = prev;
}
if (prev != NULL) {
node* pcur = prev->next;
while (pcur != NULL) {
if (pcur->val == val) {
prev->next = pcur->next;
free(pcur);
pcur = prev->next;
} else {
pcur = pcur->next;
prev = prev->next;
}
}
}
return head;
}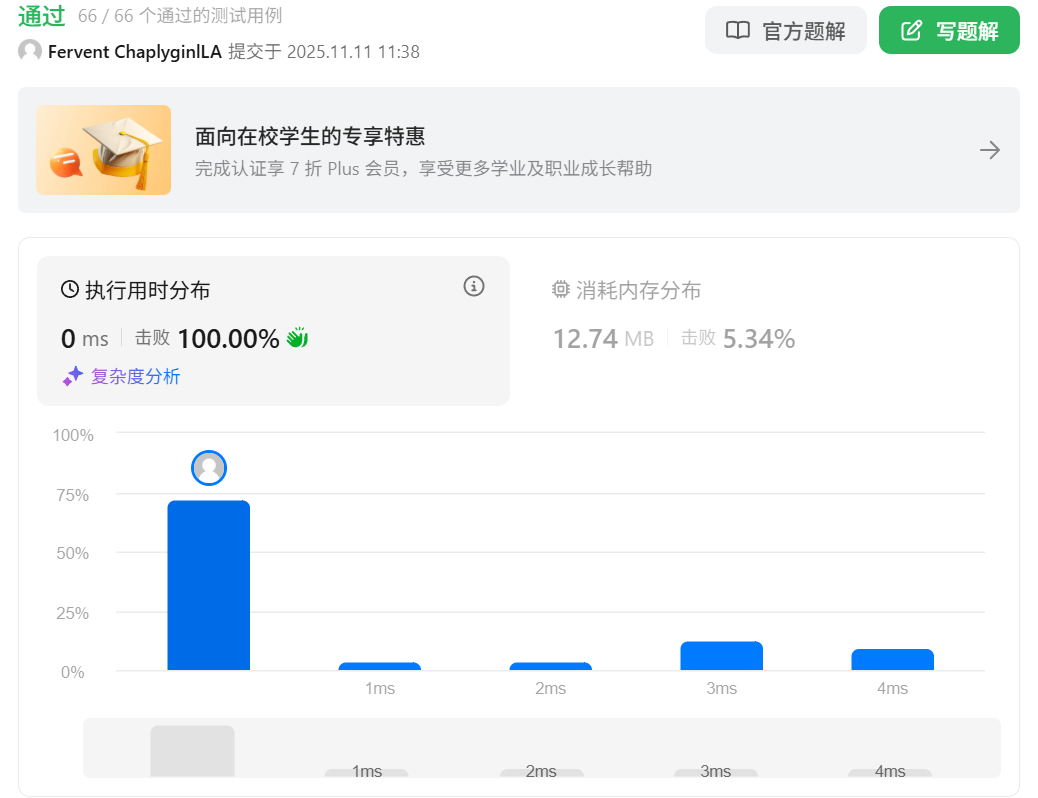
从结果来看,我们的代码应该不是很高效,那么大概问题出现在哪里呢?我询问了AI,它是这么说明的:处理头部节点时,prev的初始值为head,循环中head随prev同步更新,逻辑稍显冗余。可通过引入 "虚拟头节点" 简化头部和中间节点的处理逻辑(统一删除逻辑)。
思路二:
那么其实我们也可以采取下面这种思路,就是申请一个新的链表,然后将原链表遍历,当节点的存储值是我们输入的值的时候,我们就跳过它,否则我们就尾插入新链表。那么这种思路我们该如何去实现呢?我给出示例的代码:
cpp
typedef struct ListNode node;
struct ListNode* removeElements(struct ListNode* head, int val) {
//创建一个空链表
node* newHead = NULL;
node* newTail = NULL;
//遍历原链表
node* pcur = head;
while(pcur){
//尾插
if(pcur->val != val){
//链表为空
if(newHead == NULL){
newHead = newTail = pcur;
}else{
//链表不为空
newTail->next = pcur;
newTail = newTail->next;
}
}
pcur = pcur->next;
}
if(newTail) newTail->next = NULL;
return newHead;
}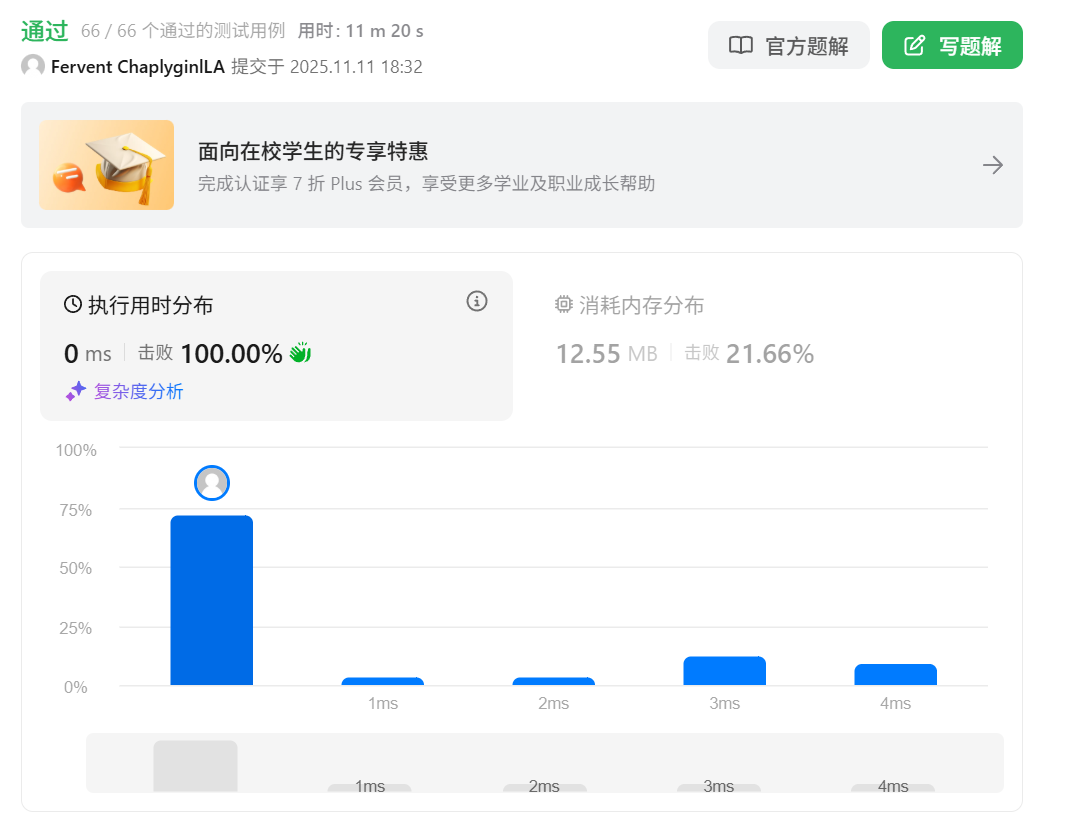
可以看到,我们的确提高了一点点的效率,但是并没有提高太多。我们这里来看一下排名较高的解法具体什么样子:
思路三:
这种解法为我们介绍了链表的递归解法,这是因为链表具有天然的递归性,我们以下面图片举例:

我们可以将原链表看成头节点 1 后挂接一个更短的链表:
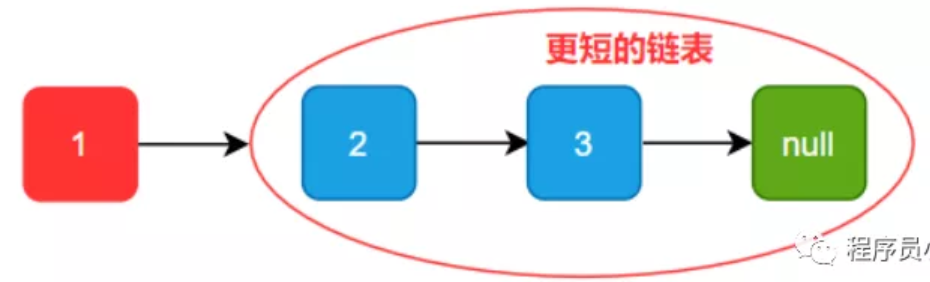
继续拆解到无法继续拆的程度:
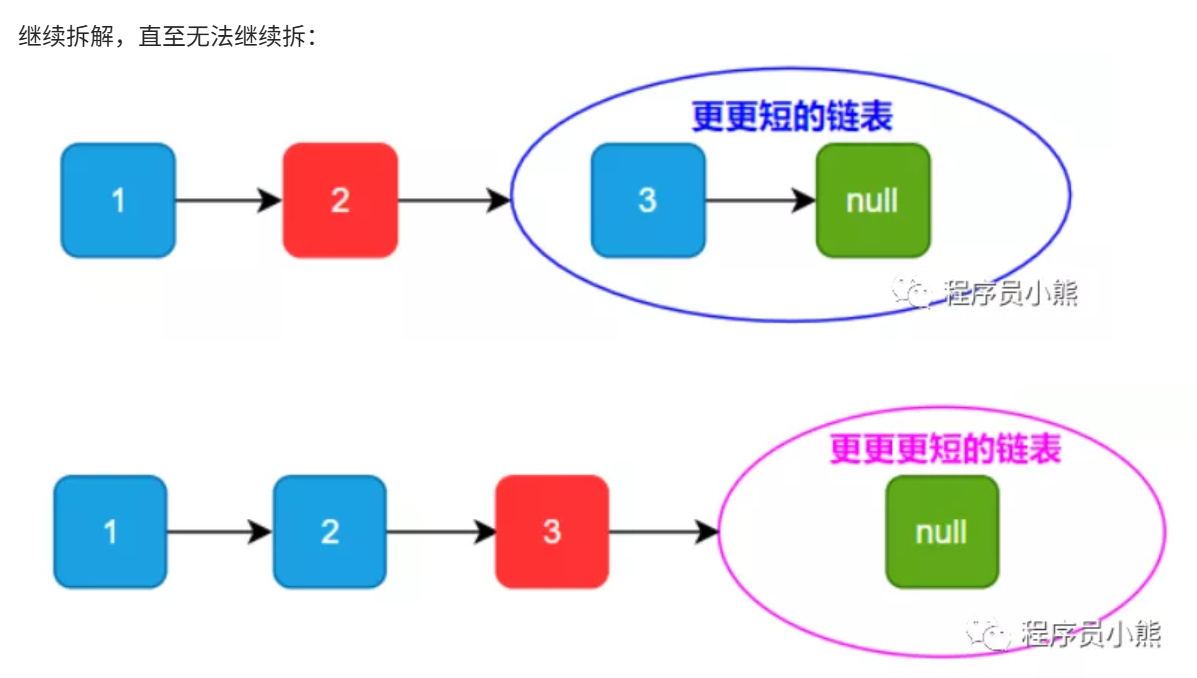
有了这样的思考,链表中的很多操作,都可以采用递归这种逻辑思维方式去完成。
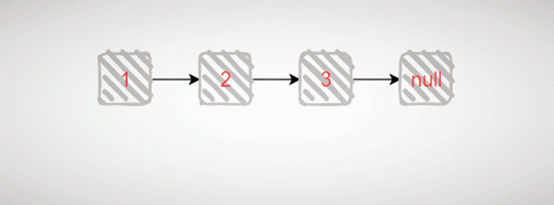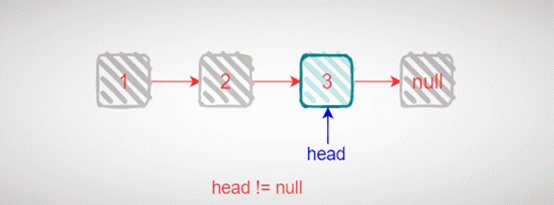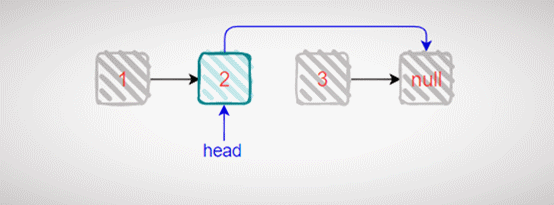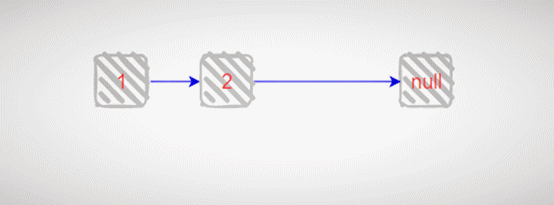
例如本题,如下图示:
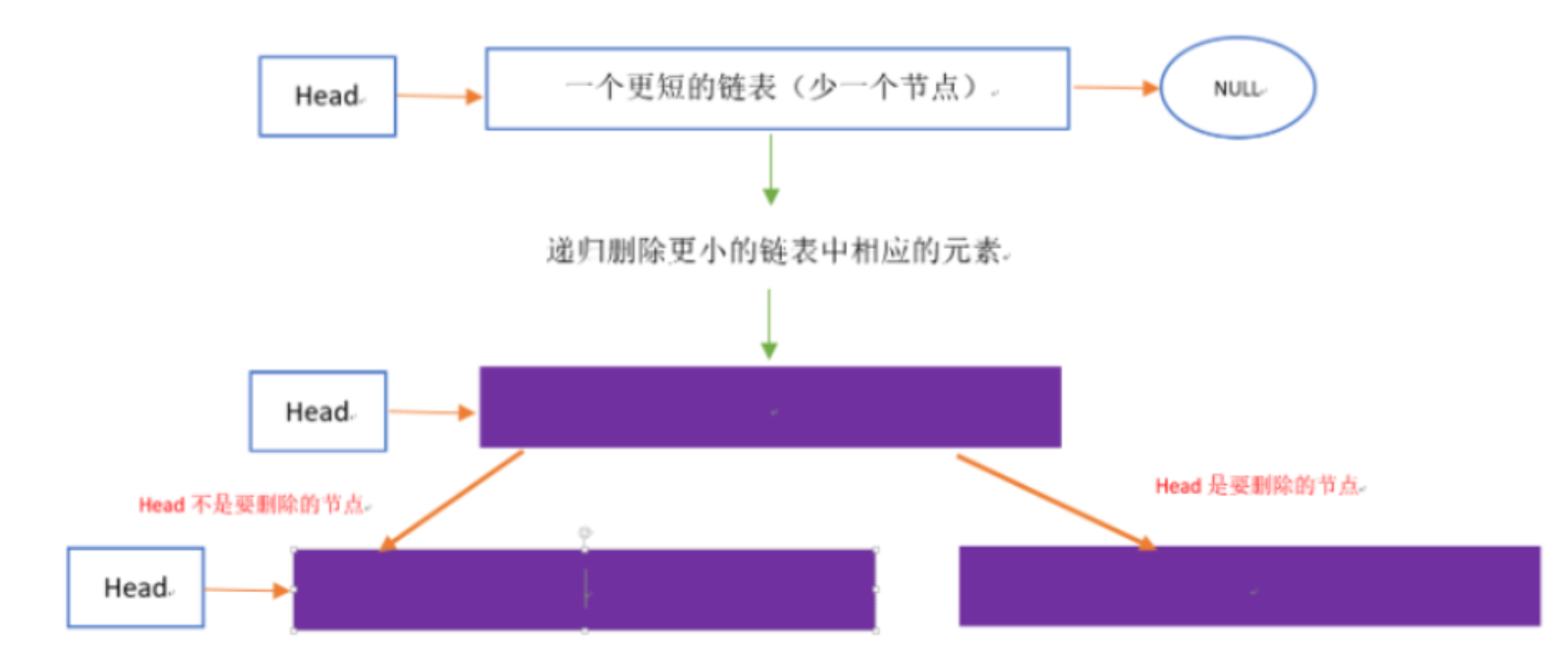
如果头节点的值不等于val,原问题的结果为头节点后挂接子问题求得的紫色的链表,否则,结果就为子问题求得的紫色的链表。以链表 1->2->3-null 为例子,删除值为 3 的节点,递归的具体过程如下动图示:
其运行代码如下:
cpp
struct ListNode* removeElements(struct ListNode* head, int val){
if (NULL == head) {
return head;
}
head->next = removeElements(head->next, val);
return head->val == val ? head->next : head;
}
很明显,这种递归的方法,一定会开出很多的栈帧,所以它消耗内存也是比较多。
思路四:
既然我们可以用递归的方式解决,那么我们也一定可以用迭代的方式解决,这种解决方式和我们第一种解决方法比较相似,只不过它创建了一个哨兵节点,也就是一个不存放值的节点,它直接指向我们传入的头结点:
cpp
struct ListNode* removeElements(struct ListNode* head, int val) {
struct ListNode* dummyHead = (struct ListNode*)malloc(sizeof(struct ListNode));
dummyHead->next = head; // 指向真正的头节点
dummyHead->val = 0; // 值不重要,可以是任意值
struct ListNode* temp = head;
struct ListNode* prev = dummyHead;
while(temp){
if(temp&&temp->val==val){
while(temp&&temp->val==val){
temp=temp->next;
}
prev->next=temp;
}
else{
prev=temp;
temp=temp->next;
}
}
head = dummyHead->next;
free(dummyHead);
return head;
}
那么这道题到这就彻底结束了。
二、单链表相关经典算法OJ题2:反转链表
我这里给出题目测试链接:
题目详细叙述如下:
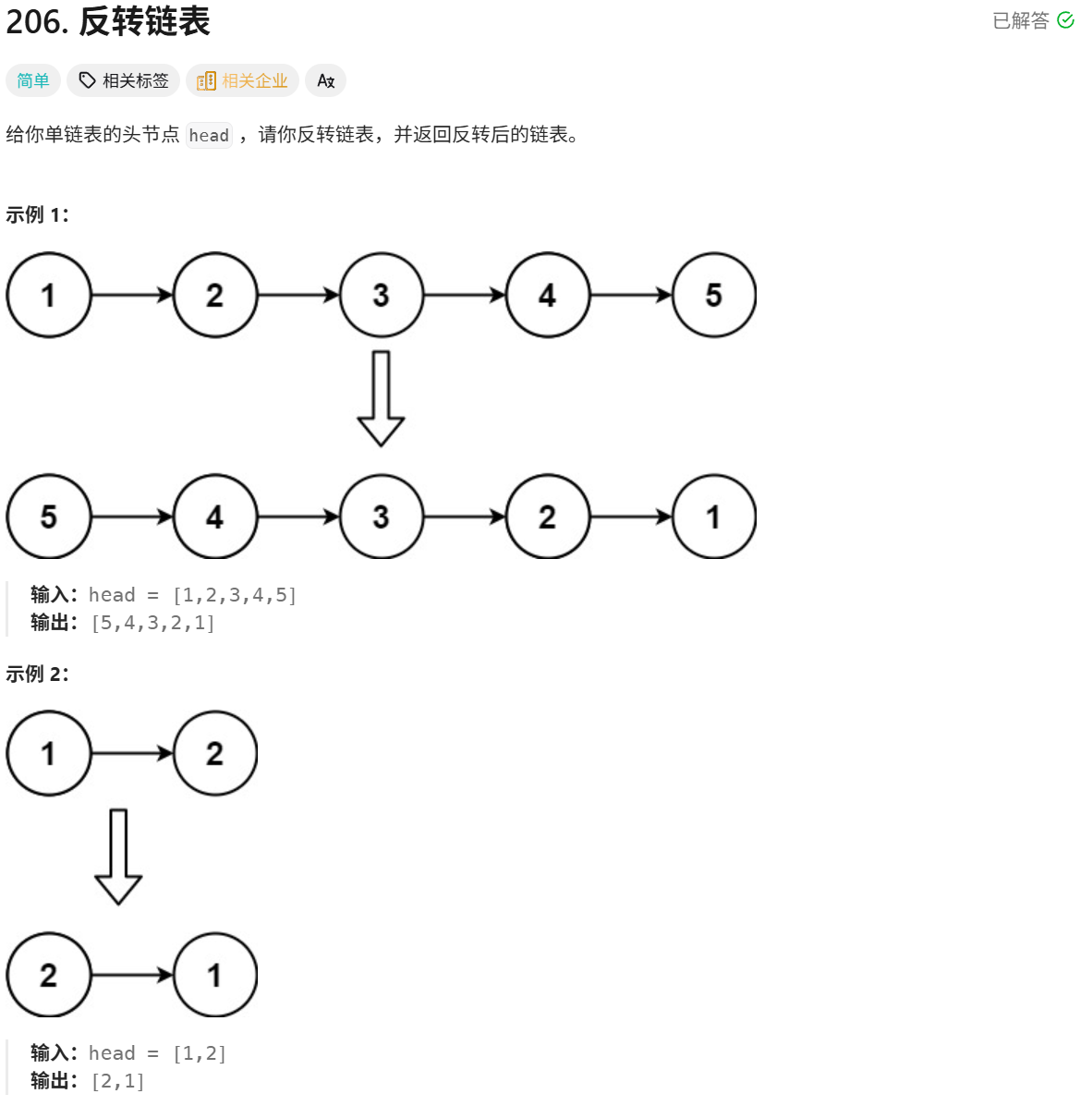
那么我们该如何解决这道题呢?
思路一:
其实我们完全可以创建一个新链表,然后遍历原链表中的节点头插到新链表,请读者思考代码该如何实现,我给出示例代码:
cpp
typedef struct ListNode node;
struct ListNode* reverseList(struct ListNode* head) {
node* newHead = NULL;
node* newTail = NULL;
if(head == NULL){
return head;
}
node* pcur = head;
while(head){
if(newHead == NULL){
pcur = pcur->next;
newHead = head;
newTail = newHead;
head = pcur;
}else{
pcur = pcur->next;
head->next = newHead;
newHead = head;
head = pcur;
}
}
newTail->next = NULL;
return newHead;
}
思路二:
我们接下来介绍一种相对简单的解法。我们可以创建三个指针,然后用这三个指针完成反转操作,该方法本质上是使用了迭代的思想。空链表判断若链表为空,直接返回head,无需处理。初始化三个指针,首先n1初始化为NULL,用于指向当前节点的前一个节点;然后n2初始化为head,指向当前需要处理的节点;最后n3初始化为n2->next,用于暂存当前节点的后一个节点。然后我们迭代反转节点指针循环处理每个节点。第一步将n2的next指针反转,指向n1;第二步将n1后移,更新为当前的n2;第三步将n2后移,更新为之前暂存的n3;第四步若n3不为NULL,则n3后移,为下一次循环做准备。返回新的头节点循环结束后,n2为NULL,n1指向原链表的最后一个节点,因此返回n1。请读者思考代码实现:
cpp
typedef struct ListNode node;
struct ListNode* reverseList(struct ListNode* head) {
if(head == NULL) return head;
node* n1 = NULL;
node* n2 = head;
node* n3 = n2->next;
while(n2){
n2->next = n1;
n1 = n2;
n2 = n3;
if(n3) n3= n3->next;
}
return n1;
}
思路三:
同样我们也可以使用递归的方式来解决这个问题,我们先递到链表的末尾节点,作为新链表的头节点。然后在归的过程中,一个一个地把节点插在新链表的末尾。新链表的末尾节点在哪?就是当前节点的 next。具体实现如下:
cpp
struct ListNode* reverseList(struct ListNode* head) {
if (head == NULL || head->next == NULL) {
return head;
}
struct ListNode* rev_head = reverseList(head->next);
struct ListNode* tail = head->next;
tail->next = head;
head->next = NULL;
return rev_head;
}
那么本题到这就结束了。
三、单链表相关经典算法OJ题3:链表中心节点
我这里给出题目测试链接:
题目详细叙述如下:
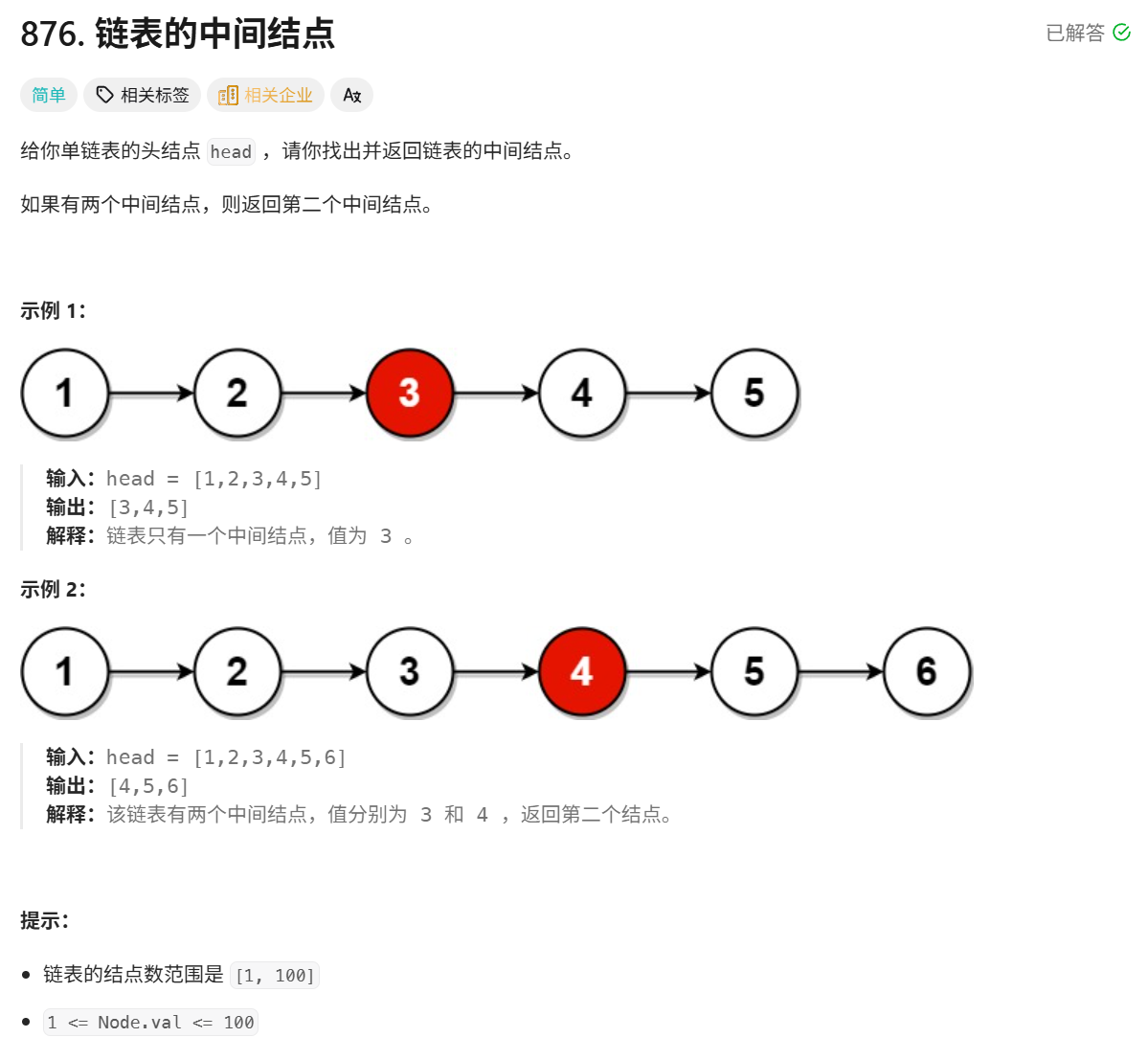
思路一:
我们其实很容易想出来这个比较暴力的解法,那就是我先求出整个链表的长度,然后根据其奇偶性来分类讨论。这种方法相对来说是比较容易写出代码的:
cpp
typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head) {
ListNode* pcur = head;
int num = 0;
while (pcur) {
num++;
pcur = pcur->next;
}
pcur = head;
if (num % 2) {
num /= 2;
for (int i = 0; i < num; i++) {
pcur = pcur->next;
}
} else {
num /= 2;
for (int i = 0; i < num; i++) {
pcur = pcur->next;
}
}
return pcur;
}
思路二:
上面的方法想得很容易,但是它是十分低效的,我们这里介绍一种方法叫做快慢指针法,在之后的解题过程中,我们在遇到比如说链表带环问题时,也可以使用这种方法。我们可以定义两个指针fast(快指针)和slow(慢指针),均初始化为指向链表的头节点head。快慢指针遍历链表循环条件为fast && fast->next,慢指针slow每次向后移动1步;快指针fast每次向后移动2步。返回中间节点,当循环结束时,慢指针slow恰好指向链表的中间节点,返回slow即可。由于快指针的移动速度是慢指针的2倍,当快指针遍历完链表时,慢指针刚好走到链表的中间位置。这时可以分两种情况,若链表长度为奇数,快指针最终会指向最后一个节点,此时慢指针指向正中间节点;若链表长度为偶数,快指针最终会指向NULL,此时慢指针指向中间两个节点中的后一个。我们给出市里的代码:
cpp
typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head) {
ListNode* fast = head;
ListNode* slow = head;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
四、单链表相关经典算法OJ题4:合并两个有序链表
我这里给出题目测试链接:
题目详细叙述如下:
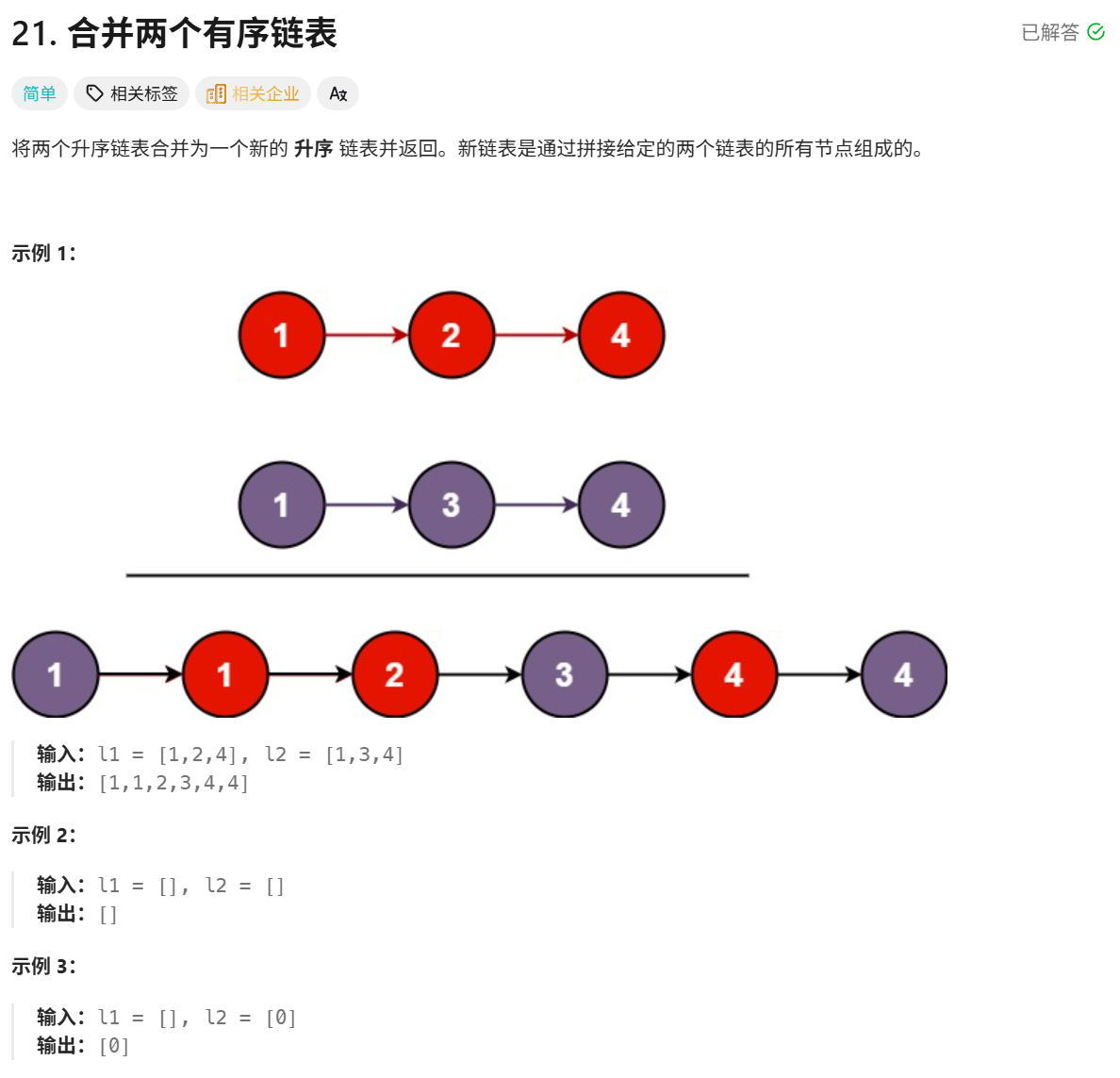
思路一:
我们这道题可以有个很容易想的思路,那就是我们直接创建一个新链表,然后遍历前面两个链表,把节点按顺序填充进去。请读者思考一下代码实现,我给出示例:
cpp
typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
ListNode* newHead;
ListNode* newTail;
newHead = newTail = NULL;
ListNode* n1 = list1;
ListNode* n2 = list2;
if(n1 == NULL){
if(n2 == NULL){
return NULL;
}else{
return n2;
}
}
if(n2 == NULL){
if(n1 == NULL){
return NULL;
}else{
return n1;
}
}
if(newHead == NULL){
if(n1->val < n2->val){
newHead = n1;
n1 = n1->next;
}else{
newHead = n2;
n2 = n2->next;
}
}
newTail = newHead;
while((n1 != NULL) && (n2 != NULL)){
if(n1->val < n2->val){
newTail->next = n1;
n1 = n1->next;
}else{
newTail->next = n2;
n2 = n2->next;
}
newTail = newTail->next;
}
if(n1 == NULL){
newTail->next = n2;
}
if(n2 == NULL){
newTail->next = n1;
}
return newHead;
}
思路二:
上面这段代码实在是太长了,我们想一想是否可以用递归的方法来实现这段代码呢?首先先讨论空链表情况,若链表l1为空,说明剩余节点只能来自l2,直接返回l2;若链表l2为空,说明剩余节点只能来自l1,直接返回l1。递归的核心逻辑则是针对非空的l1和l2,比较两个链表当前头节点的值,
若l1->val<l2->val,说明l1的当前节点是合并后链表的下一个节点。此时只需递归处理l1的剩余部分和l2,并将递归结果挂到l1->next上,最后返回l1;否则说明l2的当前节点是合并后链表的下一个节点。此时递归处理l1和l2的剩余部分,并将递归结果挂到l2->next上,最后返回l2。也就是如下的代码:
cpp
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2) {
if (l1 == NULL) {
return l2;
}
else if (l2 == NULL) {
return l1;
}
else if (l1->val < l2->val) {
l1->next = mergeTwoLists(l1->next, l2);
return l1;
}
else {
l2->next = mergeTwoLists(l1, l2->next);
return l2;
}
}
那么这道题就到此结束了。
五、环形链表的约瑟夫问题
据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus和他的朋友并不想遵从,Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
我这里给出题目的测试链接:
题目详细叙述如下:
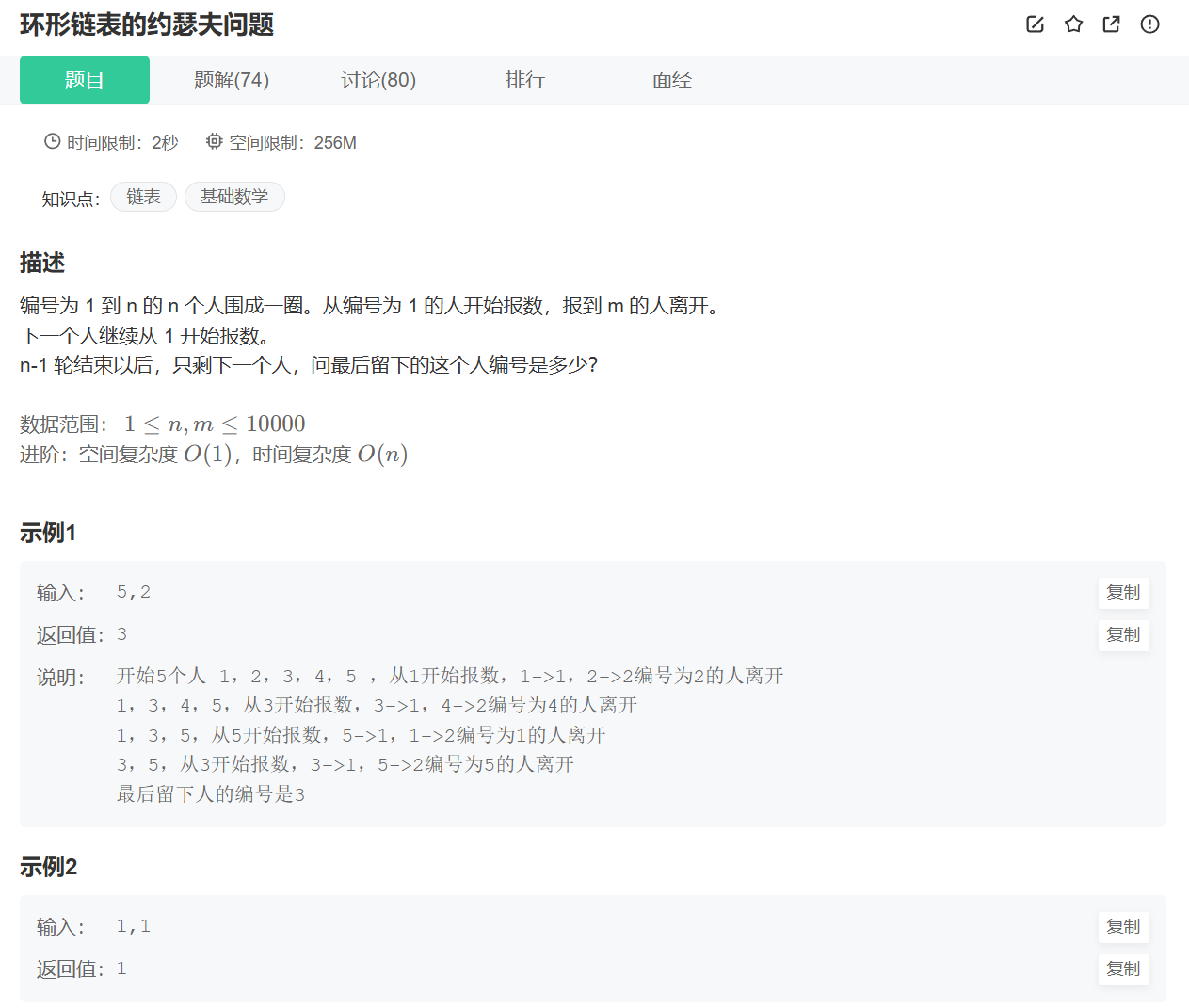
那么这道题的思路是什么呢?我们首先生成包含n个节点的循环链表,每个节点的值代表人的初始位置。用buynode函数创建单个节点,先创建第一个节点(值为1),作为初始头节点phead,同时用ptail指向尾节点。然后循环创建后续节点,每次将新节点挂到ptail的next,并更新ptail为新节点。最后将尾节点ptail的next指向头节点phead,形成循环结构,返回值为ptail。然后我们初始化如下指针,prev指向循环链表的尾节点;pcur指向当前报数的节点;count作为报数计数器。然后我们循环淘汰节点,循环条件为pcur != prev,若count == m,淘汰pcur节点,让prev->next指向pcur->next,释放pcur的内存,再将pcur更新为prev->next,然后重置count为1;若count != m,就让prev和pcur同时后移,count加1。最后当循环结束时,pcur和prev指向同一个节点,返回该节点的值。根据上面的思路请读者思考如何实现代码,我下面给出示例:
cpp
typedef struct ListNode node;
node* buynode(int x){
node* lnode = (node*)malloc(sizeof(node));
lnode->val = x;
lnode->next = NULL;
return lnode;
}
node* createcircle(int n){
node* phead = buynode(1);
node* ptail = phead;
for(int i = 2; i <= n; i++){
node* pnode = buynode(i);
ptail->next = pnode;
ptail = ptail->next;
}
ptail->next = phead;
return ptail;
}
int ysf(int n, int m ) {
node* prev = createcircle(n);
node* pcur = prev->next;
int count = 1;
while(pcur != prev){
if(count == m){
prev->next = pcur->next;
free(pcur);
pcur = prev->next;
count = 1;
}else{
prev = pcur;
pcur = pcur->next;
count++;
}
}
return pcur->val;
}
六、单链表相关经典算法OJ题5:分割链表
我这里给出题目测试链接:
面试题 02.04. 分割链表 - 力扣(LeetCode)
题目具体叙述如下:
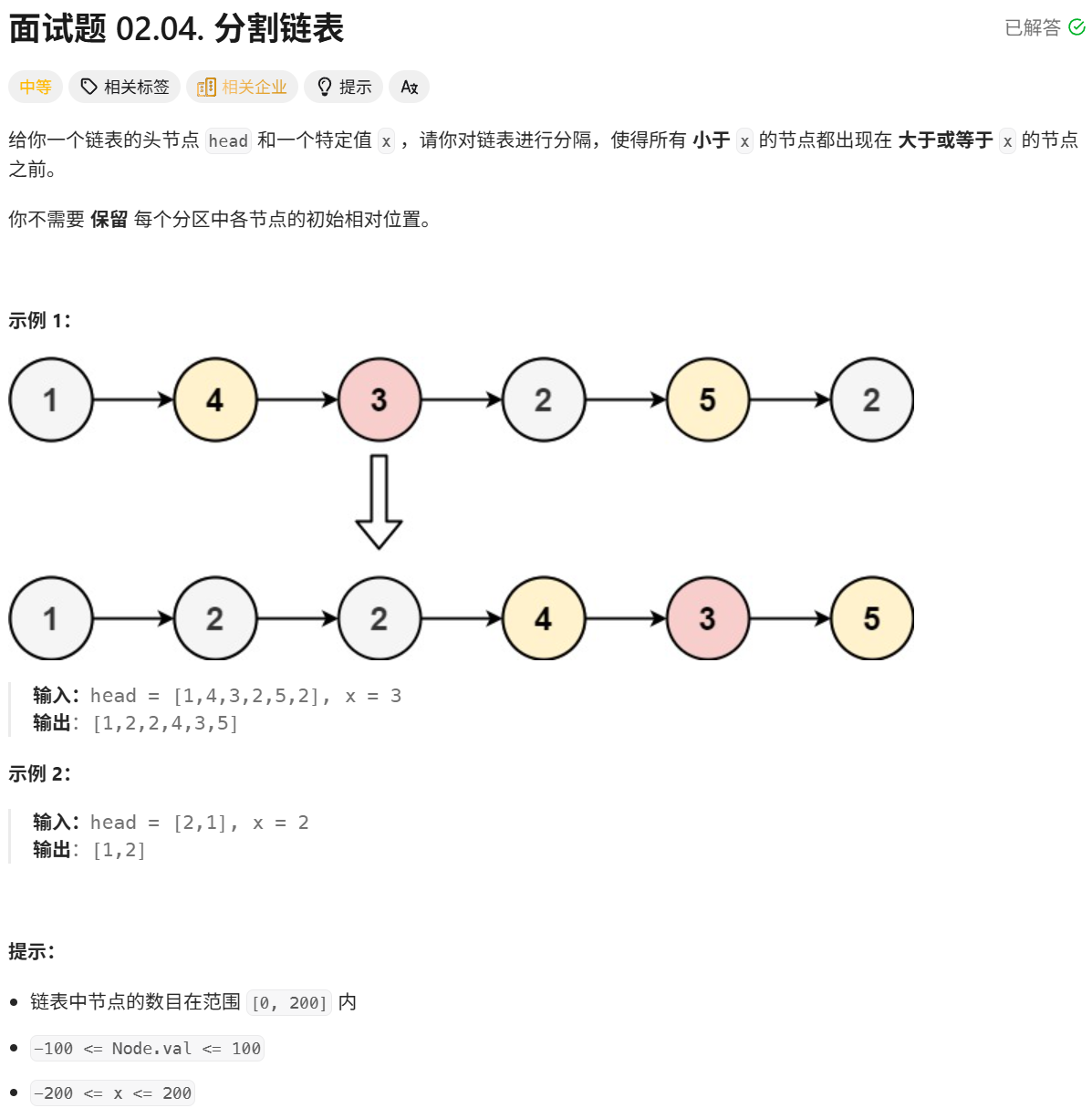
针对这道题我们应该如何去思考呢?
思路一:
一个非常简单的思路就是我直接创建两个链表,然后遍历原链表,将链表中这两部分节点分隔出来,分别存储到两部分链表之中,然后将两个链表进行合并。最后返回一个头节点指针就可以了。那么这个代码该如何实现呢?请读者进行思考,我给出我的代码:
cpp
typedef struct ListNode ListNode;
struct ListNode* partition(struct ListNode* head, int x) {
//定义两个新链表
ListNode* n1;
ListNode* n2;
ListNode* n3;
ListNode* n4;
n1 = n2 = NULL;
n3 = n4 = NULL;
//定义遍历用指针
ListNode* pcur = head;
while(pcur){
if(pcur->val < x){
//是否为空链表
if(n1 == NULL){
n1 = pcur;
n2 = n1;
}else{
n2->next = pcur;
n2 = n2->next;
}
}else{
if(n3 == NULL){
n3 = pcur;
n4 = n3;
}else{
n4->next = pcur;
n4 = n4->next;
}
}
pcur = pcur->next;
}
if(n1 == NULL){
return n3;
}else{
n2->next = n3;
if(n4){
n4->next = NULL;
}
}
return n1;
}思路二:
其实我们也可以不创建这么多的变量,我们也可以只创建一个链表,然后针对参考值对节点进行分割,然后遍历原链表,分别对节点进行尾插或头插。那么请读者思考我们该如何实现上述的思路,我给出示例代码:
cpp
typedef struct ListNode ListNode;
struct ListNode* partition(struct ListNode* head, int x) {
if (head == NULL) {
return NULL;
}
ListNode* new_head = NULL;
ListNode* small_tail = NULL;
ListNode* large_head = NULL;
ListNode* large_tail = NULL;
ListNode* pcur = head;
while (pcur != NULL) {
ListNode* next = pcur->next;
pcur->next = NULL;
if (pcur->val < x) {
if (small_tail == NULL) {
new_head = pcur;
small_tail = pcur;
} else {
small_tail->next = pcur;
small_tail = small_tail->next;
}
} else {
if (large_head == NULL) {
large_head = pcur;
large_tail = pcur;
} else {
large_tail->next = pcur;
large_tail = large_tail->next;
}
}
pcur = next;
}
if (small_tail != NULL) {
small_tail->next = large_head;
} else {
new_head = large_head;
}
return new_head;
}
那么本题到这里就结束了。
总结
本文介绍了6道经典单链表算法题目以及多种解决方法。