线性代数 - 二阶矩阵的行列式、向量叉积（Cross product）的模长与平行四边形面积的关系

线性代数 - 二阶矩阵的行列式、向量叉积（Cross product）的模长与平行四边形面积的关系

flyfish

先说结论

对于平面R2\mathbb{R}^2R2中的两个向量u=(ab)\mathbf{u} = \begin{pmatrix} a \\ b \end{pmatrix}u=(ab)和v=(cd)\mathbf{v} = \begin{pmatrix} c \\ d \end{pmatrix}v=(cd)：

它们张成的平行四边形面积 为∣底×高∣=∥u∥∥v∥∣sin⁡θ∣|\text{底} \times \text{高}| = \|\mathbf{u}\| \|\mathbf{v}\| |\sin\theta|∣底×高∣=∥u∥∥v∥∣sinθ∣（θ\thetaθ是u\mathbf{u}u与v\mathbf{v}v的夹角）。

这两个向量构成的二阶矩阵 (acbd)\begin{pmatrix} a & c \\ b & d \end{pmatrix}(abcd)的行列式 为det⁡=ad−bc\det = ad - bcdet=ad−bc，其绝对值 ∣ad−bc∣|ad - bc|∣ad−bc∣恰好等于平行四边形的面积。

开始

"Cross product" 文是叉积 （也称为向量积 或叉乘）。

R2\mathbb{R}^2R2 表示二维实数空间 ，即平面直角坐标系中的所有点，每个点由两个实数组成的有序对(x,y)(x, y)(x,y)表示。

R3\mathbb{R}^3R3 表示三维实数空间 ，即立体空间中的所有点，每个点由三个实数组成的有序组(x,y,z)(x, y, z)(x,y,z)表示

空心的R\mathbb{R}R是实数集的符号，表示包含所有有理数和无理数的集合。

Rn\mathbb{R}^nRn 就是"nnn维实数空间"，其中每个元素是nnn个实数构成的有序组，R\mathbb{R}R作为基础，定义了空间中坐标的取值范围（全体实数）。

若u\mathbf{u}u和v\mathbf{v}v是R3\mathbb{R}^3R3中的向量，则∥u×v∥\|\mathbf{u} \times \mathbf{v}\|∥u×v∥等于由u\mathbf{u}u和v\mathbf{v}v张成的平行四边形的面积 。

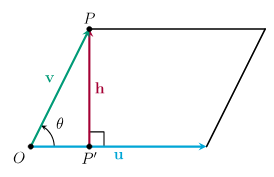
由两个向量张成的平行四边形

平行四边形的面积等于"底边长×高"。

平行四边形的底边长为∥u∥\|\mathbf{u}\|∥u∥，高为∥h∥\|\mathbf{h}\|∥h∥。

观察直角三角形OPP′OPP'OPP′，得∥h∥=∥v∥sin⁡θ\|\mathbf{h}\| = \|\mathbf{v}\| \sin\theta∥h∥=∥v∥sinθ。

因此，平行四边形的面积为∥u∥∥v∥sin⁡θ\|\mathbf{u}\| \|\mathbf{v}\| \sin\theta∥u∥∥v∥sinθ（因θ∈(0,π)\theta \in (0, \pi)θ∈(0,π)，可省略绝对值），

即等于∥u×v∥\|\mathbf{u} \times \mathbf{v}\|∥u×v∥。

若u\mathbf{u}u和v\mathbf{v}v是R3\mathbb{R}^3R3中的向量，则
∥u×v∥=∥u∥∥v∥∣sin⁡(θ)∣,\|\mathbf{u} \times \mathbf{v}\| = \|\mathbf{u}\| \|\mathbf{v}\| |\sin(\theta)|,∥u×v∥=∥u∥∥v∥∣sin(θ)∣,

其中θ\thetaθ是u\mathbf{u}u和v\mathbf{v}v之间的夹角。

原因

设u\mathbf{u}u和v\mathbf{v}v是R3\mathbb{R}^3R3中的向量，其中
u=(a1a2a3)且v=(b1b2b3).\mathbf{u} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \quad \text{且} \quad \mathbf{v} = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}.u= a1a2a3 且v= b1b2b3 .

为避免处理平方根，先计算∥u×v∥2\|\mathbf{u} \times \mathbf{v}\|^2∥u×v∥2：
∥u×v∥2=(a2b3−a3b2)2+(a3b1−a1b3)2+(a1b2−a2b1)2=(a22b32−2a2b3a3b2+a32b22)+(a32b12−2a3b1a1b3+a12b32)+(a12b22−2a1b2a2b1+a22b12)=(a12+a22+a32)(b12+b22+b32)−(a1b1+a2b2+a3b3)2=∥u∥2∥v∥2−(u⋅v)2=∥u∥2∥v∥2−(∥u∥∥v∥cos⁡(θ))2=∥u∥2∥v∥2(1−cos⁡2θ)=∥u∥2∥v∥2sin⁡2θ.\begin{align*} \|\mathbf{u} \times \mathbf{v}\|^2 &= (a_2b_3 - a_3b_2)^2 + (a_3b_1 - a_1b_3)^2 + (a_1b_2 - a_2b_1)^2 \\ &= (a_2^2b_3^2 - 2a_2b_3a_3b_2 + a_3^2b_2^2) + (a_3^2b_1^2 - 2a_3b_1a_1b_3 + a_1^2b_3^2) + (a_1^2b_2^2 - 2a_1b_2a_2b_1 + a_2^2b_1^2) \\ &= (a_1^2 + a_2^2 + a_3^2)(b_1^2 + b_2^2 + b_3^2) - (a_1b_1 + a_2b_2 + a_3b_3)^2 \\ &= \|\mathbf{u}\|^2 \|\mathbf{v}\|^2 - (\mathbf{u} \cdot \mathbf{v})^2 \\ &= \|\mathbf{u}\|^2 \|\mathbf{v}\|^2 - (\|\mathbf{u}\| \|\mathbf{v}\| \cos(\theta))^2 \\ &= \|\mathbf{u}\|^2 \|\mathbf{v}\|^2 (1 - \cos^2\theta) \\ &= \|\mathbf{u}\|^2 \|\mathbf{v}\|^2 \sin^2\theta. \end{align*}∥u×v∥2=(a2b3−a3b2)2+(a3b1−a1b3)2+(a1b2−a2b1)2=(a22b32−2a2b3a3b2+a32b22)+(a32b12−2a3b1a1b3+a12b32)+(a12b22−2a1b2a2b1+a22b12)=(a12+a22+a32)(b12+b22+b32)−(a1b1+a2b2+a3b3)2=∥u∥2∥v∥2−(u⋅v)2=∥u∥2∥v∥2−(∥u∥∥v∥cos(θ))2=∥u∥2∥v∥2(1−cos2θ)=∥u∥2∥v∥2sin2θ.

对等式两边取平方根，得
∥u×v∥=∥u∥∥v∥∣sin⁡(θ)∣,\|\mathbf{u} \times \mathbf{v}\| = \|\mathbf{u}\| \|\mathbf{v}\| |\sin(\theta)|,∥u×v∥=∥u∥∥v∥∣sin(θ)∣,

因为sin⁡2θ=∣sin⁡θ∣\sqrt{\sin^2\theta} = |\sin\theta|sin2θ =∣sinθ∣。

两个向量叉积u\mathbf{u}u和v\mathbf{v}v的模长恰好等于u\mathbf{u}u和v\mathbf{v}v张成的平行四边形的面积

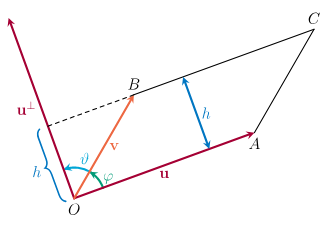
由向量u=(ab)\mathbf{u} = \begin{pmatrix} a \\ b \end{pmatrix}u=(ab)和v=(cd)\mathbf{v} = \begin{pmatrix} c \\ d \end{pmatrix}v=(cd)张成的平行四边形OACBOACBOACB的面积由∣ad−bc∣|ad - bc|∣ad−bc∣给出，即ad−bcad - bcad−bc的绝对值。

ad−bc=∥u∥∥v∥sin⁡(φ)ad - bc = \|\mathbf{u}\| \|\mathbf{v}\| \sin(\varphi)ad−bc=∥u∥∥v∥sin(φ)，其中φ\varphiφ是从u\mathbf{u}u逆时针到v\mathbf{v}v的角，我们称这个角为从u\mathbf{u}u到v\mathbf{v}v的有向角。

两个向量构成的二阶矩阵 (acbd)\begin{pmatrix} a & c \\ b & d \end{pmatrix}(abcd)的行列式 为det⁡=ad−bc\det = ad - bcdet=ad−bc，其绝对值 ∣ad−bc∣|ad - bc|∣ad−bc∣恰好等于平行四边形的面积

我们同样可以借助叉积的性质，但实际上无需提升到三维空间。通过一个小技巧，可将行列式转化为内积：
ad−bc=(a−b)⋅(cd)=u⊥⋅v,ad - bc = \begin{pmatrix} a \\ -b \end{pmatrix} \cdot \begin{pmatrix} c \\ d \end{pmatrix} = \mathbf{u}^\perp \cdot \mathbf{v},ad−bc=(a−b)⋅(cd)=u⊥⋅v,

其中u⊥\mathbf{u}^\perpu⊥是与u\mathbf{u}u垂直、指向u\mathbf{u}u左侧且长度与u\mathbf{u}u相同的向量。平行四边形OACBOACBOACB和正交向量u⊥\mathbf{u}^\perpu⊥

因此，
ad−bc=u⊥⋅v=∥u⊥∥∥v∥cos⁡(ϑ),ad - bc = \mathbf{u}^\perp \cdot \mathbf{v} = \|\mathbf{u}^\perp\| \|\mathbf{v}\| \cos(\vartheta),ad−bc=u⊥⋅v=∥u⊥∥∥v∥cos(ϑ),

其中ϑ\varthetaϑ是u⊥\mathbf{u}^\perpu⊥和v\mathbf{v}v之间的角。这里h=∥v∥cos⁡(ϑ)h = \|\mathbf{v}\| \cos(\vartheta)h=∥v∥cos(ϑ)（带正负号）是v\mathbf{v}v在u\mathbf{u}u垂线方向上的投影长度，可解释为平行四边形的高。于是：
∥u⊥∥∥v∥cos⁡(ϑ)=∥u∥∥v∥cos⁡(ϑ)=±(底边长)×高=±平行四边形OACB的面积.\begin{align*} \|\mathbf{u}^\perp\| \|\mathbf{v}\| \cos(\vartheta) &= \|\mathbf{u}\| \|\mathbf{v}\| \cos(\vartheta) \\ &= \pm (\text{底边长}) \times \text{高} \\ &= \pm \text{平行四边形}OACB\text{的面积}. \end{align*}∥u⊥∥∥v∥cos(ϑ)=∥u∥∥v∥cos(ϑ)=±(底边长)×高=±平行四边形OACB的面积.

经整理可得：
ad−bc=∥u⊥∥∥v∥cos⁡(ϑ)=∥u∥∥v∥cos⁡(π2−φ)=∥u∥∥v∥sin⁡(φ),\begin{align*} ad - bc &= \|\mathbf{u}^\perp\| \|\mathbf{v}\| \cos(\vartheta) \\ &= \|\mathbf{u}\| \|\mathbf{v}\| \cos\left(\frac{\pi}{2} - \varphi\right) \\ &= \|\mathbf{u}\| \|\mathbf{v}\| \sin(\varphi), \end{align*}ad−bc=∥u⊥∥∥v∥cos(ϑ)=∥u∥∥v∥cos(2π−φ)=∥u∥∥v∥sin(φ),

其中φ\varphiφ是从u\mathbf{u}u逆时针到v\mathbf{v}v的角。

可见，当从u\mathbf{u}u到v\mathbf{v}v的有向角小于π\piπ时，ad−bcad - bcad−bc等于平行四边形的面积；当角在π\piπ到2π2\pi2π之间时，ad−bcad - bcad−bc等于该面积的负值。我们称其为有向面积。

R2\mathbb{R}^2R2中两个向量u=(ab)\mathbf{u} = \begin{pmatrix} a \\ b \end{pmatrix}u=(ab)和v=(cd)\mathbf{v} = \begin{pmatrix} c \\ d \end{pmatrix}v=(cd)的有序对(u,v)(\mathbf{u}, \mathbf{v})(u,v)的行列式 定义为
det⁡(u,v)=ad−bc.\det(\mathbf{u}, \mathbf{v}) = ad - bc.det(u,v)=ad−bc.

或者，行列式可视为作用于2×22 \times 22×2矩阵的算子，记法为：
det⁡(u v)=det⁡((acbd))=∣acbd∣=ad−bc.\det(\mathbf{u}\ \mathbf{v}) = \det\left(\begin{pmatrix} a & c \\ b & d \end{pmatrix}\right) = \begin{vmatrix} a & c \\ b & d \end{vmatrix} = ad - bc.det(u v)=det((abcd))= abcd =ad−bc.

除面积外，行列式还能反映u\mathbf{u}u和v\mathbf{v}v的相对位置。实际上，我们可通过行列式定义平面中两个向量的定向 （后续也可定义Rn\mathbb{R}^nRn中nnn个向量的定向）。

若两个线性无关向量u\mathbf{u}u和v\mathbf{v}v的有序对(u,v)(\mathbf{u}, \mathbf{v})(u,v)满足det⁡(u,v)>0\det(\mathbf{u}, \mathbf{v}) > 0det(u,v)>0，则称其为正定向 ；若det⁡(u,v)<0\det(\mathbf{u}, \mathbf{v}) < 0det(u,v)<0，则称其为负定向。

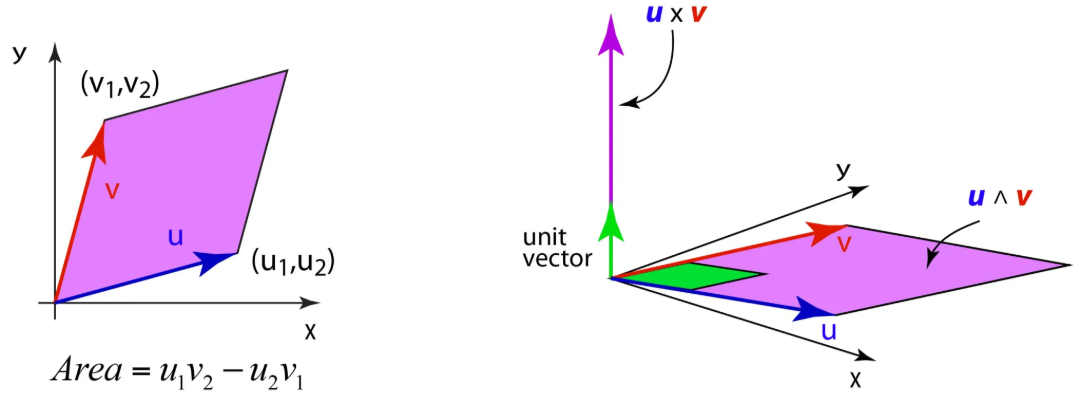
左图：二维空间的平行四边形面积（行列式/有向面积）

在二维实数空间R2\mathbb{R}^2R2中，向量u=(u1,u2)\mathbf{u} = (u_1, u_2)u=(u1,u2)和v=(v1,v2)\mathbf{v} = (v_1, v_2)v=(v1,v2)张成一个平行四边形。

其有向面积 （带符号的面积，符号反映向量的"定向"）由公式u1v2−u2v1u_1v_2 - u_2v_1u1v2−u2v1给出，这正是二阶矩阵(u1v1u2v2)\begin{pmatrix} u_1 & v_1 \\ u_2 & v_2 \end{pmatrix}(u1u2v1v2)的行列式 。

面积的绝对值就是平行四边形的实际面积

右图：三维空间的叉积与外积

在三维实数空间R3\mathbb{R}^3R3中，向量u\mathbf{u}u和v\mathbf{v}v的运算体现了"空间元素"的不同刻画：
叉积（u×v\mathbf{u} \times \mathbf{v}u×v） ：是一个向量 ，方向垂直于u\mathbf{u}u和v\mathbf{v}v所在的平面，模长 等于u\mathbf{u}u和v\mathbf{v}v张成的平行四边形的面积。图中紫色箭头的长度反映面积大小，方向体现空间垂直方向的定向。
外积（u∧v\mathbf{u} \wedge \mathbf{v}u∧v） ：是一个二维平面元素 ，直接刻画了u\mathbf{u}u和v\mathbf{v}v张成的平行四边形"本身"（包含面积和平面的定向信息）。图中紫色的平行四边形区域就是外积所表示的"平面块"，绿色小平行四边形可理解为单位化的参考。

上面提到了外积

外积（u∧v\mathbf{u} \wedge \mathbf{v}u∧v"）外积可以作为张量积（tensor product/outer product），外积也可以作为楔积（wedge product/exterior product）

叉积（u×v\mathbf{u} \times \mathbf{v}u×v）仅在三维空间 中存在，结果是一个向量 （方向垂直于原平面，模长为平行四边形面积）。

外积（u∧v\mathbf{u} \wedge \mathbf{v}u∧v）在任意nnn维空间 中都可定义，结果是一个**"2-向量"（或"二维 blade"），它直接表示u\mathbf{u}u和v\mathbf{v}v张成的平行四边形本身**（包含面积、平面的定向，以及子空间的"位置"信息）。

例子

设u\mathbf{u}u和v\mathbf{v}v是R3\mathbb{R}^3R3中的向量，其中
u=(a1a2a3)且v=(b1b2b3).\mathbf{u} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \quad \text{且} \quad \mathbf{v} = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}.u= a1a2a3 且v= b1b2b3 .
叉积 u×v\mathbf{u} \times \mathbf{v}u×v定义为
u×v=(a2b3−a3b2a3b1−a1b3a1b2−a2b1).\mathbf{u} \times \mathbf{v} = \begin{pmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{pmatrix}.u×v= a2b3−a3b2a3b1−a1b3a1b2−a2b1 .

我们来计算下列向量u\mathbf{u}u和v\mathbf{v}v的叉积。
u=(214)且v=(365).\mathbf{u} = \begin{pmatrix} 2 \\ 1 \\ 4 \end{pmatrix} \quad \text{且} \quad \mathbf{v} = \begin{pmatrix} 3 \\ 6 \\ 5 \end{pmatrix}.u= 214 且v= 365 .

根据定义，u×v\mathbf{u} \times \mathbf{v}u×v等于
(1⋅5−4⋅64⋅3−2⋅52⋅6−1⋅3)=(−1929).\begin{pmatrix} 1 \cdot 5 - 4 \cdot 6 \\ 4 \cdot 3 - 2 \cdot 5 \\ 2 \cdot 6 - 1 \cdot 3 \end{pmatrix} = \begin{pmatrix} -19 \\ 2 \\ 9 \end{pmatrix}. 1⋅5−4⋅64⋅3−2⋅52⋅6−1⋅3 = −1929 .

你可能会注意到一个特别之处：向量u×v\mathbf{u} \times \mathbf{v}u×v与u\mathbf{u}u和v\mathbf{v}v都正交 。事实上，u×v\mathbf{u} \times \mathbf{v}u×v和u\mathbf{u}u的点积为(−19)⋅2+2⋅1+9⋅4=−38+2+36=0(-19) \cdot 2 + 2 \cdot 1 + 9 \cdot 4 = -38 + 2 + 36 = 0(−19)⋅2+2⋅1+9⋅4=−38+2+36=0，u×v\mathbf{u} \times \mathbf{v}u×v和v\mathbf{v}v的点积为(−19)⋅3+2⋅6+9⋅5=−57+12+45=0(-19) \cdot 3 + 2 \cdot 6 + 9 \cdot 5 = -57 + 12 + 45 = 0(−19)⋅3+2⋅6+9⋅5=−57+12+45=0。

若u\mathbf{u}u和v\mathbf{v}v是R3\mathbb{R}^3R3中的向量，则u×v\mathbf{u} \times \mathbf{v}u×v与u\mathbf{u}u和v\mathbf{v}v都正交。

证明

设u\mathbf{u}u和v\mathbf{v}v是R3\mathbb{R}^3R3中的向量，其中
u=(a1a2a3)且v=(b1b2b3).\mathbf{u} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \quad \text{且} \quad \mathbf{v} = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}.u= a1a2a3 且v= b1b2b3 .

要证明u×v\mathbf{u} \times \mathbf{v}u×v和u\mathbf{u}u正交，需证明它们的点积为零。计算点积：
(u×v)⋅u=(a2b3−a3b2)⋅a1+(a3b1−a1b3)⋅a2+(a1b2−a2b1)⋅a3=a2b3a1−a3b2a1+a3b1a2−a1b3a2+a1b2a3−a2b1a3=0.\begin{align*} (\mathbf{u} \times \mathbf{v}) \cdot \mathbf{u} &= (a_2b_3 - a_3b_2) \cdot a_1 + (a_3b_1 - a_1b_3) \cdot a_2 + (a_1b_2 - a_2b_1) \cdot a_3 \\ &= a_2b_3a_1 - a_3b_2a_1 + a_3b_1a_2 - a_1b_3a_2 + a_1b_2a_3 - a_2b_1a_3 \\ &= 0. \end{align*}(u×v)⋅u=(a2b3−a3b2)⋅a1+(a3b1−a1b3)⋅a2+(a1b2−a2b1)⋅a3=a2b3a1−a3b2a1+a3b1a2−a1b3a2+a1b2a3−a2b1a3=0.

类似地，可证明u×v\mathbf{u} \times \mathbf{v}u×v和v\mathbf{v}v的点积也为零。