1 引言
由法国雷恩大学研究者联合完成的论文《WaterMax: Breaking the LLM Watermark Detectability--Robustness--Quality Trade-off》发表于2024年NeurIPS大会。该研究聚焦于大语言模型文本生成的可追溯性与版权保护难题,提出了一种全新的水印框架WaterMax,突破了以往检测性--鲁棒性--文本质量三者无法兼得的瓶颈。与现有通过修改 logits 或采样分布的方案不同,该方法完全不改变模型权重与采样机制,而是通过多候选文本生成与选择策略实现水印嵌入,在保持几乎无失真的文本质量下,获得了接近 100% 的检测准确率。论文不仅在理论上建立了鲁棒性与复杂度间的解析模型,还在多种主流大模型上验证了其优越性,成为当前最具代表性的高保真水印方法之一。
2 研究背景
在大语言模型文本水印的研究领域中,已有多种方法被提出以实现生成内容的可溯源性与真实性验证,例如通过修改logits分布、调整采样机制或在生成概率空间中嵌入统计信号等方式。尽管这些方法在一定程度上提升了检测准确率或降低了误报率,但普遍存在着检测性 、鲁棒性 与文本质量三者难以兼顾的内在矛盾:提高检测强度往往会导致文本自然度下降,而增强鲁棒性又可能削弱检测信号的显著性。为便于理解不同方法的设计思路与局限性,论文从多个代表性研究出发,对现有水印技术进行了系统分类与比较,具体如下表所示。
| 类别 | 代表性论文 | 核心思想 | 主要问题与局限性 |
|---|---|---|---|
| 基于概率分布修改 | A Watermark for Large Language Models | 在生成过程中对token logits加入正负偏置,使"绿色列表"token更可能被采样 | 能有效控制误报率,但强依赖文本熵,水印强度提升会显著降低文本质量 |
| 基于采样扰动 | Robust Distortion-Free Watermarks | 保持原采样分布的平均不变性,理论上"无失真" | 可检测性依赖生成熵,低熵文本检测性能差,且鲁棒性弱 |
| 统计建模与最优检测 | A Statistical Framework of Watermarks for LLMs | 从统计检验角度形式化水印嵌入与检测过程 | 提供理论界限但缺乏高质量文本的实证验证 |
| 鲁棒水印 | Robust Distortion-Free Watermarks | 设计对改写、插入、删除攻击稳定的检测器 | 鲁棒性较高但仍受限于熵水平与采样分布变化 |
| 可学习与蒸馏式水印 | On the Learnability of Watermarks for LLMs | 通过微调让模型原生生成可检测水印文本 | 训练成本高,且缺乏对失真控制的可解释性 |
| 多比特与可识别水印 | Three Bricks to Consolidate Watermarks for LLMs | 实现用户级溯源与多比特编码 | 复杂度高,易受语义改写攻击影响 |
针对现有文本水印方法在检测性、鲁棒性与质量间难以平衡的三大瓶颈,提出了基于多候选生成与最优选择的端到端水印框架,在不修改模型结构的前提下,通过近乎无失真的生成策略和可解析的鲁棒性建模,实现了跨模型、可解释且高检测率的文本水印方案,成功打破了长期存在的"检测性--鲁棒性--质量"权衡难题。
3 论文方法
该论文提出了一种全新的基于多候选生成与最优选择的语言模型文本水印方法。该方法不修改模型参数、logits或采样机制,而是通过概率统计与假设检验框架构建出可解析的水印嵌入与检测模型。以下从数学角度对其核心思想进行系统说明。
3.1 似然比统计量假设检验
设生成模型 G θ G_\theta Gθ在给定提示 P P P下生成文本 x = ( t 1 , t 2 , ... , t L ) x = (t_1, t_2, \dots, t_L) x=(t1,t2,...,tL),其中, t i t_i ti为第 i i i个token, L L L为文本长度。为区分文本是否带有水印,该方法将检测问题形式化为一个二元假设检验: H 0 H_0 H0表示文本未加水, H 1 H_1 H1表示文本带有水印文本,其检测统计量定义为似然比 Λ ( x ) = f ( x ∣ H 1 ) f ( x ∣ H 0 ) ≷ H 0 H 1 τ \Lambda(x) = \frac{f(x|H_1)}{f(x|H_0)} \mathop{\gtrless}{H_0}^{H_1} \tau Λ(x)=f(x∣H0)f(x∣H1)≷H0H1τ其中, f ( x ) f(x) f(x)表示语言模型概率输出分布, Λ ( x ) \Lambda(x) Λ(x)为似然比统计量,阈值 τ \tau τ由假阳率 P F A P{FA} PFA决定。该方法的核心思想是让模型在相同提示 P P P下生成 n n n个独立候选文本 { x 1 , x 2 , ... , x n } \{x_1, x_2, \dots, x_n\} {x1,x2,...,xn},并对每个文本计算检测得分的 p p p值 p j = P ( S ≥ s j ∣ H 0 ) p_j = P(S \ge s_j | H_0) pj=P(S≥sj∣H0)其中, S = ∑ i = 1 L u i S = \sum_{i=1}^L u_i S=∑i=1Lui为检测统计量, u i u_i ui是基于密钥 k k k对每个token哈希后生成的伪随机变量,通常取 u i ∼ N ( 0 , 1 ) u_i \sim \mathcal{N}(0,1) ui∼N(0,1)。算法最终选择 p p p值最小的候选文本 x ∗ = arg min j p j x^* = \arg\min_j p_j x∗=argjminpj作为输出。若非水印文本的 p p p值服从均匀分布 U [ 0 , 1 ] U[0,1] U[0,1],则最小值 p min p_{\min} pmin的分布为 p min ∼ Beta ( 1 , n ) p_{\min} \sim \text{Beta}(1, n) pmin∼Beta(1,n)由此可得检测功率(真阳率) P D = P ( p min < P F A ∣ H 1 ) = 1 − ( 1 − P F A ) n P_D = P(p_{\min} < P_{FA} | H_1) = 1 - (1 - P_{FA})^n PD=P(pmin<PFA∣H1)=1−(1−PFA)n该结果表明,检测性能 P D P_D PD随候选样本数 n n n 指数提升,从而显著增强水印的可检测性。
3.2 分块生成与动态选择机制
由于直接生成 n n n 个完整文本的计算代价过高,WaterMax 采用 分块生成与动态选择机制 来降低复杂度。具体而言,将目标文本划分为 N N N 个块,每个块的长度为 ℓ \ell ℓ。在生成第 i i i 个块时,模型会基于上一块的结果生成 n n n 个候选片段 { y i , 1 , . . . , y i , n } \{y_{i,1}, ..., y_{i,n}\} {yi,1,...,yi,n},并为每个候选计算累计得分:
s i , j = s i − 1 + δ s i , j , 其中 δ s i , j = ∑ k = 1 ℓ u ( i − 1 ) ℓ + k ( j ) 。 s_{i,j} = s_{i-1} + \delta s_{i,j}, \quad \text{其中 } \delta s_{i,j} = \sum_{k=1}^{\ell} u_{(i-1)\ell+k}^{(j)}。 si,j=si−1+δsi,j,其中 δsi,j=k=1∑ℓu(i−1)ℓ+k(j)。
这里, u ( i − 1 ) ℓ + k ( j ) u_{(i-1)\ell+k}^{(j)} u(i−1)ℓ+k(j) 表示第 j j j 个候选片段中第 k k k 个 token 的随机变量得分。算法在每个块上选择累计得分最大的候选片段:
y i ∗ = arg max j s i , j , y_i^* = \arg\max_j s_{i,j}, yi∗=argjmaxsi,j,
并将所有最优片段依次拼接得到最终文本:
x ∗ = [ y 1 ∗ , y 2 ∗ , ... , y N ∗ ] 。 x^* = [y_1^*, y_2^*, \dots, y_N^*]。 x∗=[y1∗,y2∗,...,yN∗]。
该机制在理论上保证了几乎无失真,同时通过局部最优选择实现了低延迟与高效率的文本生成。
3.3 最优检测器与功率分析
论文在检测阶段定义了两类关键统计量:最优检测器与鲁棒检测器。对于最优检测器,首先将每个文本块的局部 p p p值组成向量 p = ( p 1 , p 2 , . . . , p N ) p = (p_1, p_2, ..., p_N) p=(p1,p2,...,pN),并构造似然比统计量 Λ opt ( p ) = − ∑ i = 1 N log ( 1 − p i ) 。 \Lambda_{\text{opt}}(p) = -\sum_{i=1}^{N} \log(1 - p_i)。 Λopt(p)=−i=1∑Nlog(1−pi)。若各 p i p_i pi 在假设 H 1 H_1 H1 下服从 Beta ( 1 , n ) \text{Beta}(1, n) Beta(1,n) 分布,则该统计量在不同假设下满足 Λ opt ( p ) ∼ { Γ ( N , 1 ) , H 0 Γ ( N , 1 / n ) , H 1 \Lambda_{\text{opt}}(p) \sim \begin{cases}\Gamma(N, 1), & H_0 \\\Gamma(N, 1/n), & H_1\end{cases} Λopt(p)∼{Γ(N,1),Γ(N,1/n),H0H1其中, Γ ( k , θ ) \Gamma(k, \theta) Γ(k,θ) 表示形状参数为 k k k、尺度参数为 θ \theta θ的伽马分布。在给定误报率 P F A P_{FA} PFA时,其检测功率(真阳率)可表示为 P D = γ N , 1 / n ( γ N , 1 − 1 ( P F A ) ) , P_D = \gamma_{N,1/n}\!\left(\gamma_{N,1}^{-1}(P_{FA})\right), PD=γN,1/n(γN,1−1(PFA)),其中, γ a , b \gamma_{a,b} γa,b为不完全伽马函数。为提高在文本修改、删除等攻击下的鲁棒性,该论文进一步提出鲁棒检测器,将所有 token 的局部得分加总为全局统计量 Λ rob = ∑ i = 1 L u i , \Lambda_{\text{rob}} = \sum_{i=1}^L u_i, Λrob=i=1∑Lui,其中, u i u_i ui 为每个token对应的随机变量。当攻击导致部分token被修改,比例为 1 − α 1 - \alpha 1−α时,鲁棒检测器的检测功率近似为 P D ≈ Φ ( Φ − 1 ( P F A ) + α N e ( n ) 1 + α 2 ( v ( n ) − 1 ) ) , P_D \approx \Phi\!\left(\Phi^{-1}(P_{FA}) + \alpha \frac{\sqrt{N}e(n)}{\sqrt{1 + \alpha^2(v(n) - 1)}}\right), PD≈Φ(Φ−1(PFA)+α1+α2(v(n)−1) N e(n)),其中, e ( n ) e(n) e(n)与 v ( n ) v(n) v(n)分别表示最大值分布的期望与方差函数,用于刻画水印信号的强度与鲁棒性。该公式表明,鲁棒检测器的检测性能随未被攻击部分的比例 α \alpha α平滑衰减,从而在实际文本扰动下仍能保持稳定检测效果。
4 实验结果
4.1 检测性与文本质量的权衡
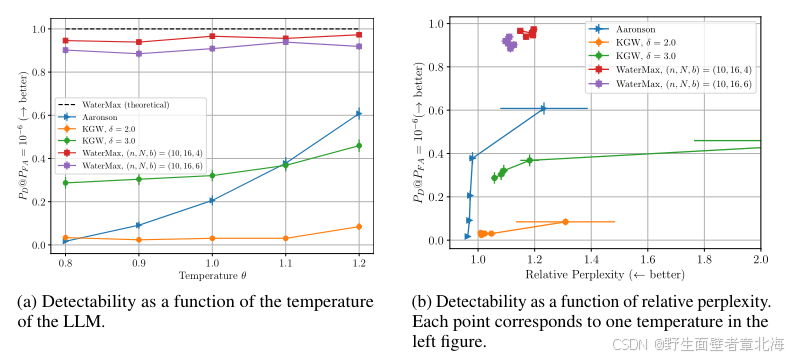
该实验旨在验证WaterMax能否同时保持高检测率与高文本质量。研究者在Llama-3-8B-Instruct模型上采用核采样(top-p=0.95)与哈希窗口大小h=6,对比了WaterMax、Aaronson与KGW三种主流水印算法在不同温度设置下的表现。实验结果显示,在固定误报率 P F A = 1 0 − 6 P_{FA}=10^{-6} PFA=10−6的条件下,WaterMax在各温度下均可实现接近1的检测率,几乎达到理论最优,同时其相对困惑度与未加水印文本基本一致,展现出近乎无失真的文本质量;相比之下,KGW需要明显牺牲文本质量才能提升检测率,而Aaronson方法仅在高温状态下表现较好。该结果充分说明 WaterMax成功突破了"检测性--质量"之间长期存在的权衡瓶颈。
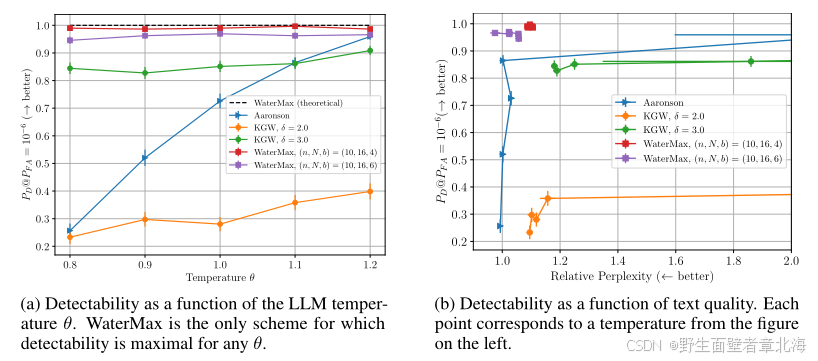
4.2 鲁棒性评估
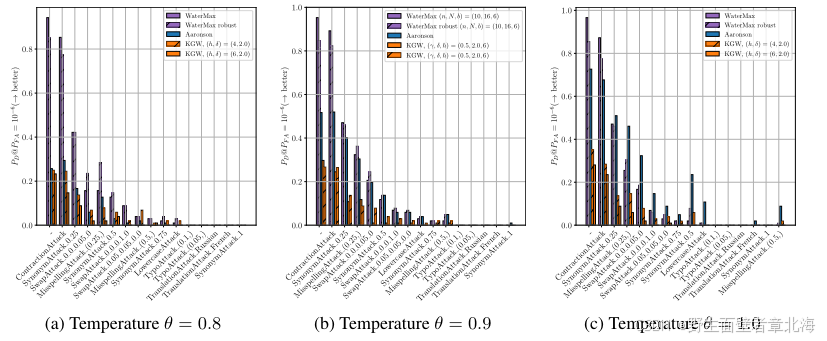
该实验的目标是评估WaterMax在多种攻击场景下的鲁棒性。研究者采用Mark My Words基准攻击集,包括同义改写、拼写扰动、单词交换、大小写变换及多语言翻译等共十余种攻击方式。在低温下对比 WaterMax、Aaronson 与KGW。结果显示,WaterMax的鲁棒检测器在同义改写、拼写扰动、单词交换等局部扰动下检测率显著高于其他方法,而在极端翻译攻击下仍保持稳定性能。实验验证了WaterMax的理论模型中提出的鲁棒检测公式,说明其在实际环境中能抵御多类语义或结构攻击。
4.3 跨模型与熵依赖分析
该实验旨在验证WaterMax 在不同语言模型和文本熵水平下的适应性与稳定性。实验结果显示,传统水印方法如KGW与Aaronson的检测性能对熵高度敏感,当模型熵较低时检测率显著下降,表现出强烈的模型依赖性。相比之下,WaterMax在不同模型与温度设置下均保持稳定且接近1的检测率,同时几乎不损失文本质量,充分说明其基于chunk的多候选生成与最优选择机制能有效利用文本熵,从而实现跨模型、跨任务的高稳健性与普适性。