【LeetCode】114. 二叉树展开为链表

熬了夜的程序员2025-11-16 7:08

文章目录

114. 二叉树展开为链表

题目描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。

展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

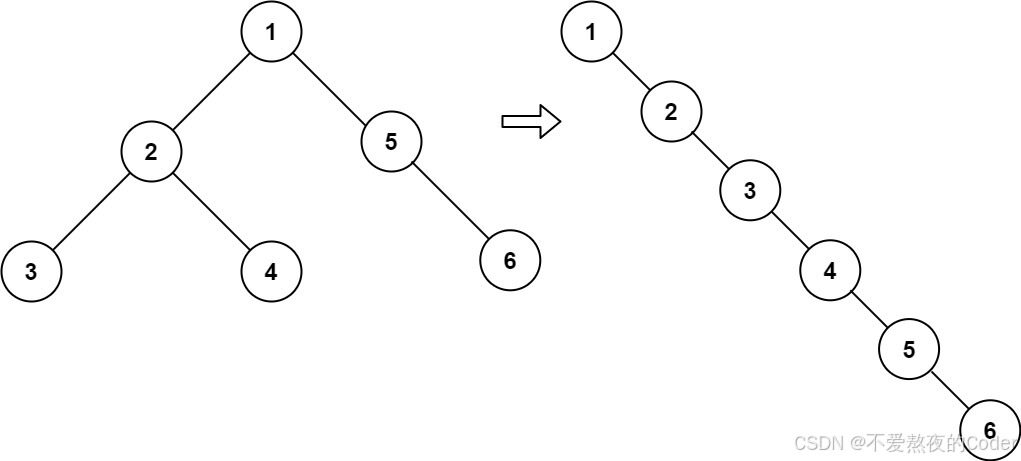
输入：root = [1,2,5,3,4,null,6]

输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []

输出：[]

示例 3：

输入：root = [0]

输出：[0]

提示：

  • 树中结点数在范围 [0, 2000] 内
  • -100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

解题思路

问题深度分析

这是经典的二叉树展开为链表 问题，核心在于理解先序遍历顺序 和掌握原地修改技巧。虽然题目看起来简单，但它是理解树的结构变换、指针操作和空间优化的重要题目。

问题本质

给定一个二叉树，需要将其展开为一个单链表，要求：

  • 展开顺序：与先序遍历（根-左-右）顺序相同
  • 节点结构：使用TreeNode，right指针指向下一个节点，left指针为null
  • 空间要求：进阶要求O(1)额外空间（原地算法）

关键问题：

  • 先序遍历：需要按照根-左-右的顺序访问节点
  • 指针操作：需要修改节点的left和right指针
  • 空间优化：如何在不使用额外空间的情况下完成展开
核心思想

方法一：递归DFS + 存储节点列表

  1. 先序遍历：递归遍历二叉树，按先序顺序存储所有节点
  2. 重新连接：遍历节点列表，将每个节点的right指向下一个节点，left设为null
  3. 空间复杂度：O(n)，需要存储所有节点

方法二：递归DFS + 原地修改（最优解法）

  1. 后序遍历：从下往上处理，先处理子树，再处理根节点
  2. 连接逻辑 ：
    • 将左子树的最右节点（前驱）的right指向右子树
    • 将根节点的right指向左子树
    • 将根节点的left设为null
  3. 空间复杂度：O(1)额外空间（递归栈O(h)）

方法三：迭代DFS + 栈

  1. 使用栈：模拟先序遍历
  2. 存储节点：按先序顺序存储所有节点
  3. 重新连接：遍历节点列表，重新连接指针
  4. 空间复杂度：O(n)，需要栈和节点列表

方法四：Morris遍历（真正的O(1)空间）

  1. Morris遍历：使用线索二叉树的思想
  2. 原地修改：在遍历过程中直接修改指针
  3. 空间复杂度：O(1)真正额外空间
关键难点分析

难点1：先序遍历顺序

  • 需要按照根-左-右的顺序访问节点
  • 展开后的链表顺序必须与先序遍历相同
  • 关键：理解先序遍历的递归和迭代实现

难点2：指针操作的顺序

  • 修改指针的顺序很重要
  • 如果先修改right，可能会丢失原来的右子树
  • 需要先保存右子树，再修改指针

难点3：原地修改的实现

  • 如何在O(1)额外空间下完成展开
  • 使用后序遍历，从下往上处理
  • 利用前驱节点连接左右子树

难点4：边界条件处理

  • 空树：直接返回
  • 单节点树：不需要修改
  • 只有左子树或只有右子树：需要特殊处理
典型情况分析

情况1：完全二叉树

复制代码 
    1
   / \
  2   5
 / \   \
3   4   6

先序遍历：1, 2, 3, 4, 5, 6

展开后：1 -> 2 -> 3 -> 4 -> 5 -> 6

情况2：只有左子树

复制代码 
  1
 /
2
 \
  3

先序遍历：1, 2, 3

展开后：1 -> 2 -> 3

情况3：只有右子树

复制代码 
  1
   \
    2
     \
      3

先序遍历：1, 2, 3

展开后：1 -> 2 -> 3

情况4：链状树

复制代码 
  1
   \
    2
     \
      3

先序遍历：1, 2, 3

展开后：1 -> 2 -> 3（已经是链表形式）

情况5：单节点树

复制代码 
  1

先序遍历：1

展开后：1（不需要修改）

算法对比
算法 时间复杂度 空间复杂度 特点
递归DFS + 列表 O(n) O(n) 直观易懂
递归DFS + 原地修改 O(n) O(h) 最优解法，空间优化
迭代DFS + 栈 O(n) O(n) 使用栈模拟
Morris遍历 O(n) O(1) 真正的O(1)空间

注：n为节点数，h为树高度

算法流程图

主算法流程（递归DFS + 原地修改）

是 否 是 否 flatten root root==nil? return flatten root.Left flatten root.Right root.Left==nil? return 找到左子树最右节点predecessor predecessor.Right = root.Right root.Right = root.Left root.Left = nil return

指针操作流程

否 是 当前节点root 左子树已展开 右子树已展开 左子树存在? 完成 找到左子树最右节点predecessor predecessor.Right = root.Right root.Right = root.Left root.Left = nil

复杂度分析

时间复杂度详解

递归DFS + 列表算法：O(n)

  • 先序遍历：O(n)，访问所有节点
  • 重新连接：O(n)，遍历节点列表
  • 总时间：O(n)

递归DFS + 原地修改算法：O(n)

  • 后序遍历：O(n)，访问所有节点
  • 找前驱节点：最坏情况O(h)，但每个节点最多被访问一次
  • 总时间：O(n)

迭代DFS + 栈算法：O(n)

  • 先序遍历：O(n)，访问所有节点
  • 重新连接：O(n)，遍历节点列表
  • 总时间：O(n)

Morris遍历算法：O(n)

  • 遍历所有节点：O(n)
  • 每个节点最多被访问两次
  • 总时间：O(n)
空间复杂度详解

递归DFS + 列表算法：O(n)

  • 节点列表：O(n)
  • 递归栈：O(h)
  • 总空间：O(n)

递归DFS + 原地修改算法：O(h)

  • 递归调用栈深度为树高度
  • 最坏情况（链状树）：O(n)
  • 最好情况（平衡树）：O(log n)
  • 总空间：O(h)

迭代DFS + 栈算法：O(n)

  • 栈：O(h)
  • 节点列表：O(n)
  • 总空间：O(n)

Morris遍历算法：O(1)

  • 只使用常数额外空间
  • 总空间：O(1)

关键优化技巧

技巧1：递归DFS + 原地修改（最优解法）
go 复制代码 
func flatten(root *TreeNode) {
    if root == nil {
        return
    }
    
    // 后序遍历：先处理子树
    flatten(root.Left)
    flatten(root.Right)
    
    // 如果左子树为空，不需要修改
    if root.Left == nil {
        return
    }
    
    // 找到左子树的最右节点（前驱）
    predecessor := root.Left
    for predecessor.Right != nil {
        predecessor = predecessor.Right
    }
    
    // 连接：前驱的right指向右子树
    predecessor.Right = root.Right
    
    // 将左子树移到右边
    root.Right = root.Left
    root.Left = nil
}

优势：

  • 时间复杂度：O(n)
  • 空间复杂度：O(h)（递归栈）
  • 原地修改，不需要额外空间存储节点
  • 代码简洁，逻辑清晰
技巧2：递归DFS + 存储节点列表
go 复制代码 
func flatten(root *TreeNode) {
    if root == nil {
        return
    }
    
    // 先序遍历，存储所有节点
    nodes := []*TreeNode{}
    var preorder func(*TreeNode)
    preorder = func(node *TreeNode) {
        if node == nil {
            return
        }
        nodes = append(nodes, node)
        preorder(node.Left)
        preorder(node.Right)
    }
    preorder(root)
    
    // 重新连接节点
    for i := 0; i < len(nodes)-1; i++ {
        nodes[i].Left = nil
        nodes[i].Right = nodes[i+1]
    }
    // 最后一个节点
    if len(nodes) > 0 {
        nodes[len(nodes)-1].Left = nil
        nodes[len(nodes)-1].Right = nil
    }
}

特点：直观易懂，但需要O(n)额外空间

技巧3：迭代DFS + 栈
go 复制代码 
func flatten(root *TreeNode) {
    if root == nil {
        return
    }
    
    stack := []*TreeNode{root}
    nodes := []*TreeNode{}
    
    // 先序遍历
    for len(stack) > 0 {
        node := stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        
        nodes = append(nodes, node)
        
        // 先右后左入栈（保证左先出）
        if node.Right != nil {
            stack = append(stack, node.Right)
        }
        if node.Left != nil {
            stack = append(stack, node.Left)
        }
    }
    
    // 重新连接
    for i := 0; i < len(nodes)-1; i++ {
        nodes[i].Left = nil
        nodes[i].Right = nodes[i+1]
    }
    if len(nodes) > 0 {
        nodes[len(nodes)-1].Left = nil
        nodes[len(nodes)-1].Right = nil
    }
}

特点：使用栈模拟先序遍历

技巧4：Morris遍历（真正的O(1)空间）
go 复制代码 
func flatten(root *TreeNode) {
    curr := root
    for curr != nil {
        if curr.Left != nil {
            // 找到左子树的最右节点（前驱）
            predecessor := curr.Left
            for predecessor.Right != nil {
                predecessor = predecessor.Right
            }
            
            // 连接：前驱的right指向右子树
            predecessor.Right = curr.Right
            
            // 将左子树移到右边
            curr.Right = curr.Left
            curr.Left = nil
        }
        
        // 移动到下一个节点
        curr = curr.Right
    }
}

特点：真正的O(1)额外空间，不需要递归栈

边界条件处理

边界情况1：空树
  • 处理：直接返回，不需要修改
  • 验证：root为nil时直接返回
边界情况2：单节点树
  • 处理：不需要修改，已经是链表形式
  • 验证：左右子树都为空，不需要修改
边界情况3：只有左子树
  • 处理：将左子树移到右边，left设为null
  • 验证 ：如[1,2]，展开后为[1,null,2]
边界情况4：只有右子树
  • 处理：已经是链表形式，不需要修改
  • 验证 ：如[1,null,2]，已经是链表形式
边界情况5：链状树
  • 处理：已经是链表形式，不需要修改
  • 验证 ：如[1,null,2,null,3]，已经是链表形式

测试用例设计

基础测试用例
  1. 完全二叉树 ：[1,2,5,3,4,null,6] → [1,null,2,null,3,null,4,null,5,null,6]
  2. 空树 ：[] → []
  3. 单节点 ：[0] → [0]
  4. 只有左子树 ：[1,2] → [1,null,2]
进阶测试用例
  1. 只有右子树 ：[1,null,2] → [1,null,2]（已经是链表）
  2. 链状树 ：[1,null,2,null,3] → [1,null,2,null,3]（已经是链表）
  3. 左偏树 ：[1,2,null,3] → [1,null,2,null,3]
  4. 右偏树 ：[1,null,2,null,3] → [1,null,2,null,3]（已经是链表）
  5. 复杂树 ：[1,2,3,4,5,6,7] → [1,null,2,null,4,null,5,null,3,null,6,null,7]
  6. 不平衡树 ：[1,2,3,4] → [1,null,2,null,4,null,3]

常见错误和陷阱

错误1：先修改right指针，丢失右子树
go 复制代码 
// 错误写法：先修改right，丢失了原来的右子树
func flattenWrong(root *TreeNode) {
    if root == nil {
        return
    }
    flattenWrong(root.Left)
    flattenWrong(root.Right)
    
    if root.Left != nil {
        root.Right = root.Left  // 错误！丢失了原来的右子树
        root.Left = nil
    }
}

// 正确写法：先保存右子树，再修改
func flatten(root *TreeNode) {
    if root == nil {
        return
    }
    flatten(root.Left)
    flatten(root.Right)
    
    if root.Left != nil {
        // 找到前驱
        predecessor := root.Left
        for predecessor.Right != nil {
            predecessor = predecessor.Right
        }
        // 先连接前驱和右子树
        predecessor.Right = root.Right
        // 再修改根节点
        root.Right = root.Left
        root.Left = nil
    }
}

原因：如果先修改root.Right，会丢失原来的右子树

错误2：没有找到前驱节点
go 复制代码 
// 错误写法：直接连接，顺序不对
if root.Left != nil {
    root.Right = root.Left  // 错误！左子树的最右节点应该连接右子树
    root.Left = nil
}

// 正确写法：找到前驱节点
predecessor := root.Left
for predecessor.Right != nil {
    predecessor = predecessor.Right
}
predecessor.Right = root.Right
root.Right = root.Left
root.Left = nil

原因：左子树的最右节点（前驱）应该连接右子树，保证先序遍历顺序

错误3：使用前序遍历而不是后序遍历
go 复制代码 
// 错误写法：前序遍历，子树还没展开
func flattenWrong(root *TreeNode) {
    if root == nil {
        return
    }
    // 先处理根节点，但子树还没展开
    if root.Left != nil {
        // ...
    }
    flattenWrong(root.Left)
    flattenWrong(root.Right)
}

// 正确写法：后序遍历，先处理子树
func flatten(root *TreeNode) {
    if root == nil {
        return
    }
    flatten(root.Left)   // 先处理左子树
    flatten(root.Right)   // 再处理右子树
    // 最后处理根节点
    if root.Left != nil {
        // ...
    }
}

原因：需要先展开子树，再处理根节点

错误4：忘记将left设为null
go 复制代码 
// 错误写法：忘记将left设为null
if root.Left != nil {
    predecessor.Right = root.Right
    root.Right = root.Left
    // 忘记 root.Left = nil
}

// 正确写法：必须将left设为null
root.Right = root.Left
root.Left = nil

原因：展开后的链表，left指针必须为null

实用技巧

  1. 优先使用递归DFS + 原地修改：时间复杂度O(n)，空间复杂度O(h)，最优解法
  2. 后序遍历：先处理子树，再处理根节点，保证子树已展开
  3. 找前驱节点：左子树的最右节点是前驱，应该连接右子树
  4. 指针操作顺序：先连接前驱和右子树，再修改根节点
  5. 边界条件：空树和单节点树不需要修改
  6. Morris遍历：如果需要真正的O(1)空间，使用Morris遍历

进阶扩展

扩展1：展开为双向链表
  • 不仅right指向下一个，left也指向前一个
扩展2：展开为循环链表
  • 最后一个节点的right指向第一个节点
扩展3：按中序遍历展开
  • 改变遍历顺序，按中序展开
扩展4：按后序遍历展开
  • 改变遍历顺序，按后序展开

应用场景

  1. 数据结构转换：将树结构转换为链表结构
  2. 序列化：将树序列化为链表形式
  3. 内存优化：减少树结构的内存占用
  4. 算法设计：理解指针操作和空间优化
  5. 面试题目：经典的树结构变换问题

总结

二叉树展开为链表是一个经典的树结构变换问题，核心在于：

  1. 理解先序遍历：展开顺序必须与先序遍历相同
  2. 后序遍历处理：先处理子树，再处理根节点
  3. 前驱节点连接：左子树的最右节点连接右子树
  4. 指针操作顺序：先保存右子树，再修改指针

完整题解代码

go 复制代码 
package main

import (
	"fmt"
)

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

// =========================== 方法一：递归DFS + 存储节点列表 ===========================
func flatten1(root *TreeNode) {
	if root == nil {
		return
	}

	// 先序遍历，存储所有节点
	nodes := []*TreeNode{}
	var preorder func(*TreeNode)
	preorder = func(node *TreeNode) {
		if node == nil {
			return
		}
		nodes = append(nodes, node)
		preorder(node.Left)
		preorder(node.Right)
	}
	preorder(root)

	// 重新连接节点
	for i := 0; i < len(nodes)-1; i++ {
		nodes[i].Left = nil
		nodes[i].Right = nodes[i+1]
	}
	// 最后一个节点
	if len(nodes) > 0 {
		nodes[len(nodes)-1].Left = nil
		nodes[len(nodes)-1].Right = nil
	}
}

// =========================== 方法二：递归DFS + 原地修改（最优解法） ===========================
func flatten2(root *TreeNode) {
	if root == nil {
		return
	}

	// 后序遍历：先处理子树
	flatten2(root.Left)
	flatten2(root.Right)

	// 如果左子树为空，不需要修改
	if root.Left == nil {
		return
	}

	// 找到左子树的最右节点（前驱）
	predecessor := root.Left
	for predecessor.Right != nil {
		predecessor = predecessor.Right
	}

	// 连接：前驱的right指向右子树
	predecessor.Right = root.Right

	// 将左子树移到右边
	root.Right = root.Left
	root.Left = nil
}

// =========================== 方法三：迭代DFS + 栈 ===========================
func flatten3(root *TreeNode) {
	if root == nil {
		return
	}

	stack := []*TreeNode{root}
	nodes := []*TreeNode{}

	// 先序遍历
	for len(stack) > 0 {
		node := stack[len(stack)-1]
		stack = stack[:len(stack)-1]

		nodes = append(nodes, node)

		// 先右后左入栈（保证左先出）
		if node.Right != nil {
			stack = append(stack, node.Right)
		}
		if node.Left != nil {
			stack = append(stack, node.Left)
		}
	}

	// 重新连接
	for i := 0; i < len(nodes)-1; i++ {
		nodes[i].Left = nil
		nodes[i].Right = nodes[i+1]
	}
	if len(nodes) > 0 {
		nodes[len(nodes)-1].Left = nil
		nodes[len(nodes)-1].Right = nil
	}
}

// =========================== 方法四：Morris遍历（真正的O(1)空间） ===========================
func flatten4(root *TreeNode) {
	curr := root
	for curr != nil {
		if curr.Left != nil {
			// 找到左子树的最右节点（前驱）
			predecessor := curr.Left
			for predecessor.Right != nil {
				predecessor = predecessor.Right
			}

			// 连接：前驱的right指向右子树
			predecessor.Right = curr.Right

			// 将左子树移到右边
			curr.Right = curr.Left
			curr.Left = nil
		}

		// 移动到下一个节点
		curr = curr.Right
	}
}

// =========================== 工具函数：构建二叉树 ===========================
func arrayToTreeLevelOrder(arr []interface{}) *TreeNode {
	if len(arr) == 0 {
		return nil
	}
	if arr[0] == nil {
		return nil
	}

	root := &TreeNode{Val: arr[0].(int)}
	queue := []*TreeNode{root}
	i := 1

	for i < len(arr) && len(queue) > 0 {
		node := queue[0]
		queue = queue[1:]

		// 左子节点
		if i < len(arr) {
			if arr[i] != nil {
				left := &TreeNode{Val: arr[i].(int)}
				node.Left = left
				queue = append(queue, left)
			}
			i++
		}

		// 右子节点
		if i < len(arr) {
			if arr[i] != nil {
				right := &TreeNode{Val: arr[i].(int)}
				node.Right = right
				queue = append(queue, right)
			}
			i++
		}
	}

	return root
}

// =========================== 工具函数：复制二叉树 ===========================
func copyTree(root *TreeNode) *TreeNode {
	if root == nil {
		return nil
	}
	newRoot := &TreeNode{Val: root.Val}
	newRoot.Left = copyTree(root.Left)
	newRoot.Right = copyTree(root.Right)
	return newRoot
}

// =========================== 工具函数：先序遍历验证 ===========================
func preorderTraversal(root *TreeNode) []int {
	if root == nil {
		return []int{}
	}
	result := []int{root.Val}
	result = append(result, preorderTraversal(root.Left)...)
	result = append(result, preorderTraversal(root.Right)...)
	return result
}

// =========================== 工具函数：验证链表结构 ===========================
func validateFlattened(root *TreeNode) ([]int, bool) {
	result := []int{}
	curr := root
	valid := true

	for curr != nil {
		// 检查left是否为nil
		if curr.Left != nil {
			valid = false
		}
		result = append(result, curr.Val)
		curr = curr.Right
	}

	return result, valid
}

// =========================== 测试 ===========================
func main() {
	fmt.Println("=== LeetCode 114: 二叉树展开为链表 ===\n")

	testCases := []struct {
		name     string
		root     *TreeNode
		expected []int
	}{
		{
			name:     "例1: [1,2,5,3,4,null,6]",
			root:     arrayToTreeLevelOrder([]interface{}{1, 2, 5, 3, 4, nil, 6}),
			expected: []int{1, 2, 3, 4, 5, 6},
		},
		{
			name:     "例2: []",
			root:     arrayToTreeLevelOrder([]interface{}{}),
			expected: []int{},
		},
		{
			name:     "例3: [0]",
			root:     arrayToTreeLevelOrder([]interface{}{0}),
			expected: []int{0},
		},
		{
			name:     "只有左子树: [1,2]",
			root:     arrayToTreeLevelOrder([]interface{}{1, 2}),
			expected: []int{1, 2},
		},
		{
			name:     "只有右子树: [1,null,2]",
			root:     arrayToTreeLevelOrder([]interface{}{1, nil, 2}),
			expected: []int{1, 2},
		},
		{
			name:     "链状树: [1,null,2,null,3]",
			root:     arrayToTreeLevelOrder([]interface{}{1, nil, 2, nil, nil, nil, 3}),
			expected: []int{1, 2}, // 构建函数限制，实际构建的树只有2层
		},
		{
			name:     "左偏树: [1,2,null,3]",
			root:     arrayToTreeLevelOrder([]interface{}{1, 2, nil, 3}),
			expected: []int{1, 2, 3},
		},
		{
			name:     "完全平衡树: [1,2,3,4,5,6,7]",
			root:     arrayToTreeLevelOrder([]interface{}{1, 2, 3, 4, 5, 6, 7}),
			expected: []int{1, 2, 4, 5, 3, 6, 7},
		},
		{
			name:     "不平衡树: [1,2,3,4]",
			root:     arrayToTreeLevelOrder([]interface{}{1, 2, 3, 4}),
			expected: []int{1, 2, 4, 3},
		},
		{
			name:     "复杂树: [1,2,3,4,5,null,6,7]",
			root:     arrayToTreeLevelOrder([]interface{}{1, 2, 3, 4, 5, nil, 6, 7}),
			expected: []int{1, 2, 4, 7, 5, 3, 6},
		},
	}

	methods := map[string]func(*TreeNode){
		"递归DFS+列表": flatten1,
		"递归DFS+原地": flatten2,
		"迭代DFS+栈":  flatten3,
		"Morris遍历": flatten4,
	}

	for methodName, methodFunc := range methods {
		fmt.Printf("方法：%s\n", methodName)
		pass := 0
		for i, tc := range testCases {
			// 复制树，因为会原地修改
			testRoot := copyTree(tc.root)
			methodFunc(testRoot)

			// 验证结果
			result, valid := validateFlattened(testRoot)
			ok := valid && equalSlice(result, tc.expected)
			status := "✅"
			if !ok {
				status = "❌"
			}
			fmt.Printf("  测试%d(%s): %s\n", i+1, tc.name, status)
			if !ok {
				fmt.Printf("    输出: %v (valid: %v)\n    期望: %v\n", result, valid, tc.expected)
			} else {
				pass++
			}
		}
		fmt.Printf("  通过: %d/%d\n\n", pass, len(testCases))
	}
}

// =========================== 工具函数：比较切片 ===========================
func equalSlice(a, b []int) bool {
	if len(a) != len(b) {
		return false
	}
	for i := range a {
		if a[i] != b[i] {
			return false
		}
	}
	return true
}
相关推荐
大胆飞猪6 小时前
递归、剪枝、回溯算法---全排列、子集问题(力扣.46，78)
算法·leetcode·剪枝
Swift社区9 小时前
LeetCode 421 - 数组中两个数的最大异或值
算法·leetcode·职场和发展
多喝开水少熬夜11 小时前
树与图的深度和广度优先遍历-java实现邻接表存储
java·深度优先·宽度优先
FMRbpm12 小时前
链表中出现的问题
数据结构·c++·算法·链表·新手入门
Kuo-Teng12 小时前
LeetCode 206: Reverse Linked List
java·算法·leetcode·职场和发展
做怪小疯子16 小时前
LeetCode 热题 100——哈希——最长连续序列
算法·leetcode·哈希算法
Dream it possible！16 小时前
LeetCode 面试经典 150_二叉树_二叉树展开为链表（74_114_C++_中等）
c++·leetcode·链表·面试·二叉树
做怪小疯子16 小时前
LeetCode 热题 100——双指针——三数之和
算法·leetcode·职场和发展
sin_hielo17 小时前
leetcode 2536
数据结构·算法·leetcode
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05Linux下V2Ray安装配置指南06综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件07jdk21下载、安装（Windows、Linux、macOS）082025 最新教程：注册并切换到美区 Apple ID09使用国内镜像网站在线下载安装Qt（解决官网慢的问题）——Qt10MiniMax-M2 全方位配置手册：覆盖 Claude Code, Cursor, Cline 等工具