算法场景:二分查找在「峰值问题」中的经典应用
在学习二分查找时,很多初学者都会产生疑问:
二分查找只能用来找"某个具体值"吗?
答案是否定的。
二分查找的本质,是在"有规律的区间"中不断缩小搜索范围。
本篇文章将通过两道非常经典的「峰值问题」,带你真正理解 二分查找在算法中的灵活应用 。


- 算法场景:二分查找在「峰值问题」中的经典应用
- 目录
-
- 一、山脉数组的峰顶索引
-
- [1.1 题目链接](#1.1 题目链接)
- [1.2 题目描述](#1.2 题目描述)
- [1.3 题目示例](#1.3 题目示例)
- [1.4 算法思路](#1.4 算法思路)
-
- [1️⃣ 为什么可以用二分查找?](#1️⃣ 为什么可以用二分查找?)
- [2️⃣ 如何判断?](#2️⃣ 如何判断?)
- [3️⃣ 边界为什么从 1 到 n-2?](#3️⃣ 边界为什么从 1 到 n-2?)
- [1.5 核心代码(C++)](#1.5 核心代码(C++))
- [1.6 示例测试(思路演示)](#1.6 示例测试(思路演示))
- 二、寻找峰值元素
-
- [2.1 题目链接](#2.1 题目链接)
- [2.2 题目描述](#2.2 题目描述)
- [2.3 题目示例](#2.3 题目示例)
- [2.4 算法思路](#2.4 算法思路)
-
- [1️⃣ 核心观察](#1️⃣ 核心观察)
- [2.5 核心代码(C++)](#2.5 核心代码(C++))
- [2.6 示例测试(思路演示)](#2.6 示例测试(思路演示))
- 总结
目录
一、山脉数组的峰顶索引
1.1 题目链接
1.2 题目描述
给定一个 山脉数组 arr,满足:
arr.length >= 3- 数组先严格递增,再严格递减
- 峰顶元素既不是第一个,也不是最后一个
请你返回峰顶元素的索引。
1.3 题目示例
输入:arr = [0,2,4,3,1]
输出:2
解释:4 是数组中的最大值,对应索引为 21.4 算法思路
1️⃣ 为什么可以用二分查找?
山脉数组具备明确的单调性规律:
- 峰顶左侧:递增
- 峰顶右侧:递减
我们不需要完整遍历数组,只需判断:
- 当前
mid是在上坡还是下坡
2️⃣ 如何判断?
比较:
arr[mid] 和 arr[mid - 1]arr[mid] > arr[mid - 1]👉 在上坡,峰顶在右侧arr[mid] < arr[mid - 1]👉 在下坡,峰顶在左侧(含 mid)
3️⃣ 边界为什么从 1 到 n-2?
因为题目保证:
- 峰顶不可能是第一个或最后一个元素
- 避免
mid-1越界
1.5 核心代码(C++)
cpp
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left = 1; // 跳过起始位置
int right = arr.size() - 2; // 跳过末尾位置
while (left < right) {
int mid = left + (right - left + 1) / 2;
if (arr[mid] > arr[mid - 1])
left = mid; // 在上坡,峰顶在右侧
else
right = mid - 1; // 在下坡,峰顶在左侧
}
return left;
}
};1.6 示例测试(思路演示)
以 [0,2,4,3,1] 为例:
- mid = 2 →
4 > 2👉 上坡 - left 移到 2
- 最终 left == right == 2,返回答案
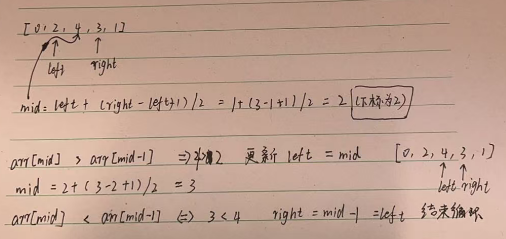
二、寻找峰值元素
2.1 题目链接
👉 https://leetcode.cn/problems/find-peak-element/description/
2.2 题目描述
给定一个数组 nums,峰值元素是指:
nums[i] > nums[i-1] 且 nums[i] > nums[i+1]你可以假设:
nums[-1] = nums[n] = -∞- 数组中 可能有多个峰值
- 返回任意一个即可
2.3 题目示例
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素2.4 算法思路
1️⃣ 核心观察
比较:
nums[mid] 和 nums[mid + 1]-
nums[mid] > nums[mid + 1]👉 说明左侧存在峰值(可能是 mid)
-
nums[mid] < nums[mid + 1]👉 说明右侧一定存在峰值
这是因为数组两端被视作 -∞,峰值一定存在
2.5 核心代码(C++)
cpp
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[mid + 1])
right = mid; // 峰值在左侧
else
left = mid + 1; // 峰值在右侧
}
return left;
}
};2.6 示例测试(思路演示)
以 [1,2,3,1] 为例:
- mid = 1 →
2 < 3👉 右侧有峰值 - left = 2
- 最终返回索引 2

总结
在本篇文章中,我们通过 「山脉数组的峰顶索引」 与 「寻找峰值元素」 两道经典题目,深入理解了:
-
二分查找 不只是查找某个数
-
而是用于 在有规律的区间中缩小答案范围
-
关键在于:
- 找到单调性
- 明确比较对象
- 正确收缩区间
✨ 坚持用 清晰易懂的图解 + 代码语言, 让每个知识点都 简单直观 !
🚀 个人主页 :不呆头 · CSDN
🌱 代码仓库 :不呆头 · Gitee
📌 专栏系列 :
💬 座右铭 : "不患无位,患所以立。"
