偏导数和全导数的个人理解

作为偏导数和全导数的笔记，方便理解与复习。

最近在看论文的时候，原理部分多次提到了梯度算子 ∇\nabla∇，但是早把梯度什么的忘完了，AI一搜说是偏导数，但是深度学习里的梯度算子还不太一样，有些是全导数，有些是偏导数，搞得我头疼，最后终于总结出了一个比较合理的解释，所以记下笔记。

另外，由于基础理论是由AI来的，所以总结说法不一定准确。

一.导数、偏导数、全导数和梯度

1.导数

设函数 y=f(x)y = f(x)y=f(x) 在点 x0x_0x0 的某个邻域内有定义。当自变量 xxx 在 x0x_0x0 处取得增量 Δx\Delta xΔx（点 x0+Δxx_0 + \Delta xx0+Δx 仍在该邻域内）时，函数取得增量 Δy=f(x0+Δx)−f(x0)\Delta y = f(x_0 + \Delta x) - f(x_0)Δy=f(x0+Δx)−f(x0)。如果增量之比 ΔyΔx\frac{\Delta y}{\Delta x}ΔxΔy 当 Δx→0\Delta x \to 0Δx→0 时的极限存在，则称函数在 x0x_0x0 处可导，并称这个极限为函数在 x0x_0x0 处的导数，记作 f′(x0)f'(x_0)f′(x0)、y′∣x=x0y'|{x=x_0}y′∣x=x0 或 dydx∣x=x0\frac{dy}{dx}|{x=x_0}dxdy∣x=x0。
f′(x0)=lim⁡Δx→0ΔyΔx=lim⁡Δx→0f(x0+Δx)−f(x0)Δx f'(x_0) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} f′(x0)=Δx→0limΔxΔy=Δx→0limΔxf(x0+Δx)−f(x0)PS：设 δ\deltaδ 是一个正数（δ>0\delta > 0δ>0），点 a∈Ra \in \mathbb{R}a∈R。那么点 aaa 的 δ\deltaδ 邻域 是指满足以下不等式的所有实数 xxx 的集合：
{x∈R∣∣x−a∣<δ} \{ x \in \mathbb{R} \mid |x - a| < \delta \} {x∈R∣∣x−a∣<δ}用区间表示就是：(a−δ,a+δ)(a - \delta, a + \delta)(a−δ,a+δ)。

2.偏导数

简单来说，偏导数是"在多变量函数中，只让一个变量变化，其他变量固定不动时的导数"。

以二元函数为例，设函数 z=f(x,y)z = f(x, y)z=f(x,y) 在点 (x0,y0)(x_0, y_0)(x0,y0) 的某个邻域内有定义。

对 xxx 的偏导数：

过程：固定 y=y0y = y_0y=y0，将 f(x,y)f(x, y)f(x,y) 视为关于 xxx 的一元函数 g(x)=f(x,y0)g(x) = f(x, y_0)g(x)=f(x,y0)。
然后对这个一元函数在 x0x_0x0 处求普通导数，这个导数就是 fff 在点 (x0,y0)(x_0, y_0)(x0,y0) 处对 xxx 的偏导数。
数学定义（极限形式） ：
∂f∂x∣(x0,y0)=lim⁡Δx→0f(x0+Δx,y0)−f(x0,y0)Δx \frac{\partial f}{\partial x}\bigg|{(x_0, y_0)} = \lim{\Delta x \to 0} \frac{f(x_0 + \Delta x, y_0) - f(x_0, y_0)}{\Delta x} ∂x∂f (x0,y0)=Δx→0limΔxf(x0+Δx,y0)−f(x0,y0)
常用符号 ：∂f∂x,fx,∂xf\frac{\partial f}{\partial x}, \quad f_x, \quad \partial_x f∂x∂f,fx,∂xf。在点 (x0,y0)(x_0, y_0)(x0,y0) 处的值记为 fx(x0,y0)f_x(x_0, y_0)fx(x0,y0)。

对其他自变量的偏导数同理。

偏导数在数学定义上是不考虑自变量之间的关系的，所以严格意义上，无论自变量间有什么函数关系，在对某个自变量求偏导的时候都会将其他的自变量视为常数。

例如：

设函数 z=f(x,y)z = f(x, y)z=f(x,y) 在点 (x0,y0)(x_0, y_0)(x0,y0) 的某个邻域内有定义，且 y=g(x)y=g(x)y=g(x)，此时，即便 yyy 是关于 xxx 的一个函数，zzz 对 xxx 的偏导数还是与之前的例子一模一样。当然，如果 xxx 是 yyy 的一个函数，即 x=g(y)x=g(y)x=g(y)，也是一样的情况。

3.全导数

在实际情况中，自变量之间往往会存在一定的关系，偏导数的定义就决定了它不会利用这个关系，所以我们需要全导数来解决这个问题。

全导数与偏导数一样都是针对多元函数，但是在定义和记号上有所不同。

简单来说，全导数是"在多变量函数中，所有自变量都沿某个路径变化时，函数值关于该路径参数的总变化率"。

以二元函数为例，设函数 z=f(x,y)z = f(x, y)z=f(x,y)，而 xxx 和 yyy 又是另一个变量 ttt 的函数，即 x=x(t), y=y(t)x = x(t),\ y = y(t)x=x(t), y=y(t)，那么 zzz 通过中间变量 x,yx, yx,y 最终成为 ttt 的一元函数。

对 ttt 的全导数：

过程：考虑 ttt 有一个微小变化 Δt\Delta tΔt，这会引起 xxx 和 yyy 分别变化 Δx\Delta xΔx 和 Δy\Delta yΔy，进而导致 zzz 变化 Δz\Delta zΔz。全导数描述的是 zzz 关于 ttt 的瞬时变化率。
数学定义（极限形式） ：
dzdt=lim⁡Δt→0ΔzΔt \frac{dz}{dt} = \lim_{\Delta t \to 0} \frac{\Delta z}{\Delta t} dtdz=Δt→0limΔtΔz其中 Δz=f(x(t+Δt),y(t+Δt))−f(x(t),y(t))\Delta z = f(x(t+\Delta t), y(t+\Delta t)) - f(x(t), y(t))Δz=f(x(t+Δt),y(t+Δt))−f(x(t),y(t))。
链式法则（计算公式） ：
通过函数的偏导数和中间变量对 ttt 的导数来计算：
dzdt=∂f∂x⋅dxdt+∂f∂y⋅dydt \frac{dz}{dt} = \frac{\partial f}{\partial x} \cdot \frac{dx}{dt} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dt} dtdz=∂x∂f⋅dtdx+∂y∂f⋅dtdy这里 ∂f∂x\frac{\partial f}{\partial x}∂x∂f 和 ∂f∂y\frac{\partial f}{\partial y}∂y∂f 在点 (x(t),y(t))(x(t), y(t))(x(t),y(t)) 处取值。
该式子可以看出，全导数是原函数对所有中间变量的偏导数与中间变量对 ttt 的全导数的乘积的和。

几何/物理意义 ：全导数 dzdt\frac{dz}{dt}dtdz 反映了当参数 ttt 变化时，函数值 zzz 沿着由 (x(t),y(t))(x(t), y(t))(x(t),y(t)) 确定的路径变化的总体速率。它是各个方向变化分量的线性叠加。

全导数在数学定义上将原函数的所有自变量都当成了中间变量，把它们看作同一个自变量 ttt 的函数（如果存在）。

举个更极端的例子：

设函数 z=f(x,y)z = f(x, y)z=f(x,y)，而 xxx 是 yyy 的函数，即 x=g(y)x = g(y)x=g(y)，那么把 xxx 看成最终自变量 ttt 的情况下，yyy 应该被表示为 y=g−1(x)y=g^{-1}(x)y=g−1(x) 也就是函数 ggg 的反函数 g−1g^{-1}g−1，然后按照同样的过程按照链式法则求得最终的全导数。当然，如果 yyy 与 xxx 完全没关系，它不随 xxx 的变化而变化，那么它就会被视为常数。

4.梯度

简单来说，梯度是一个向量，它指示了"在多变量函数中，函数值增长最快的方向"，其大小（模长）代表了该方向上的最大增长率。

其实就是存储了原函数对每个自变量的偏导数的一个向量。

以二元函数为例，设函数 z=f(x,y)z = f(x, y)z=f(x,y) 在点 P0(x0,y0)P_0(x_0, y_0)P0(x0,y0) 的某个邻域内所有一阶偏导数都存在。

梯度：

过程：将函数在该点处对所有自变量的偏导数作为分量，组合成一个向量。这个向量就是函数在该点的梯度。
数学定义（在直角坐标系下） ：
函数 f(x,y)f(x, y)f(x,y) 在点 (x0,y0)(x_0, y_0)(x0,y0) 处的梯度是一个向量，定义为：
∇f(x0,y0)=(∂f∂x(x0,y0), ∂f∂y(x0,y0)) \nabla f(x_0, y_0) = \left( \frac{\partial f}{\partial x}(x_0, y_0),\ \frac{\partial f}{\partial y}(x_0, y_0) \right) ∇f(x0,y0)=(∂x∂f(x0,y0), ∂y∂f(x0,y0))
常用符号 ：∇f\nabla f∇f，有时也记为 grad f\text{grad}\ fgrad f。它是一个向量值函数。

方向导数关系 ：

梯度最核心的性质是，函数 fff 在点 P0P_0P0 处沿任意单位向量 u=(u1,u2)\mathbf{u} = (u_1, u_2)u=(u1,u2) 的方向导数，等于该点的梯度与方向向量 u\mathbf{u}u 的点积：
Duf(P0)=∇f(P0)⋅u=∂f∂x(P0)⋅u1+∂f∂y(P0)⋅u2 D_{\mathbf{u}} f(P_0) = \nabla f(P_0) \cdot \mathbf{u} = \frac{\partial f}{\partial x}(P_0)\cdot u_1 + \frac{\partial f}{\partial y}(P_0) \cdot u_2 Duf(P0)=∇f(P0)⋅u=∂x∂f(P0)⋅u1+∂y∂f(P0)⋅u2从这个关系可以直接推出：

梯度方向 ∇f∥∇f∥\frac{\nabla f}{\|\nabla f\|}∥∇f∥∇f 是函数值增加最快的方向，该方向的方向导数等于梯度的模长 ∥∇f∥\|\nabla f\|∥∇f∥。
与梯度垂直的方向，方向导数为零，即该方向是函数的"等高线/等值面"方向。
梯度的反方向 −∇f-\nabla f−∇f 是函数值下降最快的方向，这在优化算法（如梯度下降法）中至关重要。

几何意义：梯度向量垂直于函数在该点的等值线（或等值面），并指向函数值更高的区域。

从数学定义上来看，梯度是严格意义上的偏导数的向量，而不是全导数的向量。

二、深度学习里的"潜规则"

因为在深度学习中，模型的参数更新是利用自动微分系统实现的，所以理论分析时习惯上称为梯度，但是自动微分系统实际计算的是叶节点对目标函数的导数，它可能等于数学上的偏导数，也可能是全导数，具体取决于计算图结构。

1. 自动微分系统

自动微分系统是深度学习的核心引擎，它通过计算图 和链式法则 自动计算导数。它有两种模式：

前向模式：从输入到输出逐层计算导数
反向模式：从输出到输入反向传播（深度学习主要使用此模式）

示例：
u(x)=x2F(u)=2u u(x) = x^2 \\ F(u) = 2u u(x)=x2F(u)=2u计算图：
x→u→F x \rightarrow u \rightarrow F x→u→F前向过程：

步骤1 ：
- x→ux \rightarrow ux→u，通过 xxx 计算 uuu
步骤2 ：
- u→Fu \rightarrow Fu→F，通过 uuu 计算 FFF

反向过程：

步骤1 （对应前向步骤2）：
- u→Fu \rightarrow Fu→F，计算 ∂F∂u\frac{\partial F}{\partial u}∂u∂F
步骤2 （对应前向步骤1）：
- x→ux \rightarrow ux→u，计算 ∂u∂x\frac{\partial u}{\partial x}∂x∂u

在这个简单链式结构中，系统计算的导数恰好对应数学上的偏导数。

2. 按层遍历

自动微分支持在一个步骤中计算多个偏导数。

示例：
u(x,y)=x+y2F(u)=2u u(x,y) = x + y^2 \\ F(u) = 2u u(x,y)=x+y2F(u)=2u计算图：

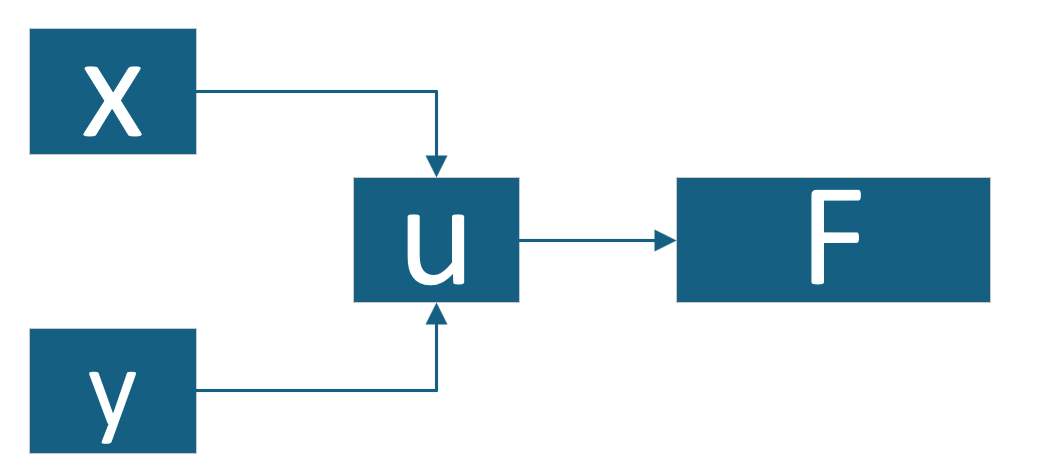
前向过程：

步骤1 ：
- x→ux \rightarrow ux→u：通过 xxx 计算 uuu
- y→uy \rightarrow uy→u：通过 yyy 计算 uuu
步骤2 ：
- u→Fu \rightarrow Fu→F，通过 uuu 计算 FFF

反向过程：

步骤1 ：
- u→Fu \rightarrow Fu→F，计算 ∂F∂u\frac{\partial F}{\partial u}∂u∂F
步骤2 ：
- x→ux \rightarrow ux→u，计算 ∂u∂x\frac{\partial u}{\partial x}∂x∂u
- y→uy \rightarrow uy→u，计算 ∂u∂y\frac{\partial u}{\partial y}∂y∂u

系统在一个反向步骤中同时计算了 xxx 和 yyy 的偏导数。

3. 反向模式的按需计算梯度

反向模式的一个重要特性是按需计算：只计算用户请求的梯度，不计算不必要的中间梯度。

当变量在计算图中存在依赖关系时，按需计算机制返回的"梯度"实际上是全导数，而非数学定义中的偏导数。
示例：
b(a)=2aF(a,b)=a+b b(a) = 2a \\ F(a,b) = a + b b(a)=2aF(a,b)=a+b计算图：

前向过程：

步骤1 ：
- a→ba \rightarrow ba→b：计算 bbb
- a→Fa \rightarrow Fa→F：为 FFF 提供 aaa
步骤2 ：
- b→Fb \rightarrow Fb→F：为 FFF 提供 bbb
- 计算 F(a,b)F(a,b)F(a,b)

反向过程：

步骤1 ：
- b→Fb \rightarrow Fb→F，计算 ∂F∂b\frac{\partial F}{\partial b}∂b∂F
步骤2 ：
- a→ba \rightarrow ba→b，计算 ∂b∂a\frac{\partial b}{\partial a}∂a∂b
- a→Fa \rightarrow Fa→F，计算 ∂F∂a\frac{\partial F}{\partial a}∂a∂F

按需计算的效果：

计算 ∂F∂b\frac{\partial F}{\partial b}∂b∂F 时
- 只需执行反向步骤1
- 得到：∂F∂b=1\frac{\partial F}{\partial b} = 1∂b∂F=1（偏导数）
计算 ∂F∂a\frac{\partial F}{\partial a}∂a∂F 时
- 需要执行反向步骤1和2
- 系统自动合并两条路径的贡献：
  - 直接路径：∂F∂a=1\frac{\partial F}{\partial a} = 1∂a∂F=1
  - 间接路径：∂F∂b⋅∂b∂a=1×2=2\frac{\partial F}{\partial b} \cdot \frac{\partial b}{\partial a} = 1 \times 2 = 2∂b∂F⋅∂a∂b=1×2=2
- 最终得到：1+2=31 + 2 = 31+2=3（全导数 dFda\frac{dF}{da}dadF）

4.总结

自动微分系统返回的"梯度"本质上是：每个叶节点对目标函数沿计算图所有可达路径的导数之和。

当叶节点到目标函数只有一条路径 时，结果与数学偏导数一致
当叶节点到目标函数有多条路径 时，结果是各路径贡献之和，即数学全导数

这正是深度学习的"潜规则"：理论分析基于数学梯度（偏导数），但实际优化器更新使用的是自动微分计算的导数。在存在参数共享、残差连接等复杂计算图中，这个差异尤为重要。

按需计算机制掩盖了路径依赖关系，使得用户在请求某个变量的梯度时，无法直接区分得到的是偏导数还是全导数，这是理解自动微分与理论分析差异的关键。

事实上，直接理解为全是全导数也可以，因为在某个变量与其他变量不存在依赖的情况下，那么这个变量的全导数和偏导数的表达式和计算值都是相同的，问题不大。

三.总结

1.核心结论

数学梯度 = 独立变量的偏导数向量（假设所有变量独立）
自动微分"梯度" = 叶节点沿计算图所有路径的链式法则导数
- 单路径 → 等于偏导数
- 多路径 → 等于全导数

2.关键差异

理论分析：使用数学梯度（偏导数）
实际训练：使用自动微分计算的导数（可能是全导数）
按需计算：隐藏了路径依赖，用户无法区分得到的是偏导还是全导

3.实用意义

在参数共享、残差连接等复杂网络中，优化器实际更新使用的是全导数而非理论上的偏导数。这是深度学习理论分析与工程实现的重要差异。