2025年11月17日力扣刷题记录。
目录
前言
本文记录了2025年11月17日在力扣刷题的记录,包含数组、字符串和链表题目各一道。
一、数组算法OJ题:最接近的三数之和
我首先把题目链接贴在下面:
题目详细叙述如下:

那么对于这道题,我首先的想法就是首先创建一个长度和输入数组大小相等的数组来存放target减去每个元素的值,然后再弄一个大小为(numsSize - 1) * numsSize / 2的数组,专门把两个元素的加和存放在一起,然后通过遍历来比较这两个数组中元素的接近程度,但是很明显,我们来分析时间复杂度的话,它应该是O(n^3)的级别,所以即使用例通过的话,这也是十分低效的。但是我还是把代码粘过来:
cpp
int threeSumClosest(int* nums, int numsSize, int target) {
// 边界处理:数组长度为3时直接返回三数之和
if (numsSize == 3) {
return nums[0] + nums[1] + nums[2];
}
// 计算sub数组:sub[k] = target - nums[k](用于后续比较两数之和与它的差值)
int* sub = (int*)malloc(sizeof(int) * numsSize);
for (int i = 0; i < numsSize; i++) {
sub[i] = target - nums[i];
}
// 计算所有i<j的两数之和,同时记录对应的i和j索引
int add_length = (numsSize - 1) * numsSize / 2; // 两数之和的总个数
int* add = (int*)malloc(sizeof(int) * add_length); // 存储两数之和
int* i_indices = (int*)malloc(sizeof(int) * add_length); // 存储每个和对应的i
int* j_indices = (int*)malloc(sizeof(int) * add_length); // 存储每个和对应的j
int count = 0;
for (int i = 0; i < numsSize; i++) {
for (int j = i + 1; j < numsSize; j++) {
add[count] = nums[i] + nums[j];
i_indices[count] = i; // 记录当前两数之和的i
j_indices[count] = j; // 记录当前两数之和的j
count++;
}
}
// 初始化:找到第一个有效的三数组合(i、j、k互不相同)
int closestSum = 0;
int minDiff = INT_MAX; // 最小差值,初始化为最大整数
// 遍历add数组,找到第一个能和某个k组成有效三数的组合
for (int m = 0; m < add_length; m++) {
int i = i_indices[m];
int j = j_indices[m];
// 找一个k,既不等于i也不等于j
for (int k = 0; k < numsSize; k++) {
if (k != i && k != j) {
closestSum = add[m] + nums[k]; // 三数之和
minDiff = abs(closestSum - target); // 与target的差值
goto init_done; // 找到后跳出多层循环
}
}
}
init_done:
// 遍历所有可能的三数组合,更新最接近的和
for (int k = 0; k < numsSize; k++) { // 遍历每个可能的第三个数k
for (int m = 0; m < add_length; m++) { // 遍历每个两数之和(i、j)
int i = i_indices[m];
int j = j_indices[m];
// 跳过重复索引:k不能等于i或j(否则三数中有重复元素)
if (k == i || k == j) {
continue;
}
// 计算当前三数之和
int currentSum = add[m] + nums[k];
// 计算与target的差值
int currentDiff = abs(currentSum - target);
// 更新最小差值和最接近的和
if (currentDiff < minDiff) {
minDiff = currentDiff;
closestSum = currentSum;
// 若差值为0,直接返回(不可能更接近了)
if (minDiff == 0) {
// 释放动态内存
free(sub);
free(add);
free(i_indices);
free(j_indices);
return currentSum;
}
}
}
}
// 释放动态内存(避免内存泄漏)
free(sub);
free(add);
free(i_indices);
free(j_indices);
return closestSum;
}
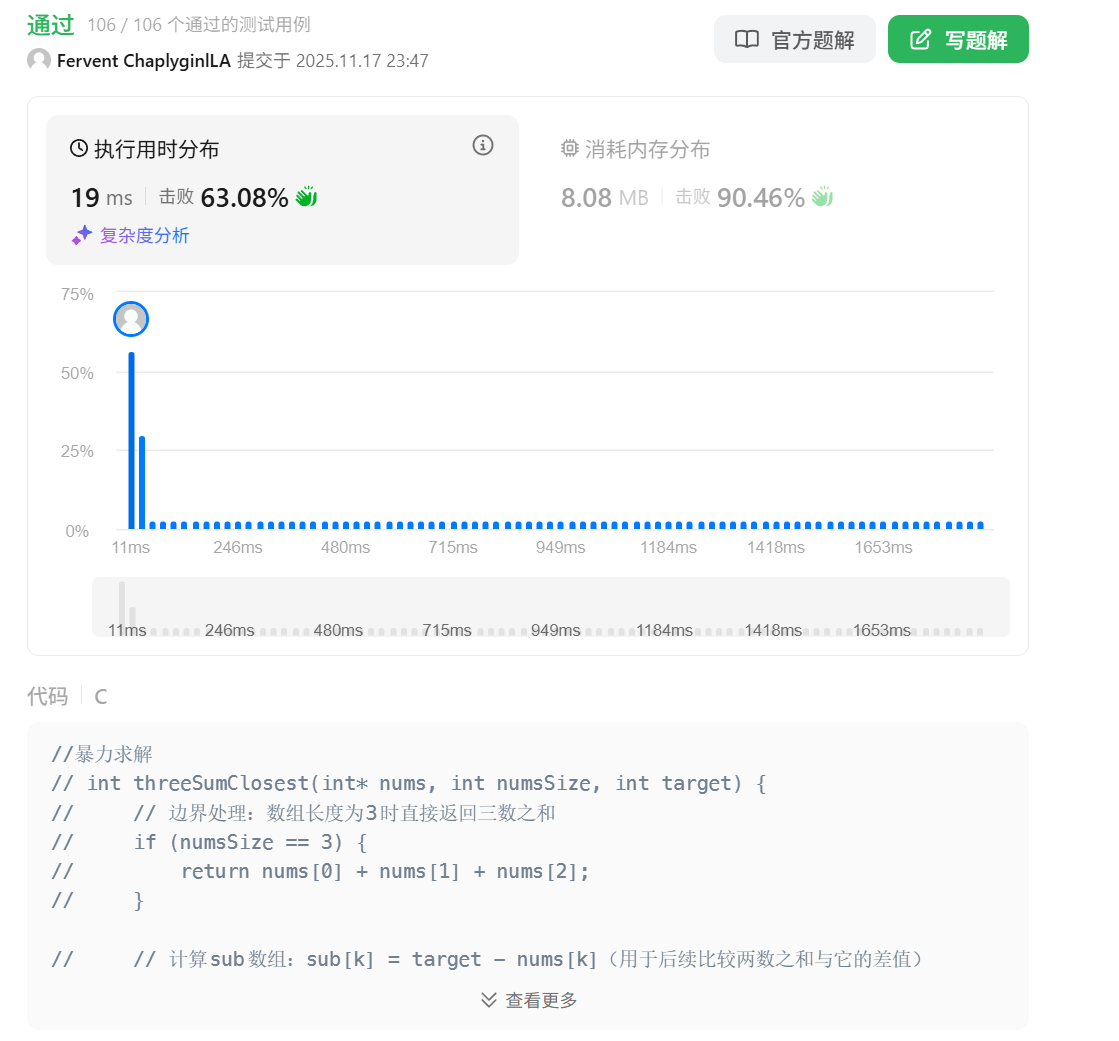
可以看到用例确实通过,但是最后还是超时,所以我参考了下大佬的题解,通过排序和双指针解决问题,因为要计算三个数,如果靠暴力枚举的话时间复杂度会到 O(n^3),需要降低时间复杂度。首先进行数组排序,时间复杂度 O(nlogn),在数组 nums 中,进行遍历,每遍历一个值利用其下标i,形成一个固定值 nums[i];再使用前指针指向 start = i + 1 处,后指针指向end = nums.length - 1处,也就是结尾处;根据 sum = nums[i] + nums[start] + nums[end] 的结果,判断 sum 与目标 target 的距离,如果更近则更新结果 ans;同时判断 sum 与 target 的大小关系,因为数组有序,如果sum > target则end--,如果sum < target则start++,如果 sum == target 则说明距离为 0 直接返回结果整个遍历过程,固定值为 n 次,双指针为 n 次,时间复杂度为 O(n^2)总时间复杂度为O(nlogn)+O(n^2)=O(n^2)。代码如下:
cpp
int compare(const void *a, const void *b) {
return *(int*)a - *(int*)b;
}
int threeSumClosest(int* nums, int numsSize, int target) {
// 对数组进行排序
qsort(nums, numsSize, sizeof(int), compare);
// 初始化答案为前三个元素的和(假设数组长度至少为3,题目通常有此约束)
int ans = nums[0] + nums[1] + nums[2];
for (int i = 0; i < numsSize; i++) {
int start = i + 1; // 左指针从i+1开始
int end = numsSize - 1; // 右指针从数组末尾开始
while (start < end) {
int sum = nums[i] + nums[start] + nums[end];
// 如果当前和更接近目标值,则更新答案
if (abs(target - sum) < abs(target - ans)) {
ans = sum;
}
// 根据和与目标值的大小关系移动指针
if (sum > target) {
end--; // 和太大,右指针左移减小和
} else if (sum < target) {
start++; // 和太小,左指针右移增大和
} else {
// 若和等于目标值,直接返回(已找到最接近的情况)
return ans;
}
}
}
return ans;
}
二、链表算法OJ题:相交链表
我首先把题目链接贴在下面:
题目详细叙述如下:
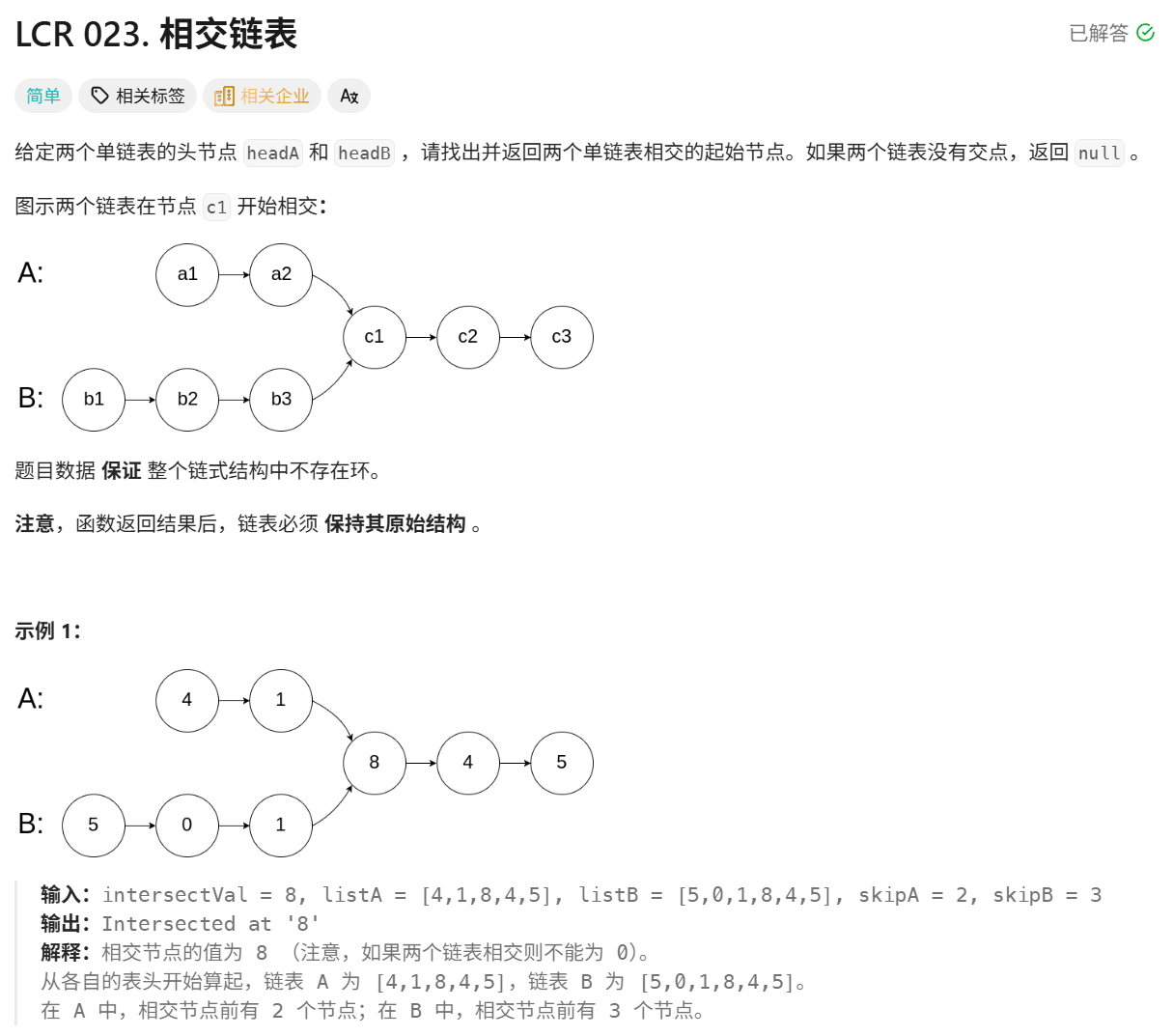
我的思路是这样的,首先判断边界情况,若任一链表为空,直接返回 NULL;然后计算链表长度差,用指针 p1 遍历链表 headA,统计节点数,用指针 p2 遍历链表 headB,统计节点数;接着判断是否可能相交,若两个链表的尾节点不同,说明一定不相交,返回 NULL;而后对齐链表起点,若链表 A 更长,让 p1 先移动 m-n 步,若链表 B 更长,让 p2 先移动 n-m 步,使两指针处于 "剩余长度相同" 的位置;最后同步遍历找交点,同时移动 p1 和 p2,第一个相等的节点即为相交节点,返回该节点。请读者思考代码实现,我这里给出我的代码:
cpp
typedef struct ListNode node;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
if(headA == NULL || headB == NULL){
return NULL;
}
node* p1 = headA;
node* p2 = headB;
int m = 0;
int n = 0;
while(p1->next != NULL){
p1 = p1->next;
m++;
}
while(p2->next != NULL){
p2 = p2->next;
n++;
}
if(p1 != p2){
return NULL;
}
p1 = headA;
p2 = headB;
if(m > n){
int len = m - n;
while(len--){
p1 = p1->next;
}
}else{
int len = n - m;
while(len--){
p2 = p2->next;
}
}
while(p1 != NULL){
if(p1 != p2){
p1 = p1->next;
p2 = p2->next;
}else{
return p1;
}
}
return NULL;
}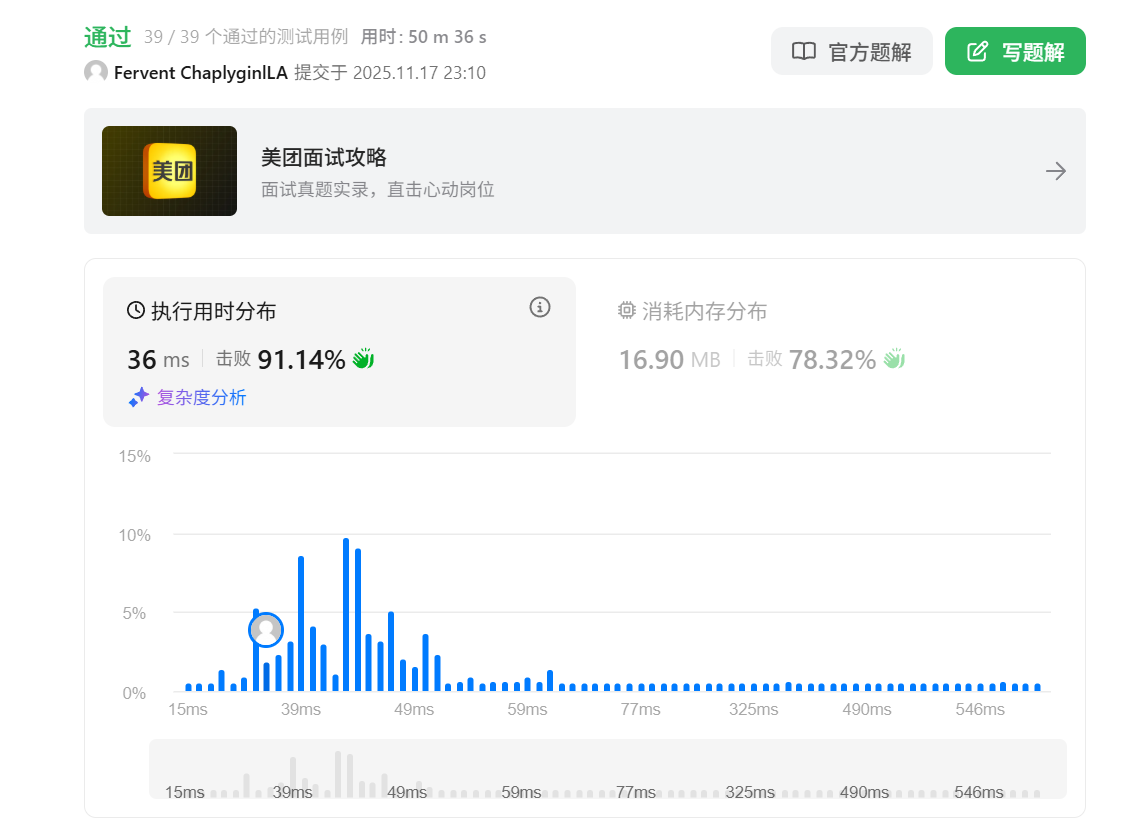
我们这个代码感觉写了很长一段,我就在想是不是可以进行优化,答案显然是可以的。原代码需要先遍历两次计算长度,再遍历两次找交点,共4次遍历。可使用双指针拼接遍历法,只需最多2次遍历,指针 p1 从 headA 出发,到尾后切换到 headB 继续遍历;指针 p2 从 headB 出发,到尾后切换到 headA 继续遍历;若两链表相交,p1 和 p2 会在交点处相遇;若不相交,最终都会指向 NULL。也就是下面的代码:
cpp
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
if (headA == NULL || headB == NULL) {
return NULL;
}
struct ListNode *p1 = headA, *p2 = headB;
// 双指针拼接遍历:若相交则相遇于交点,否则同时到达NULL
while (p1 != p2) {
p1 = (p1 == NULL) ? headB : p1->next; // p1到尾则切换到headB
p2 = (p2 == NULL) ? headA : p2->next; // p2到尾则切换到headA
}
return p1; // 若相交返回交点,否则返回NULL
}
这道题在我们之后学习完哈希表之后,也可以用哈希的方式来解题,这里我们不再赘述。
三、字符串算法OJ题:最后一个单词的长度
我贴出这道题的测试链接:
题目详细叙述如下:

这道题相对来说比较简单,我们可以从字符串末尾倒序遍历,跳过末尾的所有空格,找到最后一个单词的结束位置,然后从结束位置继续倒序,直到遇到空格或字符串开头,统计长度。我给出我的代码:
cpp
int lengthOfLastWord(char* s) {
int len = 0;
int i = 0;
while (s[i] != '\0') {
i++;
}
i--;
while (i >= 0 && s[i] == ' ') {
i--;
}
while (i >= 0 && s[i] != ' ') {
len++;
i--;
}
return len;
}
总结
本文记录了2025年11月17日的力扣刷题情况,包含三道典型算法题。数组题"最接近的三数之和"通过排序+双指针优化,将时间复杂度从O(n^3)降至O(n^2);链表题"相交链表"采用双指针拼接遍历法,在2次遍历内解决问题;字符串题"最后一个单词的长度"通过倒序遍历高效求解。每道题都分析了初始思路和优化方案,展示了算法优化过程。本次刷题涵盖数组、链表、字符串三大基础数据结构,体现了不同数据结构的典型解题方法。