卷积神经网络基础

1. 卷积计算

卷积是数学分析里面的一种积分变换，两个函数的乘积积分得到第三个函数，在图像处理中采用的是卷积的离散形式，在卷积神经网络中，卷积层的实现方式实际上是数学中定义的互相关 （cross-correlation）运算，与数学分析中的卷积定义有所不同

有几个定义先说明一下

1.1 卷积核

卷积核（kernel）也被叫做滤波器（filter），假设卷积核的高和宽分别为khk_hkh​和kwk_wkw​，则将称为kh×kwk_h×k_wkh×kw​卷积，比如3×5卷积，就是指卷积核的高为3, 宽为5。

1.2 计算案例

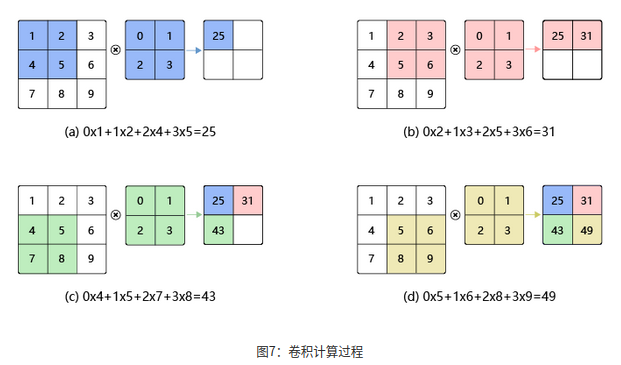
如图7（a）所示：左边的图大小是3×3，表示输入数据是一个维度为3×3的二维数组；中间的图大小是2×2，表示一个维度为2×2的二维数组，我们将这个二维数组称为卷积核。先将卷积核的左上角与输入数据的左上角（即：输入数据的(0, 0)位置）对齐，把卷积核的每个元素跟其位置对应的输入数据中的元素相乘，再把所有乘积相加，得到卷积输出的第一个结果：

0×1+1×2+2×4+3×5=25 (a)

如图7（b）所示：将卷积核向右滑动，让卷积核左上角与输入数据中的(0,1)位置对齐，同样将卷积核的每个元素跟其位置对应的输入数据中的元素相乘，再把这4个乘积相加，得到卷积输出的第二个结果：

0×2+1×3+2×5+3×6=31 (b)

如图7（c）所示：将卷积核向下滑动，让卷积核左上角与输入数据中的(1, 0)位置对齐，可以计算得到卷积输出的第三个结果：

0×4+1×5+2×7+3×8=43 ( c )

如图7（d）所示：将卷积核向右滑动，让卷积核左上角与输入数据中的(1, 1)位置对齐，可以计算得到卷积输出的第四个结果：

0×5+1×6+2×8+3×9=49 (d)

卷积核的计算过程可以用下面的数学公式表示，其中 a 代表输入图片， b 代表输出特征图，w 是卷积核参数，它们都是二维数组，∑u,v 表示对卷积核参数进行遍历并求和。
b[i,j]=∑u,va[i+u,j+v]⋅w[u,v]b[i,j]=\sum\limits_{u,v}a[i+u, j+v] \cdot w[u,v]b[i,j]=u,v∑a[i+u,j+v]⋅w[u,v]

举例说明，假如上图中卷积核大小是2×22\times 22×2，则uuu可以取0和1，vvv也可以取0和1，也就是说：

b[i,j]=a[i+0,j+0]⋅w[0,0]+a[i+0,j+1]⋅w[0,1]+a[i+1,j+0]⋅w[1,0]+a[i+1,j+1]⋅w[1,1]b[i,j]=a[i+0,j+0]⋅w[0,0]+a[i+0,j+1]⋅w[0,1]+a[i+1,j+0]⋅w[1,0]+a[i+1,j+1]⋅w[1,1]b[i,j]=a[i+0,j+0]⋅w[0,0]+a[i+0,j+1]⋅w[0,1]+a[i+1,j+0]⋅w[1,0]+a[i+1,j+1]⋅w[1,1]

读者可以自行验证，当[i,j]取不同值时，根据此公式计算的结果与上图中的例子是否一致。

1.3 偏置项

在卷积神经网络中，一个卷积算子除了上面描述的卷积过程之外，还包括加上偏置项的操作。例如假设偏置为1，则上面卷积计算的结果为：

0×1+1×2+2×4+3×5+1=260×1+1×2+2×4+3×5 +1=260×1+1×2+2×4+3×5+1=26
0×2+1×3+2×5+3×6+1=320×2+1×3+2×5+3×6 +1=320×2+1×3+2×5+3×6+1=32
0×4+1×5+2×7+3×8+1=440×4+1×5+2×7+3×8 +1=440×4+1×5+2×7+3×8+1=44
0×5+1×6+2×8+3×9+1=500×5+1×6+2×8+3×9 +1=500×5+1×6+2×8+3×9+1=50

填充

在上面的例子中，输入图片尺寸为3×33，输出图片尺寸为2×22，经过一次卷积之后，图片尺寸变小。卷积输出特征图的尺寸计算方法如下（卷积核的高和宽分别为khk_hkh​和kwk_wkw​）：
Hout=H−kh+1H_{out}=H−k_h+1Hout=H−kh+1
Wout=W−kw+1W_{out}=W-k_w+1Wout=W−kw+1

如果输入尺寸为4，卷积核大小为3时，输出尺寸为4−3+1=2。读者可以自行检查当输入图片和卷积核为其他尺寸时，上述计算式是否成立。当卷积核尺寸大于1时，输出特征图的尺寸会小于输入图片尺寸。如果经过多次卷积，输出图片尺寸会不断减小。为了避免卷积之后图片尺寸变小，通常会在图片的外围进行填充(padding)，如 图8 所示。

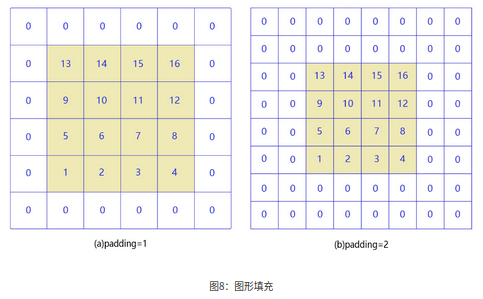
如图8（a）所示：填充的大小为1，填充值为0。填充之后，输入图片尺寸从4×4变成了6×6，使用3×3的卷积核，输出图片尺寸为4×4。

如图8（b）所示：填充的大小为2，填充值为0。填充之后，输入图片尺寸从4×4变成了8×8，使用3×3的卷积核，输出图片尺寸为6×6。

如果在图片高度方向，在第一行之前填充ph1p_{h1}ph1​行，在最后一行之后填充ph2p_{h2}ph2​行；在图片的宽度方向，在第1列之前填充pw1p_{w1}pw1​列，在最后1列之后填充pw2p_{w2}pw2​列；则填充之后的图片尺寸为(H+ph1+ph2)×(W+pw1+pw2)(H+p_{h1}+p_{h2})×(W+p_{w1}+p_{w2})(H+ph1+ph2)×(W+pw1+pw2)。经过大小为kw×khk_w×k_hkw×kh​的卷积核操作之后，输出图片的尺寸为：

Hout=(H+ph1+ph2−kh+1)H_{out} = (H+p_{h1}+p_{h2} - k_h +1)Hout=(H+ph1+ph2−kh+1)
Wout=(W+pw1+pw2−kw+1)W_{out} = (W+p_{w1}+p_{w2} - k_w +1)Wout=(W+pw1+pw2−kw+1)

在卷积计算过程中，通常会在高度或者宽度的两侧采取等量填充，即ph1=ph2=ph, pw1=pw2=pwp_{h1} = p_{h2} = p_h,\ \ p_{w1} = p_{w2} = p_wph1=ph2=ph, pw1=pw2=pw，上面计算公式也就变为：

Hout=H+2ph−kh+1H_{out}=H+2ph−kh+1Hout=H+2ph−kh+1
Wout=W+2pw−kw+1W_{out} = W + 2p_w - k_w + 1Wout=W+2pw−kw+1

卷积核大小通常使用1，3，5，7这样的奇数，如果使用的填充大小为ph=(kh−1)/2，pw=(kw−1)/2p_h=(k_h-1)/2 ，p_w=(k_w-1)/2ph=(kh−1)/2，pw=(kw−1)/2，则卷积之后图像尺寸不变。例如当卷积核大小为3时，padding大小为1，卷积之后图像尺寸不变；同理，如果卷积核大小为5，padding大小为2，也能保持图像尺寸不变。

步幅(stride)

图8 中卷积核每次滑动一个像素点，这是步幅为1的特殊情况。图9 是步幅为2的卷积过程，卷积核在图片上移动时，每次移动大小为2个像素点。

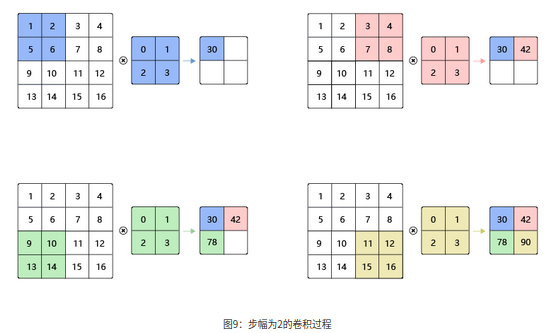
当宽和高方向的步幅分别为shs_hsh​和sws_wsw​时，输出特征图尺寸的计算公式是：

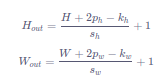
假设输入图片尺寸是H×W=100×100H×W=100×100H×W=100×100，卷积核大小kh×kw=3×3k_h×k_w=3×3kh×kw=3×3，填充ph=pw=1p_h = p_w = 1ph=pw=1，步幅为sh=sw=2s_h = s_w = 2sh=sw=2，则输出特征图的尺寸为：

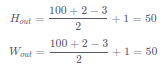
感受野

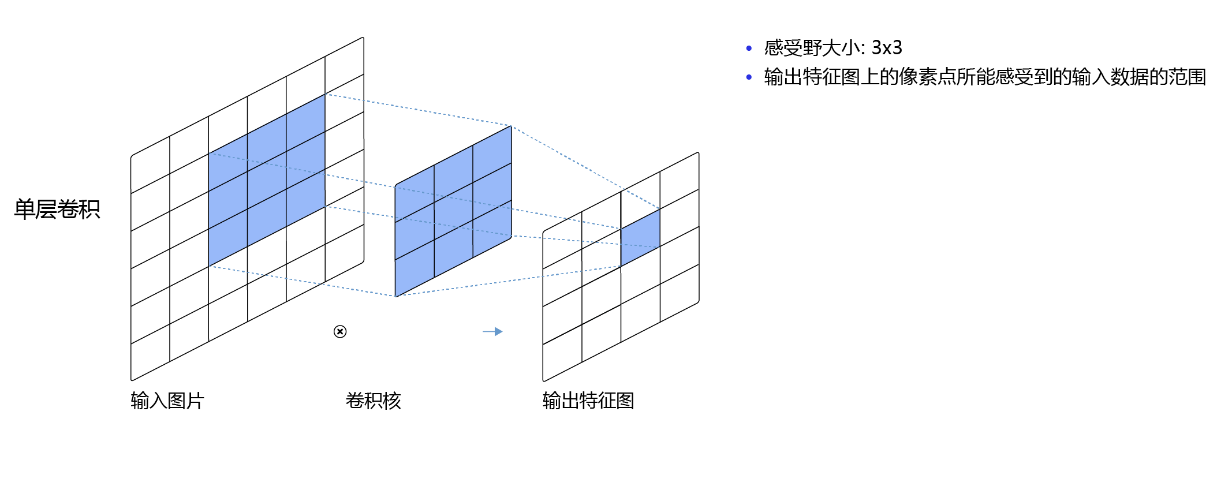
输出特征图上每个点的数值，是由输入图片上大小为kw×khk_w×k_hkw×kh​的区域的元素与卷积核每个元素相乘再相加得到的，所以输入图像上kh×kwk_h×k_wkh×kw区域内每个元素数值的改变，都会影响输出点的像素值。我们将这个区域叫做输出特征图上对应点的感受野。感受野内每个元素数值的变动，都会影响输出点的数值变化。比如3×3卷积对应的感受野大小就是3×3，如 图10 所示。

而当通过两层3×3的卷积之后，感受野的大小将会增加到5×5，如 图11 所示。

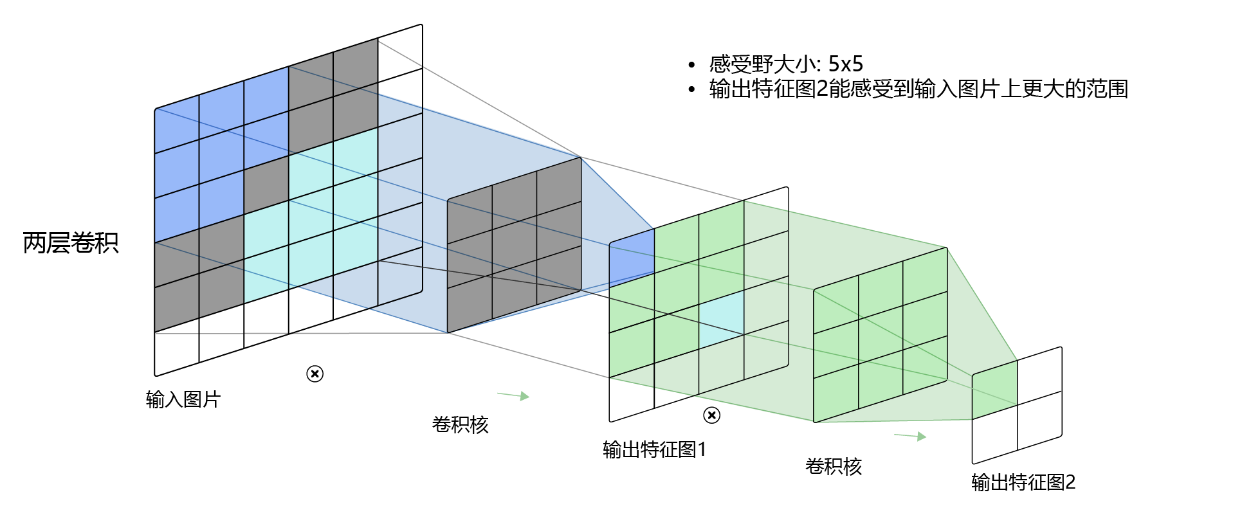
这是因为第二层卷积输出的特征图对应第一层卷积输出的33个点，第一层的每个点又对应原始层的33个点，有部分原始层的点是重合的。因此，当增加卷积网络深度的同时，感受野将会增大，输出特征图中的一个像素点将会包含更多的图像语义信息。

多输入通道、多输出通道和批量操作

前面介绍的卷积计算过程比较简单，实际应用时，处理的问题要复杂的多。例如：对于彩色图片有RGB三个通道，需要处理多输入通道的场景。输出特征图往往也会具有多个通道，而且在神经网络的计算中常常是把一个批次的样本放在一起计算，所以卷积算子需要具有批量处理多输入和多输出通道数据的功能，下面将分别介绍这几种场景的操作方式。

多输入通道场景

上面的例子中，卷积层的数据是一个2维数组，但实际上一张图片往往含有RGB三个通道，要计算卷积的输出结果，卷积核的形式也会发生变化。假设输入图片的通道数为CinC_{in}Cin​，输入数据的形状是Cin×Hin×WinC_{in}×H_{in}×W_{in}Cin×Hin×Win​，计算过程如 图12 所示。

1. 对每个通道分别设计一个2维数组作为卷积核，卷积核数组的形状是Cin×kh×kwC_{in}×k_h×k_wCin×kh×kw​。

2. 对任一通道Cin∈[0,Cin)C_{in}∈[0,C_{in})Cin∈[0,Cin)，分别用大小为kh×kwk_h×k_wkh×kw​的卷积核在大小为Hin×WinH_{in}×W_{in}Hin×Win的二维数组上做卷积。

3. 将这C_{in}​个通道的计算结果相加，得到的是一个形状为Hout×WoutH_{out}×W_{out}Hout×Wout​的二维数组。
   

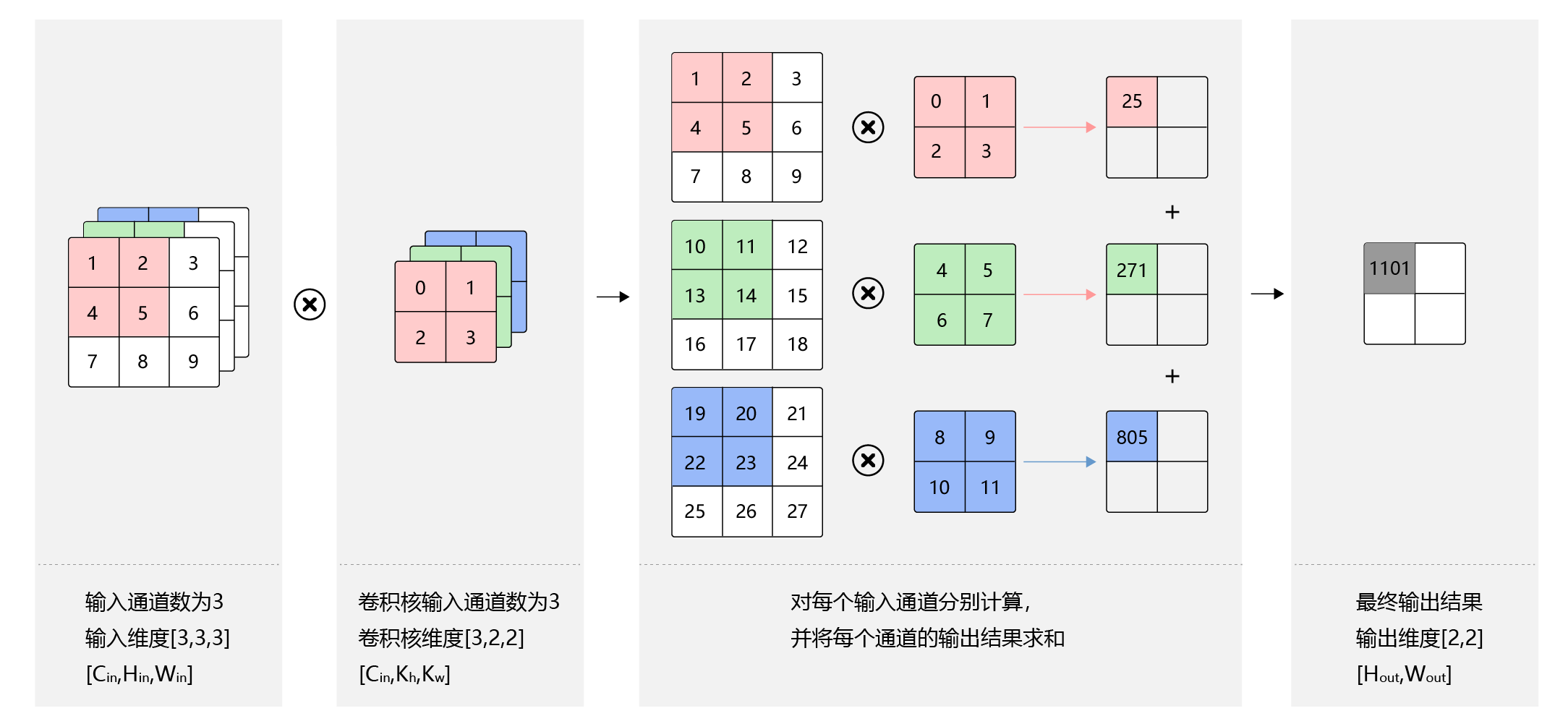
多输出通道场景

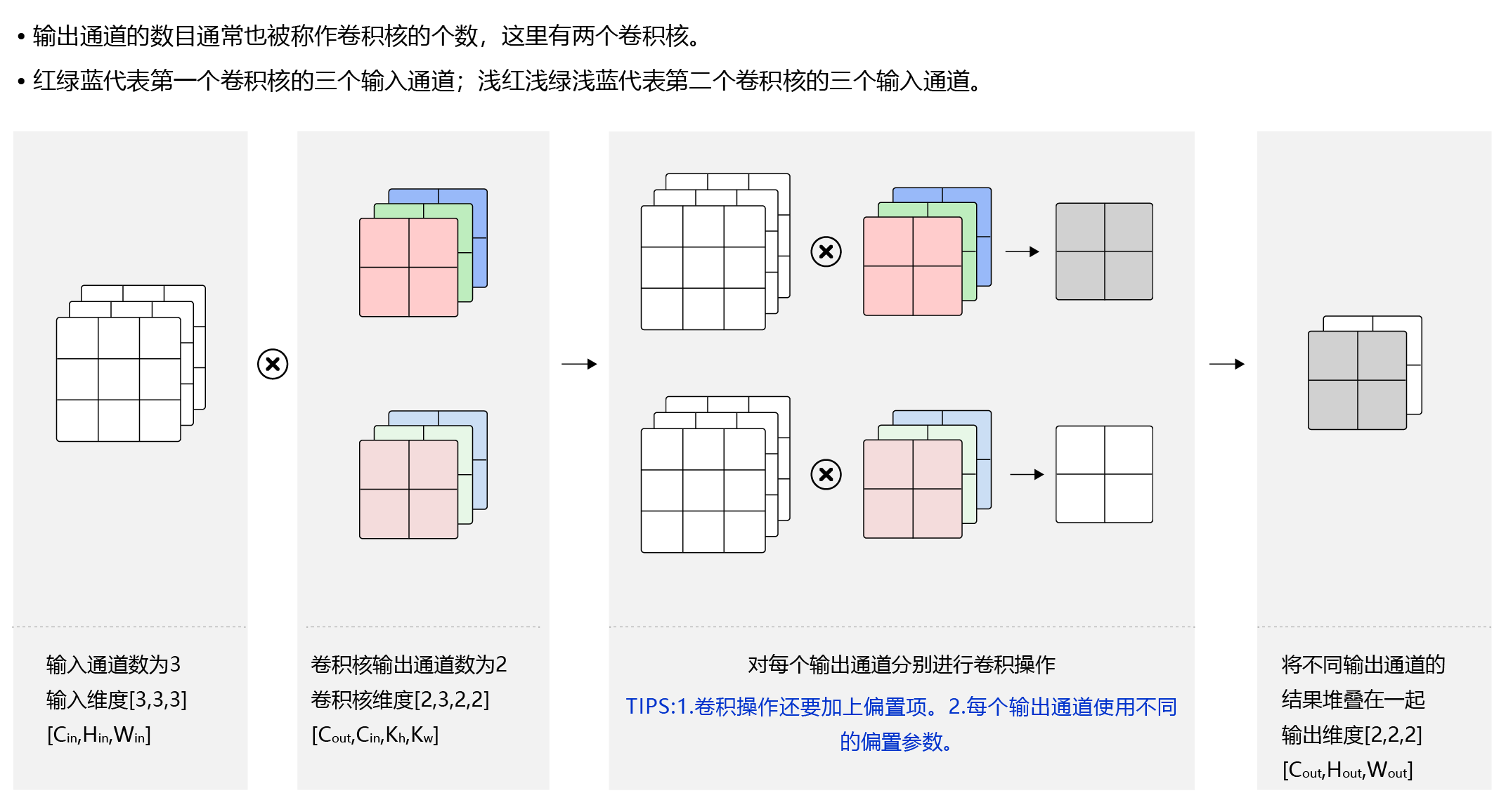
一般来说，卷积操作的输出特征图也会具有多个通道CoutC_{out}Cout​，这时我们需要设计CoutC_{out}Cout​个维度为Cin×kh×kwC_{in}×k_h×k_wCin×kh×kw​的卷积核，卷积核数组的维度是Cout×Cin×kh×kwC_{out}×C_{in}×k_h×k_wCout×Cin×kh×kw​，如 图13 所示。

1. 对任一输出通道cout∈[0,Cout)，分别使用上面描述的形状为Cin×kh×kw的卷积核对输入图片做卷积。
2. 将这Cout个形状为Hout×Wout的二维数组拼接在一起，形成维度为Cout×Hout×Wout的三维数组。

简单力接就是，比单通道的场景多了卷积核，输入分别经过不同的卷积核，得到的结果堆叠起来作为新的特征树组

通常将卷积核的输出通道数叫做卷积核的个数

批量操作

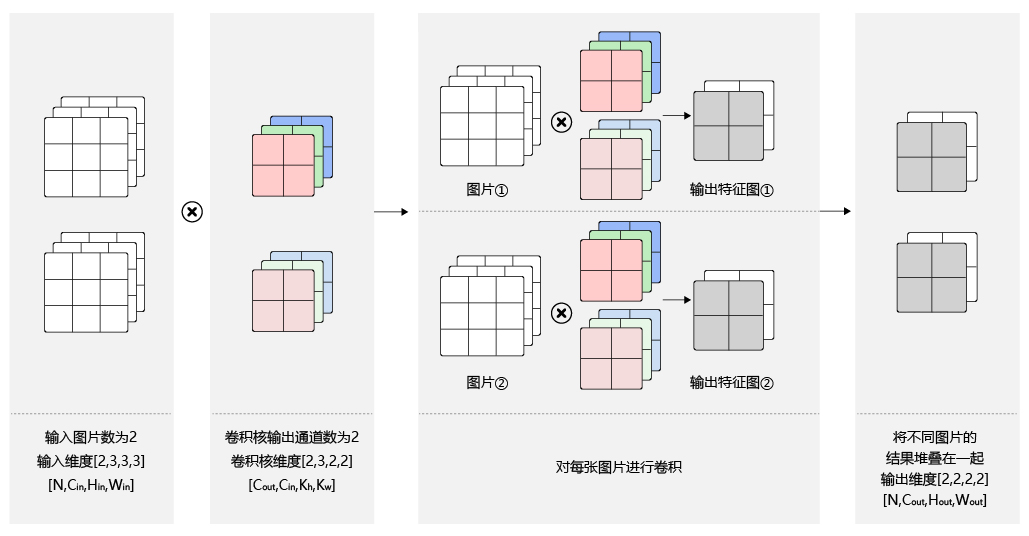
在卷积神经网络的计算中，通常将多个样本放在一起形成一个mini-batch进行批量操作，即输入数据的维度是N×Cin×Hin×Win​。由于会对每张图片使用同样的卷积核进行卷积操作，卷积核的维度与上面多输出通道的情况一样，仍然是Cout×Cin×kh×kw，输出特征图的维度是N×Cout×Hout×Wout，如 图14 所示。

池化(pooling)

池化 通过对输入数据的局部区域进行下采样，减少数据尺寸，同时保留重要特征,其好处是当输入数据做出少量平移时，经过池化函数后的大多数输出还能保持不变。比如：当识别一张图像是否是人脸时，我们需要知道人脸左边有一只眼睛，右边也有一只眼睛，而不需要知道眼睛的精确位置，这时候通过池化某一片区域的像素点来得到总体统计特征会显得很有用。由于池化之后特征图会变得更小，如果后面连接的是全连接层，能有效的减小神经元的个数，节省存储空间并提高计算效率。 如 图15 所示，将一个2×2的区域池化成一个像素点。通常有两种方法，平均池化和最大池化。

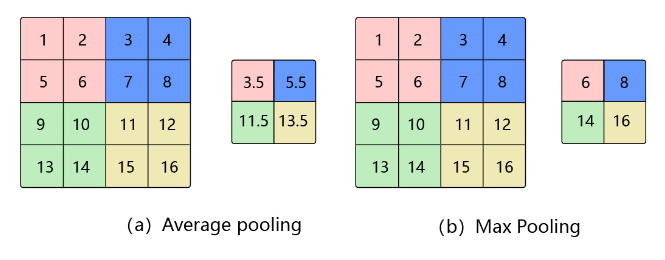
如图15（a）：平均池化。这里使用大小为2×2的池化窗口，每次移动的步幅为2，对池化窗口覆盖区域内的像素取平均值，得到相应的输出特征图的像素值。
如图15（b）：最大池化。对池化窗口覆盖区域内的像素取最大值，得到输出特征图的像素值。当池化窗口在图片上滑动时，会得到整张输出特征图。池化窗口的大小称为池化大小，用kh×kw表示。在卷积神经网络中用的比较多的是窗口大小为2×2，步幅为2的池化。

与卷积核类似，池化窗口在图片上滑动时，每次移动的步长称为步幅，当宽和高方向的移动大小不一样时，分别用sw和sh表示。也可以对需要进行池化的图片进行填充，填充方式与卷积类似，假设在第一行之前填充ph1行，在最后一行后面填充ph2​行。在第一列之前填充pw1列，在最后一列之后填充pw2列，则池化层的输出特征图大小为：

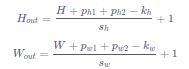
在卷积神经网络中，通常使用2×22大小的池化窗口，步幅也使用2，填充为0，则输出特征图的尺寸为：

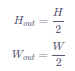
通过这种方式的池化，输出特征图的高和宽都减半，但通道数不会改变。

批归一化（Batch Normalization）

批归一化方法（Batch Normalization，BatchNorm）是由Ioffe和Szegedy于2015年提出的，已被广泛应用在深度学习中，其目的是对神经网络中间层的输出进行标准化处理，使得中间层的输出更加稳定。

通常我们会对神经网络的数据进行标准化处理，处理后的样本数据集满足均值为0，方差为1的统计分布，这是因为当输入数据的分布比较固定时，有利于算法的稳定和收敛。对于深度神经网络来说，由于参数是不断更新的，即使输入数据已经做过标准化处理，但是对于比较靠后的那些层，其接收到的输入仍然是剧烈变化的，通常会导致数值不稳定，模型很难收敛。BatchNorm能够使神经网络中间层的输出变得更加稳定，并有如下三个优点：

使学习快速进行（能够使用较大的学习率）

降低模型对初始值的敏感性

从一定程度上抑制过拟合

BatchNorm主要思路是在训练时以mini-batch为单位，对神经元的数值进行归一化，使数据的分布满足均值为0，方差为1。具体计算过程如下：

1. 计算mini-batch内样本的均值

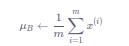
其中x(i)表示mini-batch中的第iii个样本。

例如输入mini-batch包含3个样本，每个样本有2个特征，分别是：

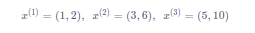
对每个特征分别计算mini-batch内样本的均值：

则样本均值是:

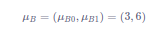
2. 计算mini-batch内样本的方差
   

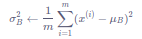
上面的计算公式先计算一个批次内样本的均值μB和方差σB2\sigma_B^2σB2​，然后再对输入数据做归一化，将其调整成均值为0，方差为1的分布。

对于上述给定的输入数据x(1),x(2),x(3)，可以计算出每个特征对应的方差：

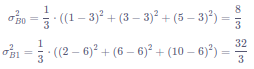
则样本方差是：

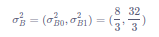
3. 计算标准化之后的输出

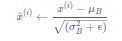
其中ϵ\epsilonϵ是一个微小值（例如1e−7），其主要作用是为了防止分母为0。

对于上述给定的输入数据x(1),x(2),x(3)，可以计算出标准化之后的输出：

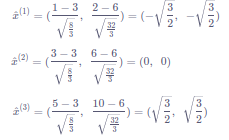
如果强行限制输出层的分布是标准化的，可能会导致某些特征模式的丢失，所以在标准化之后，BatchNorm会紧接着对数据做缩放和平移。

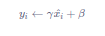
其中γ\gammaγ和β\betaβ是可学习的参数，可以赋初始值γ=1,β=0\gamma = 1, \beta = 0γ=1,β=0，在训练过程中不断学习调整。

上面列出的是BatchNorm方法的计算逻辑，下面针对两种类型的输入数据格式分别进行举例。飞桨支持输入数据的维度大小为2、3、4、5四种情况，这里给出的是维度大小为2和4的示例。

示例一： 当输入数据形状是[N,K]时，一般对应全连接层的输出，示例代码如下所示。

这种情况下会分别对K的每一个分量计算N个样本的均值和方差，数据和参数对应如下：

1. 输入 x, [N, K]
2. 输出 y, [N, K]
3. 均值 μB,[K, ]
4. 方差σB2\sigma_B^2σB2, [K, ]
5. 缩放参数γ\gammaγ, [K, ]
6. 平移参数β, [K, ]