LeetCode 11. 盛最多水的容器

目录

• 原题
• 题目解析
• 算法原理
• 代码实现

原题

盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线 ，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明： 你不能倾斜容器。

示例 1 ：

输入：[1,8,6,2,5,4,8,3,7]

输出：49

示例 2 ：

输入：height = [1,1]

输出：1

题目解析

本题要想清楚题目的要求，就需要对题目给出的示例和图片进行分析了：

示例 1：

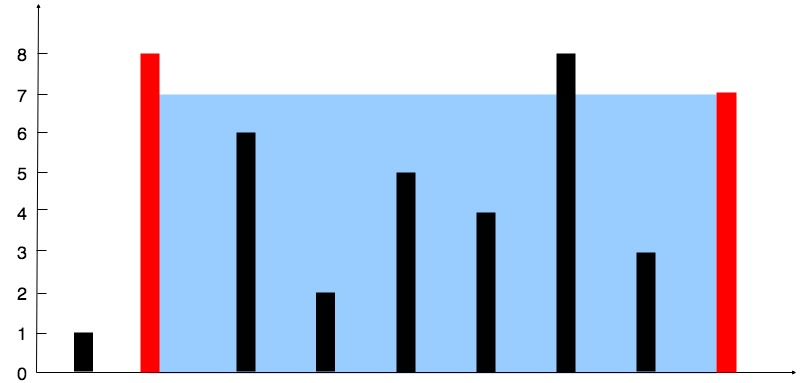
在示例 1 中，height数组中有 9 个值，对应着图片中 9 条垂线每一条的高度，选出其中的两条垂线，然后用这两条垂线组成一个容器并计算它的容量，我们要做的就是选出容器的最大容量并返回

算法原理

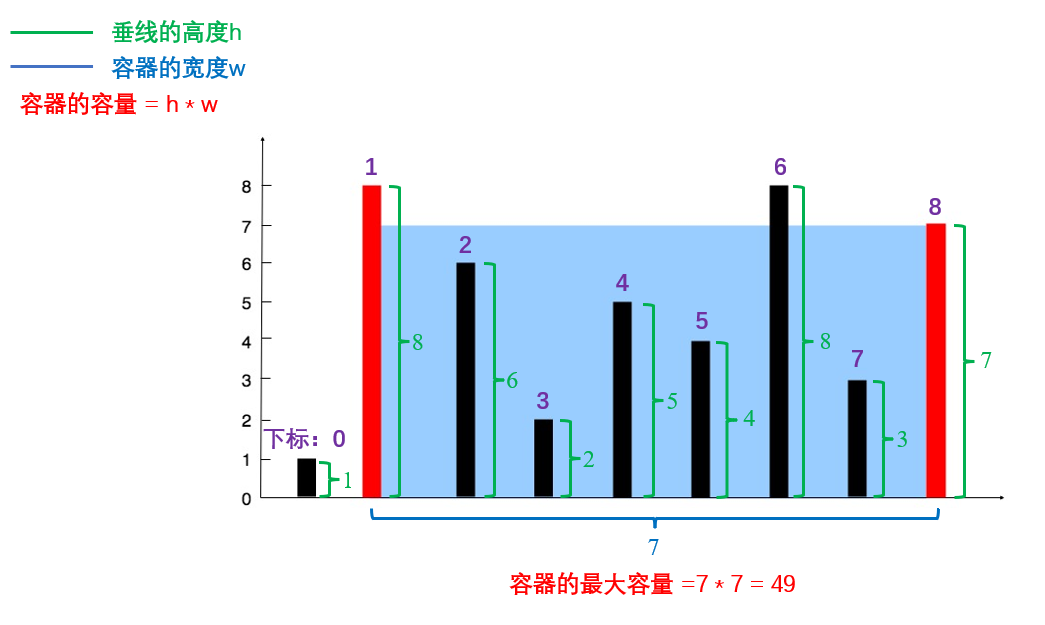
根据示例 1 给出的图片可知，两条垂线组成一个容器时，容器的高度 h 取最短的那一条，容器的宽度 w 取两条垂线对应的下标的差，容器的容量 v = 容器的高度 h * 容器的宽度 w

对于这道题，是存在单调性的，如果我们在左右端点设置两个指针，并让两个指针向中间移动时，我们会发现，宽度是一直在减少的，但是高度可能增加，可能减少，也可能不变。根据容量的式子，我们可以知道：

• 容器的高度 h 减少，容器的宽度 w 减少时，容器的容量 v 也会减少
• 容器的高度 h 不变，容器的宽度 w 减少时，容器的容量 v 也会减少
• 容器的高度 h 增加，容器的宽度 w 减少时，容器的容量 v 可能增加，也可能减少

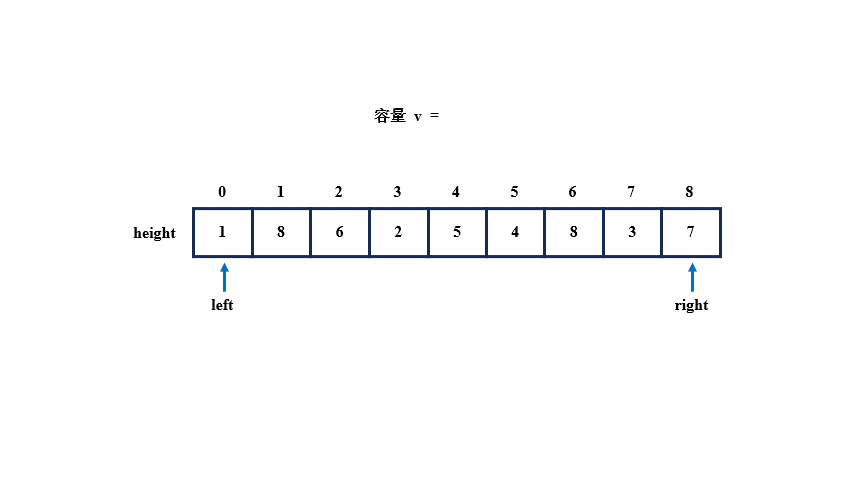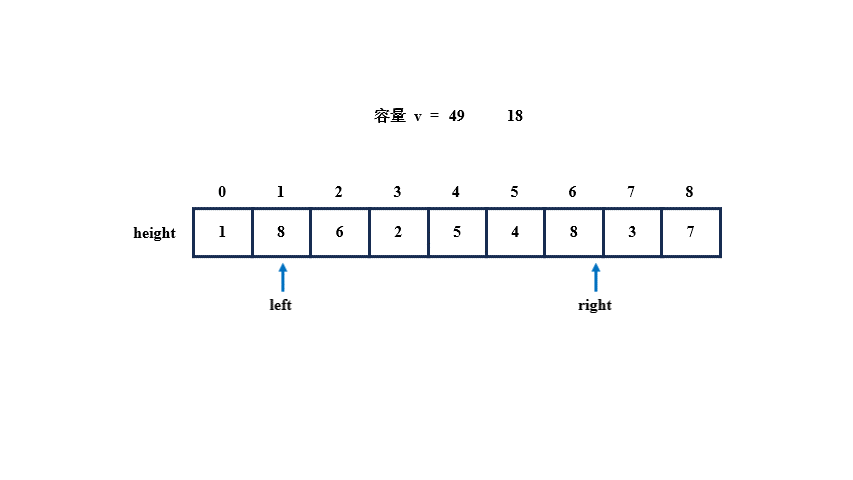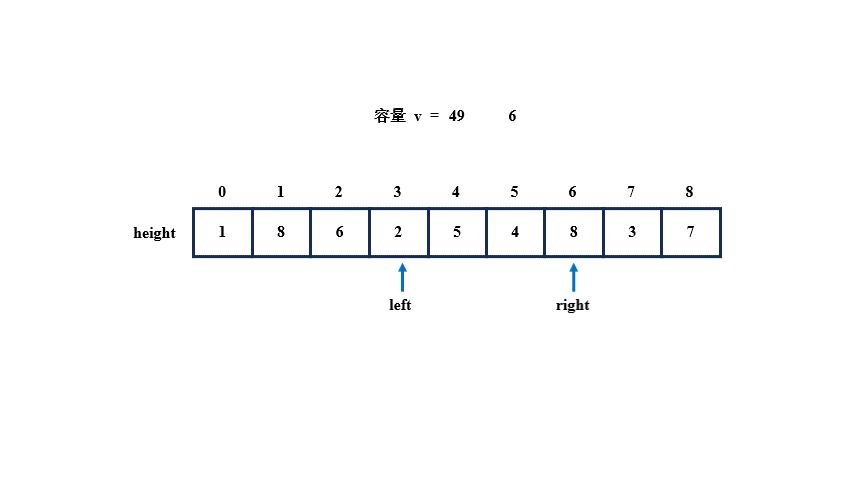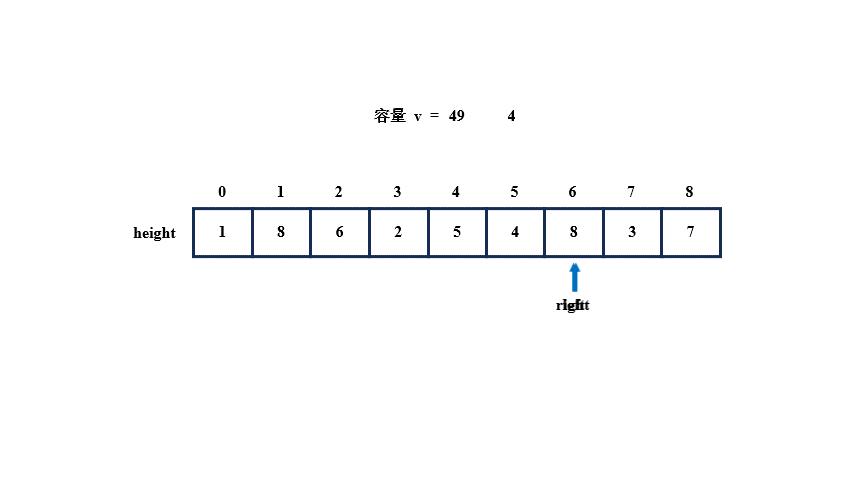
所以，我们可以设置两个指针 left 和 right，让 left 指向最左侧的数，让 right 指向最右侧的数，先通过 left 和 right 指向的两个数中的最小数（高度）以及下标之差（宽度）计算出一个容量保存起来，再比较 left 和 right 指向的值，若 left 指向的更小，left++，否则 right--，如果指向的值相同，则移动哪个都可以，因为小值的后方或前方可能有更大的值，所以让较小的移动，寻找更大的高度并继续计算容量，当容量比之前的大就进行更新，直到 left 与 right 相遇为止，就算出了最大容量

代码实现

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0;
        int right = height.size() - 1;
        int capacity = 0;

        while (left != right)
        {
            //取最短的木板
            int minHeight = height[left] <= height[right] ?  height[left] : height[right];
            //当前的容量更大，更新容量
            if (minHeight * (right - left) > capacity)
            {
                capacity = minHeight * (right - left);
            }

            //排除小的值
            if (height[left] <= height[right])
            {
                left++;
            }
            else
            {
                right--;
            }
        }

        return capacity;
    }
};