算法奇妙屋(二十三)-完全背包问题(动态规划)

文章目录

[一. 牛客 [DP42 【模板】完全背包](https://www.nowcoder.com/practice/237ae40ea1e84d8980c1d5666d1c53bc?tpId=230\&tqId=38965\&ru=/exam/oj)](#一. 牛客 DP42 【模板】完全背包)
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- - [(1) 第一问](#(1) 第一问)
  - [(2) 第二问](#(2) 第二问)
- [3. 代码](#3. 代码)
- [4. 优化](#4. 优化)
- [5. 优化后的代码](#5. 优化后的代码)
[二. 力扣 [322. 零钱兑换](https://leetcode.cn/problems/coin-change/description/)](#二. 力扣 322. 零钱兑换)
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [4. 优化后的代码](#4. 优化后的代码)
[三. 力扣 [518. 零钱兑换 II](https://leetcode.cn/problems/coin-change-ii/description/)](#三. 力扣 518. 零钱兑换 II)
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [4. 优化后的代码](#4. 优化后的代码)
[四. 力扣 [279. 完全平方数](https://leetcode.cn/problems/perfect-squares/description/)](#四. 力扣 279. 完全平方数)
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [4. 优化后的代码](#4. 优化后的代码)

一. 牛客 DP42 【模板】完全背包

1. 题目解析

和01背包很相似, 却又有些许不同

2. 算法原理

(1) 第一问

(2) 第二问

3. 代码

java 复制代码

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    static Scanner in = new Scanner(System.in);
    static int n = in.nextInt();
    static int V = in.nextInt();
    public static void main(String[] args) {
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextInt()) { // 注意 while 处理多个 case
            int[] v = new int[n + 1];
            int[] w = new int[n + 1];
            for (int i = 1; i <= n; i++) {
                v[i] = in.nextInt();
                w[i] = in.nextInt();
            }
            f1(v, w);
            f2(v, w);
        }
    }
    static void f1(int[] v, int[] w) {
        // 建表
        int[][] dp = new int[n + 1][V + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= V; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j >= v[i]) {
                    dp[i][j] = Math.max(dp[i][j], dp[i][j - v[i]] + w[i]);
                }
            }
        }
        System.out.println(dp[n][V]);
    }
    static void f2(int[] v, int[] w) {
        // 建表
        int[][] dp = new int[n + 1][V + 1];
        // 初始化
        for (int j = 1; j <= V; j++) {
            dp[0][j] = -1;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= V; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j >= v[i] && dp[i][j - v[i]] != -1) {
                    dp[i][j] = Math.max(dp[i][j], dp[i][j - v[i]] + w[i]);
                }
            }
        }
        System.out.println(dp[n][V] == -1 ? 0 : dp[n][V]);
    }
}

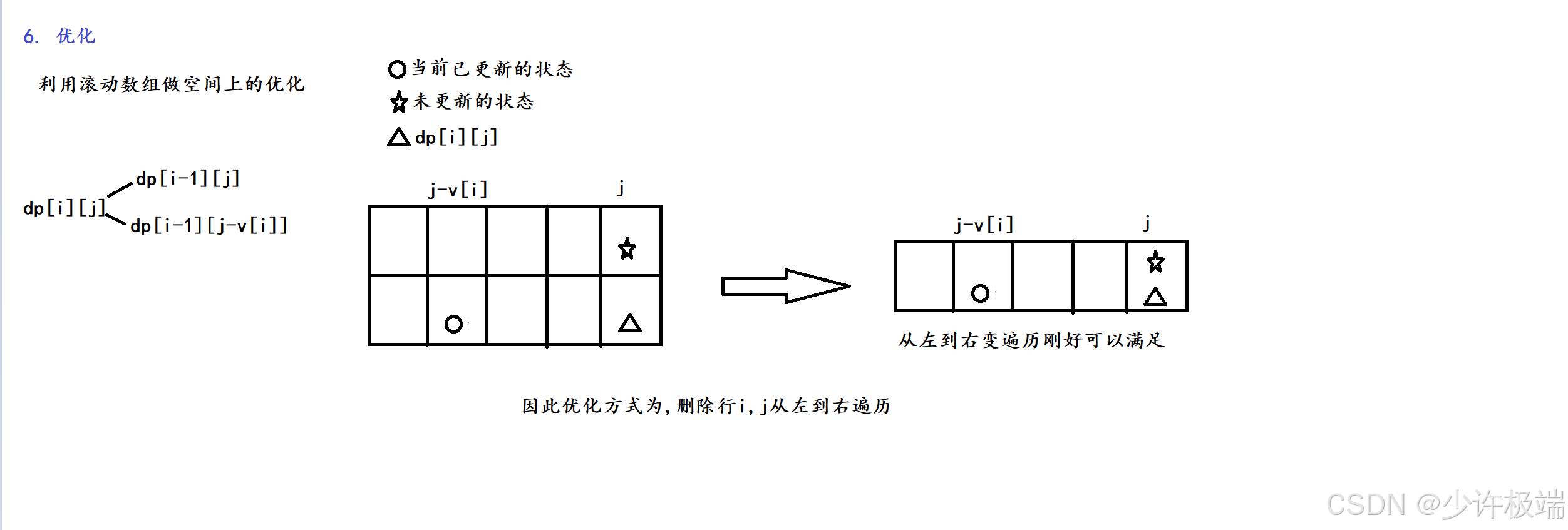
4. 优化

优化过程和01背包一样, 也是利用滚动数组进行空间上的优化

5. 优化后的代码

java 复制代码

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    static Scanner in = new Scanner(System.in);
    static int n = in.nextInt();
    static int V = in.nextInt();
    public static void main(String[] args) {
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextInt()) { // 注意 while 处理多个 case
            int[] v = new int[n + 1];
            int[] w = new int[n + 1];
            for (int i = 1; i <= n; i++) {
                v[i] = in.nextInt();
                w[i] = in.nextInt();
            }
            f1(v, w);
            f2(v, w);
        }
    }
    static void f1(int[] v, int[] w) {
        // 建表
        int[] dp = new int[V + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = v[i]; j <= V; j++) {
                dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
            }
        }
        System.out.println(dp[V]);
    }
    static void f2(int[] v, int[] w) {
        // 建表
        int[] dp = new int[V + 1];
        // 初始化
        for (int j = 1; j <= V; j++) {
            dp[j] = -1;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = v[i]; j <= V; j++) {
                if (dp[j - v[i]] != -1) {
                    dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
                }
            }
        }
        System.out.println(dp[V] == -1 ? 0 : dp[V]);
    }
}

二. 力扣 322. 零钱兑换

1. 题目解析

当我们看到一个元素可以选任意多个时, 要试着转化为完全背包问题

2. 算法原理

要注意区别理解这里为什么不能用-1来代表数值和不能等于j的情况

3. 代码

java 复制代码

class Solution {
    public int coinChange(int[] coins, int amount) {
        // 建表
        int n = coins.length;
        int[][] dp = new int[n + 1][amount + 1];
        // 初始化
        for (int j = 1; j <= amount; j++) {
            dp[0][j] = 0x3f3f3f3f;
        }
        // 填表
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= amount; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j >= coins[i - 1]) {
                    dp[i][j] = Math.min(dp[i][j], dp[i][j - coins[i - 1]] + 1);
                }
            }
        }
        // 返回结果
        return dp[n][amount] >= 0x3f3f3f3f ? -1 : dp[n][amount];
    }
}

4. 优化后的代码

删除 i 维度, j 的范围缩小, 优化的算法原理推导过程在第一题

java 复制代码

class Solution {
    public int coinChange(int[] coins, int amount) {
        // 建表
        int n = coins.length;
        int[] dp = new int[amount + 1];
        // 初始化
        for (int j = 1; j <= amount; j++) {
            dp[j] = 0x3f3f3f3f;
        }
        // 填表
        for (int i = 1; i <= n; i++) {
            for (int j = coins[i - 1]; j <= amount; j++) {
                dp[j] = Math.min(dp[j], dp[j - coins[i - 1]] + 1);
            }
        }
        // 返回结果
        return dp[amount] >= 0x3f3f3f3f ? -1 : dp[amount];
    }
}

三. 力扣 518. 零钱兑换 II

1. 题目解析

这道题和上一道题基本类似, 只是细节稍有不同

2. 算法原理

这里我们省略了选择i号硬币时的推导过程

3. 代码

java 复制代码

class Solution {
    public int change(int amount, int[] coins) {
        //建表
        int n = coins.length;
        int[][] dp = new int[n + 1][amount + 1];
        //初始化
        dp[0][0] = 1;
        //填表
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= amount; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j >= coins[i - 1]) {
                    dp[i][j] = dp[i][j] + dp[i][j - coins[i - 1]];
                }
            }
        }
        //返回结果
        return dp[n][amount];
    }
}

4. 优化后的代码

删除 i 维度, j 的范围缩小, 优化的算法原理推导过程在第一题

java 复制代码

class Solution {
    public int change(int amount, int[] coins) {
        //建表
        int n = coins.length;
        int[] dp = new int[amount + 1];
        //初始化
        dp[0] = 1;
        //填表
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= amount; j++) {
                dp[j] = dp[j];
                if (j >= coins[i - 1]) {
                    dp[j] += dp[j - coins[i - 1]];
                }
            }
        }
        //返回结果
        return dp[amount];
    }
}

四. 力扣 279. 完全平方数

1. 题目解析

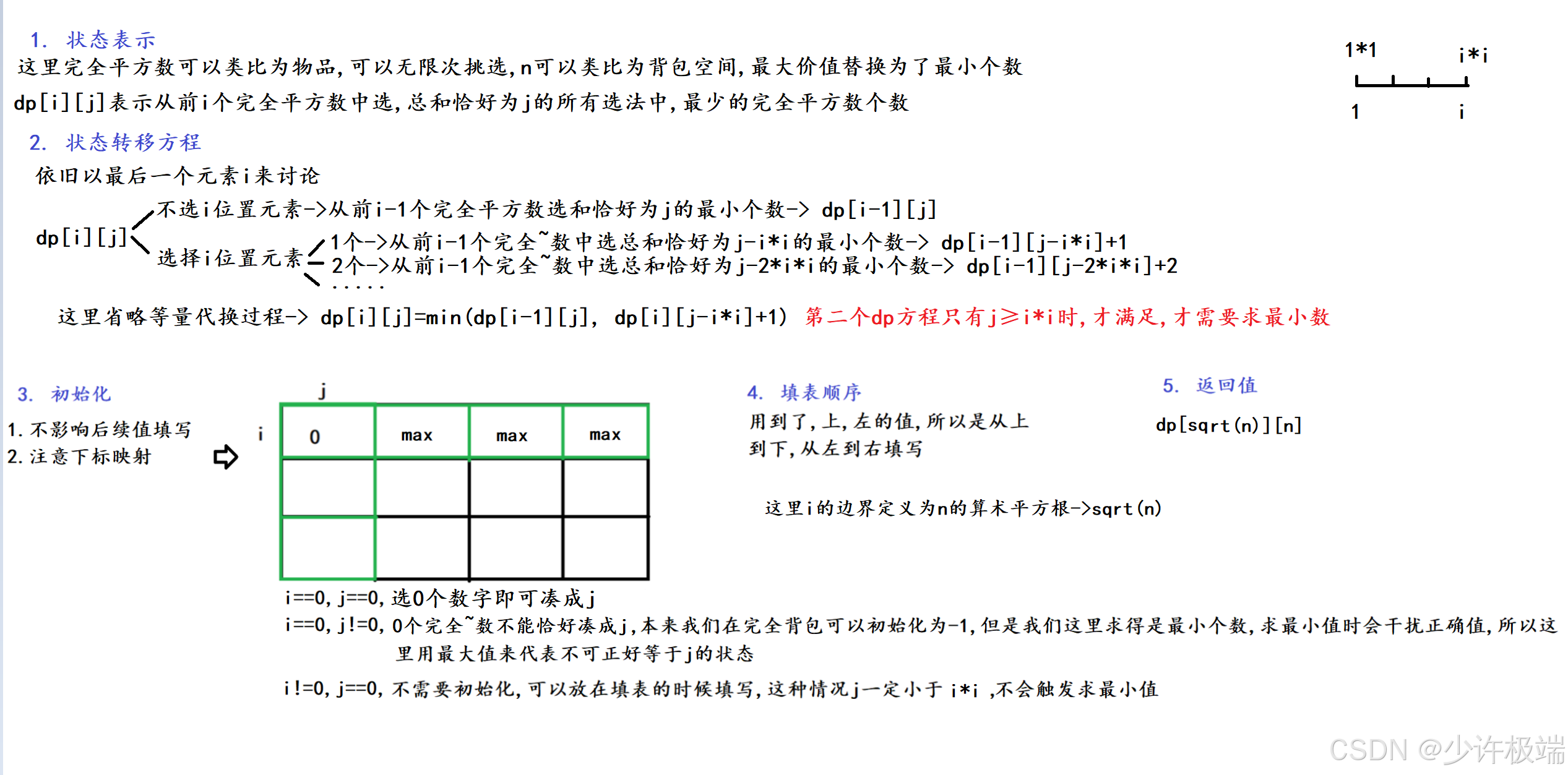
2. 算法原理

完全背包原理相信大家已经掌握, 这里只简单点一下细节方面

3. 代码

java 复制代码

class Solution {
    public int numSquares(int n) {
        // 建表
        int sn = (int)Math.sqrt(n);
        int[][] dp = new int[sn + 1][n + 1];
        // 初始化
        for (int j = 1; j <= n; j++) {
            dp[0][j] = 0x3f3f3f3f;
        }
        // 填表
        for (int i = 1; i <= sn; i++) {
            for (int j = 0; j <= n; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j >= i * i) {
                    dp[i][j] = Math.min(dp[i][j], dp[i][j - i * i] + 1);
                }
            }
        }
        // 返回结果
        return dp[sn][n];
    }
}

4. 优化后的代码

删除 i 维度, j 的范围缩小, 优化的算法原理推导过程在第一题

java 复制代码

class Solution {
    public int numSquares(int n) {
        // 建表
        int sn = (int) Math.sqrt(n);
        int[] dp = new int[n + 1];
        // 初始化
        for (int j = 1; j <= n; j++) {
            dp[j] = 0x3f3f3f3f;
        }
        // 填表
        for (int i = 1; i <= sn; i++) {
            for (int j = i * i; j <= n; j++) {
                dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
            }
        }
        // 返回结果
        return dp[n];
    }
}