OpenGL的3D编程个人笔记之材质贴图

前言

笔记灵感来源：C++和OpenGL实现3D游戏编程【连载5】------纹理坐标、纹理贴图（附源码）
_{支持原作者↑}

四边形材质贴图

菱形

c 复制代码

// 启用二维纹理，调用特定编号的纹理
glEnable(GL_TEXTURE_2D);
// 绑定纹理
glBindTexture(GL_TEXTURE_2D, texture);
// 按照三角形截取，开始
glBegin(GL_QUADS);
// 菱形点(0.5, 0)
glTexCoord2f(0.5f, 0.0f);
// 图形的三维坐标
glVertex3f(0.5f, 0.0f, 0.0f);

// 菱形点(1.0, 0.5)
glTexCoord2f(1.0f，0.5f);
glVertex3f(1.0f, 0.5f, 0.0f);

// 菱形点(0.5, 0.5)
glTexCoord2f(0.5f, 0.5f);
glVertex3f(0.5f, 0.5f, 0.0f);

// 菱形点(0.0, 0.5)
glTexCoord2f(0.0f，0.5f);
glVertex3f(0.0f, 0.5f, 0.0f);
// 结束
glEnd();
// 关闭纹理贴图
glDisable(GL_TEXTURE_2D);

平行四边形

梯形

直角梯形和等腰梯形

三角形材质贴图

直角三角形

3 0 ∘ 30^\circ 30∘直角三角形和 4 5 ∘ 45^\circ 45∘等腰直角三角形

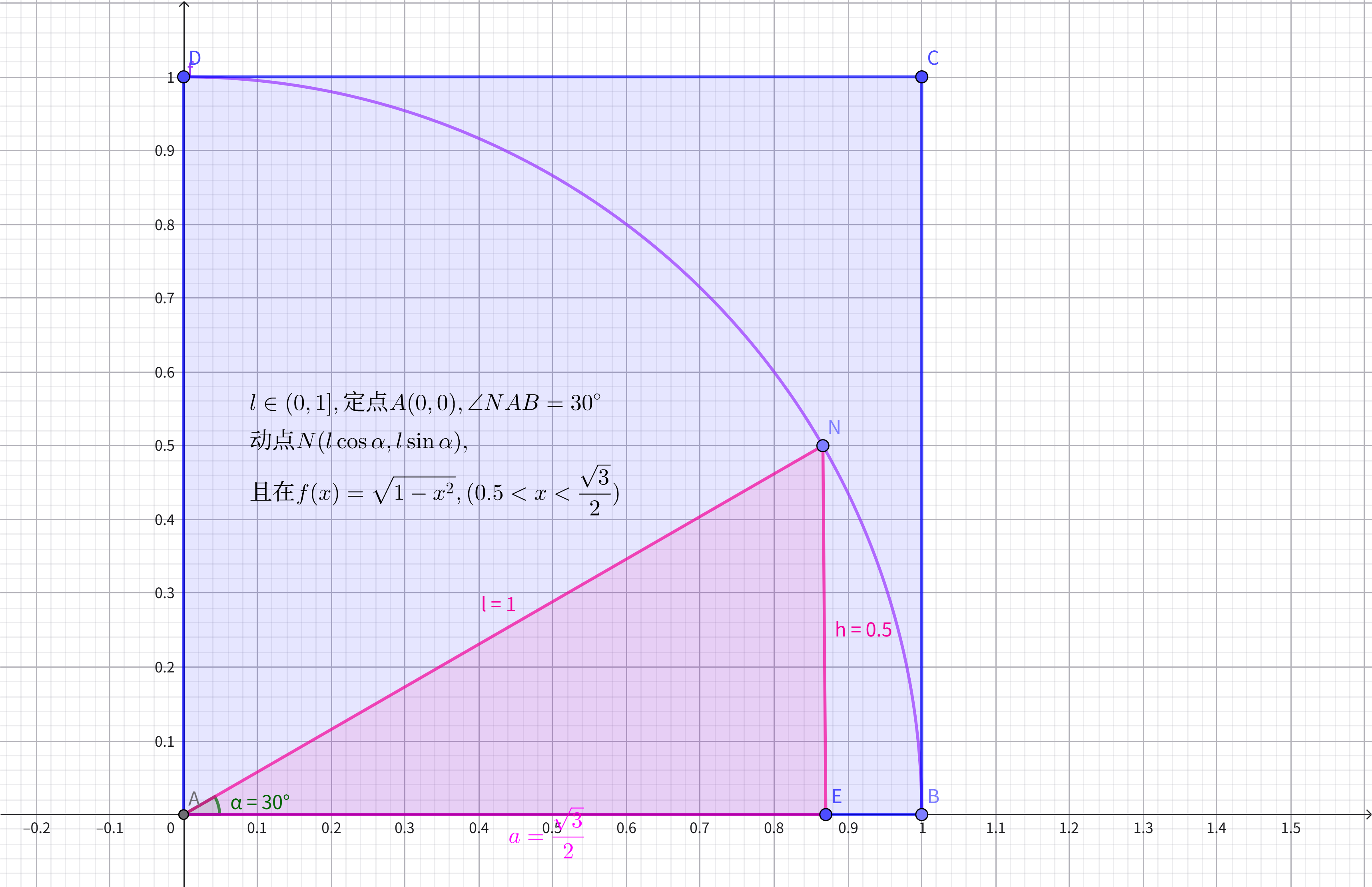
c 复制代码

// 启用二维纹理，调用特定编号的纹理
glEnable(GL_TEXTURE_2D);
// 绑定纹理
glBindTexture(GL_TEXTURE_2D, texture);
// 按照三角形截取，开始
glBegin(GL_TRIANGLE_STRIP);
// 定点A(0, 0)
glTexCoord2f(0.0f, 0.0f);
// 图形的三维坐标
glVertex3f(0.0f, 0.0f, 0.0f);
// 边长l这里是动态的
float l = 1.0; // (0 < l < 1)
// 动点横坐标x_N
double x = l*cos(30.0);
// 动点纵坐标y_N
double y = l*sin(30.0);
// 定点A(0, 0)
glTexCoord2f(0.0f，0.0f);
glVertex3f(0.0f, 0.0f, 0.0f);
// 动点N(x, y)
glTexCoord2f(x，y);
glVertex3f(sqrt(3), 1.0f, 0.0f);
// N点垂直点E(l*cos(30), 0)
glTexCoord2f(x，0.0f);
glVertex3f(sqrt(3), 0.0f, 0.0f);
// 结束
glEnd();
// 关闭纹理贴图
glDisable(GL_TEXTURE_2D);

边长为 3 , 4 , 5 3, 4, 5 3,4,5直角三角形

边长为 5 , 12 , 13 , 5, 12, 13, 5,12,13,直角三角形

6 0 ∘ 60^\circ 60∘等边三角形

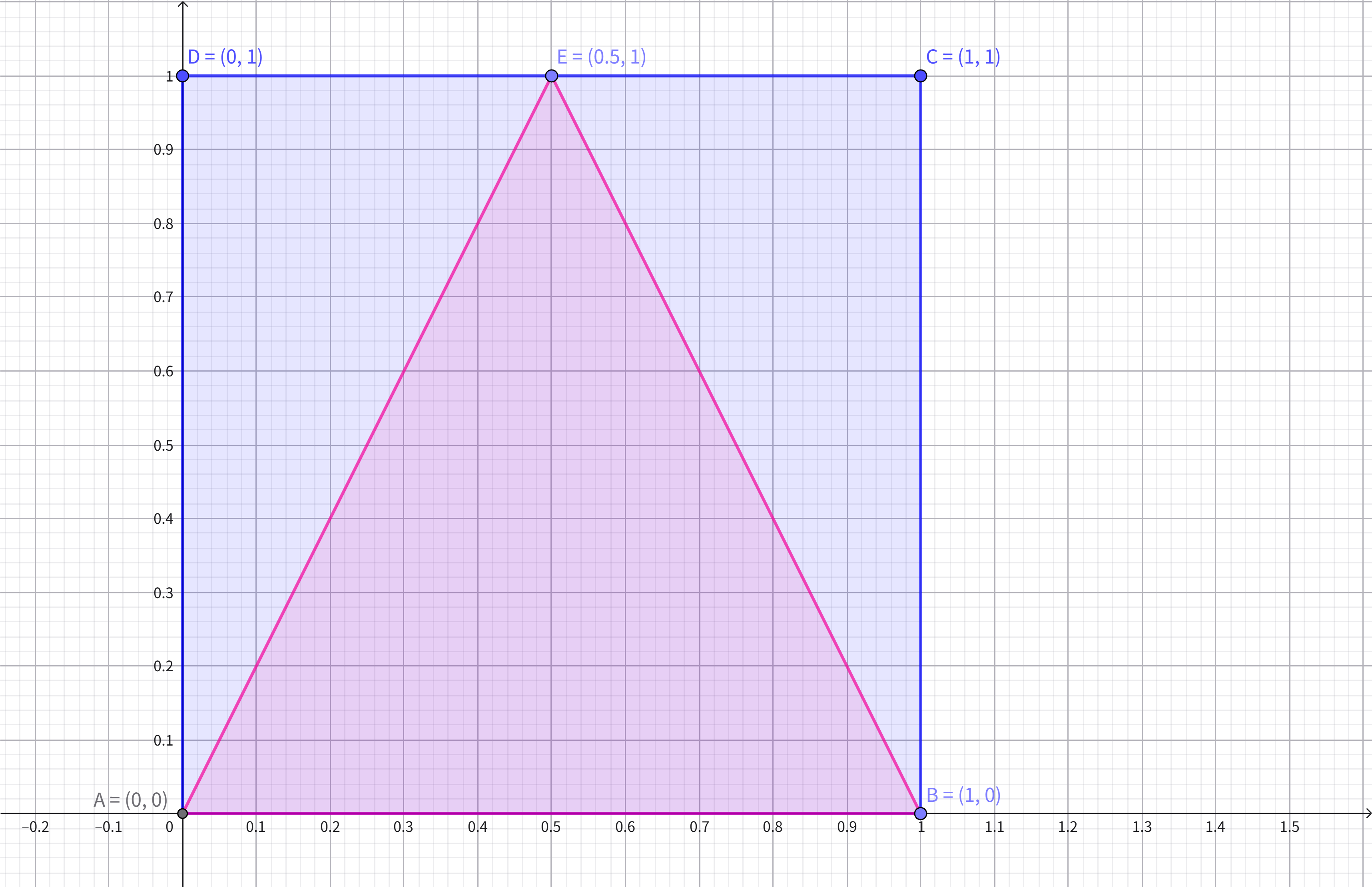
c 复制代码

// 启用二维纹理，调用特定编号的纹理
glEnable(GL_TEXTURE_2D);
// 绑定纹理
glBindTexture(GL_TEXTURE_2D, texture);
// 按照三角形截取，开始
glBegin(GL_TRIANGLE_STRIP);
// 定点A(0, 0)
glTexCoord2f(0.0f, 0.0f);
// 图形的三维坐标
glVertex3f(0.0f, 0.0f, 0.0f);

// C点和D点的中点E(0.5, 0)
glTexCoord2f(0.5f，0.0f);
glVertex3f(0.5f, 0.0f, 0.0f);

// A点(0, 0)
glTexCoord2f(0.0f, 0.0f);
glVertex3f(0.0f, 0.0f, 0.0f);

// B点(1, 0)
glTexCoord2f(1.0f，0.0f);
glVertex3f(1.0f, 0.0f, 0.0f);
// 结束
glEnd();
// 关闭纹理贴图
glDisable(GL_TEXTURE_2D);

五角星材质贴图

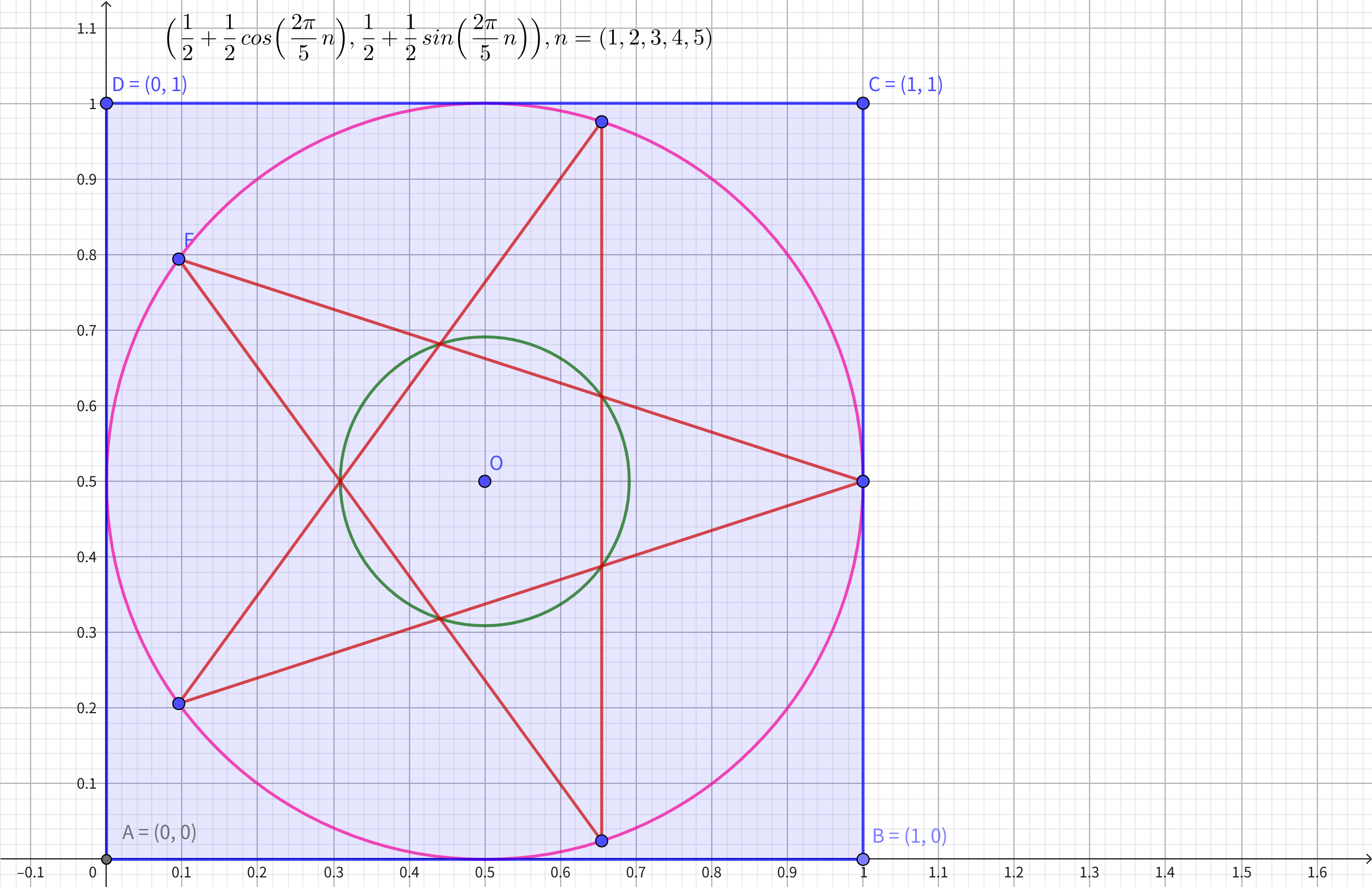
圆形材质贴图

可以是多边形材质贴图：三十六边形

首先获取纹理

c 复制代码

glBindTexture(GL_TEXTURE_2D, texture);

其次用三角形状Triangle Strip进行截取

c 复制代码

glBegin(GL_TRIANGLE_STRIP);

获取纹理中心位置 ( 0.5 , 0.5 ) (0.5, 0.5) (0.5,0.5)

c 复制代码

glTextCoord2f(0.5f, 0.5f);

通过正方形可求得内切圆的公式及半径 r = 0.5 r=0.5 r=0.5
( x − 1 2 ) 2 + ( y − 1 2 ) 2 = ( 1 2 ) 2 \Big(x-\frac{1}{2}\Big)^2+\Big(y-\frac{1}{2}\Big)^2=\Big(\frac{1}{2}\Big)^2 (x−21)2+(y−21)2=(21)2

将一个内切圆切36等分，其中每个弧度为 α = 2 π 36 = 10.4 1 ∘ \alpha=\frac{2\pi}{36}=10.41^\circ α=362π=10.41∘如下

c 复制代码

int n = 36;

圆的一周弧度为 2 π 把圆切 36 等分 ∴ α = 2 π 36 = π 18 ≈ 10.4 1 ∘ 圆的一周弧度为2\pi \\[8pt] 把圆切36等分 \\[8pt] \therefore \alpha=\frac{2\pi}{36}=\frac{\pi}{18}\approx10.41^\circ 圆的一周弧度为2π把圆切36等分∴α=362π=18π≈10.41∘

因此通过弧度和半径求得三角形上一个底点 B ( x B , y B ) B(x_B, y_B) B(xB,yB)
sin ⁡ α = h r , h = r sin ⁡ α y B = h + r = r sin ⁡ α + r cos ⁡ α = ∣ O D ∣ r , ∣ O D ∣ = r cos ⁡ α x B = ∣ O D ∣ + r = r cos ⁡ α + r ∴ B ( x B , y B ) = B ( r cos ⁡ α + r , r sin ⁡ α + r ) \sin\alpha=\frac{h}{r}, h=r\sin\alpha \\[8pt] y_B=h+r=r\sin\alpha+r \\[8pt] \cos\alpha=\frac{|OD|}{r}, |OD|=r\cos\alpha \\[8pt] x_B=|OD|+r=r\cos\alpha+r \\[8pt] \therefore B(x_B, y_B)=B(r\cos\alpha+r, r\sin\alpha+r) sinα=rh,h=rsinαyB=h+r=rsinα+rcosα=r∣OD∣,∣OD∣=rcosαxB=∣OD∣+r=rcosα+r∴B(xB,yB)=B(rcosα+r,rsinα+r)

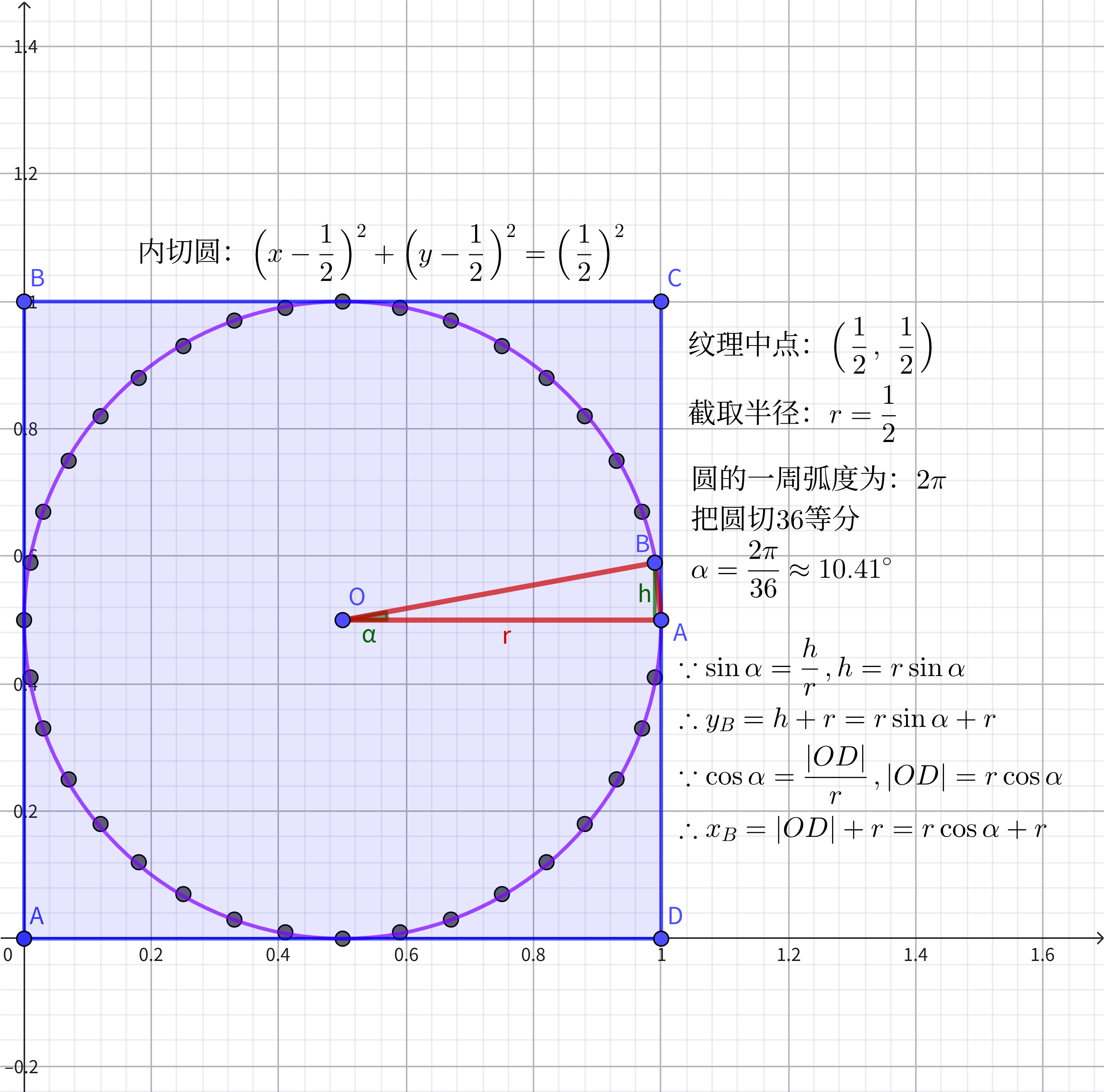
接着计算下一个点 B 2 ( x B 2 , y B 2 ) B_2(x_{B_2}, y_{B_2}) B2(xB2,yB2)，如下
y B 2 = ∣ O B 2 ∣ + r = r sin ⁡ 2 α + r x B 2 = ∣ O D 2 ∣ + r = r cos ⁡ 2 α + r ∴ B ( x B 2 , y B 2 ) = B ( r cos ⁡ 2 α + r , r sin ⁡ 2 α + r ) 因此，通式为： B n ( r cos ⁡ n α + r , r sin ⁡ n α ) , n ∈ N ∗ y_{B_2}=|OB_2|+r=r\sin2\alpha+r \\[8pt] x_{B_2}=|OD_2|+r=r\cos2\alpha+r \\[8pt] \therefore B(x_{B_2}, y_{B_2})=B(r\cos2\alpha+r, r\sin2\alpha+r) \\[8pt] 因此，通式为： \\[8pt] B_n(r\cos n\alpha+r, r\sin n\alpha), n \in N^* yB2=∣OB2∣+r=rsin2α+rxB2=∣OD2∣+r=rcos2α+r∴B(xB2,yB2)=B(rcos2α+r,rsin2α+r)因此，通式为：Bn(rcosnα+r,rsinnα),n∈N∗

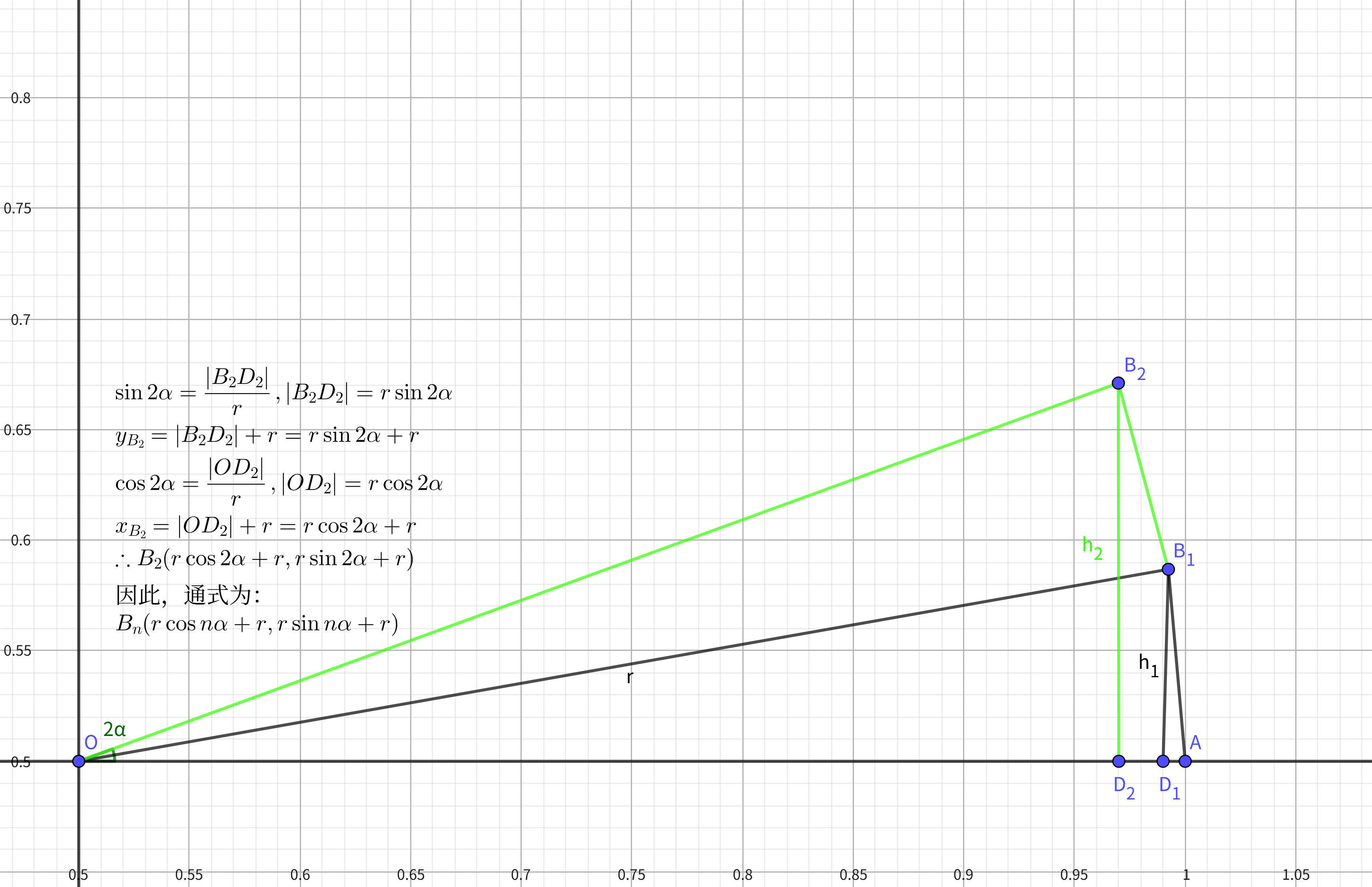
在代码中为

c 复制代码

// 启用二维纹理，调用特定编号的纹理
glEnable(GL_TEXTURE_2D);
// 绑定纹理
glBindTexture(GL_TEXTURE_2D, texture);
// 按照三角形截取，开始
glBegin(GL_TRIANGLE_STRIP);
// 将圆切36等分
int n = 36;
// 用于计算圆时的常量
double PI = 3.14159265358979323846;
// 显示长方形的四个顶点
for(int i = 0; i <= n; i++) {
	// 正方形中心的纹理坐标
	glTexCoord2f(0.5f, 0.5f);
	// 圆心的三维坐标
	glVertex3f(0.0f, 0.0f, 0.0f);
	// 内切圆中每个弧度值
	double a = 2 * PI / n * i;
	// 圆弧上点的纹理坐标
	glTexCoord2f(0.5f + 0.5f * cos(a), 0.5f + 0.5f * sin(a));

	// 圆弧的三维坐标
	glVertex3f(2.0f * cos(a), 2.0f * sin(a), 0.0f);
}
// 结束
glEnd();
// 关闭纹理贴图
glDisable(GL_TEXTURE_2D);

正方体材质贴图

正方体有八个顶点，并且给八个顶点进行编号

序号	顶点	坐标
0	A	(-1, -1, -1)
1	B	(+1, -1, -1)
2	C	(+1, +1, -1)
3	D	(-1, +1, -1)
4	A₁	(-1, -1, +1)
5	B₁	(+1, -1, +1)
6	C₁	(+1, +1, +1)
7	D₁	(-1, +1, +1)

八个顶点组合成六个面：

四边形	编号	数组
ABCD	{0, 1, 2, 3}	square[0]
A₁B₁C₁D₁	{4, 5, 6, 7}	square[1]
AA₁BB₁	{0, 4, 1, 5}	square[2]
BB₁CC₁	{1, 5, 2, 6}	square[3]
CC₁DD₁	{2, 6, 3, 7}	square[4]
DD₁AA₁	{3, 7, 0, 4}	square[5]

假设C语言没有Map集合概念

c 复制代码

// 八个顶点
int dots[8][3] = {
	{-1, -1, -1}, {+1, -1, -1}, {+1, +1, -1}, {-1, +1, -1},
	{-1, -1, +1}, {+1, -1, +1}, {+1, +1, +1}, {-1, +1, +1}
};
// 六个面
int square[6][4] = {
	{0, 1, 2, 3}, {4, 5, 6, 7}, {0, 4, 1, 5},
	{1, 5, 2, 6}, {2, 6, 3, 7}, {3, 7, 0, 4}
};

但正方体每个面都有方向，所以可以规定正对(垂直看)其中正方体一个面的左下点对应正方形纹理的 ( 0 , 0 ) (0, 0) (0,0)点，正方体一个面的右上点对应正方形纹理的 ( 1 , 1 ) (1, 1) (1,1)，如下：

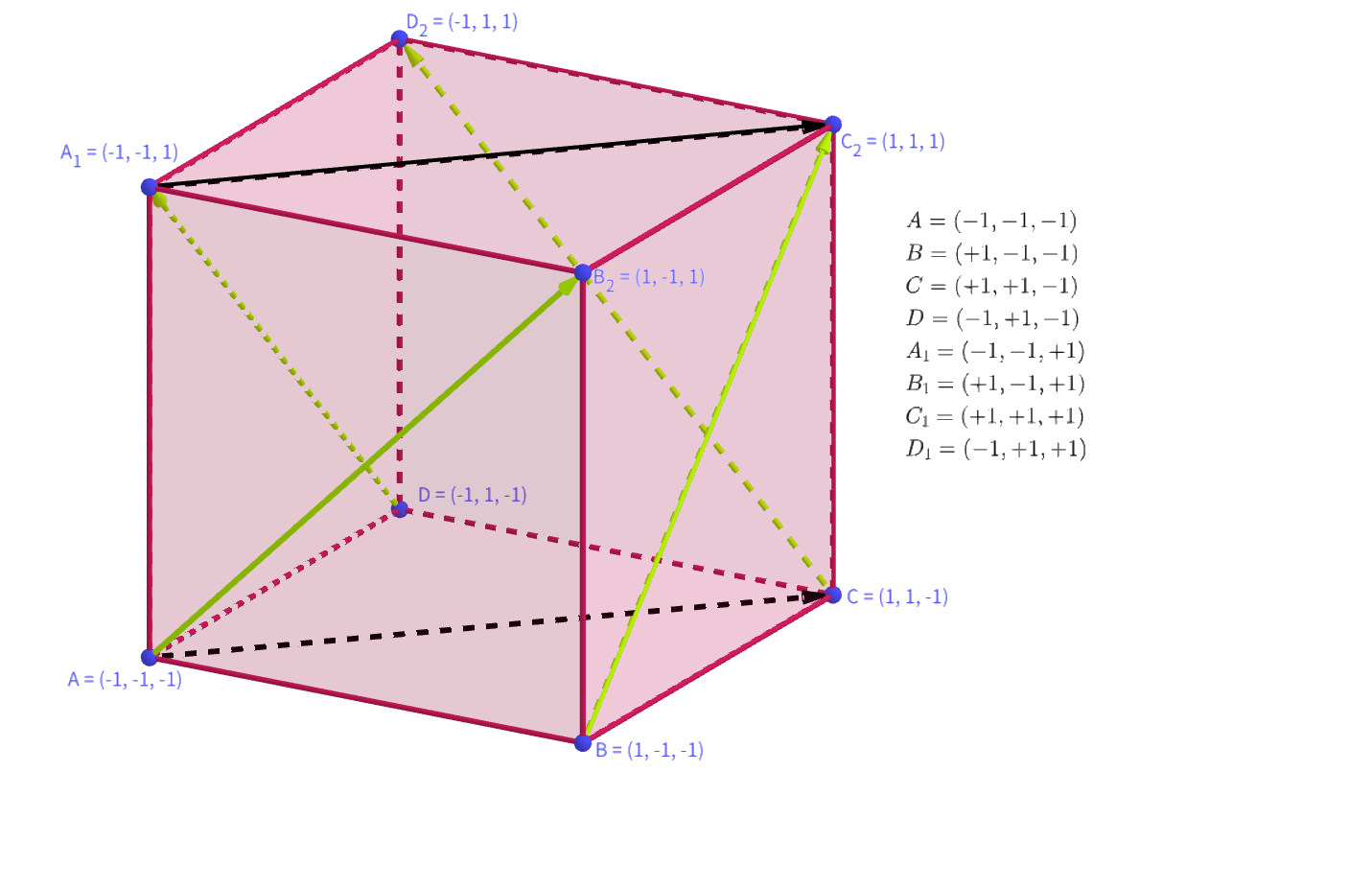
正方形纹理一个点分别对应正方体6个面中一个点，或者正方体6个面中一个面分别对应正方形纹理中四个点，共右24组对应关系，所以使用for循环进行纹理粘贴

c 复制代码

for(int i = 1; i < 6; i++) {
	// 启用二维纹理，调用特定编号的纹理
	glEnable(GL_TEXTURE_2D);
	// 绑定箱子的纹理
	glBindTexture(GL_TEXTURE_2D, texture);
	// 按照四边形截取，开始
	glBegin(GL_QUADS);
	// 获取其中一个面, 例如：ABCD={0, 1, 2, 3}
	int array[4] = square[i];
	
	glTextCoord2f(0. 0);
	// 获取其中一个序号，根据序号找到一个点，例如array[0]=0, dots[0]={-1, -1, -1}
	// 之后根据这个点的下标找其中一个值如：dots[0][0]=-1
	glVertex3f(
		dots[array[0]][0],
		dots[array[0]][1],
		dots[array[0]][2]
	);

	glTextCoord2f(1. 0);
	glVertex3f(
		dots[array[1][0],
		dots[array[1][1],
		dots[array[1][2]
	);

	glTextCoord2f(1, 1);
	glVertex3f(
		dots[array[2]][0],
		dots[array[2]][1],
		dots[array[2]][2],
	);

	glTextCoord2f(0, 1);
	glVertex3f(
		dots[array[3]][0],
		dots[array[3]][1],
		dots[array[3]][2],
	);
}
// 关闭纹理贴图
glEnd();
glDisable(GL_TEXTURE_2D);