本节开始讲解SLAM中一个非常重要的知识点，相对位姿约束或者GTSAM中称为Between Factor, 其主要应用于位姿图中的相邻两帧间的约束以及回环约束，如下图所示
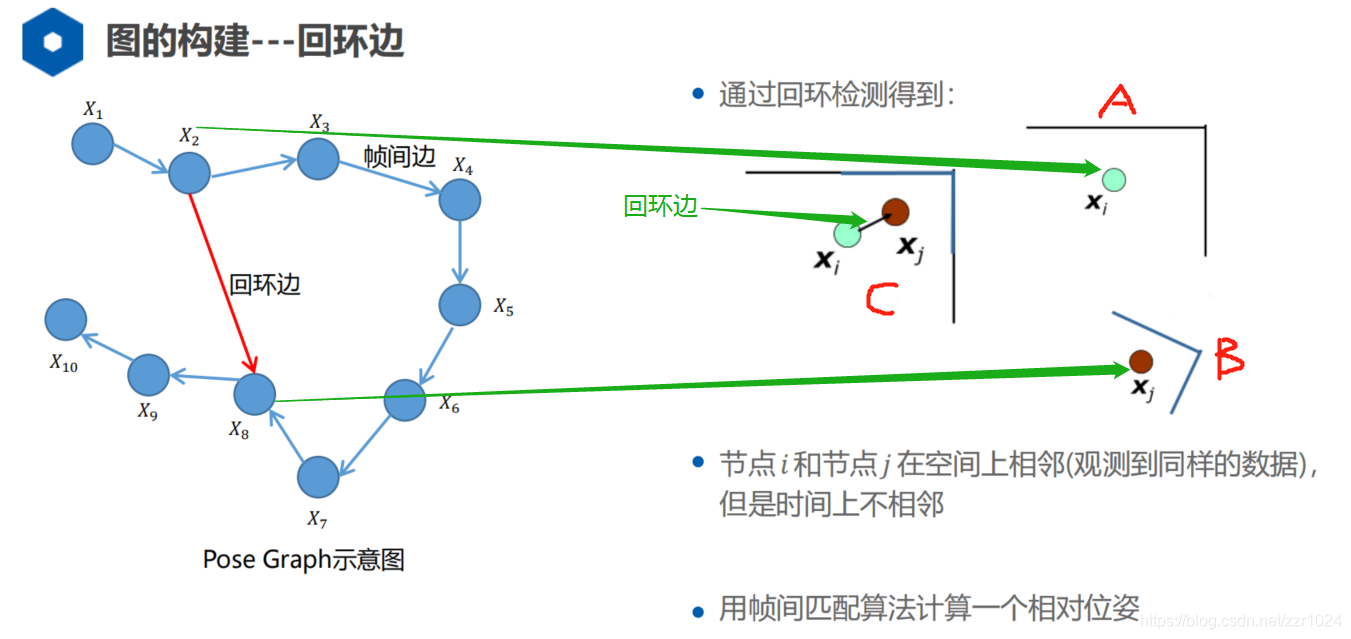
上图中，相邻两个节点间的约束跟红色回环约束即为相对位姿约束的主要应用场景；从本节开始到之后的几节，均会讲解该约束的残差跟雅可比求解，当然会以不同的方式来推导，自动求导跟数值求导不作为重点讲解，因为他们不具有差异性，各种雅可比的求解都差不多，另外本节将以李代数跟四元数作为旋转的表示，至于欧拉角跟轴角看后边时间，因为本系列博客还有大量内容没有展示，接下来请看精彩内容，首先以李群李代数视角来讲解，这部分内容来源于《SLAM十四讲》
一. 基础知识
完整版BCH形式
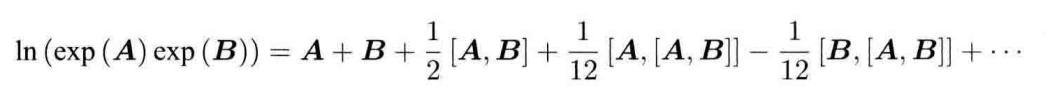
忽略二阶项
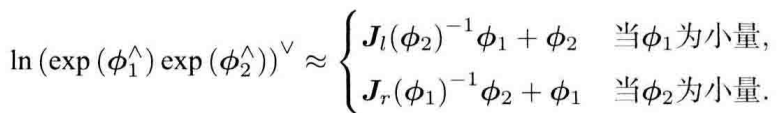
二. 问题描述 
我们取李代数的表示形式
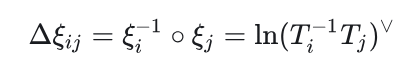
或者李群的写法：
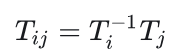
事实上，上式不会严格成立，存在一个误差项
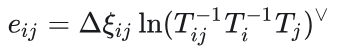
从上式以及图中可以看到，相对位姿约束连接着两个顶点（待估计的状态量），因此其雅可比也应该是两项，此处为了一次性求解两项，给Ti跟Tj分别乘以左扰动，则
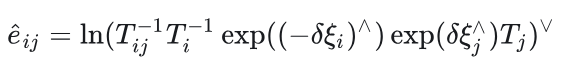
该式中，两个扰动项被加载了中间。为了利用BCH近似 ，我们希望把扰动项移到式子左侧或者右侧，这里先给出伴随性质的结论
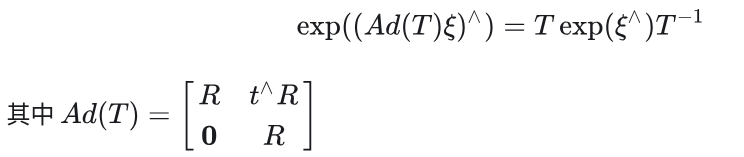关于证明参见附录；
对伴随性质两边同乘以矩阵T可得
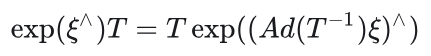
该式表明，通过引入一个伴随项，能够"交换"扰动项左右侧的T 。利用伴随，可以将扰动挪到最右边（或者最左边），导出右乘形式的雅可比矩阵（挪到左边时形成左乘）
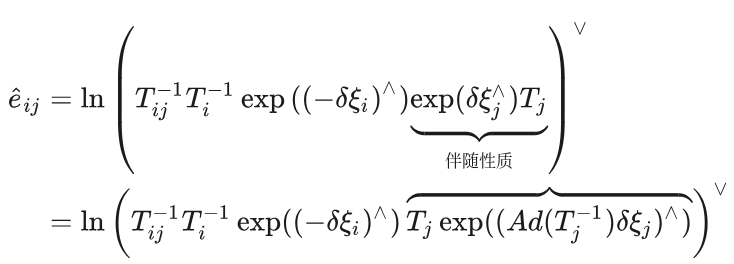
补充证明方法一：
关于上述倒数第三行 到 倒数第二行， 使用了两次泰勒展开 ，由于是微小量，所以二次以上的i和j交叉项以及自身的二阶项均可忽略不计：
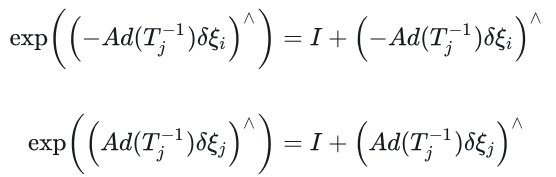
倒数第二行 到 倒数第一行的推导
李代数x的李群表达式为何能这么设置？因为实际的表达是如下形式，而上式正好是下面这个的一阶近似
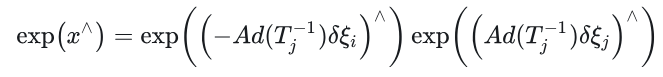
这个式子的含义是，两个SE3矩阵相乘结果依然是SE3, 满足的是群的封闭性
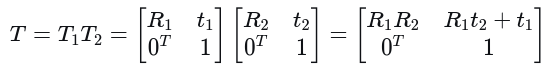
这里已经推导出来了误差函数的表达式了，但是还差个x不知道具体形式是什么，接下来推导下：
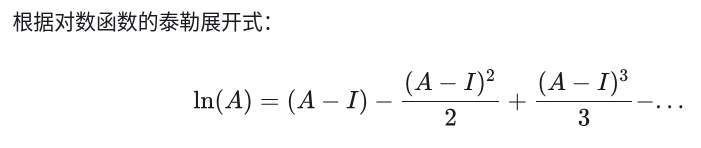
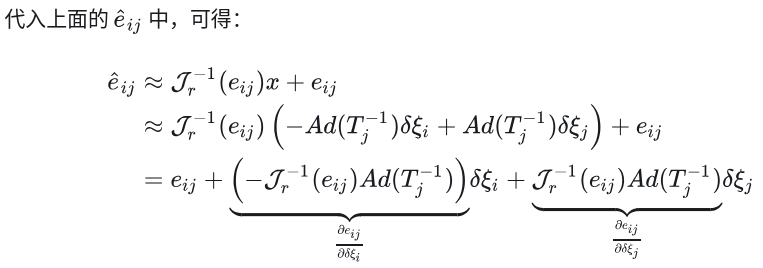
补充证明方法二：
还是先得到误差项的倒数第三行：
根据十四讲第4讲4.3.1小节 中的BCH近似公式(4.29)可得：
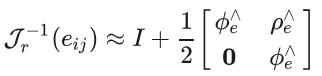
注意：上述右雅可比的逆放入附录（3），并且上述左乘扰动还是过于复杂，下一讲用更简单的方法来推导
二. 代码展示
- 右雅克比的逆
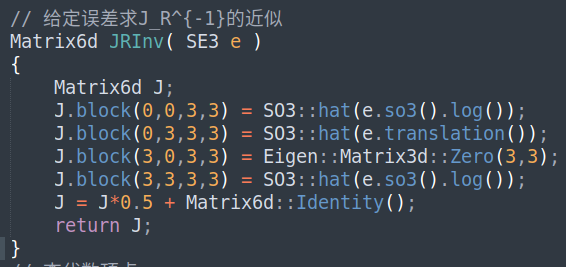
- 误差函数
- 位姿图雅可比定义
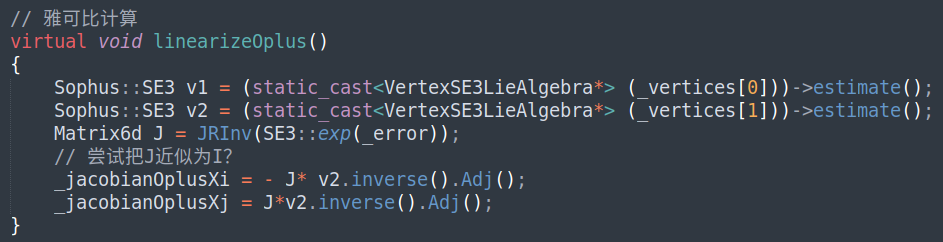
总结
本节详细推导了位姿图残差及雅可比矩阵，采用了同时扰动i， j两时刻的位姿，主要采用了左乘扰动推导了雅可比的形式，但推导过于复杂，下一节将展示更简洁的左乘雅可比的形式。
附录：
（1）伴随性质证明：
伴随矩阵如下：
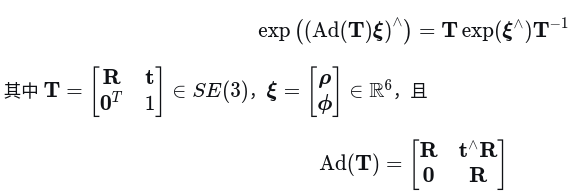
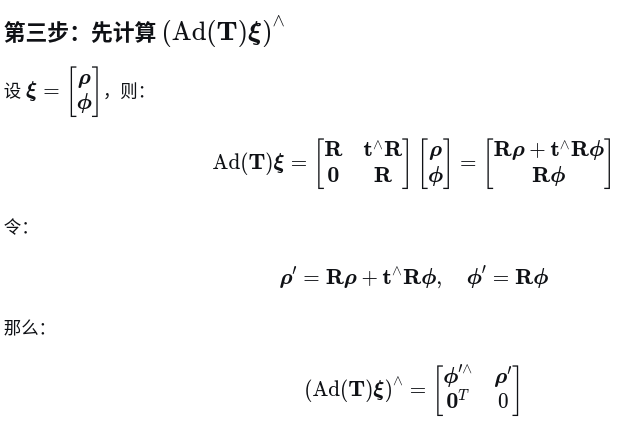
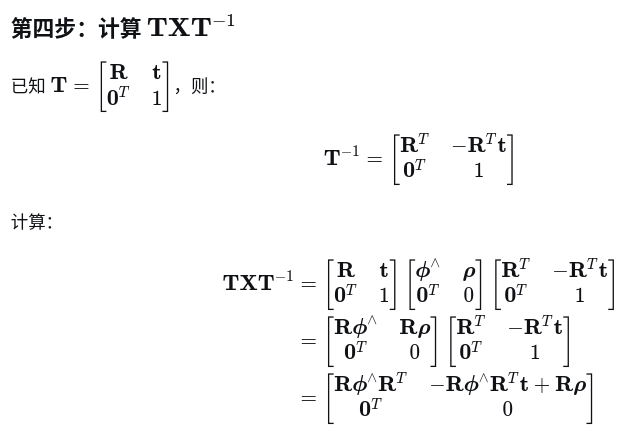
先看旋转部分
SO(3)的性质，在附录（2）中证明
再看平移部分
先给出个公式
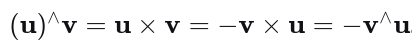
根据上述计算，平移部分为：
（2）伴随性质证明：
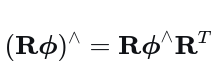
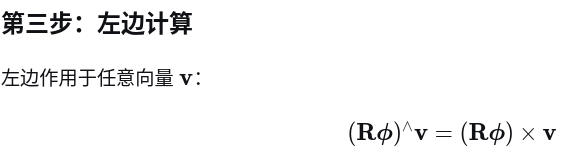
（3）SE(3) 的左右雅可比矩阵及其逆
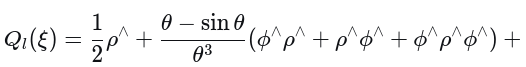
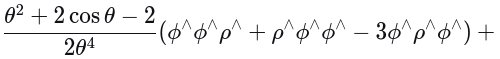
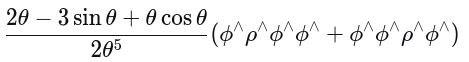
上述形式与前面推导的形式差别咋那么的大？
实际上这里的是精确形式，前边是一阶近似，现在来看下，怎么推导的右雅可比的逆的近似
