目录
---
1.摘要
本文提出了一种面向高维复杂工程优化的优先级驱动粒子群算法 PDPSO,算法通过去除惯性项的优先级搜索机制与自适应动态候选解管理,实现了无需变异算子的稳定高效搜索,并在探索与开发之间保持自平衡。PDPSO 在 CEC2017 高维测试与 34 个工程案例中均展现出高精度、强鲁棒性和低维度敏感性。
2.基于优先级驱动搜索、具备动态候选解管理策略的粒子群算法PDPSO
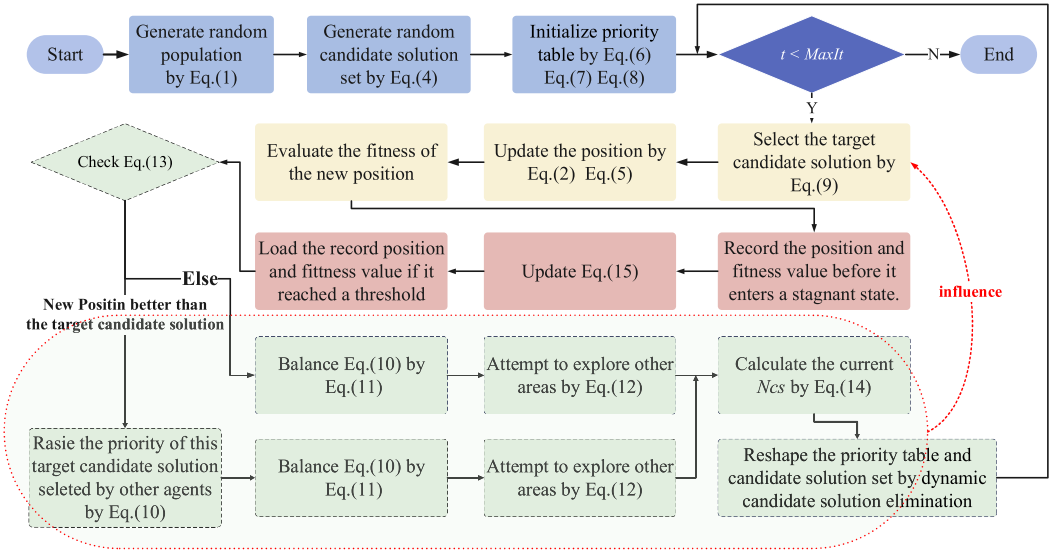
PDPSO 通过融合优先级驱动搜索与动态候选解管理,使算法能够更高效、稳定地利用更多参考信息,从而将计算资源更有效地转化为优化能力。蓝色为原始 PSO 框架,黄色表示优先级驱动搜索,红色表示状态回退机制,绿色表示除回退外的动态候选解管理部分。
优先级驱动搜索策略
在 PDPSO 中,通过维护一个高质量候选解集合 CS 来引导粒子的搜索方向,从而实现更有效的优化搜索。
C S = { C S j k ∣ j = 1 , 2 , ⋯ , N c s k } CS=\left\{CS_j^k|j=1,2,\cdots,Ncs^k\right\} CS={CSjk∣j=1,2,⋯,Ncsk}
PDPSO 通过维护自适应候选解集 C S CS CS ,并为每个个体设定独立的优先级,从而以高优先级候选解替代传统 PSO 的全局最优。算法通过跨迭代选择不同候选解来保持多样性,因此去除惯性项,并仅由个体最优与高优先级候选解共同决定速度更新,以获得更稳定且有效的搜索。
v i k + 1 = c 1 r 1 ( p b i k − x i k ) + c 2 r 2 ( C S i ( k ) k − x i k ) \boldsymbol{v}_i^{k+1}=c_1\boldsymbol{r}_1\left(\boldsymbol{p}\boldsymbol{b}_i^k-\boldsymbol{x}_i^k\right)+c_2\boldsymbol{r}2\left(\boldsymbol{C}\boldsymbol{S}{i(k)}^k-\boldsymbol{x}_i^k\right) vik+1=c1r1(pbik−xik)+c2r2(CSi(k)k−xik)
动态候选解决方案管理策略
PDPSO 的动态候选解管理策略通过随机初始化候选解集,并依托优先级矩阵为粒子分配个性化的学习对象。优先级由成功提升、过度学习惩罚和低优先候选解回补三机制共同调控,实现探索与开发的自平衡。候选解内容按优胜替换原则更新,其容量随迭代递减并删除最差候选解,使算法逐步从多样探索过渡到集中开发。为避免后期因容量缩减陷入局部,PDPSO 引入自适应状态回退机制,使停滞粒子回到有效状态并降低相关候选解优先级,从而保持搜索活性并增强跳出局部最优的能力。
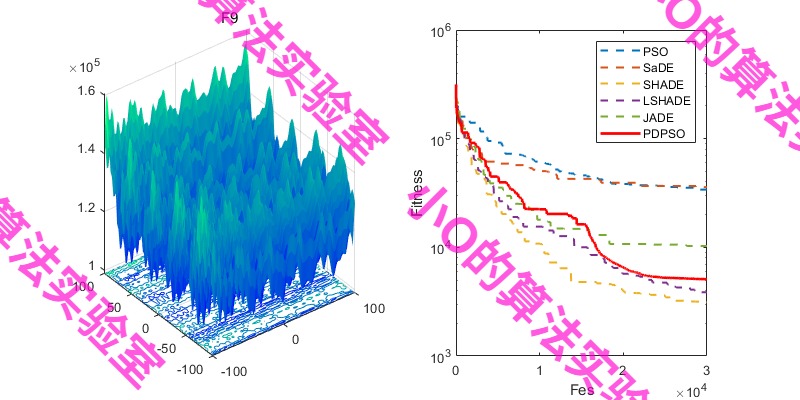
3.结果展示
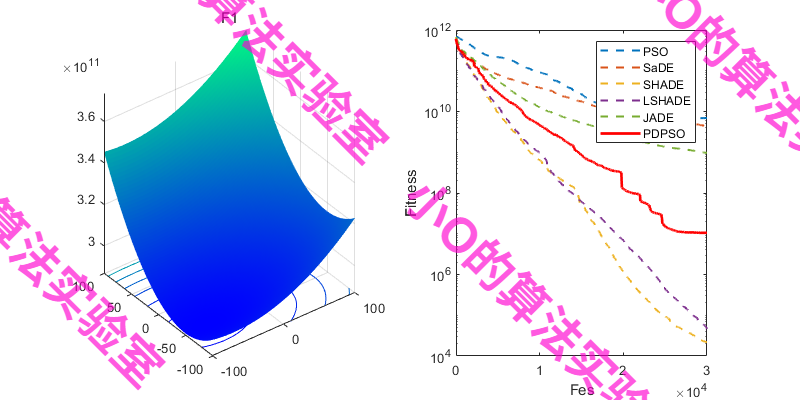
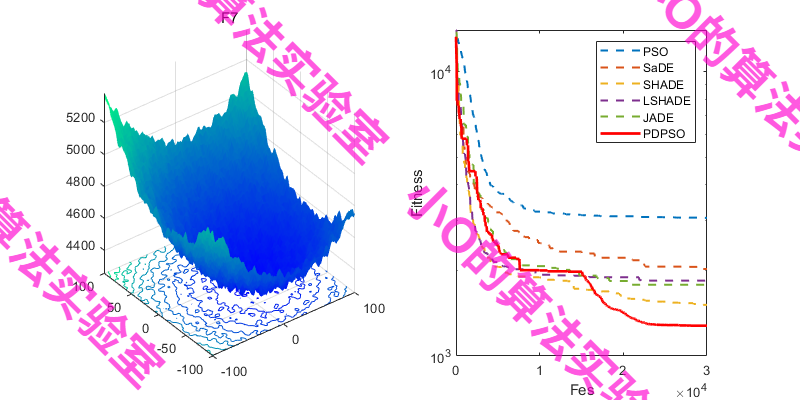
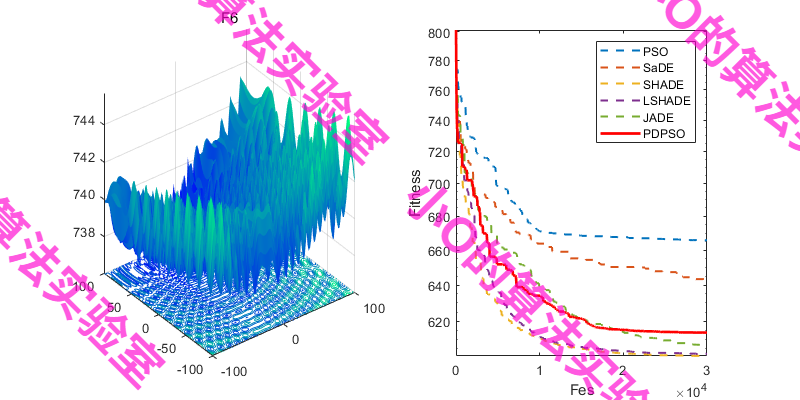
4.参考文献
1\] Hu G, He P, Jia H, et al. PDPSO: Priority-driven search particle swarm optimization with dynamic candidate solutions management strategy for solving higher-dimensional complex engineering problems\[J\]. Computer Methods in Applied Mechanics and Engineering, 2025, 446: 118318. ### 5.代码获取 xx ### 6.算法辅导·应用定制·读者交流 xx