力扣每日一题（11.10-11.29）0-1 和 k 整除系列

目录

[2872. 可以被 K 整除连通块的最大数目 树上问题](#2872. 可以被 K 整除连通块的最大数目 树上问题)

[3542. 将所有元素变为 0 的最少操作次数 -- 单调栈](#3542. 将所有元素变为 0 的最少操作次数 -- 单调栈)

[2654. 使数组所有元素变成 1 的最少操作次数 -- gcd](#2654. 使数组所有元素变成 1 的最少操作次数 -- gcd)

[474. 一和零 0-1背包](#474. 一和零 0-1背包)

[3228. 将 1 移动到末尾的最大操作次数 思路题建模为 堵车](#3228. 将 1 移动到末尾的最大操作次数 思路题建模为 堵车)

[3381. 长度可被 K 整除的子数组的最大元素和 -- 同余前缀和](#3381. 长度可被 K 整除的子数组的最大元素和 -- 同余前缀和)

---

2872. 可以被 K 整除连通块的最大数目 树上问题

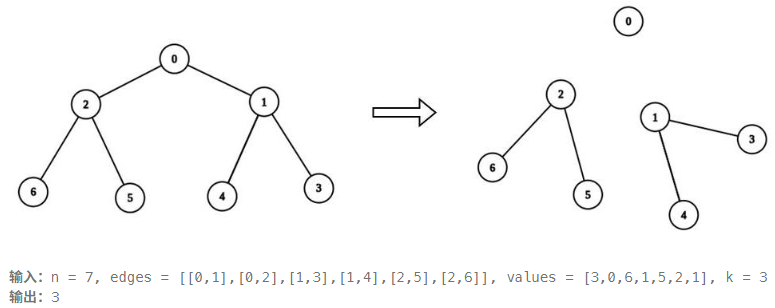
把树分为尽量多的联通块，每个联通块求和值都是 k 的倍数。

又因为一个值不是 k 倍数的联通块，一定无法划分成 若干个 值都是 k 倍数的。

所以每次切割需要从 一个 k倍数，划分为 两个 k倍数。

树上搜索时，如果子树是 k 的倍数，说明可以把这条边断掉。（答案即为 断掉的边数+1）

class Solution:
    def maxKDivisibleComponents(self, n: int, edges: List[List[int]], values: List[int], k: int) -> int:
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)

        # 返回子树 x 的点权和
        def dfs(x: int, fa: int) -> int:
            s = values[x]
            for y in g[x]:
                if y != fa:
                    s += dfs(y, x)  
            nonlocal ans
            ans += s % k == 0 # 子树是倍数，可以断，统计答案
            return s

        ans = 0
        dfs(0, -1)
        return ans

3542. 将所有元素变为 0 的最少操作次数 -- 单调栈

每次可以选一个区间，把其中最小值都置零 。问变成全0的最小操作次数。

策略：第一次我选整个区间 ，这些最小值对应的 0 把数组分成了一个个小段 ，后续再对小段操作。

比如 nums = [1,2,3,3,2,1] 我操作到 3 发现 33 左右的2 都小于3.

所以操作 2 的时候会把 3,3 分成一个小段，再操作 3,3。

我维护一个单调栈 [1,2,3] 再加入 3 可以和前面的 3 合并一起操作。

再加入 2 则发现 3 需要一个操作，把 3 出栈，加入的 2 和 栈顶的 2 抵消。

总结：先出栈 栈顶大于 a 的都弹出 ；栈顶元素小于 a 则入栈。

（得到的栈一直是单调递增的）

最后还需出栈次数为 st 的非零元素个数。

class Solution:
    def minOperations(self, nums: List[int]) -> int:
        ans,st = 0, []

        for x in nums:
            while st and x < st[-1]: # 出栈
                st.pop()
                ans += 1
            if not st or x != st[-1]: # 和栈顶元素不一样，则进栈
                st.append(x)

        return ans + len(st) - (st[0] == 0)

2654. 使数组所有元素变成 1 的最少操作次数 -- gcd

假设数组里有 1，1可以把相邻的数都置为 1 ，答案即为 n-cnt1。

否则，就需要用最小的步数（最短的序列）构造 gcd = 1，然后用这个 1 扩展序列。

假设数组内所有数的 gcd > 1，则输出 -1.

class Solution:
    def minOperations(self, nums: List[int]) -> int:
        if gcd(*nums) != 1:
            return -1
        n, cnt1 = len(nums), sum(x==1 for x in nums)
        if cnt1:
            return n-cnt1

朴素：二重循环求每个位置开始 最短使得 gcd=1 的长度。

最后的答案即为 n - 1 + （minn - 1）

minn = n
for i in range(n):
    g = 0
    for j in range(i, n):
        g = gcd(g, nums[j])
        if g == 1:
            minn = min(minn, j - i)
            break
return minn + n - 1

如果发掘出 gcd 的 log 性质，一个数的因数个数是很少的 log 级别的：

每次枚举右端点 ，带上左端点的，可能的前缀 gcd 可能数是 log 级别的，

循环的前一维度 可以由 n -> logn

维护数组 g；从当前位置往前 gcd 的值，与对应的最右边（序列最短）的位置。

（往左加数 序列变长 gcd变小）

比如 [2,6,3,4] 算例，

2,6\] 对应的 g 为 \[2,0\], \[6,1

2,6,3\] -\>\[1,3,3\] 对应的 g 为 \[1,0\], \[3,2

2,6,3,4\] -\>\[1,1,1,4\] 对应的 g 为 \[1,4\], \[4,3

每次更新时，先在尾巴添加自己的位置。对前面的 gcd 一遍，

如果重复可合并，利用快慢指针原地合并。

min_size = n
a = []  # [GCD，相同 GCD 闭区间的右端点]
for i, x in enumerate(nums):
    a.append([x, i])

    # 原地去重，因为相同的 GCD 都相邻在一起
    j = 0 # j 代表慢指针的头
    for p in a:
        p[0] = gcd(p[0], x)
        if a[j][0] != p[0]: # 不同则加新的 gcd
            j += 1
            a[j] = p
        else:
            a[j][1] = p[1] # 相同则更新当前慢指针对应的位置
    del a[j + 1:]

    if a[0][0] == 1:
        # 这里本来是 i-a[0][1]+1，把 +1 提出来合并到 return 中
        min_size = min(min_size, i - a[0][1])
return min_size + n - 1

474. 一和零 0-1背包

找出并返回 strs 的最大子集 的长度，该子集中 最多 有 m 个 0 和 n 个 1。

可把 0和1 看做两个维度的容量，用 s.count('0') 得到小串 s 中 0 的个数。

只能选一次的 0-1 背包从后往前倒过来更新，

优化：先算一下倒过来的上限，即为前面累积的 0-1 个数。

class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        f = [[0] * (n + 1) for _ in range(m + 1)]
        sum0 = sum1 = 0
        for s in strs:
            cnt0 = s.count('0') # 字符串 0-1 个数
            cnt1 = len(s) - cnt0
            sum0 = min(sum0 + cnt0, m) # 优化前几个时的更新上限
            sum1 = min(sum1 + cnt1, n)
            for j in range(sum0, cnt0 - 1, -1):
                for k in range(sum1, cnt1 - 1, -1):
                    f[j][k] = max(f[j][k], f[j - cnt0][k - cnt1] + 1)
        return max(map(max, f))

3228. 将 1 移动到末尾的最大操作次数 思路题建模为 堵车

选一个 s[i] == '1' 且 s[i + 1] == '0' 的下标 i ，把 1 往右移动直到末尾 or 下一个 1。

可以看做一个移车问题：

最小 操作次数：从后往前看，每次把最后一个需要移的车移到末尾。

最大 操作次数，每次都移最前面 可以移的那辆，导致"堵车"

class Solution:
    def maxOperations(self, s: str) -> int:
        ans, cnt = 0, 0
        for i,a in enumerate(s):
            if a == '1':
                cnt += 1
            elif i > 0 and s[i-1] == '1':
                ans += cnt
        return ans

3381. 长度可被 K 整除的子数组的最大元素和 -- 同余前缀和

限定长度为 k 的倍数 ；枚举右端点，则左端点的下标必须和右端点对 k 同余。

前缀和，区间 = 右端前缀和 - 左端前缀和；维护、减去最小的同余位置前缀和。

class Solution:
    def maxSubarraySum(self, nums: List[int], k: int) -> int:
        min_s = [inf] * k # 同余位置前缀和
        min_s[-1] = s = 0
        maxn = -inf
        for j, x in enumerate(nums):
            s += x # 当前前缀和
            i = j % k
            # 更新最大值和同余位置
            maxn = max(maxn, s - min_s[i])
            min_s[i] = min(min_s[i], s)
        return maxn