目录

1.摘要
大规模定制是现代商业环境中的重要战略,而柔性作业车间因其高度灵活性,尤其适合应用于大规模定制。因此,柔性作业车间调度问题(FJSP)近年来得到了广泛关注。为解决FJSP,研究者提出了多种智能算法,并通过BRdata、BCdata和DPdata等基准测试评估其性能。然而,许多基准实例仍未得到有效解决。本文提出了一种混合遗传禁忌搜索算法(HGTSA)来进一步解决这些基准问题,其设计了一种能够同时表示机器选择和操作顺序的编码方式。在遗传算法阶段,提出了两种专门的交叉算子,确保种群多样性;同时,设计了两种变异算子,防止算法过早陷入局部最优解。在禁忌搜索阶段,提出了融合N8和k-insertion邻域结构的混合邻域结构,增强了局部搜索能力。
2.问题描述
柔性作业车间调度问题(FJSP)旨在为每个操作分配合适的机器,并确定处理顺序,最小化最大完成时间(Makespan)。FJSP的假设包括每个操作只能由一台机器处理,作业间不考虑运输和设置时间,且操作一旦开始不能中断。数学模型通过一系列符号和决策变量来描述,目标是最小化Makespan,并通过一系列约束确保操作的顺序和机器的分配。
FJSP可通过析取图模型表示,其中节点表示操作,弧表示操作间的关系。该模型的关键路径是从虚拟开始到结束操作的最长路径,路径长度即为Makespan。FJSP的析取图需要在选择机器时同时考虑每个操作的机器信息。
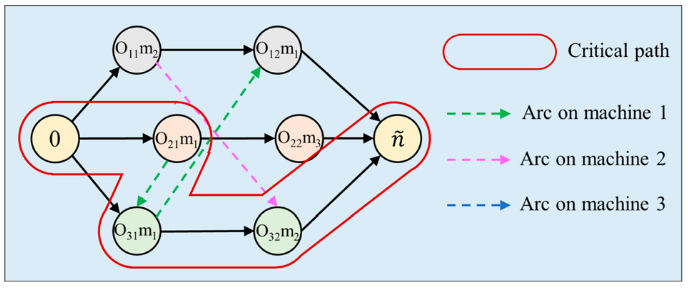
3.HGTSA for FJSP
本文提出的混合遗传禁忌搜索算法(HGTSA)结合了遗传算法(GA)和禁忌搜索(TS)的优势,旨在解决柔性作业车间调度问题(FJSP)。通过整合 N8 和 k-insertion 邻域结构,HGTSA 提高了全局搜索和局部优化能力。
编解码方案
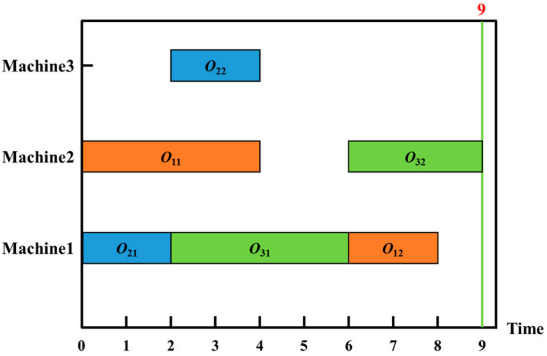
在HGTSA算法中,采用基于析取图的编码方法,通过确定每个操作在每台机器上的处理顺序来获得相应的调度方案。每个染色体包含 m m m个字符串,每个字符串对应一台机器,表示该机器上作业的处理顺序,每个元素为一个介于[1,n]范围内的整数。由于FJSP的每个操作可以在多台机器上处理,因此每个字符串的长度会有所不同。
假设染色体为 [(2 3 1) (1 3) (2)],其中 (2 3 1)、(1 3) 和 (2) 分别表示机器1、机器2和机器3上作业的处理顺序,对应的甘特图如图所示。
交叉算子
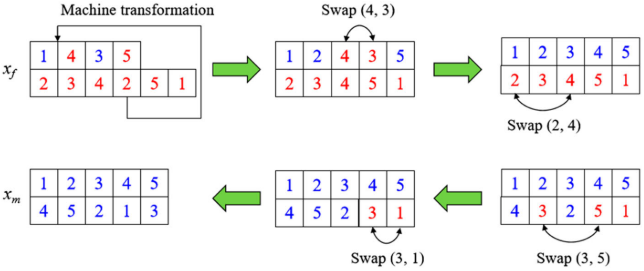
在HGTSA中,交叉操作通过构建父代个体之间的变换路径生成多个子代个体。首先,选择两个父代个体 x f x_f xf和 x m x_m xm,通过迭代改变操作的处理机器或交换操作位置,逐步将 x f x_f xf转化为 x m x_m xm,并沿变换路径生成候选子代。由于作业和机器数量增加,路径上会生成大量候选解,因此仅选择部分解进行禁忌搜索,每进行α次交换选择当前解,每进行β次交换继续选择,直到达到 x m x_m xm。若生成不可行解,则采用方法将其转为可行解。
变异算子
HGTSA中设计了两种变异算子以帮助个体跳出局部最优。第一种通过交换关键路径上两个连续操作的位置生成新解,第二种通过将操作随机分配到不同的机器上修改关键路径。
禁忌搜索(TS)
HGTSA 中通过引入禁忌搜索(TS)增强局部搜索能力,结合 N8 和 k-insertion 两种邻域结构优化关键路径,从而减少 makespan。N8 邻域结构:通过改变同一机器上关键操作的位置,扩大搜索空间。k-insertion 邻域结构:通过改变关键操作的处理机器来重构关键路径,优化调度。
4.结果展示

5.参考文献
1\] Xie J, Teng Y, Gao L, et al. An efficient and stable intelligent scheduling algorithm based on hybrid neighbourhood structure for flexible job shop scheduling problem benchmarks\[J\]. International Journal of Production Research, 2025: 1-15. ### 6.代码获取 xx ### 7.算法辅导·应用定制·读者交流 xx