LSTM 深度解析：原理、实现与实战应用

引言：序列数据处理的革命性突破

在深度学习的发展历程中，循环神经网络（Recurrent Neural Network, RNN）曾被寄予厚望，它通过引入循环结构，理论上能够捕捉序列数据中的时序依赖关系，为自然语言处理、时间序列预测等领域提供了新的解决方案。然而，传统 RNN 在实际应用中面临着严峻的挑战 ------ 梯度消失（Vanishing Gradient）和梯度爆炸（Exploding Gradient）问题。当处理长序列数据时，梯度在反向传播过程中会急剧衰减或无限增大，导致模型无法学习到长期依赖关系，训练效果大打折扣。

为解决这一核心痛点，Hochreiter & Schmidhuber 于 1997 年提出了长短期记忆网络（Long Short-Term Memory, LSTM）。LSTM 通过独特的门控机制（Gating Mechanism），能够自适应地调节信息的存储与遗忘，有效缓解了梯度消失问题，成为处理序列数据的主流模型。如今，LSTM 已广泛应用于机器翻译、语音识别、情感分析、股价预测等众多领域，深刻改变了人工智能对时序信息的处理方式。

本文将从 LSTM 的核心原理出发，深入剖析其数学模型与门控机制，详细讲解基于 TensorFlow 和 PyTorch 的双框架代码实现，并通过时间序列预测和文本分类两个实战案例，帮助读者全面掌握 LSTM 的理论与应用。全文约 6000 字，兼顾理论深度与实践可行性，适合深度学习初学者、算法工程师及相关领域研究人员参考。

一、LSTM 的核心原理：门控机制与结构解析

1.1 传统 RNN 的局限性

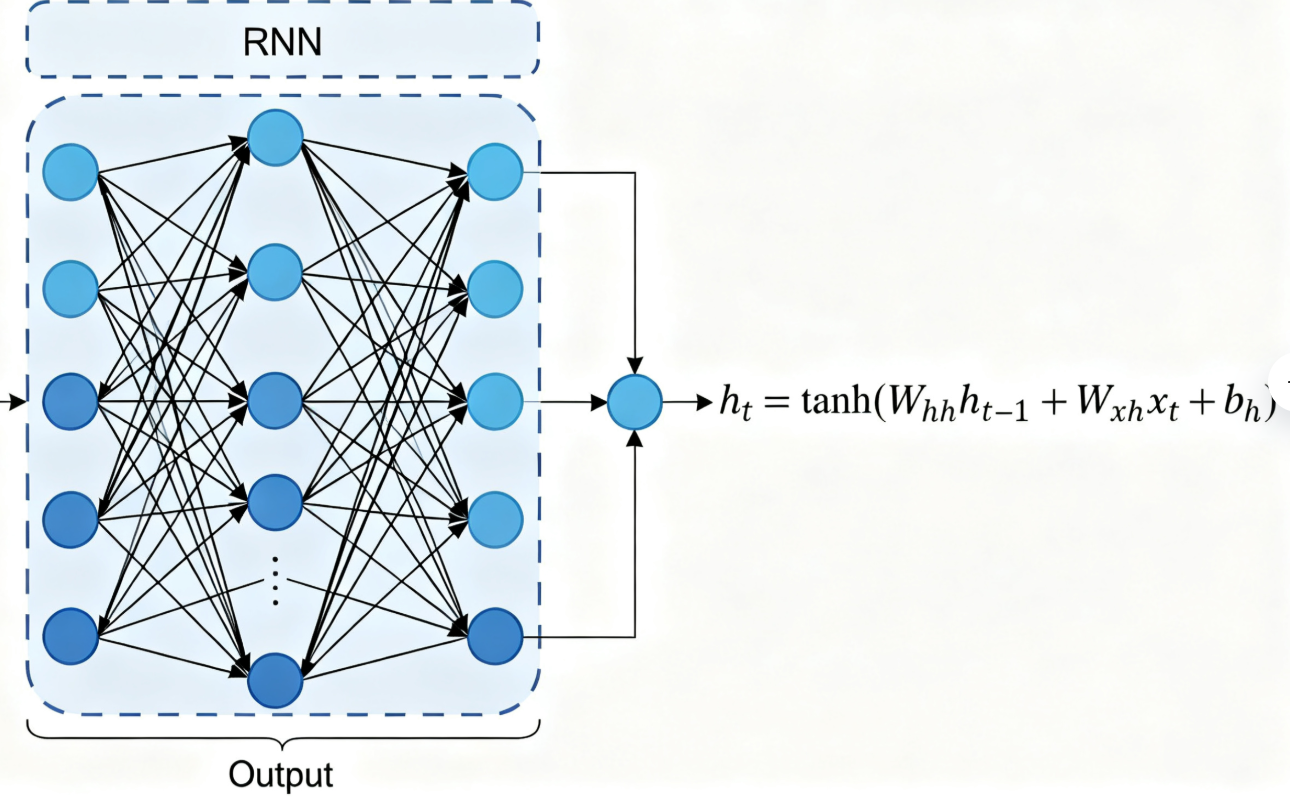
要理解 LSTM 的创新之处，首先需要回顾传统 RNN 的结构与缺陷。传统 RNN 的核心是循环单元（Recurrent Unit）

传统 RNN 的前向传播公式如下：

隐藏状态更新：\(h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b_h)\)

输出层计算：\(y_t = \sigma(W_{hy}h_t + b_y)\)

其中，\(x_t\)为\(t\)时刻的输入，\(h_t\)为\(t\)时刻的隐藏状态，\(y_t\)为\(t\)时刻的输出，\(W_{hh}\)、\(W_{xh}\)、\(W_{hy}\)为权重矩阵，\(b_h\)、\(b_y\)为偏置项，\(\tanh\)为激活函数，\(\sigma\)为 sigmoid 激活函数（用于分类任务）。

在反向传播过程中，梯度需要通过时间步反向传播（BPTT, Backpropagation Through Time）。对于长序列，梯度会经过多个时间步的乘积运算：

\(\frac{\partial Loss}{\partial W_{hh}} = \sum_{t=1}^T \frac{\partial Loss}{\partial h_t} \cdot \frac{\partial h_t}{\partial h_{t-1}} \cdot \frac{\partial h_{t-1}}{\partial W_{hh}}\)

由于\(\tanh\)函数的导数取值范围为\((0,1]\)，当时间步\(T\)较大时，多个小于 1 的梯度相乘会导致梯度呈指数级衰减（梯度消失）；若权重矩阵\(W_{hh}\)的特征值大于 1，则会导致梯度呈指数级增长（梯度爆炸）。梯度消失会使模型无法更新早期时间步的参数，无法学习长期依赖；梯度爆炸则会导致参数更新溢出，模型训练崩溃。

1.2 LSTM 的核心创新：门控机制

LSTM 的核心突破在于引入了门控机制 和细胞状态（Cell State），通过三个独立的门（遗忘门、输入门、输出门）来调节信息的流动与存储，从而解决梯度消失问题。

1.2.1 细胞状态（Cell State）

LSTM 引入了一个与隐藏状态并行的细胞状态\(c_t\)，其作用类似于 "记忆通道"，能够长期存储序列信息。与隐藏状态不同，细胞状态的更新采用加法运算而非乘法运算，梯度在反向传播时可以直接通过细胞状态传递，有效避免了梯度的指数级衰减。细胞状态的更新公式为：

\(c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t\)

其中，\(\odot\)表示元素 - wise 乘法，\(f_t\)为遗忘门输出，\(i_t\)为输入门输出，\(\tilde{c}_t\)为候选细胞状态。

1.2.2 遗忘门（Forget Gate）

遗忘门的作用是决定是否保留上一时刻的细胞状态信息，其输出\(f_t\)的取值范围为\([0,1]\)（通过 sigmoid 激活函数实现）。当\(f_t=1\)时，完全保留上一时刻的细胞状态；当\(f_t=0\)时，完全遗忘上一时刻的细胞状态。

遗忘门的计算公式：

\(f_t = \sigma(W_{xf}x_t + W_{hf}h_{t-1} + b_f)\)

其中，\(W_{xf}\)、\(W_{hf}\)为遗忘门的权重矩阵，\(b_f\)为偏置项。

1.2.3 输入门（Input Gate）

输入门由两部分组成：一是通过 sigmoid 激活函数输出的 "更新门"\(i_t\)，决定是否将新的信息存入细胞状态；二是通过\(\tanh\)激活函数生成的 "候选细胞状态"\(\tilde{c}_t\)，包含当前时刻的输入信息。

输入门的计算公式：

\(i_t = \sigma(W_{xi}x_t + W_{hi}h_{t-1} + b_i)\)

\(\tilde{c}t = \tanh(W{xc}x_t + W_{hc}h_{t-1} + b_c)\)

其中，\(W_{xi}\)、\(W_{hi}\)、\(W_{xc}\)、\(W_{hc}\)为输入门的权重矩阵，\(b_i\)、\(b_c\)为偏置项。

1.2.4 细胞状态更新

结合遗忘门和输入门的输出，LSTM 的细胞状态更新公式为：

\(c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t\)

这一公式的核心是 "选择性遗忘" 与 "选择性更新"：先通过遗忘门丢弃无关信息，再将当前时刻的重要信息（通过输入门筛选）加入细胞状态。

1.2.5 输出门（Output Gate）

输出门决定当前时刻的细胞状态中哪些信息会被输出到隐藏状态\(h_t\)。首先通过 sigmoid 激活函数生成输出门的控制信号\(o_t\)，然后将细胞状态\(c_t\)经过\(\tanh\)激活函数（将取值范围压缩到\([-1,1]\)）后，与\(o_t\)进行元素 - wise 乘法，得到当前时刻的隐藏状态\(h_t\)。

输出门的计算公式：

\(o_t = \sigma(W_{xo}x_t + W_{ho}h_{t-1} + b_o)\)

\(h_t = o_t \odot \tanh(c_t)\)

其中，\(W_{xo}\)、\(W_{ho}\)为输出门的权重矩阵，\(b_o\)为偏置项。

1.3 LSTM 的完整数学模型

综合以上门控机制，LSTM 的完整前向传播公式总结如下：

遗忘门：\(f_t = \sigma(W_{xf}x_t + W_{hf}h_{t-1} + b_f)\)

输入门更新信号：\(i_t = \sigma(W_{xi}x_t + W_{hi}h_{t-1} + b_i)\)

候选细胞状态：\(\tilde{c}t = \tanh(W{xc}x_t + W_{hc}h_{t-1} + b_c)\)

细胞状态更新：\(c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t\)

输出门：\(o_t = \sigma(W_{xo}x_t + W_{ho}h_{t-1} + b_o)\)

隐藏状态输出：\(h_t = o_t \odot \tanh(c_t)\)

最终输出（以分类任务为例）：\(y_t = \sigma(W_{hy}h_t + b_y)\)

1.4 LSTM 的梯度传播优势

LSTM 之所以能缓解梯度消失问题，核心在于细胞状态的加法更新机制。在反向传播过程中，细胞状态的梯度计算如下：

\(\frac{\partial Loss}{\partial c_t} = \frac{\partial Loss}{\partial h_t} \cdot o_t \cdot (1 - \tanh^2(c_t)) + \frac{\partial Loss}{\partial c_{t+1}} \cdot f_{t+1}\)

由于细胞状态的梯度是前一时刻梯度与当前时刻门控信号的加法运算，而非乘法运算，梯度不会因时间步增加而呈指数级衰减。即使对于长序列，梯度也能通过细胞状态有效传递到早期时间步，从而使模型能够学习到长期依赖关系。

二、LSTM 的代码实现：TensorFlow 与 PyTorch 双框架

2.1 环境准备

在开始代码实现前，需要安装以下依赖库：

复制代码

# 安装TensorFlow（GPU版本）

pip install tensorflow-gpu==2.10.0

# 安装PyTorch（GPU版本，根据CUDA版本调整）

pip install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu118

# 安装其他依赖库

pip install numpy pandas matplotlib scikit-learn

2.2 TensorFlow/Keras 实现 LSTM

Keras 是 TensorFlow 的高层 API，提供了简洁的 LSTM 接口，支持快速构建模型。以下将实现一个基础的 LSTM 模型，包含自定义 LSTM 层（手动实现门控机制）和使用 Keras 内置 LSTM 层两种方式。

2.2.1 自定义 LSTM 层（手动实现门控机制）

复制代码

import tensorflow as tf

from tensorflow.keras.layers import Layer

from tensorflow.keras.models import Model

from tensorflow.keras.layers import Input

class CustomLSTM(Layer):

def __init__(self, units, return_sequences=False, return_state=False, **kwargs):

super(CustomLSTM, self).__init__(**kwargs)

self.units = units # LSTM单元数量（隐藏层维度）

self.return_sequences = return_sequences # 是否返回所有时间步的输出

self.return_state = return_state # 是否返回细胞状态和隐藏状态

def build(self, input_shape):

input_dim = input_shape[-1] # 输入特征维度

# 定义权重矩阵（遗忘门、输入门、候选细胞状态、输出门）

self.Wf = self.add_weight(shape=(input_dim, self.units), initializer='glorot_uniform', name='Wf')

self.Wi = self.add_weight(shape=(input_dim, self.units), initializer='glorot_uniform', name='Wi')

self.Wc = self.add_weight(shape=(input_dim, self.units), initializer='glorot_uniform', name='Wc')

self.Wo = self.add_weight(shape=(input_dim, self.units), initializer='glorot_uniform', name='Wo')

self.Uf = self.add_weight(shape=(self.units, self.units), initializer='glorot_uniform', name='Uf')

self.Ui = self.add_weight(shape=(self.units, self.units), initializer='glorot_uniform', name='Ui')

self.Uc = self.add_weight(shape=(self.units, self.units), initializer='glorot_uniform', name='Uc')

self.Uo = self.add_weight(shape=(self.units, self.units), initializer='glorot_uniform', name='Uo')

# 定义偏置项

self.bf = self.add_weight(shape=(self.units,), initializer='zeros', name='bf')

self.bi = self.add_weight(shape=(self.units,), initializer='zeros', name='bi')

self.bc = self.add_weight(shape=(self.units,), initializer='zeros', name='bc')

self.bo = self.add_weight(shape=(self.units,), initializer='zeros', name='bo')

super(CustomLSTM, self).build(input_shape)

def call(self, inputs, initial_state=None):

# inputs形状：(batch_size, time_steps, input_dim)

batch_size, time_steps, input_dim = inputs.shape

# 初始化隐藏状态和细胞状态（若未提供初始状态）

if initial_state is None:

h0 = tf.zeros(shape=(batch_size, self.units), dtype=tf.float32)

c0 = tf.zeros(shape=(batch_size, self.units), dtype=tf.float32)

else:

h0, c0 = initial_state

h_t = h0

c_t = c0

outputs = []

# 遍历每个时间步

for t in range(time_steps):

x_t = inputs[:, t, :] # 当前时间步输入：(batch_size, input_dim)

# 1. 计算遗忘门

f_t = tf.sigmoid(tf.matmul(x_t, self.Wf) + tf.matmul(h_t, self.Uf) + self.bf)

# 2. 计算输入门和候选细胞状态

i_t = tf.sigmoid(tf.matmul(x_t, self.Wi) + tf.matmul(h_t, self.Ui) + self.bi)

c_tilde = tf.tanh(tf.matmul(x_t, self.Wc) + tf.matmul(h_t, self.Uc) + self.bc)

# 3. 更新细胞状态

c_t = f_t * c_t + i_t * c_tilde

# 4. 计算输出门和隐藏状态

o_t = tf.sigmoid(tf.matmul(x_t, self.Wo) + tf.matmul(h_t, self.Uo) + self.bo)

h_t = o_t * tf.tanh(c_t)

# 保存当前时间步的输出

outputs.append(h_t)

# 整理输出形状

outputs = tf.stack(outputs, axis=1) # (batch_size, time_steps, units)

if not self.return_sequences:

outputs = outputs[:, -1, :] # 仅返回最后一个时间步的输出：(batch_size, units)

# 返回结果（根据return_state参数决定是否返回状态）

if self.return_state:

return outputs, h_t, c_t

else:

return outputs

def compute_output_shape(self, input_shape):

if self.return_sequences:

return (input_shape[0], input_shape[1], self.units)

else:

return (input_shape[0], self.units)

# 测试自定义LSTM层

if __name__ == "__main__":

# 构建模型

input_layer = Input(shape=(10, 5)) # 输入：(batch_size, 10个时间步, 5个特征)

lstm_layer = CustomLSTM(units=32, return_sequences=False, return_state=False)

output_layer = lstm_layer(input_layer)

model = Model(inputs=input_layer, outputs=output_layer)

# 打印模型结构

model.summary()

# 测试前向传播

test_input = tf.random.normal(shape=(32, 10, 5)) # (batch_size=32, time_steps=10, input_dim=5)

test_output = model(test_input)

print("输出形状：", test_output.shape) # 输出：(32, 32)