《数据结构——排序（上）》从扑克牌到分治法：插入排序与希尔排序的深度剖析

目录

[1. 排序算法入门：为什么我们需要多种排序算法？](#1. 排序算法入门：为什么我们需要多种排序算法？)

评判排序算法的四大维度

[2. 直接插入排序：扑克牌整理的艺术](#2. 直接插入排序：扑克牌整理的艺术)

[2.1 基本思想](#2.1 基本思想)

2.2代码实现

[2.3 性能分析](#2.3 性能分析)

[2.4 适用场景](#2.4 适用场景)

[2.5 小提醒：边界条件的陷阱](#2.5 小提醒：边界条件的陷阱)

[2.6 LeetCode实战：链表插入排序](#2.6 LeetCode实战：链表插入排序)

[3. 希尔排序：插入排序的进化版](#3. 希尔排序：插入排序的进化版)

[3.1 基本思想](#3.1 基本思想)

[3.2 代码实现](#3.2 代码实现)

[3.3 gap序列选择](#3.3 gap序列选择)

[3.4 复杂度分析](#3.4 复杂度分析)

[3.5 个人调试经验：gap取值的陷阱](#3.5 个人调试经验：gap取值的陷阱)

[3.6 工程应用：Linux内核中的希尔排序](#3.6 工程应用：Linux内核中的希尔排序)

[4. 两种算法对比与适用场景](#4. 两种算法对比与适用场景)

[5. 思考题](#5. 思考题)

[6. 下期预告](#6. 下期预告)

排序算法系列上篇：本文将带大家从最基础的插入排序开始，逐步深入到希尔排序，通过扑克牌整理的直观类比，结合真实代码实现和调试经验，彻底掌握这两种排序算法的核心思想与工程应用。文末还有LeetCode实战题解析和STL底层原理彩蛋！

1. 排序算法入门：为什么我们需要多种排序算法？

在开始学习具体算法之前，让我们先思考一个问题：为什么计算机科学中需要这么多不同的排序算法？

在日常生活中，排序无处不在：

电商平台按价格/销量排序商品
学校按成绩排名学生
音乐APP按热度排序歌曲

每种场景对排序的要求不同：

数据规模：小到几十个学生排名，大到数亿条电商订单
性能要求：实时响应 vs 后台批量处理
内存限制：嵌入式设备 vs 服务器集群
稳定性需求：是否需要保持相同元素的相对顺序

评判排序算法的四大维度

时间复杂度：算法执行时间随数据规模的增长速率
空间复杂度：算法执行所需的额外内存空间
稳定性：相同元素排序后相对位置是否保持不变
适应性：对已部分有序数据的处理效率

面试高频考点 ：LeetCode 912. Sort an Array 是排序算法的经典面试题，要求实现一个能处理任意整数数组的排序函数。这道题看似简单，却能考察候选人对不同排序算法的理解和选择能力。

2. 直接插入排序：扑克牌整理的艺术

2.1 基本思想

直接插入排序就像我们整理扑克牌的过程：假设左手已经拿了一部分有序的牌，右手从牌堆中取出一张新牌，然后从右向左依次比较，找到合适的位置插入，使得左手的牌始终保持有序。

具体步骤：

从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后

2.2代码实现

复制代码

#include <iostream>
using namespace std;

// 直接插入排序
void InsertSort(int* a, int n) {
    for (int i = 0; i < n - 1; i++) {
        int end = i;           // 已排序序列的最后一个元素下标
        int tmp = a[end + 1];  // 待插入的元素
        
        // 从后向前比较，找到插入位置
        while (end >= 0) {
            if (a[end] > tmp) {
                // 元素后移
                a[end + 1] = a[end];
                end--;
            } else {
                break;  // 找到插入位置
            }
        }
        // 插入元素
        a[end + 1] = tmp;
    }
}

// 打印数组
void PrintArray(int* a, int n) {
    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }
    cout << endl;
}

int main() {
    int a[] = {5, 3, 9, 6, 2, 4, 7, 1, 8};
    int n = sizeof(a) / sizeof(a[0]);
    
    cout << "排序前: ";
    PrintArray(a, n);
    
    InsertSort(a, n);
    
    cout << "排序后: ";
    PrintArray(a, n);
    
    return 0;
}

2.3 性能分析

时间复杂度 ：O(N²)
- 最好情况（已经有序）：O(N)，只需比较N-1次
- 最坏情况（完全逆序）：O(N²)，每次插入都需要移动所有已排序元素
- 平均情况：O(N²)
空间复杂度：O(1)，只需要一个临时变量
稳定性 ：稳定，相同元素不会改变相对顺序

2.4 适用场景

直接插入排序在以下场景表现优异：

小规模数据：当n较小时（如n<10），插入排序的常数因子较小
近乎有序的数据：当数组大部分已经有序时，效率接近O(N)
在线排序：数据是逐步到达的，需要动态维护有序性

2.5 小提醒：边界条件的陷阱

上数据结构课时，我第一次实现插入排序遇到了一个经典bug。当时的代码是这样的：

复制代码

void buggyInsertSort(int* a, int n) {
    for (int i = 1; i < n; i++) {
        int key = a[i];
        int j = i - 1;
        while (j >= 0 && a[j] > key) {
            a[j + 1] = a[j];
            j--;
        }
        a[j] = key; // 错误！应该是a[j+1] = key;
    }
}

测试用例{5, 2, 4, 6, 1, 3}排序后变成了{2, 2, 4, 5, 1, 3}，明显有问题。我在实验室debug了整整一个晚上，最后发现当j--后变成-1时，a[j] = key会导致数组越界访问。

小经验 ：在算法实现中，边界条件 是最容易出错的地方。建议在循环结束时添加打印语句，帮助定位问题。例如：cout << "Current index: " << j << endl; 这个教训让我在之后的编程中格外注意边界条件。

2.6 LeetCode实战：链表插入排序

LeetCode 147. Insertion Sort List 要求对单链表进行插入排序。这道题比数组更复杂，因为链表不能随机访问，需要维护多个指针。

复制代码

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

ListNode* insertionSortList(ListNode* head) {
    if (!head || !head->next) return head;
    
    ListNode* dummy = new ListNode(0); // 哑节点，简化边界处理
    ListNode* curr = head;
    
    while (curr) {
        // 保存下一个节点
        ListNode* next = curr->next;
        
        // 在已排序部分找到插入位置
        ListNode* prev = dummy;
        while (prev->next && prev->next->val < curr->val) {
            prev = prev->next;
        }
        
        // 插入当前节点
        curr->next = prev->next;
        prev->next = curr;
        
        // 移动到下一个节点
        curr = next;
    }
    
    return dummy->next;
}

解题思路：

创建一个哑节点(dummy node)简化边界处理
遍历原始链表，对每个节点在已排序部分找到合适位置
将当前节点插入到已排序部分
时间复杂度O(N²)，空间复杂度O(1)

面试技巧：当面试官问到链表排序时，除了插入排序，还可以讨论归并排序（时间复杂度O(NlogN)）等更优方案，展示你的算法知识广度。

3. 希尔排序：插入排序的进化版

3.1 基本思想

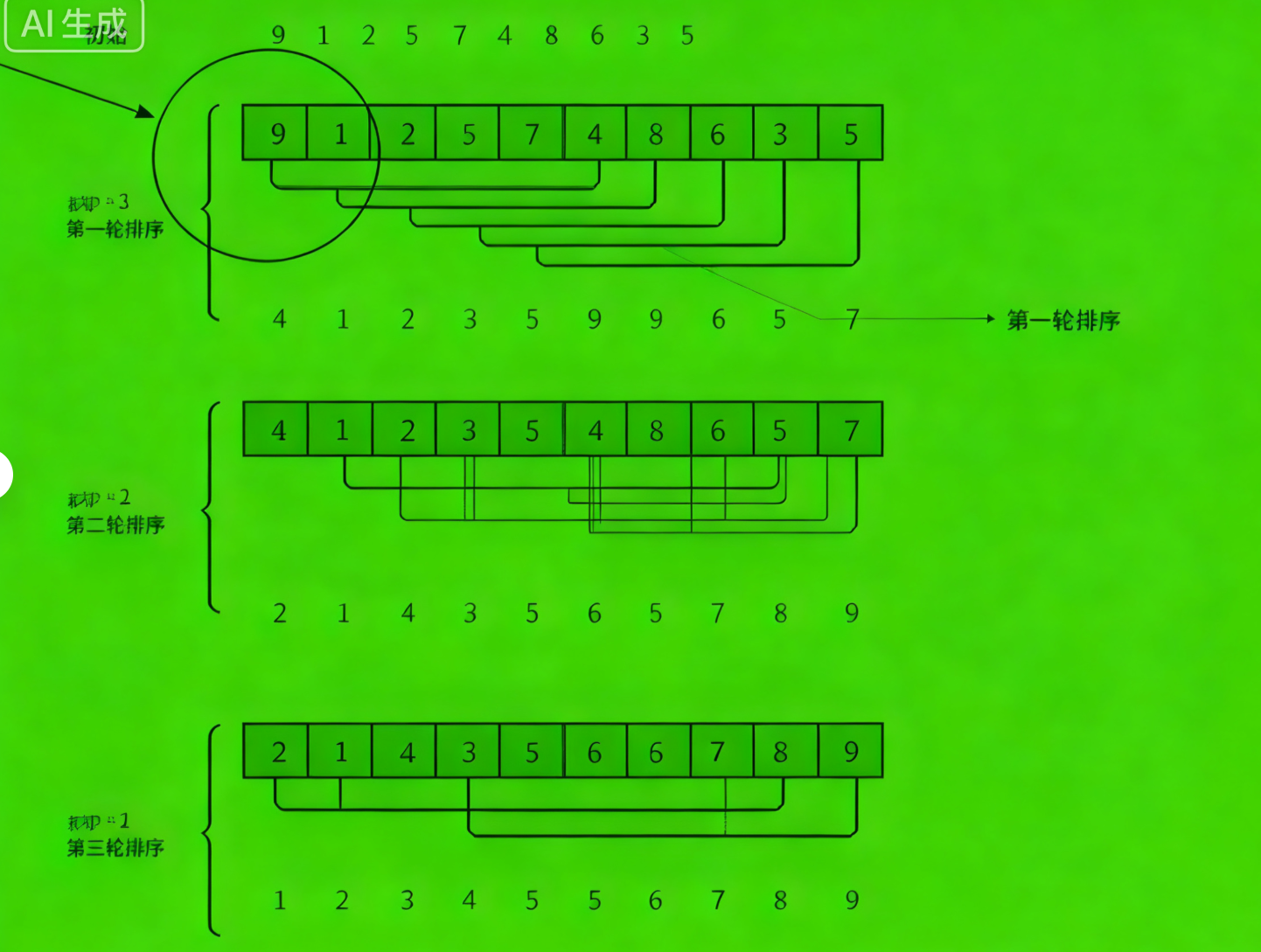
希尔排序 （Shell Sort）是直接插入排序的改进版，由Donald Shell在1959年提出。它的核心思想是：先将整个待排序序列分割成若干子序列，分别进行直接插入排序，当整个序列基本有序时，再对全体元素进行一次直接插入排序。

这种"分而治之"的策略大大提高了排序效率。希尔排序的关键在于gap序列的选择：

初始时gap较大，进行粗略排序
逐步减小gap，使序列越来越有序
最后当gap=1时，进行精细排序（即直接插入排序）

3.2 代码实现

复制代码

#include <iostream>
using namespace std;

// 希尔排序
void ShellSort(int* a, int n) {
    int gap = n;
    while (gap > 1) {
        // 推荐写法：除3
        gap = gap / 3 + 1;
        
        // 对每个分组进行插入排序
        for (int i = 0; i < n - gap; i++) {
            int end = i;
            int tmp = a[end + gap];
            
            // 组内插入排序
            while (end >= 0) {
                if (a[end] > tmp) {
                    a[end + gap] = a[end];
                    end -= gap;
                } else {
                    break;
                }
            }
            a[end + gap] = tmp;
        }
    }
}

// 打印数组
void PrintArray(int* a, int n) {
    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }
    cout << endl;
}

int main() {
    int a[] = {5, 3, 9, 6, 2, 4, 7, 1, 8};
    int n = sizeof(a) / sizeof(a[0]);
    
    cout << "排序前: ";
    PrintArray(a, n);
    
    ShellSort(a, n);
    
    cout << "排序后: ";
    PrintArray(a, n);
    
    return 0;
}

3.3 gap序列选择

gap序列的选择对希尔排序的性能影响很大。常见的gap序列有：

Shell序列：n/2, n/4, n/8, ..., 1
Knuth序列：(3^k-1)/2，如1, 4, 13, 40, ...
Hibbard序列：2^k-1，如1, 3, 7, 15, ...
Sedgewick序列：更复杂的数学公式

PDF中推荐的gap = gap/3 + 1是一种实践中表现不错的序列，能够达到O(n^1.3)的时间复杂度。

3.4 复杂度分析

希尔排序的时间复杂度估算：

外层循环：外层循环的时间复杂度可以直接给出为：O(log2 n) 或者O(log3 n) ，即O(log n)

内层循环：

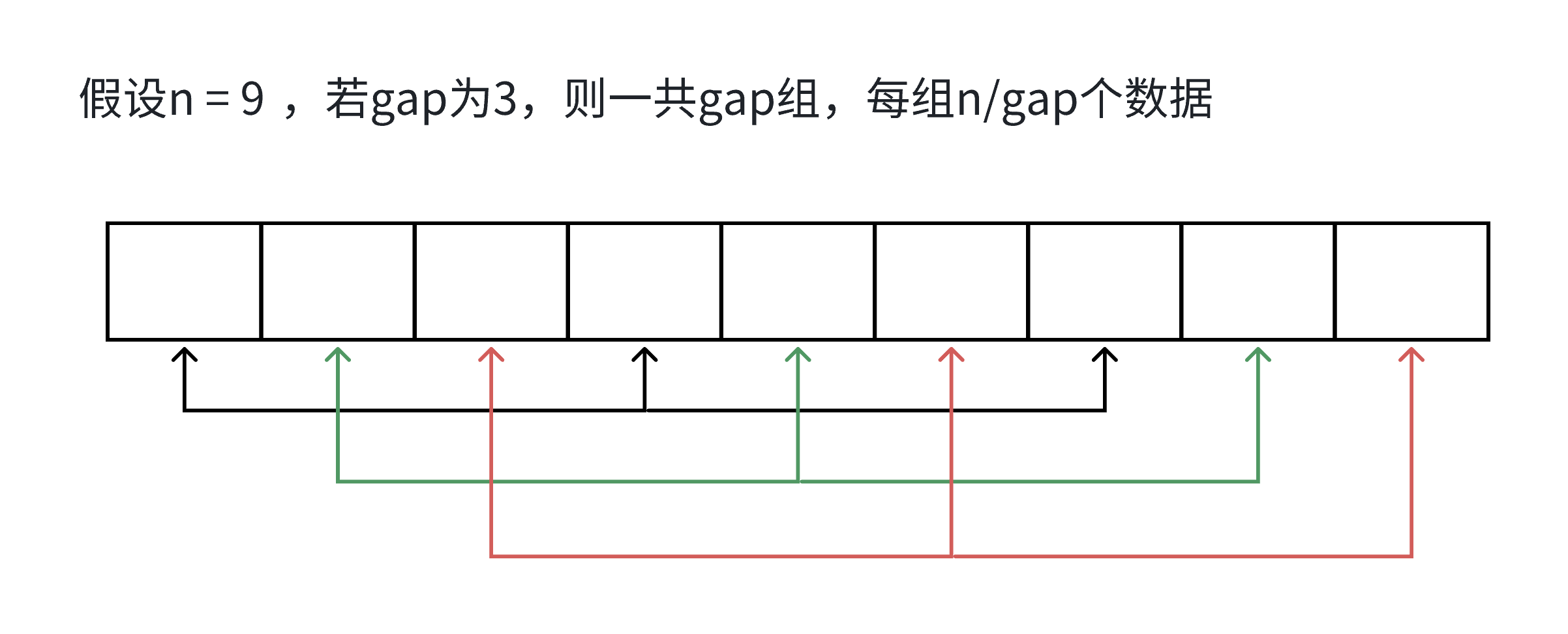
假设⼀共有n个数据，合计gap组，则每组为n/gap个；

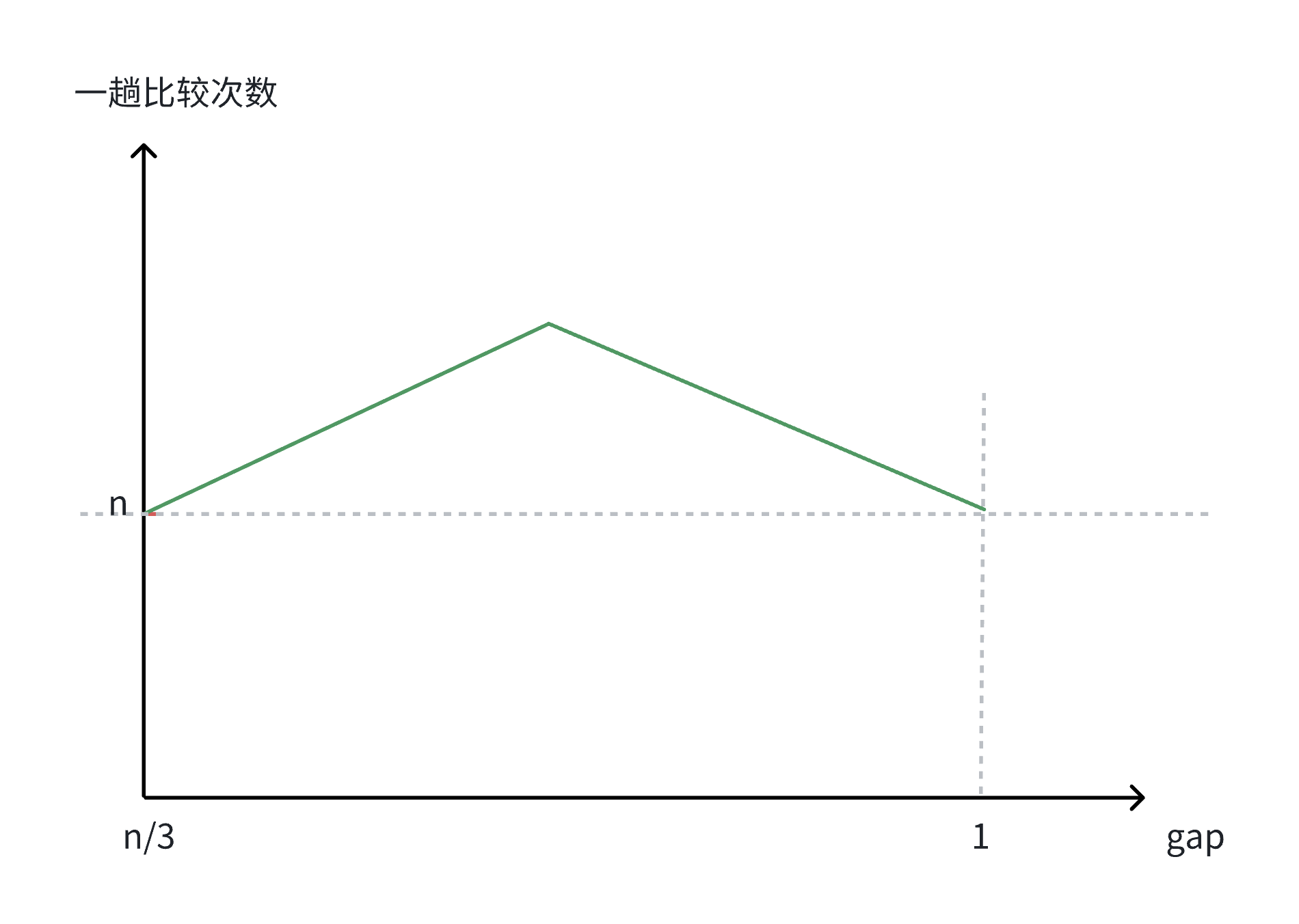
因此，希尔排序在最初和最后的排序的次数都为n，即前⼀阶段排序次数是逐渐上升的状态，当到达某⼀顶点时，排序次数逐渐下降⾄n，⽽该顶点的计算暂时⽆法给出具体的计算过程

因此

时间复杂度 ：取决于gap序列
- 最坏情况：O(N²)（使用不良的gap序列）
- 平均情况：O(N^1.3)（使用推荐的gap序列）
- 最好情况：O(N)（已经基本有序）
空间复杂度：O(1)，原地排序
稳定性 ：不稳定，因为相同元素可能被分到不同组中，相对顺序可能改变

3.5 个人调试经验：gap取值的陷阱

在一次算法作业中，我使用了以下gap序列实现：

复制代码

void wrongShellSort(int* a, int n) {
    int gap = n / 2;  // 错误的gap序列
    while (gap > 0) {
        for (int i = gap; i < n; i++) {
            int temp = a[i];
            int j = i;
            while (j >= gap && a[j - gap] > temp) {
                a[j] = a[j - gap];
                j -= gap;
            }
            a[j] = temp;
        }
        gap /= 2;  // 可能导致死循环
    }
}

测试用例{1, 2, 3, 4, 5}时一切正常，但当输入{5, 4, 3, 2, 1}时，程序竟然卡死了！通过打印gap值，我发现当n=5时，gap序列为2, 1, 0, 0, 0...，而循环条件gap > 0在gap=0时应该退出，但因为整数除法，gap始终为0，导致死循环。

调试心得 ：希尔排序的gap序列设计需要非常谨慎。推荐使用gap = gap/3 + 1 ，它能保证gap最终会变成1，避免死循环。另外，在循环中添加打印语句cout << "Current gap: " << gap << endl;能帮助快速定位问题。

3.6 工程应用：Linux内核中的希尔排序

有趣的是，希尔排序在Linux内核中也有应用。在/kernel/sched/core.c文件中，调度器使用希尔排序对运行队列进行排序，因为：

代码简单，易于维护
对于小规模数据（通常调度队列不会太大），性能足够好
原地排序，不需要额外内存

这证明了即使是"古老"的算法，在特定场景下仍有其价值。

4. 两种算法对比与适用场景

选择建议：

数据量小于10：直接插入排序
数据量10~10000，且内存受限：希尔排序
需要稳定排序：避免希尔排序，考虑归并排序

5. 思考题

为什么希尔排序在gap=1时效率会很高？
如果将希尔排序的gap序列改为2的幂次方（n/2, n/4, n/8...），会对性能产生什么影响？

答案放在评论区喽

6. 下期预告

中篇将深入探讨选择排序家族（直接选择、堆排序）为什么堆排序升序要建大堆？冒泡排序有哪些优化技巧？

下期亮点：通过一个LeetCode 215. Kth Largest Element in an Array的真实案例，展示堆排序在解决Top K问题时的强大优势，以及如何在面试中优雅地实现它！

系列导航：

$上篇\] 本篇：插入排序与希尔排序$
$下篇\] 终章：[快速排序、归并排序与非比较排序 + 全面性能对比](https://blog.csdn.net/dongaoran/article/details/155492909?fromshare=blogdetail&sharetype=blogdetail&sharerId=155492909&sharerefer=PC&sharesource=dongaoran&sharefrom=from_link "快速排序、归并排序与非比较排序 + 全面性能对比")$