二叉平衡树 - 技术栈

AVL树

向二叉树插入新节点后，如果能保证每个结点的左右子树高度差的绝对值不超过1，那么这棵树就是AVL树，具有以下性质

1.左右子树都是AVL树

2.左右两树高度之差（平衡因子）的绝对值不超过1(-1/0/1)

节点的定义

AVL树节点需定义左右节点，父节点，val值以及平衡因子

java 复制代码

   static class TreeNode{
        TreeNode left=null;
        TreeNode right=null;
        TreeNode parent=null;
        int val;
        int bf=0;

        public TreeNode(int val) {
            this.val = val;
        }
    }

AVL树的插入

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树的插入可以分成两步

1.按照搜索树的方式插入节点，

2.调节节点的平衡因子

插入节点

如果是空树，那么直接插入

java 复制代码

TreeNode node=new TreeNode(val);
        if(root==null){
            root=node;
            return true;
        }

如果不是空树，则按照查找逻辑确定插入位置

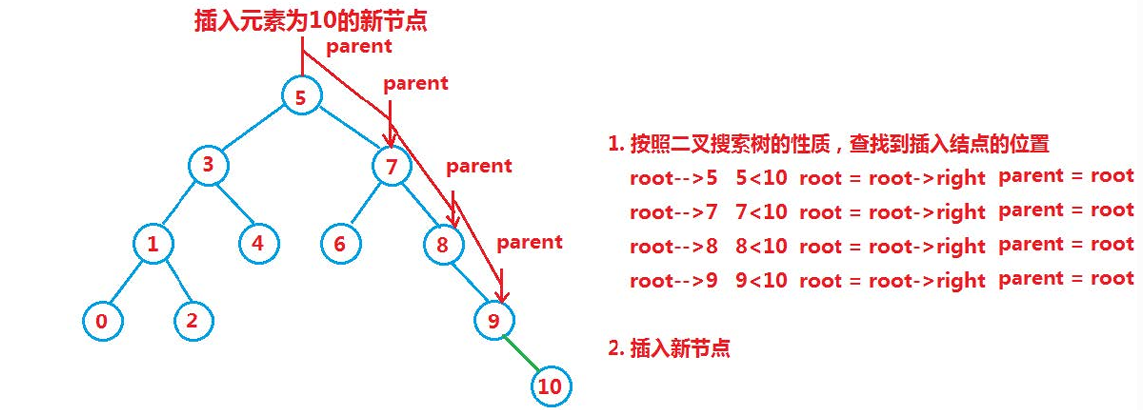
找到要插入的位置

java 复制代码

        TreeNode cur=root;
        TreeNode parent=root;
        while(cur!=null){
            if(cur.val>val){
                parent=cur;
                cur=cur.left;
            }else if(cur.val<val){
                parent=cur;
                cur=cur.right;
            }else{
                return false;
            }
        }

插入节点

java 复制代码

        if(parent.val>val){
            parent.left=node;
            parent.bf--;
        }else{
            parent.right=node;
            parent.bf++;
        }
        node.parent=parent;
        cur=node;

更新平衡因子

更新parent的平衡因子

因为要从下往上依次更新平衡因子，所以首先确定这是一个循环，先不管循环条件

当node插入到parent的右边时，bf++

当node插入到parent的左边时，bf--

java 复制代码

            if(parent.right==cur){
                parent.bf++;
            }else{
                parent.bf--;
            }

判断

当parent.bf==0 时，证明这棵树已经平衡，因为插入之前树就是平衡的，所以不需要继续向上调整

当parent.bf==1 || parent.bf==-1 时，证明parent不平衡，还需要继续向上更新

java 复制代码

            if(parent.bf==0){
                break;
            }else if(parent.bf==1||parent.bf==-1){
                cur=parent;
                parent=cur.parent;
            }

如果以上两种情况都不符合，那么只剩最后一种情况，那就是parent.bf==2 || parent.bf==-2 此时就需要对这棵树进行旋转，旋转后这棵树可以达到平衡，此时跳出循环

此时分为四种情况，分别是parent.bf等于2/-2、cur.bf等于1/-1

AVL树的旋转

往哪旋哪变高，相反的方向变低

右单旋

parent.bf == -2 && cur.bf ==-1

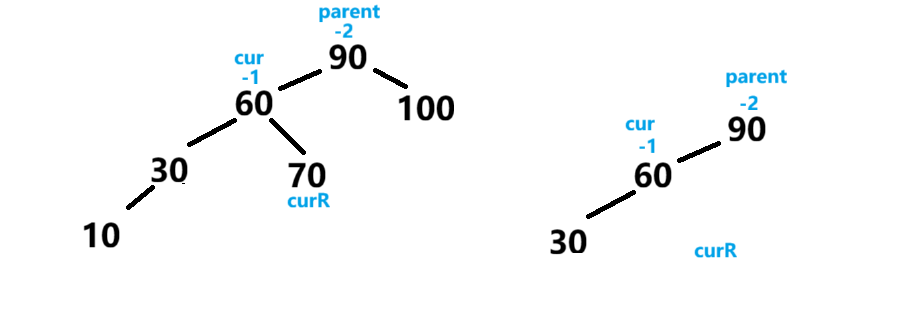
此时节点90 是失衡节点 bf==-2 说明左子树偏高 ，此时让parent的左子树成为树顶，parent成为其右子树 并将原本的右子树连接到parent的左子树，这时这棵树就回归平衡了。

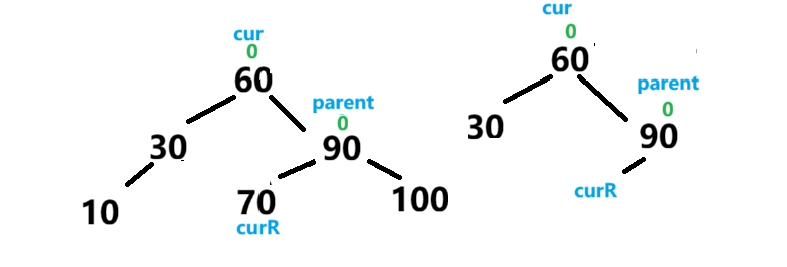
从节点的角度来说，右旋就是将parent节点 移到cur(parent左子树)的右子树 ，并将cur右边原来的节点 挂到parent的左子树 。然后将parent和cur的平衡因子更新为0

java 复制代码

private static void rotateRight(TreeNode parent) {
        TreeNode Pparent=parent.parent;
        TreeNode cur=parent.left;
        TreeNode curR=cur.right;
        parent.left=curR;
        cur.left=parent;
        if(parent==root){
            root=cur;
            cur.parent=null;
        }else{
            if(Pparent.left==parent){
                Pparent.left=cur;
                cur.parent=Pparent;
            }else{
                Pparent.right=cur;
                cur.parent=Pparent;
            }
        }
        parent.parent=cur;
        if(curR!=null) curR.parent=parent;
        parent.bf=0;
        cur.bf=0;
    }

左单旋

parent.bf==2 && cur.bf == 1

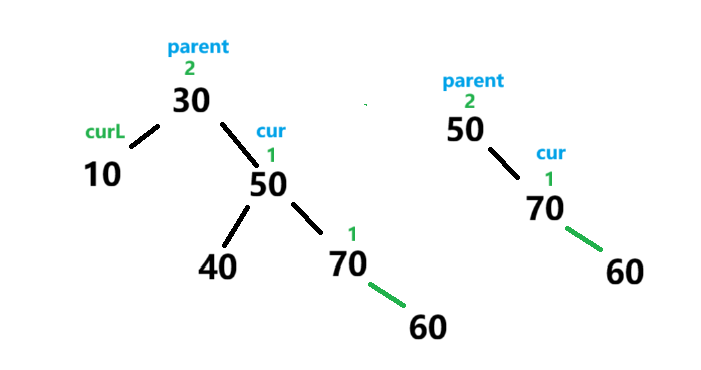
此时失衡节点是parent bf==2 说明右子树偏高 ，此时就是需要cur成为树顶 ，然后将parent变成其左子树 并将原本的左子树变成parent的右子树

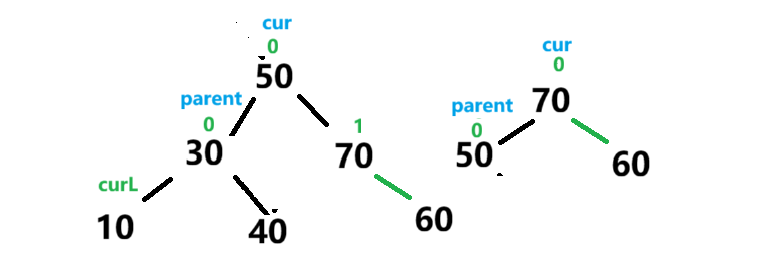
从节点的角度来说，左单旋就是将parent移到cur节点(parent右子树)的左子树上 ，并将左子树上原来的节点挂到parent的右子树 ，然后将cur和parent的平衡因子更新为0

java 复制代码

    private  void rotateLeft(TreeNode parent){
        TreeNode cur=parent.right;
        TreeNode curL=cur.left;
        TreeNode Pparent=parent.parent;
        if(parent==root){
            root=cur;
            cur.parent=null;
        }else{
            if(parent==Pparent.left){
                Pparent.left=cur;
            }else {
                Pparent.right = cur;
            }
            cur.parent=Pparent;
        }
       if(curL!=null) curL.parent=parent;
       parent.right=curL;
       cur.left=parent;
       parent.parent=cur;
       cur.bf=0;
       parent.bf=0;
    }

左右双旋

parent.bf == -2 && cur.bf ==1

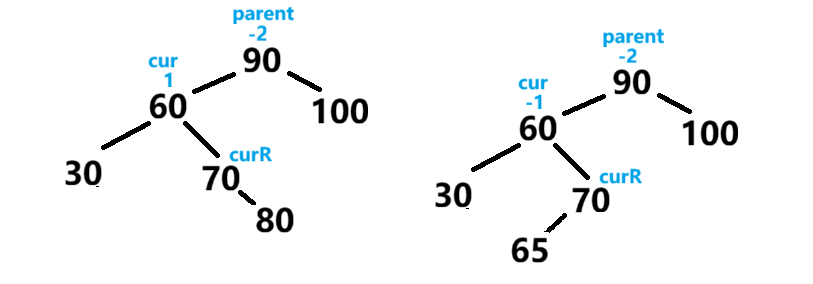
此时parent的左子树高 但是cur的右子树高 (但bf小于2)，那么就需要先将cur这棵树左旋，使其左子树变高，与parent情况统一

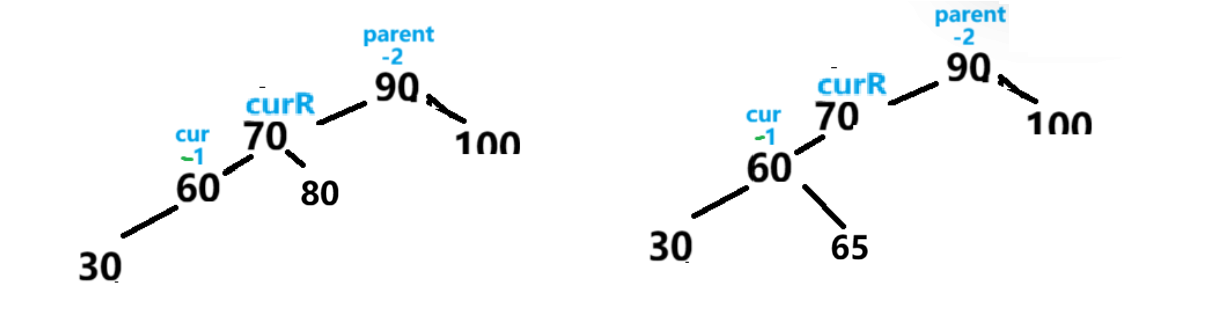
此时统一都是左子树高 ，那么调整parent右旋

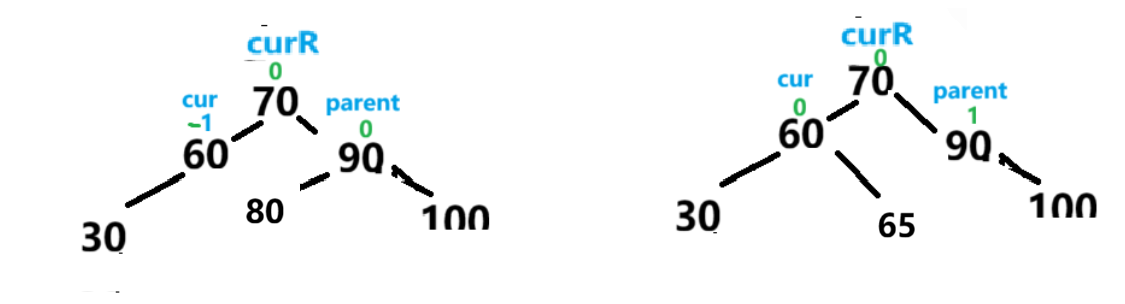
此时开始更新平衡因子

通过图可以发现，当curR.bf==1 时调整后cur.bf=-1其余为0

当curR.bf==-1 时调整后parent.bf=1其余为0

java 复制代码

                        rotateLeft(parent.left);
                        rotateRight(parent);
                        if(cur.right.bf==-1){
                            cur.bf=0;
                            cur.right.bf=0;
                            parent.bf=1;
                        }else{
                            cur.bf=-1;
                            cur.right.bf=0;
                            parent.bf=0;
                        }

右左双旋

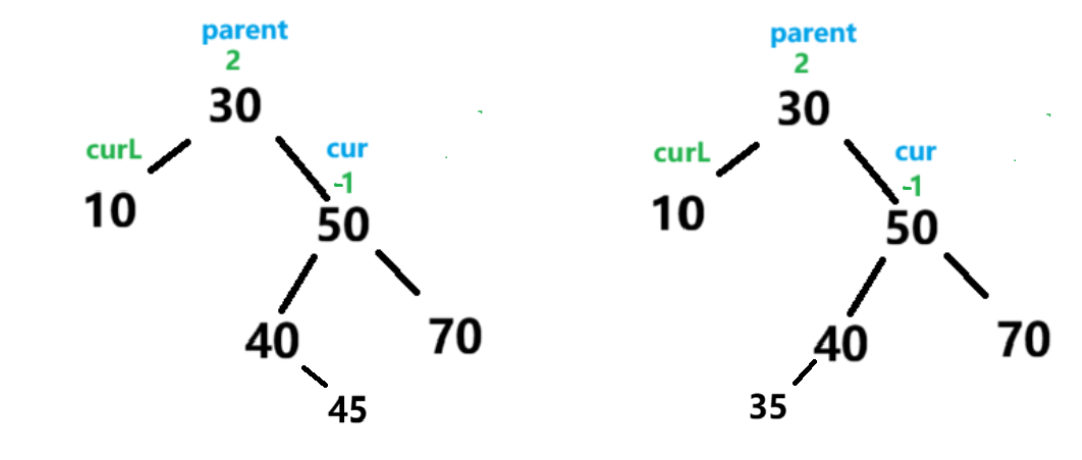
此时parent右子树高 ，cur左子树高 ，那么先将cur 右旋 ，使其右子树变高，与parent一致

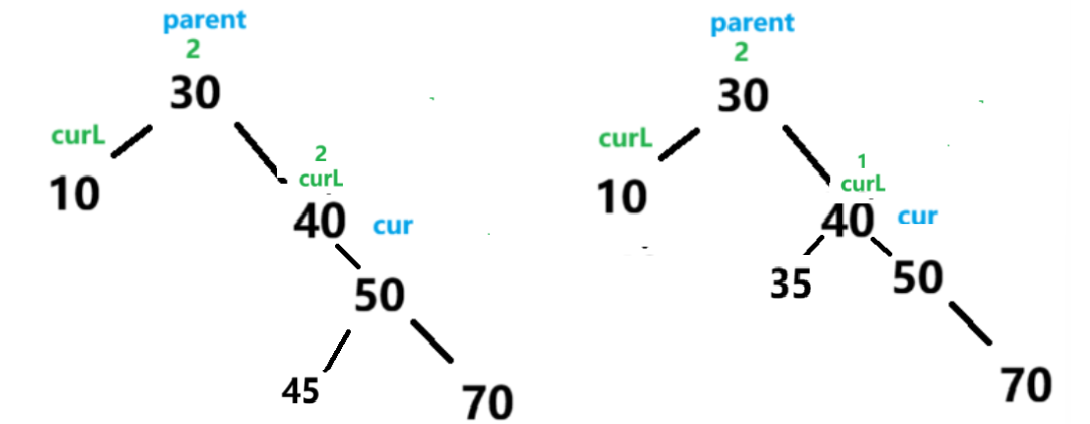
此时统一都是右子树高 ，那么对parent进行左旋

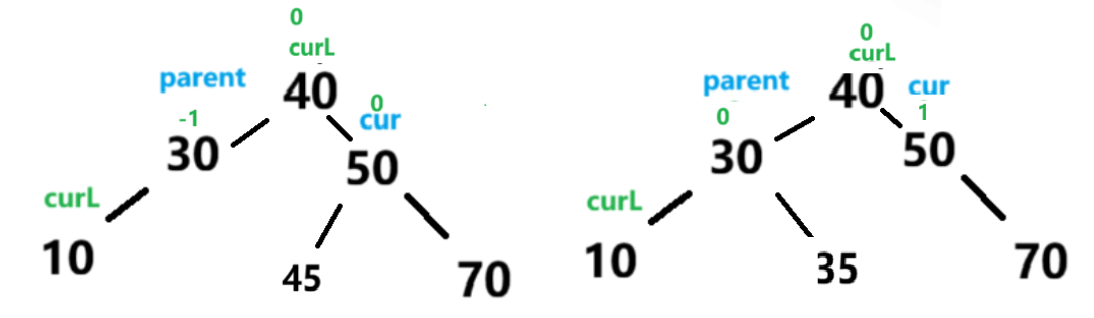
此时更新平衡因子：当curL.bf==1 时，parent.bf更新为-1其余更新为0

当curL.bf==-1 时，cur.bf更新为1其余更新为0

java 复制代码

                        rotateRight(parent.right);
                        rotateLeft(parent);
                        if(cur.left.bf==1){
                            parent.bf=-1;
                            cur.bf=0;
                            cur.left.bf=0;
                        }else{
                            parent.bf=0;
                            cur.bf=1;
                            cur.left.bf=0;
                        }

AVL树的验证

第一步： 中序遍历，若遍历结果为有序，说明是二叉搜索树

java 复制代码

    public void inorder(TreeNode root) {
        if (root == null) return;
        inorder(root.left);
        System.out.print(root.val + " ");
        inorder(root.right);
    }

第二步： 遍历每一个节点，计算其平衡因子判断是否小于2 ，并验证平衡因子的正确性

java 复制代码

    private int Height(TreeNode node){
        if(node==null) return 0;
        int left=Height(node.left);
        int right=Height(node.right);
        return Math.max(left,right)+1;
    }
    public boolean isBalance(TreeNode node){
        if(node==null) return true;
        int leftH=Height(node.left);
        int rightH=Height(node.right);
        if((rightH-leftH)!=node.bf){
            System.out.println("平衡因子异常");
        }
        return (Math.abs(leftH-rightH)<=1)
                &&isBalance(node.left)&&isBalance(node.right);

ALV树的删除

首先按照二叉搜索树的删除原则进行节点的删除

设待删除的节点为cur

1.cur.left==null

1）cur==root : root=cur.right

2）cur!=root : parent.right/left=cur.right

java 复制代码

        if(node.left==null){
            if(node==root){
                root=node.right;
                if(node.right!=null) node.right.parent=null;
            }else{
                if(node==node.parent.left){
                    node.parent.left=node.right;
                }else{
                    node.parent.right=node.right;
                }
                if(node.right!=null) node.right.parent=node.parent;
            }
        }

2.cur.right==null

1）cur==root : root=cur.left

2）cur!=root : parent.right/left=cur.left

java 复制代码

if(node.right==null){
            if(node==root){
                root=node.left;
                node.left.parent=null;
            }else{
                if(node==node.parent.left){
                    node.parent.left=node.left;
                }else{
                    node.parent.right=node.left;
                }
                node.left.parent=node.parent;
            }
        }

3**.cur.left==null && cur.right==null**

用替换法 进行删除，用cur**左子树的最大值（最右边）或者左子树的最小值（最左边）**进行替换

java 复制代码

    node.val=setNode(node);
  private int setNode(TreeNode node){
        TreeNode parent=node.right;
        TreeNode cur=parent.left;
        if(cur==null){
            node.right=parent.right;
            if(parent.right!=null) parent.right.parent=node;
            return parent.val;
        }
        while(cur!=null){
            parent=cur;
            cur=cur.left;
        }
        parent.parent.left=parent.right;
        if(parent.right!=null) parent.right.parent=parent.parent;
        return parent.val;
    }

现在开始更新平衡因子

从被删除节点的父节点，向上开始更新平衡因子，需要重新计算

性能分析

AVL树是绝对平衡的二叉树，查找的时间复杂度始终为O(logN)，但是插入数据时，会进行大量的旋转操作，性能较低，所以需要进行频繁插入删除数据时，不建议使用AVL树

红黑树

红黑树，是一种二叉搜索树 ，在每个节点上增加一个存储位，表示节点的颜色 ，可以是Red或者Black 。通过对任何一条从根到叶子的路径上各个节点的着色方法的限制，红黑树确保没有一条路径会比其他路径长出两倍，因此是接近平衡的

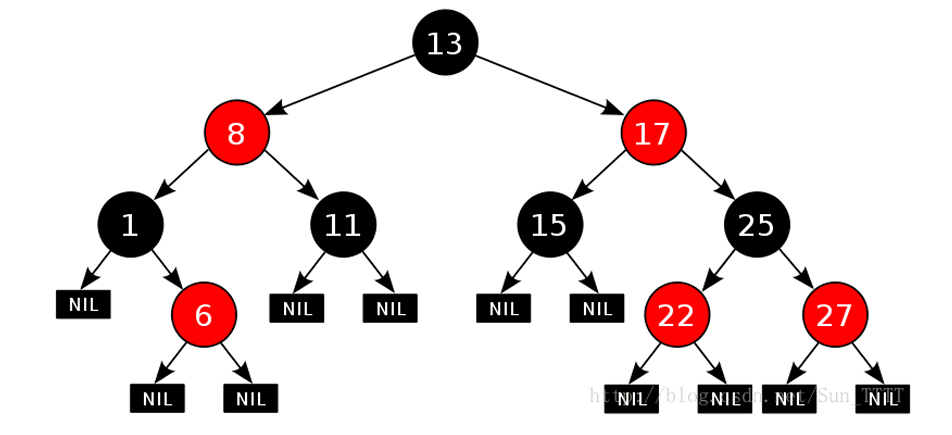
红黑树的性质

根节点是黑色的 ，黑色的子节点可以是黑色，也可以是红色。红色的子节点必须是黑色 。对于每个节点，从该节点到其所有后代 的简单路径上，黑色节点数是相等的 ，且最长路径最多是最短路径的两倍。每个是空节点 的叶节点(NIL) 都是黑色的

极端情况：

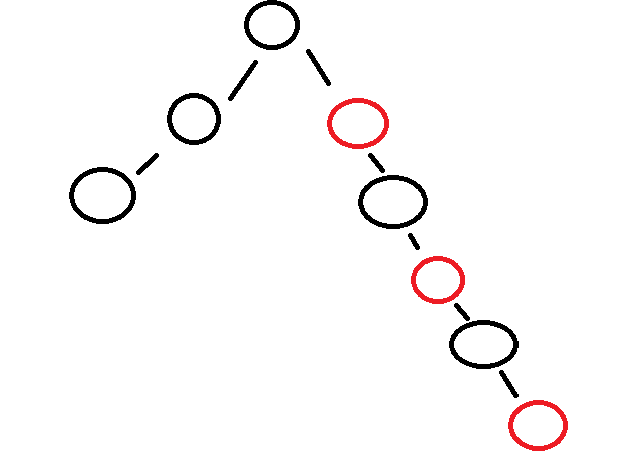
仍满足最长路径最多是最短路径的两倍

如果一颗红黑树有X个黑色节点 ，那么总节点数最多是2X ,最少是X。从而可以推导出:

当节点数是X 时，层数是logX ,时间复杂度就是O(logX)

当节点数是2X 时，层数是log2X ，时间复杂度是**(logX+1)** ，用大O渐进法就是O(logX)

根据N~2X ，可以推导出红黑树的时间复杂度就是O(logN)

节点的定义

节点的默认值必须是红色的，如果是黑色的，那么新加入节点的时候，就有可能需要新增节点来满足每条路径上黑色节点数目相同。如果是红色的，那么我们只需向上遍历来修改节点的颜色

使用枚举类型来定义颜色

java 复制代码

public class RBTree {
    static class RBTreeNode{
        public RBTreeNode left;
        public RBTreeNode right;
        public RBTreeNode parent;
        int val;
        COLOR color;

        public RBTreeNode(int val) {
            this.val = val;
            this.color = RED;
        }
    }

红黑树的插入

插入节点

这里的插入节点和AVL树/二叉平衡树相同

java 复制代码

 RBTreeNode node=new RBTreeNode(val);
        RBTreeNode parent=root;
        RBTreeNode cur=root;
        if(root==null){
            root=node;
            node.color= BLACK;
        }else{
            while(cur!=null){
                if(cur.val>val){
                    parent=cur;
                    cur=cur.left;
                }else if(cur.val<val){
                    parent=cur;
                    cur=cur.right;
                }else{
                    return false;
                }
            }
            if(val>parent.val){
                parent.right=node;
            }else{
                parent.left=node;
            }
            node.parent=parent;
        }

更新颜色

定义cur为当前节点

parent 为cur的父节点

uncle 为parent的兄弟节点

grandparend 为parent和uncle的父节点

首先先确定这是一个循环，不难发现当parent为黑色的时候 ，不需要额外更改颜色，所以循环条件就是parent存在且为红节点。

分为这六种情况

parent == grandparent.left

uncle为红色

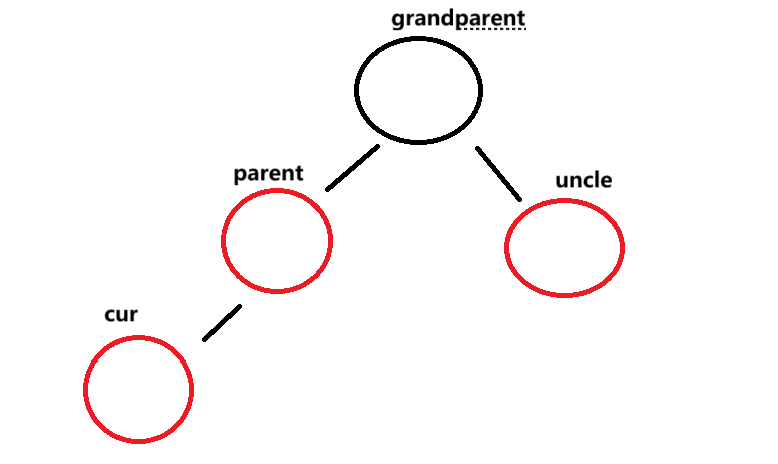
这里cur和parent两个红节点挨在了一起，所以要将parent和uncle变为黑色 ，将grandparent变为红色 。更新cur 指向grandparent，parent指向cur.parent

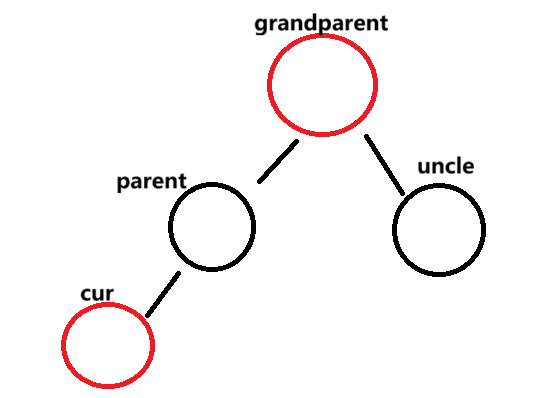
java 复制代码

                if(uncle!=null&&uncle.color==RED){
                    parent.color=BLACK;
                    uncle.color=BLACK;
                    grandparent.color=RED;
                    cur=grandparent;
                    parent=cur.parent;
                }

情况二

这里需要进行旋转，方式和AVL树一样，分为左单旋和右单旋

uncle为空或者为黑节点

cur == parent.left

此时要将grandparent右单旋

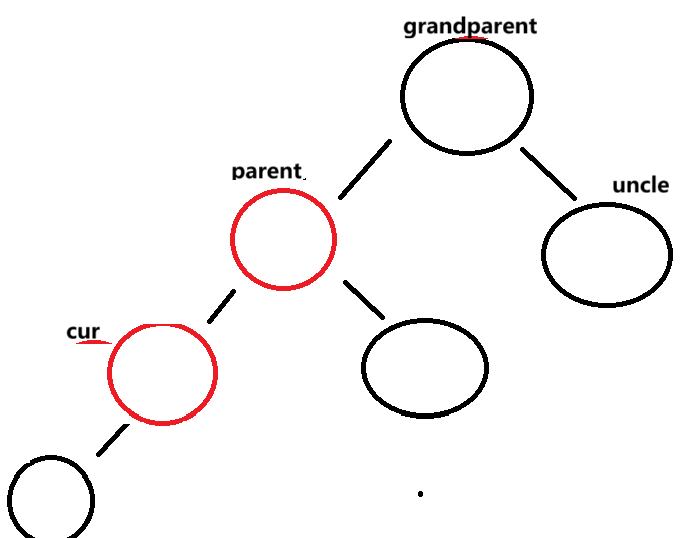
旋转后：

并将parent变为黑节点 ，grandparent变为红节点

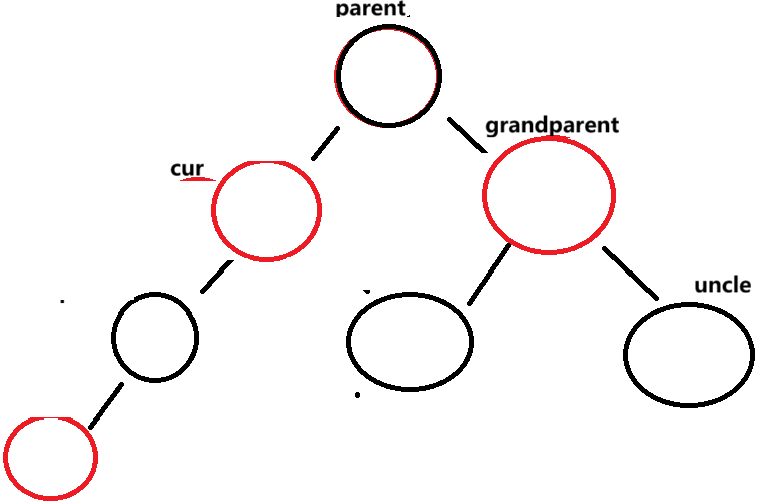
最后更新cur指向grandparent ，parent指向cur.parent

java 复制代码

                        rotateRight(grandparent);
                        parent.color=BLACK;
                        grandparent.color=RED;
                        cur=parent;
                        parent=cur.parent;

cur == parent.right

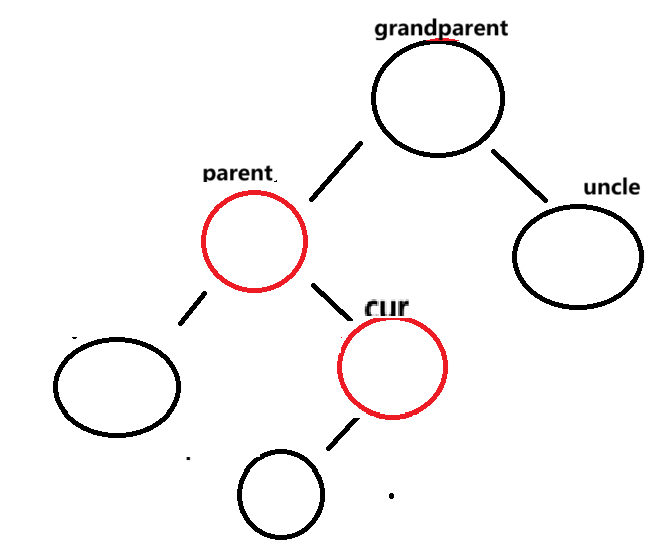
首先对parent进行左单旋 ，然后更新cur和parent

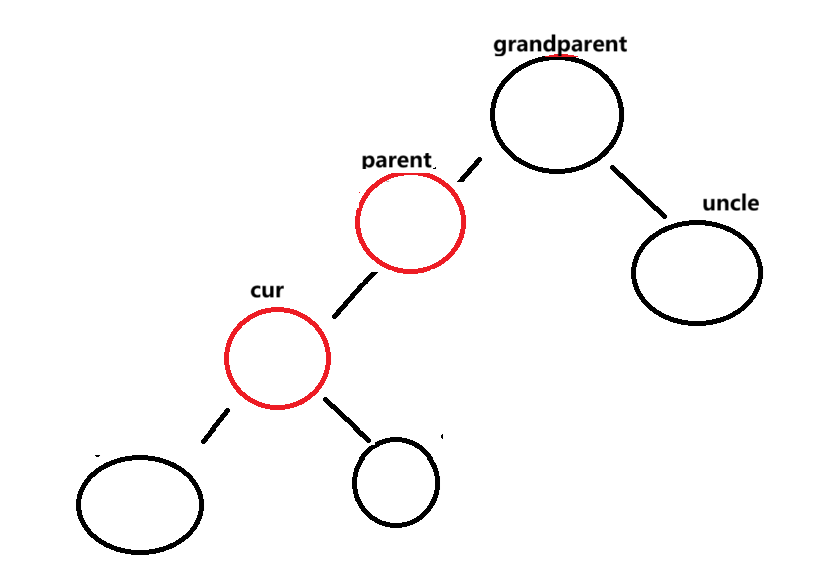
这时就变成了cur == parent.left这种情况，按照上一种方式旋转grandparent即可

java 复制代码

                    if (cur == parent.right) {
                        rotateLeft(parent);
                        parent=cur;
                        cur=parent.left;
                    }
                    rotateRight(grandparent);
                    parent.color=BLACK;
                    grandparent.color=RED;
                    cur=parent;
                    parent=cur.parent;

parent == grandparent.right

uncle存在且为红色

转换方式与parent == grandparent.left相同

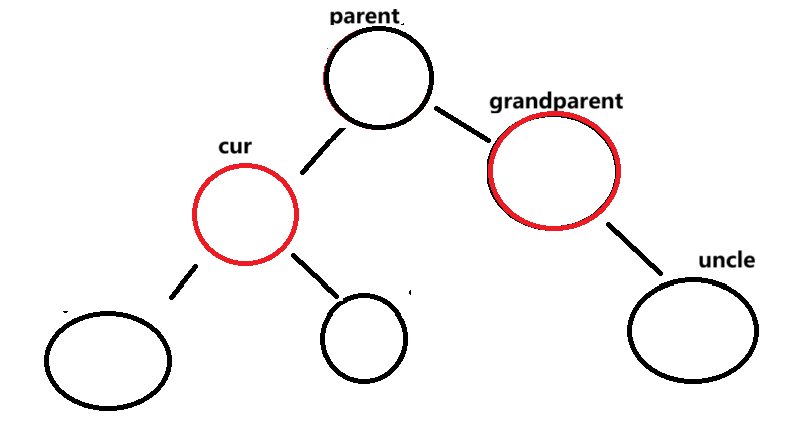
cur == parent.right

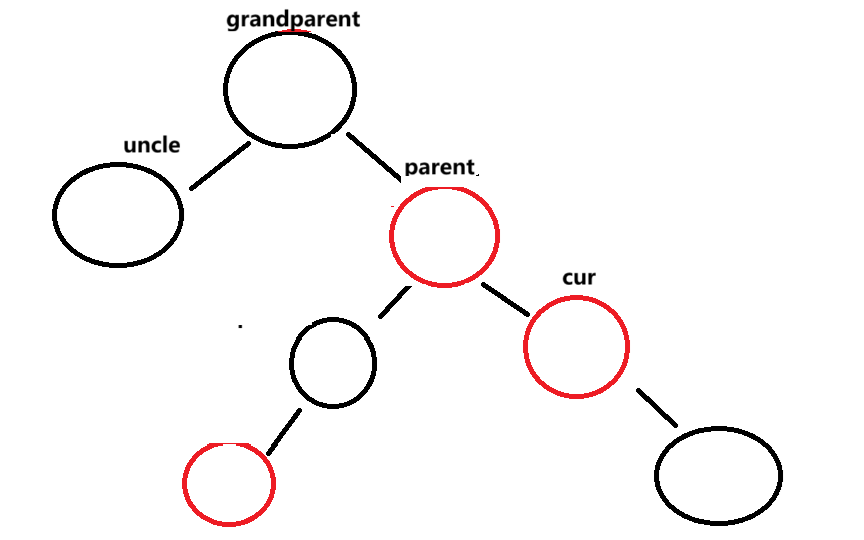
此时左旋grandparent 旋转后将parent置为黑色 grandparent置为红色

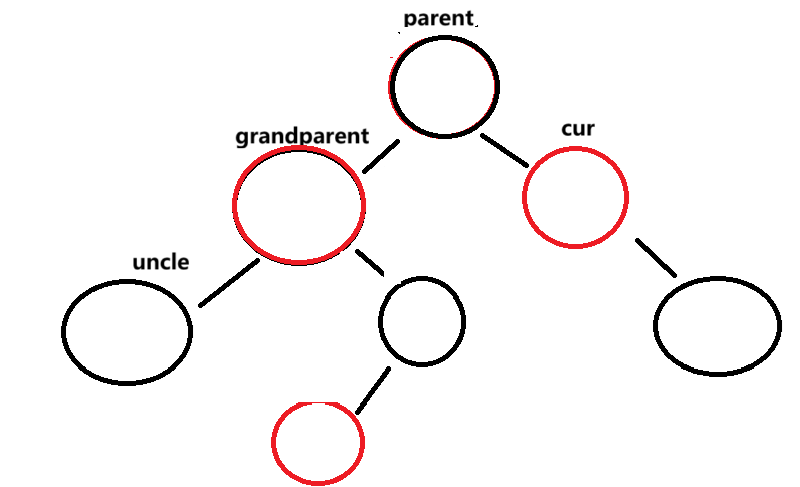
最后更新cur指向parent

parent指向cur.parent

java 复制代码

                    rotateLeft(grandparent);
                    parent.color=BLACK;
                    grandparent.color=RED;
                    cur=parent;
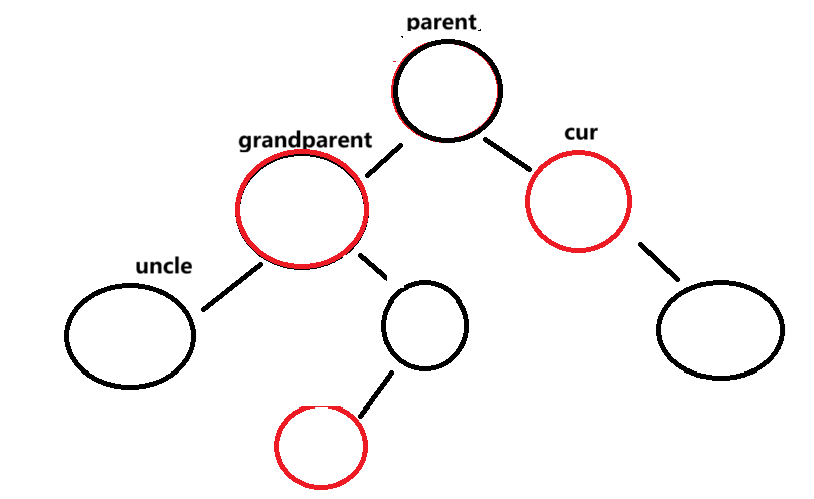
                    parent=cur.parent;

cur == parent.left

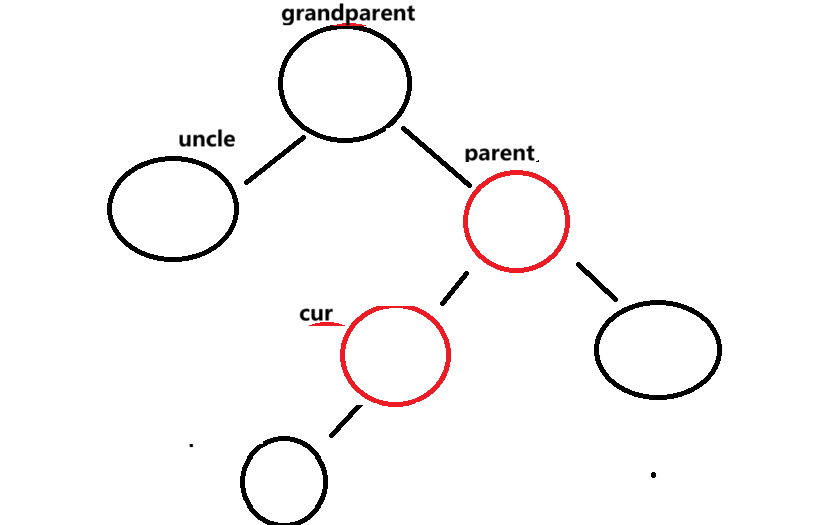
首先右旋parent ，然后更新cur和parent

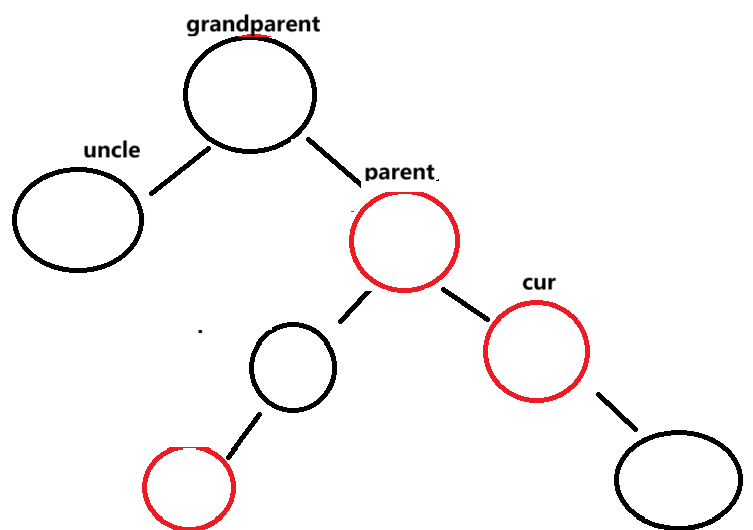
此时情况又变成cur == parent,right

java 复制代码

                    if(cur==parent.left){
                        rotateRight(parent);
                        parent=cur;
                        cur=parent.right;
                    }
                    rotateLeft(grandparent);
                    parent.color=BLACK;
                    grandparent.color=RED;
                    cur=parent;
                    parent=cur.parent;

收尾

此时已经跳出循环，将root置为黑色，最后返回true

红黑树的验证

首先中序遍历，观察是否有序

java 复制代码

    public void inorder(RBTreeNode root) {
        if (root == null) return;
        inorder(root.left);
        System.out.print(root.val + " ");
        inorder(root.right);
    }

然后开始逐一判断每条性质

先判断根节点 ，如果根节点为空那么是红黑树

如果根节点为红节点那么不是红黑树

然后开始判断是否有两个红节点连在一起 ，思路就是递归遍历红黑树，如果这个节点是红节点 ，那么开始判断他的父节点的颜色

java 复制代码

    private boolean CheckRedNode(RBTreeNode node){
        if(node==null) return true;
        if(node.color==RED){
            if(node.parent.color==RED){
                System.out.println("不能存在两个连续的红色节点");
                return false;
            }
        }
        return CheckRedNode(node.left)&&CheckRedNode(node.right);
    }

因为之前判断过根节点不为红色，所以这里不用判断node.parent是否存在，因为根节点进不去if语句

判断每条路径上的黑色节点数是否相同

提前计算其中一条路径的黑色节点数，记录下来(BlackCount)。然后开始递归计算每条路线的黑节点数(PathBlackCount)，当node为空 时，开始判断BlackCount和PathBlackCount是否相等。

java 复制代码

    private boolean CheckBlackCount(RBTreeNode node,int PathBlackCount,int BlackCount){
        if(node==null) return PathBlackCount==BlackCount;
        if(node.color==BLACK) PathBlackCount++;
        return CheckBlackCount(node.left,PathBlackCount,BlackCount)&&
                CheckBlackCount(node.right,PathBlackCount,BlackCount);
    }

AVL树和红黑树的比较

都是高效的平衡二叉树 ，增删查改的时间复杂度都是O(logN) ，红黑树不追求绝对平衡 ，只需保证最长路径不超过最短路径的两倍 ，相对而言降低了插入和旋转的次数，所以在经常进行增删查改的结构中的性能比AVL树高。