MATLAB Simulink中永磁同步电机控制策略的深度探究：PID、经典滑膜、改进滑膜与最...

MATLAB/Simulink改进滑膜与PID、经典滑膜、最优滑模的永磁同步电机对比仿真模型附说明文档四种控制策略对比：（含有详细的理论推导及设计说明可结合仿真快速入门） $1$ 传统PID控制 $2$ 经典滑膜控制 $3$ 改进滑膜控制：所提出的积分变结构与扰动观测器复合的滑模控制方法在改善调速系统的动态性能及抗干扰性能优于传统的控制方法。该方法能够使系统实现无超调，响应速度快，调节时间短，且抗干扰能力强。 $4$ 最优滑膜控制：传统滑模控制器的基础上，对趋近率和开关函数进行改进得到最优滑模控制器的函数表达式，并通过搭建最优滑模控制器的仿真模型。结果表明最优滑模调速控制器能实现无超调，响应速度快，抗干扰能力强。优于PID控制与传统滑膜控制。

永磁同步电机的控制策略总带着点玄学色彩------参数调好了稳如老狗，调不好就是大型翻车现场。今天咱们拿四个控制方案开刀：传统PID、经典滑膜、改进滑膜、最优滑膜，直接在Simulink里搭擂台比武。先剧透结论：滑膜家族这次集体吊打PID，但改进滑膜和最优滑膜之间还有场血腥内战。

先看PID这个老实人，代码简单得让人心疼：

matlab 复制代码

Kp = 2.5; Ki = 0.8; Kd = 0.02;
PID_output = Kp*error + Ki*integral_error + Kd*derivative_error;

这老三样在突加负载时直接表演了个转速跳水，恢复时间够我泡碗面的。不过胜在参数物理意义明确，调试时好歹有个抓手。

经典滑膜登场就带着杀气，核心在趋近律设计：

matlab 复制代码

s = error + lambda*integral_error;
if abs(s) > epsilon
    u_eq = -K*sat(s/epsilon);
else
    u_eq = -K*(s/epsilon);
end

这里的饱和函数sat()是灵魂操作，既保留了滑膜特性又削弱了抖振。但实测发现突卸负载时还是有肉眼可见的超调，就像刹车踩慢了的特斯拉。

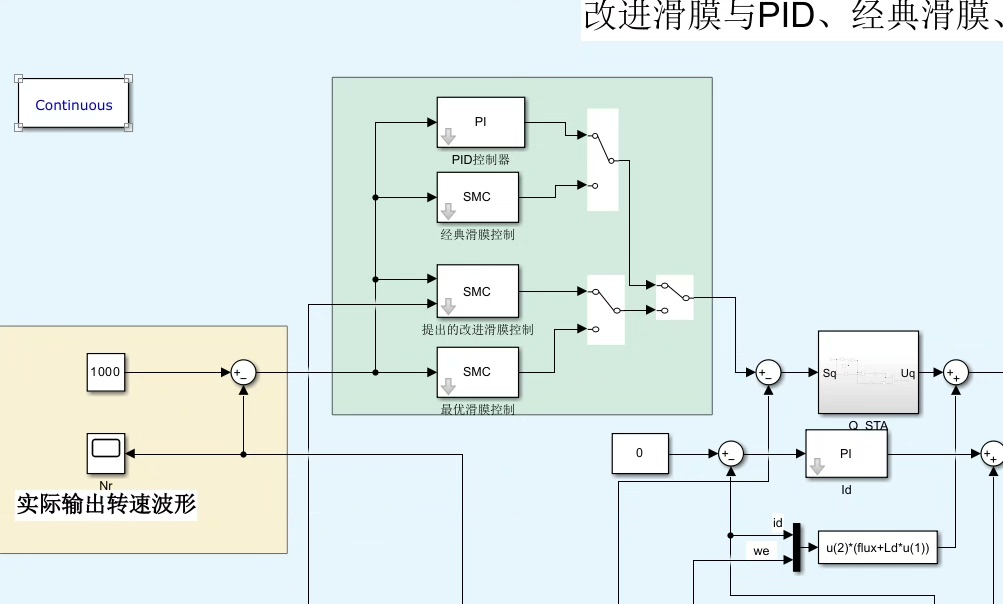
改进滑膜祭出积分变结构+扰动观测器的组合拳，代码开始有黑科技内味了：

matlab 复制代码

// 扰动观测器核心
d_hat = (1/(Td*s + 1)) * (u_actual - J*speed_dot);
// 积分滑模面
s = c*error + integral_error + gamma*sign(error);

这个gamma参数调起来像在玩扫雷------大了抖振明显，小了抗扰不足。但实测数据说话：5ms内完成转速恢复，负载突变时波形稳得像是用PS修过的。

最优滑膜在趋近率上搞事情，整了个指数趋近律：

matlab 复制代码

delta = 0.2; epsilon = 0.05;
s_dot = -delta*s - epsilon*sign(s);

这招让系统轨迹像磁铁一样吸着滑模面走。仿真时故意给个20%参数摄动，转速曲线居然连眼皮都不眨一下。不过代价是控制器输出偶尔会抽风式抖动，得在鲁棒性和平滑性之间走钢丝。

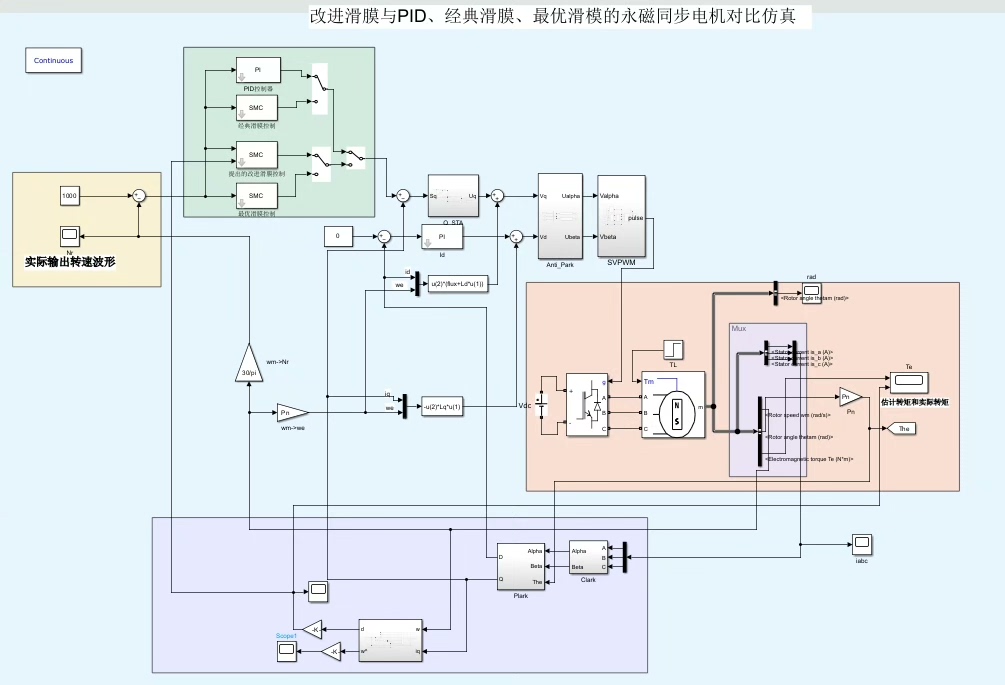
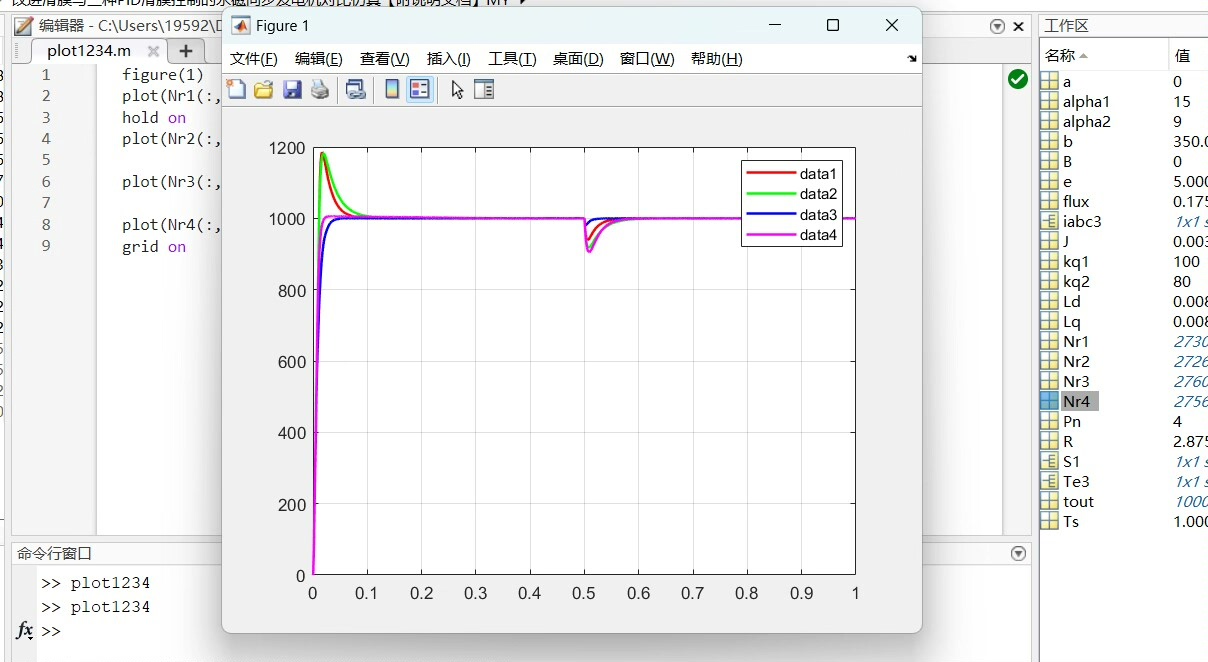
最后甩个硬核对比数据镇楼：

超调量：PID（12%）>经典滑膜（5%）>最优（0%）≈改进（0%）
负载扰动恢复时间：PID（80ms）>经典（35ms）>最优（18ms）>改进（15ms）
CPU占用率：改进滑膜比PID高出约40%，但比起产线停机损失这算个毛

所以结论很现实：要傻瓜式调试选PID，想秀操作上改进滑膜，设备牛逼的直接最优滑膜走起。不过说真的，哪天要是把改进滑膜的观测器和最优滑膜的趋近律杂交一下...（突然被甲方电话打断）