吴恩达机器学习2022 -- Course1 -- Week3（分类问题）

分类问题

[1. 逻辑回归](#1. 逻辑回归)
- [1.1 线性回归不适用于分类问题](#1.1 线性回归不适用于分类问题)
- - 为什么不能直接用线性回归解决分类问题？
- [1.2 逻辑回归模型](#1.2 逻辑回归模型)
- - [1）Sigmoid 函数](#1）Sigmoid 函数)
  - - [Sigmoid 函数的特点](#Sigmoid 函数的特点)
  - 2）逻辑回归模型的构建
- [1.3 决策边界](#1.3 决策边界)
- - 1）什么是决策边界？
  - - 示例1：决策边界为直线
    - 示例2：决策边界为圆
[2. 逻辑回归的代价函数](#2. 逻辑回归的代价函数)
- [2.1 为什么不使用线性回归的平方误差？](#2.1 为什么不使用线性回归的平方误差？)
- [2.2 逻辑回归的损失函数（单个样本）](#2.2 逻辑回归的损失函数（单个样本）)
- [2.3 统一写法（推荐）](#2.3 统一写法（推荐）)
- [2.4 代价函数（整个训练集）](#2.4 代价函数（整个训练集）)
[3. 实现梯度下降](#3. 实现梯度下降)
- [3.1 为什么逻辑回归可以使用梯度下降？](#3.1 为什么逻辑回归可以使用梯度下降？)
- [3.2 梯度下降更新规则](#3.2 梯度下降更新规则)
- - [对权重 w j w_j wj 的梯度：](#对权重 w j w_j wj 的梯度：)
  - [对偏置 b b b 的梯度：](#对偏置 b b b 的梯度：)
- [3.3 梯度下降公式（核心）](#3.3 梯度下降公式（核心）)
[4. 过拟合与正则化](#4. 过拟合与正则化)
- [4.1 什么是过拟合和欠拟合？](#4.1 什么是过拟合和欠拟合？)
- [4.2 为什么过拟合是个问题？](#4.2 为什么过拟合是个问题？)
- [4.3 解决过拟合的三种方法](#4.3 解决过拟合的三种方法)
- [4.4 如何解决过拟合？------ 正则化](#4.4 如何解决过拟合？—— 正则化)
- - [正则化参数 λ \lambda λ 的作用：](#正则化参数 λ \lambda λ 的作用：)
- [4.5 正则化后的梯度更新公式](#4.5 正则化后的梯度更新公式)
小结：逻辑回归相关公式

1. 逻辑回归

1.1 线性回归不适用于分类问题

在监督学习中，我们通常处理两类任务：

回归（Regression）：预测一个连续值，例如房价
分类（Classification）：预测一个离散标签，例如判断邮件是否为垃圾邮件

当输出只有两种可能结果时（如"是/否"、"良性/恶性"），这类问题称为 二元分类（Binary Classification） 。通常用 0 表示负类（如"否"），用 1 表示正类（如"是"）

下图为肿瘤二元分类示意图：

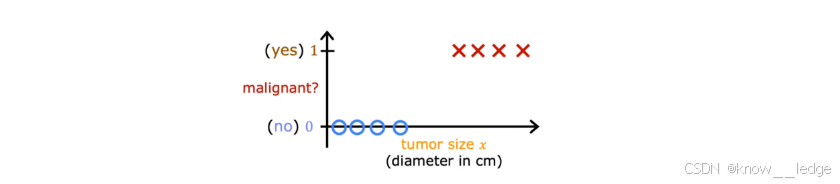
概念明晰：尽管名字叫 " 逻辑回归 " ，但它实际上是一个分类算法，而不是回归算法。这是历史命名造成的误解。

为什么不能直接用线性回归解决分类问题？

我们可以在上方的肿瘤二元分类示意图上用线性回归拟合一条直线：
f w , b ( x ) = w x + b f_{w,b}(x) = wx + b fw,b(x)=wx+b

然后设定一个阈值（例如 0.5）进行分类：

若 f ( x ) < 0.5 f(x) < 0.5 f(x)<0.5，预测为 0（良性）
若 f ( x ) ≥ 0.5 f(x) \geq 0.5 f(x)≥0.5，预测为 1（恶性）

这看起来似乎可行，但存在严重问题

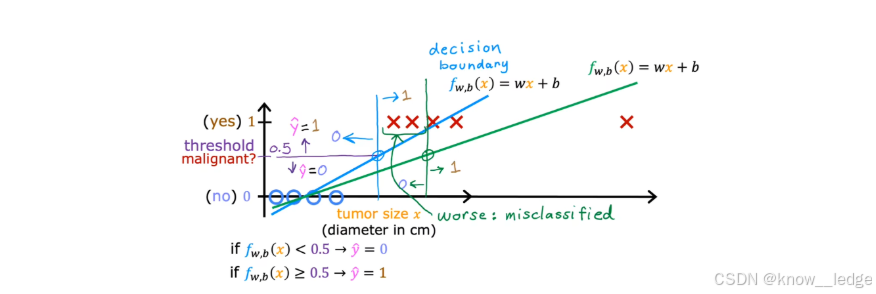
问题一：模型输出可能超出 [0, 1] 范围（输出无界）

线性回归的输出是任意实数。例如：

当 x = 0 x = 0 x=0， f ( x ) = − 1.2 f(x) = -1.2 f(x)=−1.2
当 x = 10 x = 10 x=10， f ( x ) = 3.8 f(x) = 3.8 f(x)=3.8

但分类问题中，我们希望输出表示"属于正类的概率"，而概率必须在 0 到 1 之间

说"恶性概率是" -1.2 "或" 3.8 "没有意义

问题二：对异常值敏感，决策边界不稳定

如果新增一个极端样本（例如一个直径很大的良性肿瘤），线性回归会为了拟合这个点而大幅调整直线斜率，导致原本正确的分类边界被破坏

这是因为线性回归的目标是最小化预测值与真实值之间的平方误差 ，而不是最大化分类准确率

因此，我们需要一种专门用于分类的模型------逻辑回归（Logistic Regression）。

1.2 逻辑回归模型

1）Sigmoid 函数

为了解决线性回归输出无界的问题，逻辑回归引入了一个关键函数：Sigmoid 函数（也称为 Logistic 函数）

它的数学表达式为：

g ( z ) = 1 1 + e − z g(z) = \frac{1}{1 + e^{-z}} g(z)=1+e−z1

Sigmoid 函数的特点

输入 z z z 可以是任意实数（ − ∞ < z < + ∞ -\infty < z < +\infty −∞<z<+∞）；
输出始终在 ( 0 , 1 ) (0, 1) (0,1) 区间内；
当 z = 0 z = 0 z=0 时， g ( z ) = 0.5 g(z) = 0.5 g(z)=0.5；
当 z → + ∞ z \to +\infty z→+∞， g ( z ) → 1 g(z) \to 1 g(z)→1；
当 z → − ∞ z \to -\infty z→−∞， g ( z ) → 0 g(z) \to 0 g(z)→0。

这使得 Sigmoid 函数非常适合用来表示"概率"。

如图为"肿瘤是否恶性"的分类问题（使用 Sigmoid 函数）：

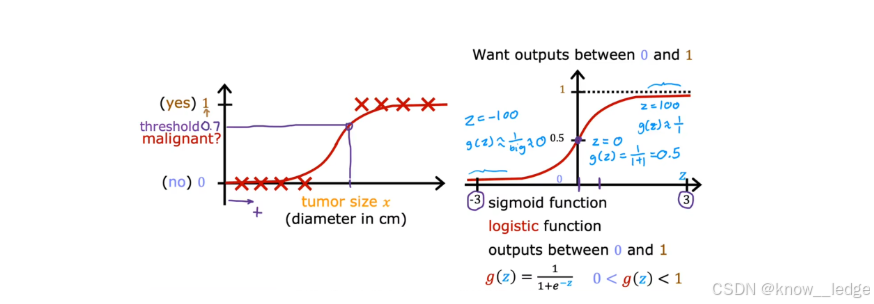
如果模型输出为 0.7 → 表示该肿瘤有 70% 的可能是恶性；

输出为 0.3 → 则表示有 30% 可能是恶性。

2）逻辑回归模型的构建

我们结合线性模型和 Sigmoid 函数，构建完整的逻辑回归模型：

线性部分（z） ：设输入特征向量为 x ⃗ \vec{x} x ，权重向量为 w ⃗ \vec{w} w ，偏置项为 b b b，则：
z = w ⃗ ⋅ x ⃗ + b z = \vec{w} \cdot \vec{x} + b z=w ⋅x +b

这就是我们熟悉的线性组合，可以是单个特征（如肿瘤大小），也可以是多个特征的加权和。

通过 Sigmoid 函数转换为概率 ：将 z z z 代入 Sigmoid 函数转换为概率
f w ⃗ , b ( x ⃗ ) = g ( z ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) f_{\vec{w},b}(\vec{x}) = g(z) = \frac{1}{1 + e^{-(\vec{w} \cdot \vec{x} + b)}} fw ,b(x )=g(z)=1+e−(w ⋅x +b)1

这个输出可以解释为：

在给定特征 x ⃗ \vec{x} x 和参数 w ⃗ , b \vec{w}, b w ,b 的情况下，样本属于正类（ y = 1 y=1 y=1）的概率：

P ( y = 1 ∣ x ⃗ ; w ⃗ , b ) = f w ⃗ , b ( x ⃗ ) P(y=1 \mid \vec{x}; \vec{w}, b) = f_{\vec{w},b}(\vec{x}) P(y=1∣x ;w ,b)=fw ,b(x )

1.3 决策边界

决策边界是逻辑回归模型中非常关键的概念：它决定了"什么时候预测为 1，什么时候预测为 0"。

1）什么是决策边界？

在逻辑回归中，模型输出的是一个概率值：

f w ⃗ , b ( x ⃗ ) = g ( z ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) f_{\vec{w},b}(\vec{x}) = g(z) = \frac{1}{1 + e^{-(\vec{w} \cdot \vec{x} + b)}} fw ,b(x )=g(z)=1+e−(w ⋅x +b)1

其中 w ⃗ ⋅ x ⃗ + b \vec{w} \cdot \vec{x} + b w ⋅x +b 是线性部分， f w ⃗ , b ( x ⃗ ) = g ( z ) f_{\vec{w},b}(\vec{x}) = g(z) fw ,b(x )=g(z) 表示给定输入 x ⃗ \vec{x} x ，样本属于正类（标签为 1）的概率。

虽然模型输出的是一个概率值，但分类任务需要明确的类别（0 或 1）。因此引入决策边界（通常为 0.5）：

若 f w ⃗ , b ( x ⃗ ) ≥ 0.5 f_{\vec{w},b}(\vec{x}) \geq 0.5 fw ,b(x )≥0.5 → 预测为 1（正类）
若 f w ⃗ , b ( x ⃗ ) < 0.5 f_{\vec{w},b}(\vec{x}) < 0.5 fw ,b(x )<0.5 → 预测为 0（负类）

注意：由于 Sigmoid 函数在 z = 0 z = 0 z=0 时输出 0.5，因此上述规则等价于：

若 w ⃗ ⋅ x ⃗ + b ≥ 0 \vec{w} \cdot \vec{x} + b \geq 0 w ⋅x +b≥0 → 预测为 1

若 w ⃗ ⋅ x ⃗ + b < 0 \vec{w} \cdot \vec{x} + b < 0 w ⋅x +b<0 → 预测为 0

这说明：逻辑回归的决策边界仍然是线性的，只是它的输出不再是简单的 0/1，而是带有概率意义的预测

这意味着，决策边界 由等式 w ⃗ ⋅ x ⃗ + b = 0 \vec{w} \cdot \vec{x} + b = 0 w ⋅x +b=0 确定。

示例1：决策边界为直线

对于有两个特征 x 1 x_1 x1 和 x 2 x_2 x2 的情况，逻辑回归的决策边界由以下方程定义：

w 1 x 1 + w 2 x 2 + b = 0 w_1 x_1 + w_2 x_2 + b = 0 w1x1+w2x2+b=0

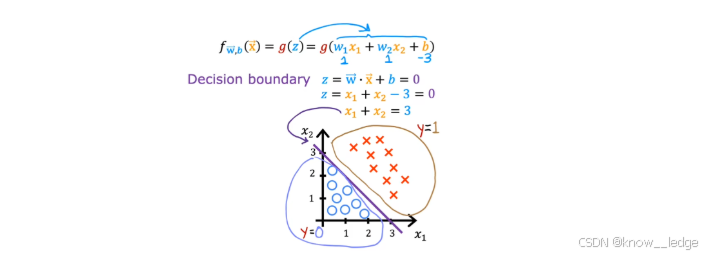
这是一个二维平面上的直线，将样本空间划分为两个区域：

直线右侧的点满足 w 1 x 1 + w 2 x 2 + b > 0 w_1 x_1 + w_2 x_2 + b > 0 w1x1+w2x2+b>0，模型预测为 1

左侧满足 w 1 x 1 + w 2 x 2 + b < 0 w_1 x_1 + w_2 x_2 + b < 0 w1x1+w2x2+b<0，模型预测为 0

例如，若 w 1 = 2 w_1 = 2 w1=2、 w 2 = − 3 w_2 = -3 w2=−3、 b = 1 b = 1 b=1，则决策边界为：

2 x 1 − 3 x 2 + 1 = 0 2x_1 - 3x_2 + 1 = 0 2x1−3x2+1=0

该直线斜率为 2 3 \frac{2}{3} 32。图中通常用不同颜色或标记（如 ○ 和 ×）表示两类样本，而决策边界正好位于它们之间，实现分类分隔。

示例2：决策边界为圆

在某些情况下，数据的自然分界不是直线，而是曲线。例如，当特征之间存在非线性关系时，我们可以构造一个非线性决策边界。

本分类问题中，定义：
z = w 1 x 1 2 + w 2 x 2 2 + b z = w_1 x_1^2 + w_2 x_2^2 + b z=w1x12+w2x22+b

假设参数 w 1 = 1 w_1 = 1 w1=1、 w 2 = 1 w_2 = 1 w2=1、 b = − 1 b = -1 b=−1，则：
z = x 1 2 + x 2 2 − 1 z = x_1^2 + x_2^2 - 1 z=x12+x22−1

决策边界由 g ( z ) = 0.5 g(z) = 0.5 g(z)=0.5 决定，即：
x 1 2 + x 2 2 − 1 = 0 ⇒ x 1 2 + x 2 2 = 1 x_1^2 + x_2^2 - 1 = 0 \quad \Rightarrow \quad x_1^2 + x_2^2 = 1 x12+x22−1=0⇒x12+x22=1

这是一个以原点为中心、半径为 1 的单位圆。

圆内部（ x 1 2 + x 2 2 < 1 x_1^2 + x_2^2 < 1 x12+x22<1）的点被预测为 0（负类）；
圆外部（ x 1 2 + x 2 2 > 1 x_1^2 + x_2^2 > 1 x12+x22>1）的点被预测为 1（正类）；

这说明：虽然模型本身是线性的 ，但通过引入特征变换（如平方项），我们可以在原始空间中实现非线性分类。

2. 逻辑回归的代价函数

提示：log 表示以自然常数 e e e 为底的对数（即 ln）。

2.1 为什么不使用线性回归的平方误差？

在线性回归中，我们使用均方误差（MSE） 作为代价函数：

J ( w , b ) = 1 2 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 J(w, b) = \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2 J(w,b)=2m1i=1∑m(fw,b(x(i))−y(i))2

但逻辑回归不能直接用这个公式！原因如下：

逻辑回归的预测值是通过 Sigmoid 函数 输出的：
f w , b ( x ) = 1 1 + e − ( w x + b ) f_{w,b}(x) = \frac{1}{1 + e^{-(wx + b)}} fw,b(x)=1+e−(wx+b)1

这是一个非线性、S 形的函数，输出始终在 (0,1) 之间。
如果把 Sigmoid 函数代入平方误差公式，得到的代价函数会高度非凸（non-convex），形状像"波浪山"。

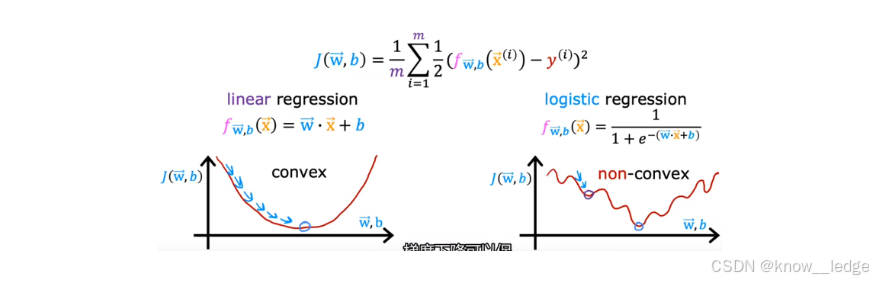
非凸函数有多个局部最小值，梯度下降算法很容易卡在某个"假最低点"，无法找到全局最优解。

所以我们需要一个凸函数（convex） 的代价函数------只有一个"碗底"，保证梯度下降一定能收敛到最优解。

2.2 逻辑回归的损失函数（单个样本）

逻辑回归要使用一种叫 对数损失 的函数

对于单个训练样本 ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i))，其损失函数定义为：

L ( f w , b ( x ( i ) ) , y ( i ) ) = { − log ⁡ ( f w , b ( x ( i ) ) ) , y ( i ) = 1 − log ⁡ ( 1 − f w , b ( x ( i ) ) ) , y ( i ) = 0 L(f_{w,b}(x^{(i)}), y^{(i)}) = \begin{cases} -\log(f_{w,b}(x^{(i)})) ,& \text y^{(i)} = 1 \\ -\log(1 - f_{w,b}(x^{(i)})), & \text y^{(i)} = 0 \end{cases} L(fw,b(x(i)),y(i))={−log(fw,b(x(i))),−log(1−fw,b(x(i))),y(i)=1y(i)=0

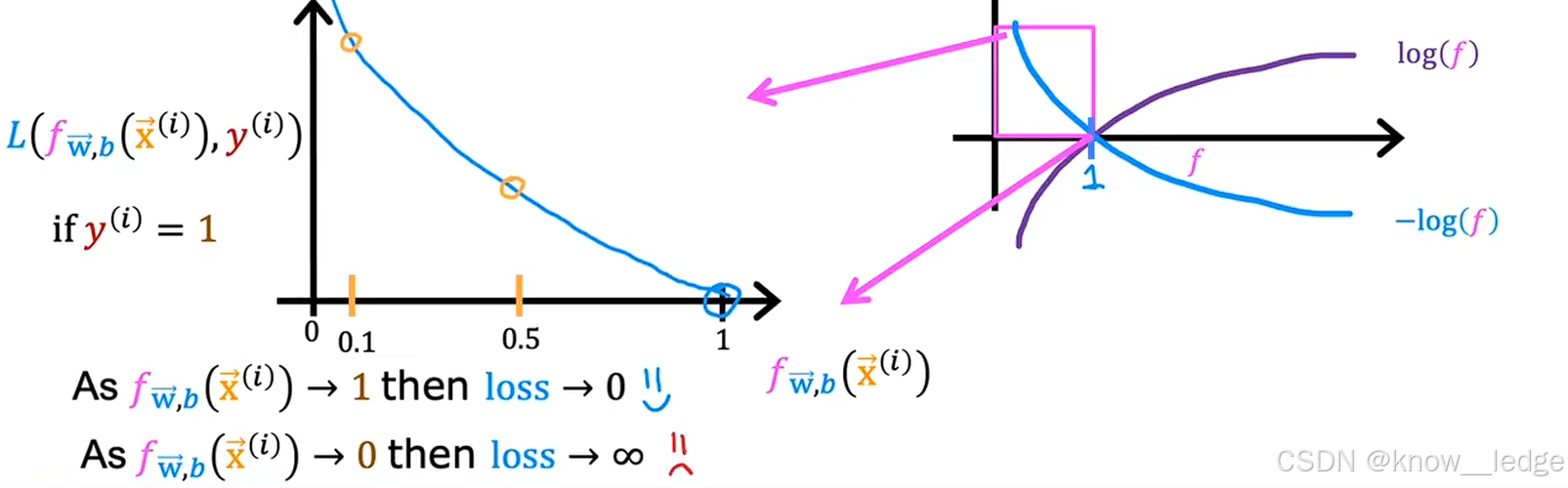
当 y ( i ) = 1 y^{(i)} = 1 y(i)=1 时：

我们希望预测值 f w , b ( x ( i ) ) f_{w,b}(x^{(i)}) fw,b(x(i)) 越接近 1 越好；

若 f → 1 f \to 1 f→1，则 − log ⁡ ( f ) → 0 -\log(f) \to 0 −log(f)→0 → 损失小；

若 f → 0 f \to 0 f→0，则 − log ⁡ ( f ) → + ∞ -\log(f) \to +\infty −log(f)→+∞ → 损失极大。

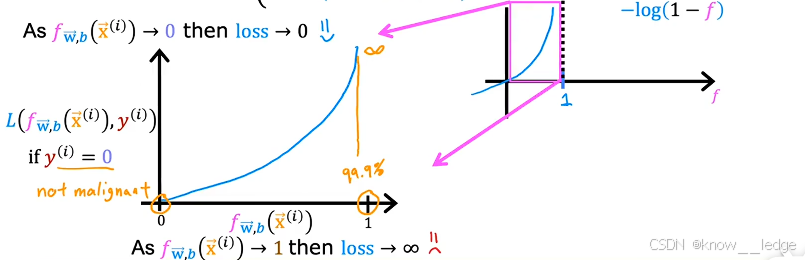
当 y ( i ) = 0 y^{(i)} = 0 y(i)=0 时：

我们希望预测值越接近 0 越好；

若 f → 0 f \to 0 f→0，则 − log ⁡ ( 1 − f ) → 0 -\log(1 - f) \to 0 −log(1−f)→0 → 损失小；

若 f → 1 f \to 1 f→1，则 − log ⁡ ( 1 − f ) → + ∞ -\log(1 - f) \to +\infty −log(1−f)→+∞ → 损失极大。

总结：预测值越接近真实标签，损失越小；越远，损失越大且增长极快。

2.3 统一写法（推荐）

我们可以将分段函数合并为一个简洁表达式：

L ( f w , b ( x ( i ) ) , y ( i ) ) = − y ( i ) log ⁡ ( f w , b ( x ( i ) ) ) − ( 1 − y ( i ) ) log ⁡ ( 1 − f w , b ( x ( i ) ) ) L(f_{w,b}(x^{(i)}), y^{(i)}) = -y^{(i)} \log(f_{w,b}(x^{(i)})) - (1 - y^{(i)}) \log(1 - f_{w,b}(x^{(i)})) L(fw,b(x(i)),y(i))=−y(i)log(fw,b(x(i)))−(1−y(i))log(1−fw,b(x(i)))

验证：

若 y ( i ) = 1 y^{(i)} = 1 y(i)=1：第二项为 0，剩下 − log ⁡ ( f ) -\log(f) −log(f)
若 y ( i ) = 0 y^{(i)} = 0 y(i)=0：第一项为 0，剩下 − log ⁡ ( 1 − f ) -\log(1 - f) −log(1−f)

完美匹配！

2.4 代价函数（整个训练集）

对所有 m m m 个样本取平均，得到总代价函数：

J ( w ⃗ , b ) = 1 m ∑ i = 1 m L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) J(\vec{w}, b) = \frac{1}{m} \sum_{i=1}^{m} L(f_{\vec{w},b}(\vec{x}^{(i)}), y^{(i)}) J(w ,b)=m1i=1∑mL(fw ,b(x (i)),y(i))

代入损失函数表达式：

J ( w ⃗ , b ) = − 1 m ∑ i = 1 m [ y ( i ) log ⁡ ( f w ⃗ , b ( x ⃗ ( i ) ) ) + ( 1 − y ( i ) ) log ⁡ ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] J(\vec{w}, b) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(f_{\vec{w},b}(\vec{x}^{(i)})) + (1 - y^{(i)}) \log(1 - f_{\vec{w},b}(\vec{x}^{(i)})) \right] J(w ,b)=−m1i=1∑m[y(i)log(fw ,b(x (i)))+(1−y(i))log(1−fw ,b(x (i)))]

注意：这里没有 1 2 \frac{1}{2} 21！因为对数损失本身已具备良好的数学性质，无需额外系数简化求导。

物理意义上看，这种代价函数基于统计学中的 最大似然估计 原理，是最自然的选择之一

3. 实现梯度下降

梯度下降 是训练逻辑回归模型的核心方法：通过不断调整参数 w w w 和 b b b，让代价函数最小化。

3.1 为什么逻辑回归可以使用梯度下降？

逻辑回归的代价函数为：

其中：

f w , b ( x ) = 1 1 + e − ( w x + b ) f_{w,b}(x) = \frac{1}{1 + e^{-(wx + b)}} fw,b(x)=1+e−(wx+b)1 是Sigmoid函数；

y ( i ) ∈ { 0 , 1 } y^{(i)} \in \{0, 1\} y(i)∈{0,1} 是真实标签；

m m m 是训练样本数量。

这个代价函数是凸函数，只有一个全局最小值，因此可以使用梯度下降法稳定收敛到最优解

3.2 梯度下降更新规则

我们需要计算代价函数对参数的偏导数：

对权重 w j w_j wj 的梯度：

∂ J ∂ w j = 1 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J}{\partial w_j} = \frac{1}{m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right) x_j^{(i)} ∂wj∂J=m1i=1∑m(fw,b(x(i))−y(i))xj(i)

对偏置 b b b 的梯度：

∂ J ∂ b = 1 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) \frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right) ∂b∂J=m1i=1∑m(fw,b(x(i))−y(i))

3.3 梯度下降公式（核心）

使用学习率 α \alpha α，每次迭代更新参数：

{ w j = w j − α ∂ J ∂ w j = w j − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x ⃗ j ( i ) b = b − α ∂ J ∂ b = b − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) j = 1 , 2 , ... , n . \begin{cases} w_j = w_j - \alpha \dfrac{\partial J}{\partial w_j} = w_j - \dfrac{\alpha}{m} \displaystyle\sum_{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right) \cdot \vec{x}j^{(i)} \\ \\ b = b - \alpha \dfrac{\partial J}{\partial b} = b - \dfrac{\alpha}{m} \displaystyle\sum{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right) \end{cases} \quad \text j = 1,2,\dots,n. ⎩ ⎨ ⎧wj=wj−α∂wj∂J=wj−mαi=1∑m(fw ,b(x (i))−y(i))⋅x j(i)b=b−α∂b∂J=b−mαi=1∑m(fw ,b(x (i))−y(i))j=1,2,...,n.

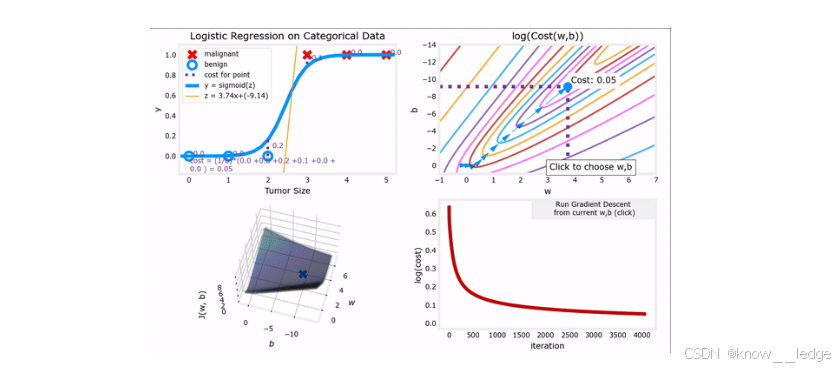
左图：Sigmoid 曲线拟合肿瘤数据，显示分类边界；

右图：在参数空间中，梯度下降沿着代价函数的"下坡"方向移动，逐步逼近最优解 ( w ∗ , b ∗ ) (w^*, b^*) (w∗,b∗)。

虽然模型不同，但梯度下降的数学形式与线性回归相同------这是计算上的巧合，也是其高效性的体现。

4. 过拟合与正则化

当模型在训练数据上表现很好，但在新数据上表现差时，说明它"学得太死"了------这就是过拟合 。

本节将带你理解什么是过拟合和欠拟合，并学习如何用 正则化 来解决这个问题。

4.1 什么是过拟合和欠拟合？

我们通过一个简单的例子来理解三种模型状态：

假设我们要根据房屋面积预测房价，有以下三种情况：

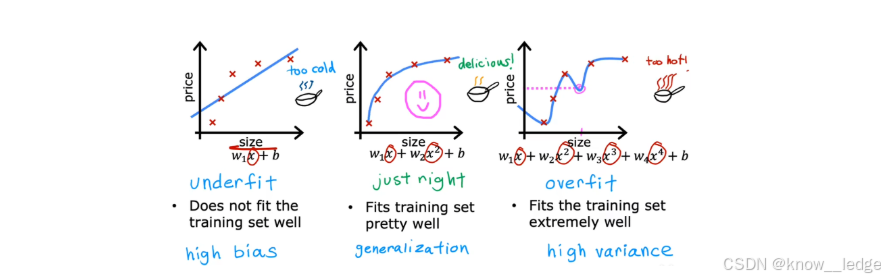
左图为欠拟合

模型太简单（比如只用一条水平线拟合）；
无法捕捉数据的基本规律；
训练误差大，测试误差也大。

原因：模型复杂度太低，或特征太少。

中图为理想拟合

模型能抓住数据的整体趋势；
在训练集和新数据上都表现良好。

右图为过拟合

模型太复杂（比如用高阶多项式穿过每一个点）；
完美拟合训练数据，却把噪声也当成了规律；
训练误差很小，但测试误差很大。

原因：模型复杂度太高，或训练数据太少。

4.2 为什么过拟合是个问题？

过拟合的模型就像一个"死记硬背的学生"：

考试前把练习题答案全背下来 → 训练准确率 100%；
但遇到新题就懵了 → 实际应用效果差。

在机器学习中，我们的目标是泛化能力（Generalization） ：

能对从未见过的数据做出准确预测。

过拟合会严重损害泛化能力！

4.3 解决过拟合的三种方法

扩大训练集：此时即使有很多特征，相比于训练集很小时，其拟合曲线也会相对平滑。
缺点是不一定能获取更多的训练数据。

减少特征数：也称为"特征选择"。"特征选择"除了靠直觉，在Course2中也会介绍一种自动选择特征的方法。缺点是有可能会丢弃有用特征。

正则化：保留所有的特征，但对于某个很大的特征 x j x_j xj，减小其参数 w j w_j wj（通常不会调整参数 b b b）

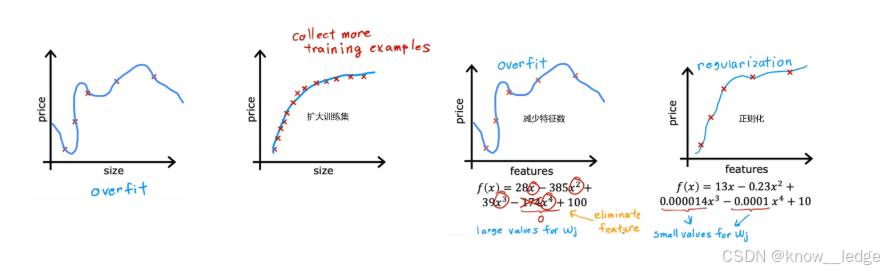
4.4 如何解决过拟合？------ 正则化

正则化是一种防止过拟合的技术，核心思想是：

在代价函数中加入一个"惩罚项"，限制模型参数不要变得太大。

为什么有效？

大的参数值往往意味着模型在"强行拟合噪声"；

限制参数大小，相当于让模型变得更"平滑"、"简单"。

正则化后的代价函数：

我们在原始代价函数后面加上一个正则项：

J ( w ⃗ , b ) = 1 m ∑ i = 1 m L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) + λ 2 m ∑ j = 1 n w j 2 , λ > 0 J(\vec{w}, b) = \frac{1}{m} \sum_{i=1}^{m} L(f_{\vec{w},b}(\vec{x}^{(i)}), y^{(i)}) + \frac{\lambda}{2m} \sum_{j=1}^{n} w_j^2, \quad \lambda > 0 J(w ,b)=m1i=1∑mL(fw ,b(x (i)),y(i))+2mλj=1∑nwj2,λ>0

注：正则化通常不包含偏置项 b b b ，因此 λ 2 m b 2 \frac{\lambda}{2m} b^2 2mλb2 一般省略。

其中：

J ( w , b ) J(w, b) J(w,b) 是原始的逻辑回归代价函数；
λ \lambda λ（lambda）是正则化参数，控制惩罚力度；
m m m 是样本数量；
n n n 是特征数量；
通常不对偏置项 b b b 进行正则化。

正则化参数 λ \lambda λ 的作用：

λ \lambda λ 值	效果
太小（如 0）	几乎无正则化 → 可能过拟合
合适	平衡拟合与泛化 → 最佳性能
太大（如 10000）	参数被过度压缩 → 可能欠拟合

通常通过交叉验证（Cross-Validation）来选择最佳 λ \lambda λ

4.5 正则化后的梯度更新公式

由于代价函数变了，梯度也要相应调整

对于每个权重 w j w_j wj（ j = 1 , 2 , . . . , n j = 1, 2, ..., n j=1,2,...,n）：

∂ J ∂ w j = ∂ J ∂ w j + λ m w j \frac{\partial J_{\text{}}}{\partial w_j} = \frac{\partial J}{\partial w_j} + \frac{\lambda}{m} w_j ∂wj∂J=∂wj∂J+mλwj

因此，梯度下降的更新规则变为：

w j = w j − α ∂ J ∂ w j = w j − α m ( ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] + λ w j ) w_j = w_j - \alpha \dfrac{\partial J}{\partial w_j} = w_j - \dfrac{\alpha}{m} \left( \displaystyle\sum_{i=1}^{m} \left[ (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right] + \lambda w_j \right) wj=wj−α∂wj∂J=wj−mα(i=1∑m[(fw ,b(x (i))−y(i))⋅xj(i)]+λwj)
j = 1 , 2 , ... , n j = 1,2,\dots,n j=1,2,...,n

而偏置项 b b b 不变：

b = b − α ∂ J ∂ b = b − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) b = b - \alpha \dfrac{\partial J}{\partial b} = b - \dfrac{\alpha}{m} \displaystyle\sum_{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right) b=b−α∂b∂J=b−mαi=1∑m(fw ,b(x (i))−y(i))

注意：这个额外的 λ m w j \frac{\lambda}{m} w_j mλwj 项会让 w j w_j wj 在每次更新时"自动缩小一点"，从而防止它变得过大。

下面来进一步分析参数的更新过程(同样也适用于"逻辑回归"中的正则方法)：

w j = w j − α m ( ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] + λ w j ) = ( 1 − α λ m ) w j ⏟ 每次更新自动缩小 w j − α m ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] ⏟ 常规更新 \begin{aligned} w_j &= w_j - \frac{\alpha}{m} \left( \sum_{i=1}^{m} \left[ (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right] + \lambda w_j \right) \\ &= \underbrace{(1 - \alpha \frac{\lambda}{m}) w_j}{\text{每次更新自动缩小} w_j} - \underbrace{\frac{\alpha}{m} \sum{i=1}^{m} \left[ (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right]}_{\text{常规更新}} \end{aligned} wj=wj−mα(i=1∑m[(fw ,b(x (i))−y(i))⋅xj(i)]+λwj)=每次更新自动缩小wj (1−αmλ)wj−常规更新 mαi=1∑m[(fw ,b(x (i))−y(i))⋅xj(i)]

第一项：添加正则化后，会在每次迭代过程中，都使参数 w j w_j wj 乘以一个略小于 1 的常数。

第二项：对于非正则化的线性回归，正常的梯度下降法更新过程。

小结：逻辑回归相关公式

逻辑回归模型：
f w ⃗ , b ( x ⃗ ) = g ( z ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) f_{\vec{w},b}(\vec{x}) = g(z) = \frac{1}{1 + e^{-(\vec{w} \cdot \vec{x} + b)}} fw ,b(x )=g(z)=1+e−(w ⋅x +b)1
代价函数：
J ( w ⃗ , b ) = − 1 m ∑ i = 1 m [ y ( i ) log ⁡ ( f w ⃗ , b ( x ⃗ ( i ) ) ) + ( 1 − y ( i ) ) log ⁡ ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] + λ 2 m ∑ j = 1 n w j 2 , λ > 0 J(\vec{w}, b) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(f_{\vec{w},b}(\vec{x}^{(i)})) + (1 - y^{(i)}) \log(1 - f_{\vec{w},b}(\vec{x}^{(i)}))\right]+ \frac{\lambda}{2m} \sum_{j=1}^{n} w_j^2 , \quad \lambda > 0 J(w ,b)=−m1i=1∑m[y(i)log(fw ,b(x (i)))+(1−y(i))log(1−fw ,b(x (i)))]+2mλj=1∑nwj2,λ>0
梯度下降：
{ w j = w j − α ∂ J ∂ w j = w j − α m ( ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] + λ w j ) b = b − α ∂ J ∂ b = b − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) j = 1 , 2 , ... , n . \begin{cases} w_j = w_j - \alpha \dfrac{\partial J}{\partial w_j} = w_j - \dfrac{\alpha}{m} \left( \displaystyle\sum_{i=1}^{m} \left[ (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right] + \lambda w_j \right) \\ \\ b = b - \alpha \dfrac{\partial J}{\partial b} = b - \dfrac{\alpha}{m} \displaystyle\sum_{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right) \end{cases} \quad \text j = 1,2,\dots,n. ⎩ ⎨ ⎧wj=wj−α∂wj∂J=wj−mα(i=1∑m[(fw ,b(x (i))−y(i))⋅xj(i)]+λwj)b=b−α∂b∂J=b−mαi=1∑m(fw ,b(x (i))−y(i))j=1,2,...,n.