考研数学：多元函数微分学

多元函数微分学

可微的定义

设函数

f=f(x,y) f=f(x,y) f=f(x,y)

在点 (x0,y0)(x_0,y_0)(x0,y0) 的邻域内有定义。

我们说 fff 在 (x0,y0)(x_0,y_0)(x0,y0) 可微 ，如果存在常数 A,BA,BA,B，使得当 (h,k)→(0,0)(h,k)\to(0,0)(h,k)→(0,0) 时：

f(x0+h,y0+k)−f(x0,y0)=Ah+Bk+o(h2+k2). f(x_0+h,y_0+k)-f(x_0,y_0) =Ah+Bk + o\big(\sqrt{h^2+k^2}\big). f(x0+h,y0+k)−f(x0,y0)=Ah+Bk+o(h2+k2 ).

其中

o(ρ) 是 ρ=h2+k2 的高阶无穷小 o(\rho) \text{ 是 }\rho=\sqrt{h^2+k^2}\text{ 的高阶无穷小} o(ρ) 是 ρ=h2+k2 的高阶无穷小

如果偏导数 fx,fyf_x,f_yfx,fy 在点存在，则可微条件可写成：

f(x0+h,y0+k)−f(x0,y0)=fx(x0,y0)h+fy(x0,y0)k+o(h2+k2) \boxed{ f(x_0+h,y_0+k)-f(x_0,y_0) = f_x(x_0,y_0)h + f_y(x_0,y_0)k + o(\sqrt{h^2+k^2}) } f(x0+h,y0+k)−f(x0,y0)=fx(x0,y0)h+fy(x0,y0)k+o(h2+k2 )

即：

函数的增量 ≈ 线性部分 + 一个远小于距离的误差项。

线性部分就是函数的 线性近似（全微分）：

df=fx dx+fy dy. df = f_x\,dx + f_y\,dy. df=fxdx+fydy.

⭐ 一句话总结

多元函数在某点可微，表示：
函数在该点的增量能被一个线性函数（全微分）精确逼近，其误差比距离小得多。

下面是多元函数微分学中几种常见说法的关系

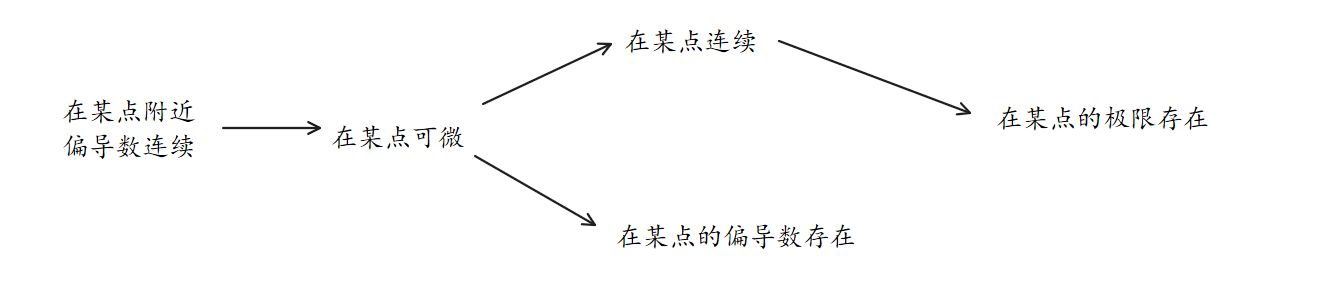
如果一个二元函数在某点的两个偏导数都存在，请问能否推出他在该点连续？

不能！下面给你一个经典反例。

定义函数

f(x,y)={xyx2+y2,(x,y)≠(0,0),0,(x,y)=(0,0). f(x,y)= \begin{cases} \frac{xy}{x^2+y^2}, & (x,y)\neq (0,0),\\[4pt] 0, & (x,y)=(0,0). \end{cases} f(x,y)={x2+y2xy,0,(x,y)=(0,0),(x,y)=(0,0).

我们检查它在 (0,0)(0,0)(0,0) 的偏导：

1️⃣ 计算 fx(0,0)f_x(0,0)fx(0,0)

fx(0,0)=lim⁡h→0f(h,0)−f(0,0)h=lim⁡h→00h=0. f_x(0,0)=\lim_{h\to0}\frac{f(h,0)-f(0,0)}{h} =\lim_{h\to0}\frac{0}{h}=0. fx(0,0)=h→0limhf(h,0)−f(0,0)=h→0limh0=0.

2️⃣ 计算 fy(0,0)f_y(0,0)fy(0,0)

fy(0,0)=lim⁡k→0f(0,k)−f(0,0)k=lim⁡k→00k=0. f_y(0,0)=\lim_{k\to0}\frac{f(0,k)-f(0,0)}{k} =\lim_{k\to0}\frac{0}{k}=0. fy(0,0)=k→0limkf(0,k)−f(0,0)=k→0limk0=0.

所以两个偏导数都存在，且都是 0。

但：fff 在 (0,0)(0,0)(0,0) 不连续

沿直线 y=xy=xy=x 取极限：

f(x,x)=x⋅xx2+x2=12. f(x,x)=\frac{x\cdot x}{x^2+x^2}=\frac12. f(x,x)=x2+x2x⋅x=21.

显然

lim⁡(x,y)→(0,0)f(x,y) \lim_{(x,y)\to(0,0)} f(x,y) (x,y)→(0,0)limf(x,y)

不存在（至少不等于 f(0,0)=0f(0,0)=0f(0,0)=0）。

所以 fff 在该点不连续。

⭐ 结论（必须记住）

二元函数在某点有偏导数是很弱的条件，不能推出连续，更不能推出可微。

梯度、散度、旋度

梯度

定义：设函数z=f(x,y)z = f(x, y)z=f(x,y)在平面区域DDD内具有一阶连续偏导数，则它在点P(x,y)P(x, y)P(x,y)的梯度定义为向量gradf(x,y)=∂f∂xi⃗+∂f∂yj⃗\text{grad}f(x, y) = \frac{\partial f}{\partial x}\vec{i} + \frac{\partial f}{\partial y}\vec{j}gradf(x,y)=∂x∂fi +∂y∂fj （对于三元函数u=f(x,y,z)u = f(x, y, z)u=f(x,y,z)，梯度为gradu=∂u∂xi⃗+∂u∂yj⃗+∂u∂zk⃗\text{grad}u = \frac{\partial u}{\partial x}\vec{i} + \frac{\partial u}{\partial y}\vec{j} + \frac{\partial u}{\partial z}\vec{k}gradu=∂x∂ui +∂y∂uj +∂z∂uk ）。
几何意义 ：梯度的方向是函数在该点增长最快 的方向，其模长是函数在该方向上的最大变化率。例如，在等高线图中（如图18-7(b)），梯度方向垂直于等高线f(x,y)=hf(x, y) = hf(x,y)=h，且指向函数值增大的一侧。
物理意义：可表示物理量（如温度、电势）的变化率方向，比如温度场中梯度方向是温度升高最快的方向。

散度

定义：设向量场A⃗(x,y,z)=P(x,y,z)i⃗+Q(x,y,z)j⃗+R(x,y,z)k⃗\vec{A}(x, y, z) = P(x, y, z)\vec{i} + Q(x, y, z)\vec{j} + R(x, y, z)\vec{k}A (x,y,z)=P(x,y,z)i +Q(x,y,z)j +R(x,y,z)k ，其中P,Q,RP, Q, RP,Q,R具有一阶连续偏导数，则A⃗\vec{A}A 的散度定义为divA⃗=∂P∂x+∂Q∂y+∂R∂z\text{div}\vec{A} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}divA =∂x∂P+∂y∂Q+∂z∂R（也可表示为∇⋅A⃗\nabla \cdot \vec{A}∇⋅A ，其中∇=∂∂xi⃗+∂∂yj⃗+∂∂zk⃗\nabla = \frac{\partial}{\partial x}\vec{i} + \frac{\partial}{\partial y}\vec{j} + \frac{\partial}{\partial z}\vec{k}∇=∂x∂i +∂y∂j +∂z∂k 是哈密顿算子）。
物理意义 ：描述向量场在某点的"发散 "或"汇聚 "程度。若divA⃗>0\text{div}\vec{A} > 0divA >0，该点是"源"（如点电荷的电场在电荷处散度为正）；若divA⃗<0\text{div}\vec{A} < 0divA <0，该点是"汇"；若divA⃗=0\text{div}\vec{A} = 0divA =0，则向量场是无源场（如磁场）。

旋度

定义：设向量场A⃗(x,y,z)=P(x,y,z)i⃗+Q(x,y,z)j⃗+R(x,y,z)k⃗\vec{A}(x, y, z) = P(x, y, z)\vec{i} + Q(x, y, z)\vec{j} + R(x, y, z)\vec{k}A (x,y,z)=P(x,y,z)i +Q(x,y,z)j +R(x,y,z)k ，其中P,Q,RP, Q, RP,Q,R具有一阶连续偏导数，则A⃗\vec{A}A 的旋度定义为
rotA⃗=(∂R∂y−∂Q∂z)i⃗+(∂P∂z−∂R∂x)j⃗+(∂Q∂x−∂P∂y)k⃗\text{rot}\vec{A} = \left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right)\vec{i} + \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right)\vec{j} + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right)\vec{k}rotA =(∂y∂R−∂z∂Q)i +(∂z∂P−∂x∂R)j +(∂x∂Q−∂y∂P)k
也可表示为∇×A⃗\nabla \times \vec{A}∇×A （哈密顿算子叉乘向量场）。
物理意义 ：描述向量场在某点的"旋转 "强度和方向。旋度的方向由右手螺旋定则确定，模长表示单位面积上向量场的环量最大值。若rotA⃗=0⃗\text{rot}\vec{A} = \vec{0}rotA =0 ，则向量场是无旋场（如保守力场，重力场、静电场都是无旋场）；反之则是有旋场（如磁场、涡旋电场）。

方向导数

定义：设函数z=f(x,y)z = f(x, y)z=f(x,y)在点P(x,y)P(x, y)P(x,y)的某一邻域内有定义，自点PPP引射线lll，在lll上取一点P′(x+Δx,y+Δy)P'(x + \Delta x, y + \Delta y)P′(x+Δx,y+Δy)，记ρ=(Δx)2+(Δy)2\rho = \sqrt{(\Delta x)^2 + (\Delta y)^2}ρ=(Δx)2+(Δy)2 。若极限lim⁡ρ→0f(x+Δx,y+Δy)−f(x,y)ρ\lim_{\rho \to 0} \frac{f(x + \Delta x, y + \Delta y) - f(x, y)}{\rho}limρ→0ρf(x+Δx,y+Δy)−f(x,y)存在，则称此极限为函数f(x,y)f(x, y)f(x,y)在点PPP沿方向lll的方向导数 ，记作∂f∂l\frac{\partial f}{\partial l}∂l∂f。对于三元函数u=f(x,y,z)u = f(x, y, z)u=f(x,y,z)，方向导数定义类似。
计算公式 ：若函数f(x,y)f(x, y)f(x,y)在点P(x,y)P(x, y)P(x,y)可微，方向lll的方向余弦为cos⁡α,cos⁡β\cos\alpha, \cos\betacosα,cosβ，则方向导数为
∂f∂l=∂f∂xcos⁡α+∂f∂ycos⁡β\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x}\cos\alpha + \frac{\partial f}{\partial y}\cos\beta∂l∂f=∂x∂fcosα+∂y∂fcosβ

对于三元函数，公式扩展为∂f∂l=∂f∂xcos⁡α+∂f∂ycos⁡β+∂f∂zcos⁡γ\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x}\cos\alpha + \frac{\partial f}{\partial y}\cos\beta + \frac{\partial f}{\partial z}\cos\gamma∂l∂f=∂x∂fcosα+∂y∂fcosβ+∂z∂fcosγ（其中cos⁡α,cos⁡β,cos⁡γ\cos\alpha, \cos\beta, \cos\gammacosα,cosβ,cosγ是方向lll的方向余弦）。
与梯度的关系 ：方向导数可表示为梯度与方向单位向量的点积，即∂f∂l=gradf⋅e⃗l\frac{\partial f}{\partial l} = \text{grad}f \cdot \vec{e}_l∂l∂f=gradf⋅e l（其中e⃗l\vec{e}_le l是方向lll的单位向量）。这说明梯度方向是方向导数最大的方向，且最大方向导数的值等于梯度的模长。
几何与物理意义：几何上表示函数在某点沿指定方向的变化率；物理上可用于描述物理量（如温度、浓度）沿特定方向的变化速率，例如温度场中某点沿风向的温度变化率可通过方向导数计算。

拉格朗日乘数法

什么是拉格朗日乘数法？拉格朗日乘数法用来干啥的？

拉格朗日乘数法解决的问题就是：多元函数在约束条件下的极值问题

在实际问题中，我们常常需要在"满足某些限制条件"的前提下，寻找目标函数的最大值或最小值。例如：

经济学中：在"成本固定"的约束下，最大化产量；或在"产量固定"的约束下，最小化成本。
物理学中：在"能量守恒"的约束下，寻找系统的稳定状态（势能极值）。
几何中：寻找"到原点距离最近的椭圆上的点"（目标函数：距离；约束条件：椭圆方程）。

约束条件下的极值问题的数学本质可分为两类

问题类型	数学形式	核心特点
单个等式约束	目标函数：f(x,y)f(x,y)f(x,y)（或多元函数）约束条件：g(x,y)=0g(x,y)=0g(x,y)=0	仅一个限制条件，且为等式
多个等式约束	目标函数：f(x,y,z)f(x,y,z)f(x,y,z)（或多元函数）约束条件：g1(x,y,z)=0g_1(x,y,z)=0g1(x,y,z)=0，g2(x,y,z)=0g_2(x,y,z)=0g2(x,y,z)=0	多个限制条件，均为等式

如何用拉格朗日乘数法解决条件极值问题呢？

下面我们先以"二元函数+单个约束"为例，来具体说明如何使用拉格朗日乘数法（多元函数+多个等式约束的做法是类似的，你会二元函数+单个约束，就肯定会后面的）

步骤1：明确目标函数与约束条件

首先将实际问题转化为数学形式，确定：

目标函数 f(x,y)f(x,y)f(x,y)（需最大化或最小化的量）；
约束条件 g(x,y)=0g(x,y)=0g(x,y)=0（将约束等式整理为"右边=0"的形式）。

示例：寻找椭圆 x2+2y2=1x^2 + 2y^2 = 1x2+2y2=1 上到原点距离最近的点（距离公式：d=x2+y2d=\sqrt{x^2+y^2}d=x2+y2 ，为简化计算，可令目标函数为 f(x,y)=x2+y2f(x,y)=x^2+y^2f(x,y)=x2+y2，因 ⋅\sqrt{\cdot}⋅ 是单调函数，f(x,y)f(x,y)f(x,y) 与 ddd 的极值点一致）。

目标函数：f(x,y)=x2+y2f(x,y) = x^2 + y^2f(x,y)=x2+y2（最小化）；
约束条件：g(x,y)=x2+2y2−1=0g(x,y) = x^2 + 2y^2 - 1 = 0g(x,y)=x2+2y2−1=0。

步骤2：构造拉格朗日函数

根据定义，引入乘数 λ\lambdaλ，构建 L(x,y,λ)L(x,y,\lambda)L(x,y,λ)：
L(x,y,λ)=f(x,y)−λ⋅g(x,y)L(x,y,\lambda) = f(x,y) - \lambda \cdot g(x,y)L(x,y,λ)=f(x,y)−λ⋅g(x,y)

示例：
L(x,y,λ)=(x2+y2)−λ⋅(x2+2y2−1)L(x,y,\lambda) = (x^2 + y^2) - \lambda \cdot (x^2 + 2y^2 - 1)L(x,y,λ)=(x2+y2)−λ⋅(x2+2y2−1)

步骤3：求偏导并建立方程组

对 LLL 分别求关于 x,y,λx,y,\lambdax,y,λ 的偏导数，令偏导数等于0，得到方程组：
{∂L∂x=0∂L∂y=0∂L∂λ=0\begin{cases} \frac{\partial L}{\partial x} = 0 \\ \frac{\partial L}{\partial y} = 0 \\ \frac{\partial L}{\partial \lambda} = 0 \end{cases}⎩ ⎨ ⎧∂x∂L=0∂y∂L=0∂λ∂L=0

示例：

∂L∂x=2x−2λx=0\frac{\partial L}{\partial x} = 2x - 2\lambda x = 0∂x∂L=2x−2λx=0 → 2x(1−λ)=02x(1 - \lambda) = 02x(1−λ)=0 （1）
∂L∂y=2y−4λy=0\frac{\partial L}{\partial y} = 2y - 4\lambda y = 0∂y∂L=2y−4λy=0 → 2y(1−2λ)=02y(1 - 2\lambda) = 02y(1−2λ)=0 （2）
∂L∂λ=−(x2+2y2−1)=0\frac{\partial L}{\partial \lambda} = -(x^2 + 2y^2 - 1) = 0∂λ∂L=−(x2+2y2−1)=0 → x2+2y2=1x^2 + 2y^2 = 1x2+2y2=1 （3）

步骤4：解方程组并验证极值

解上述方程组，得到可能的极值点 (x,y)(x,y)(x,y)，再通过实际意义或二阶导数判断其是否为最大值/最小值。

示例求解：

由方程（1）：x=0x=0x=0 或 λ=1\lambda=1λ=1；
- 若 x=0x=0x=0，代入方程（3）：0+2y2=10 + 2y^2 = 10+2y2=1 → y=±22y=\pm \frac{\sqrt{2}}{2}y=±22 ，此时代入方程（2）：2⋅(±22)⋅(1−2λ)=02 \cdot (\pm \frac{\sqrt{2}}{2}) \cdot (1 - 2\lambda) = 02⋅(±22 )⋅(1−2λ)=0 → λ=12\lambda=\frac{1}{2}λ=21（有效），得到点 (0,22)(0, \frac{\sqrt{2}}{2})(0,22 ) 和 (0,−22)(0, -\frac{\sqrt{2}}{2})(0,−22 )，对应的 f(x,y)=0+(22)2=12f(x,y)=0 + (\frac{\sqrt{2}}{2})^2 = \frac{1}{2}f(x,y)=0+(22 )2=21；
- 若 λ=1\lambda=1λ=1，代入方程（2）：2y(1−2⋅1)=−2y=02y(1 - 2 \cdot 1) = -2y = 02y(1−2⋅1)=−2y=0 → y=0y=0y=0，再代入方程（3）：x2=1x^2 = 1x2=1 → x=±1x=\pm 1x=±1，得到点 (1,0)(1,0)(1,0) 和 (−1,0)(-1,0)(−1,0)，对应的 f(x,y)=1+0=1f(x,y)=1 + 0 = 1f(x,y)=1+0=1。
验证极值：因 f(x,y)f(x,y)f(x,y) 表示距离的平方，12<1\frac{1}{2} < 121<1，故 (0,±22)(0, \pm \frac{\sqrt{2}}{2})(0,±22 ) 是"到原点最近的点"，最近距离为 12=22\sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2}21 =22 。

为什么我用拉格朗日乘数法能找到极值？

要理解原理，我们先从二元函数+单个约束的简单场景切入，再推广到多元情况。

1. 极值问题的几何本质：梯度平行

假设我们要解决：

目标函数：z=f(x,y)z=f(x,y)z=f(x,y)（可理解为三维空间中的曲面，其等高线为平面上的曲线族 f(x,y)=cf(x,y)=cf(x,y)=c，ccc 为常数）；
约束条件：g(x,y)=0g(x,y)=0g(x,y)=0（可理解为平面上的一条曲线，即"约束曲线"）。

我们的目标是找到约束曲线 g(x,y)=0g(x,y)=0g(x,y)=0 与某条等高线 f(x,y)=cf(x,y)=cf(x,y)=c 的切点 ------因为只有在切点处，目标函数 f(x,y)f(x,y)f(x,y) 才能取得极值：

若两者相交（非相切），则沿约束曲线移动时，f(x,y)f(x,y)f(x,y) 的值会继续增大或减小，未达极值；
若两者相切，则在该点处，等高线 f(x,y)=cf(x,y)=cf(x,y)=c 与约束曲线 g(x,y)=0g(x,y)=0g(x,y)=0 的切线方向一致 ，即它们的法向量平行。

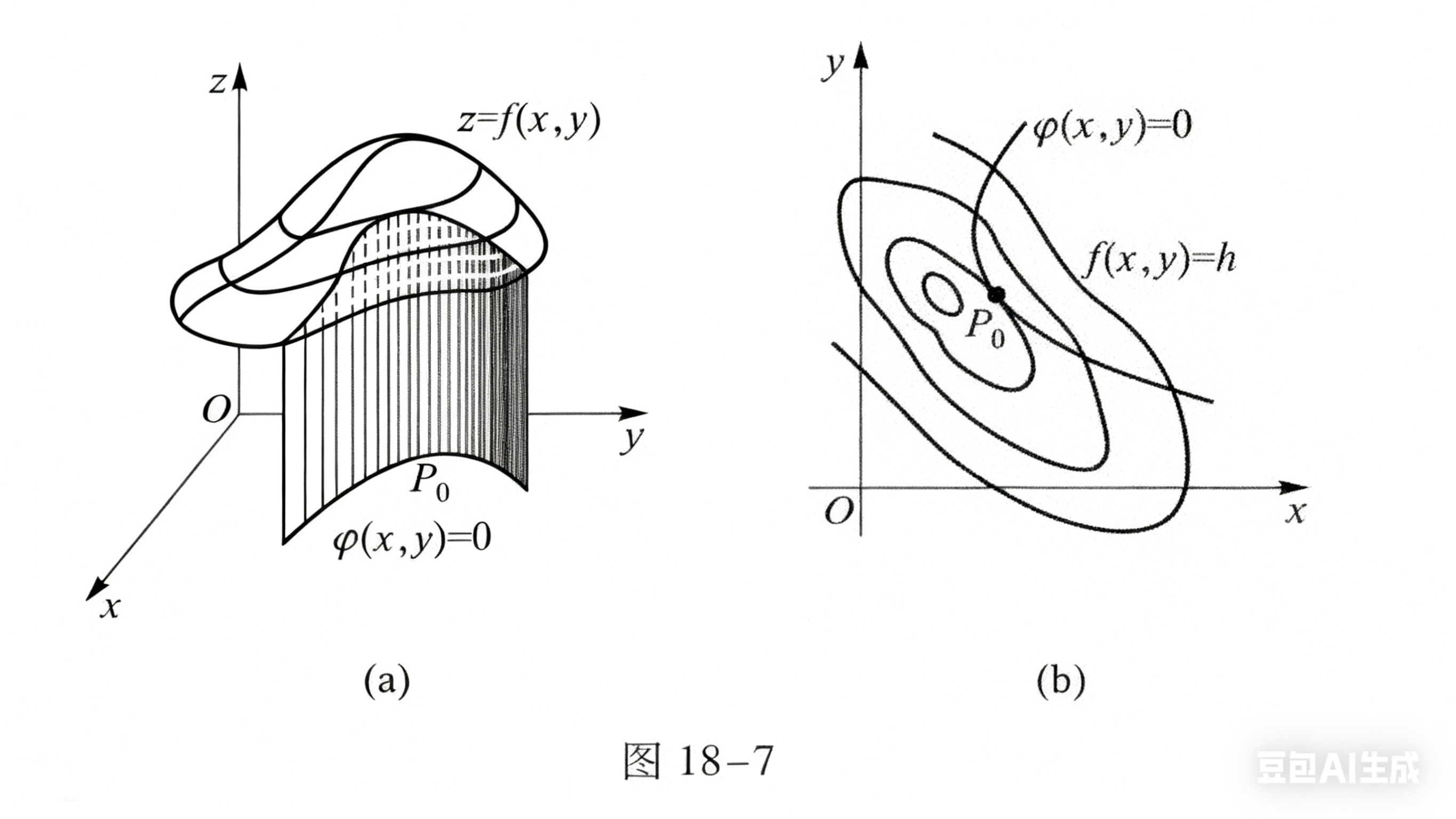
而函数的梯度（∇f\nabla f∇f、∇g\nabla g∇g）正是其等高线（或约束曲线）的法向量。因此，"法向量平行"可转化为数学等式：
∇f(x,y)=λ⋅∇g(x,y)\nabla f(x,y) = \lambda \cdot \nabla g(x,y)∇f(x,y)=λ⋅∇g(x,y)

其中 λ\lambdaλ 就是拉格朗日乘数 （非零常数，用于表示两个梯度的比例关系）。

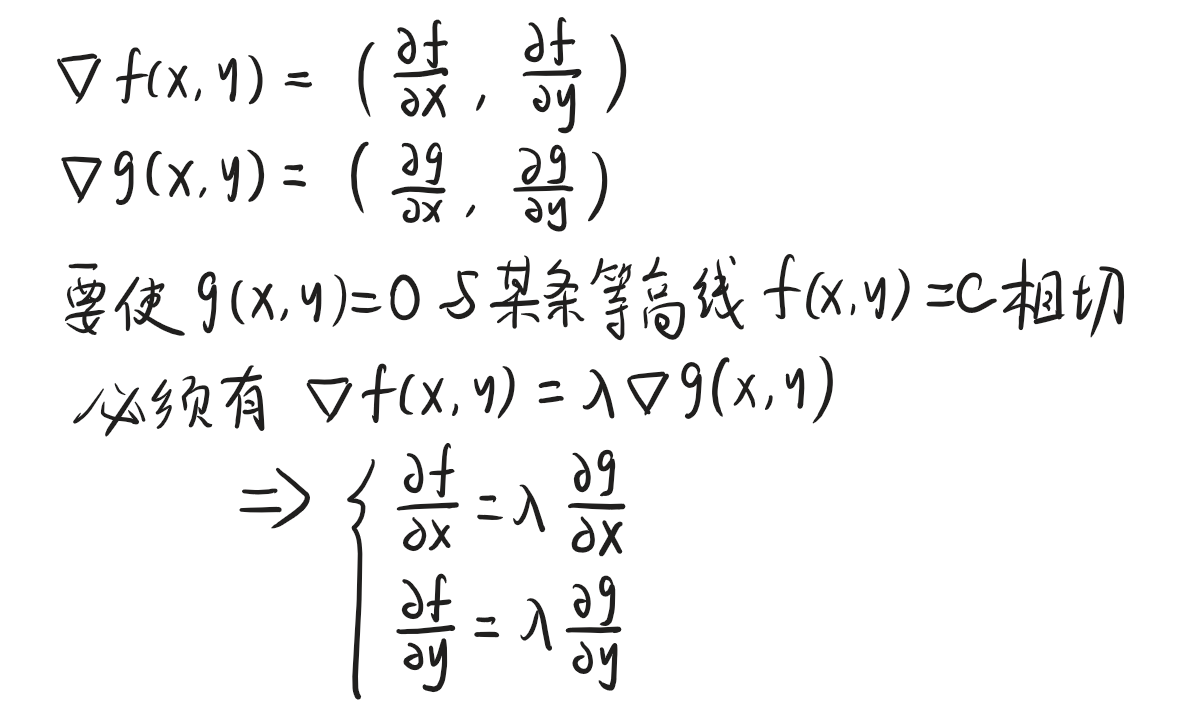
定义拉格朗日函数之后，其实把上面的式子整理整理，就是我们用到的拉格朗日乘数法
2. 拉格朗日函数：将约束问题转化为无约束问题

为了统一求解目标函数和约束条件，我们定义拉格朗日函数 L(x,y,λ)L(x,y,\lambda)L(x,y,λ)：
L(x,y,λ)=f(x,y)−λ⋅g(x,y)L(x,y,\lambda) = f(x,y) - \lambda \cdot g(x,y)L(x,y,λ)=f(x,y)−λ⋅g(x,y)

此时，"原约束问题的极值点"等价于"拉格朗日函数 LLL 关于 x,y,λx,y,\lambdax,y,λ 的无约束极值点"。原因是：

对 LLL 分别求关于 x,y,λx,y,\lambdax,y,λ 的偏导数，并令其等于0，得到的方程组与"梯度平行+约束条件"完全一致：

∂L∂x=∂f∂x−λ⋅∂g∂x=0\frac{\partial L}{\partial x} = \frac{\partial f}{\partial x} - \lambda \cdot \frac{\partial g}{\partial x} = 0∂x∂L=∂x∂f−λ⋅∂x∂g=0 → ∂f∂x=λ⋅∂g∂x\frac{\partial f}{\partial x} = \lambda \cdot \frac{\partial g}{\partial x}∂x∂f=λ⋅∂x∂g
∂L∂y=∂f∂y−λ⋅∂g∂y=0\frac{\partial L}{\partial y} = \frac{\partial f}{\partial y} - \lambda \cdot \frac{\partial g}{\partial y} = 0∂y∂L=∂y∂f−λ⋅∂y∂g=0 → ∂f∂y=λ⋅∂g∂y\frac{\partial f}{\partial y} = \lambda \cdot \frac{\partial g}{\partial y}∂y∂f=λ⋅∂y∂g
∂L∂λ=−g(x,y)=0\frac{\partial L}{\partial \lambda} = -g(x,y) = 0∂λ∂L=−g(x,y)=0 → g(x,y)=0g(x,y) = 0g(x,y)=0（即原约束条件）

3. 推广到多元函数与多个约束

若目标函数为 nnn 元函数 f(x1,x2,...,xn)f(x_1,x_2,...,x_n)f(x1,x2,...,xn)，且存在 kkk 个等式约束 g1(x1,...,xn)=0,g2(x1,...,xn)=0,...,gk(x1,...,xn)=0g_1(x_1,...,x_n)=0, g_2(x_1,...,x_n)=0, ..., g_k(x_1,...,x_n)=0g1(x1,...,xn)=0,g2(x1,...,xn)=0,...,gk(x1,...,xn)=0（k<nk < nk<n，否则约束过多可能无解），则：

需引入 kkk 个拉格朗日乘数 λ1,λ2,...,λk\lambda_1, \lambda_2, ..., \lambda_kλ1,λ2,...,λk；
拉格朗日函数定义为：
L(x1,...,xn,λ1,...,λk)=f(x1,...,xn)−∑i=1kλi⋅gi(x1,...,xn)L(x_1,...,x_n,\lambda_1,...,\lambda_k) = f(x_1,...,x_n) - \sum_{i=1}^k \lambda_i \cdot g_i(x_1,...,x_n)L(x1,...,xn,λ1,...,λk)=f(x1,...,xn)−i=1∑kλi⋅gi(x1,...,xn)
极值点满足的条件：对 LLL 中所有变量（x1,...,xnx_1,...,x_nx1,...,xn 和 λ1,...,λk\lambda_1,...,\lambda_kλ1,...,λk）求偏导，并令其等于0，共 n+kn+kn+k 个方程，可解出 n+kn+kn+k 个未知数。

求函数f(x,y)=∣x∣+∣y∣x2+y2f(x,y)=\frac{|x|+|y|}{\sqrt{x^2+y^2}}f(x,y)=x2+y2 ∣x∣+∣y∣的值域

⭐ 第一步：化到极坐标

设

x=rcos⁡θ,y=rsin⁡θ,r>0 x=r\cos\theta,\qquad y=r\sin\theta, \quad r>0 x=rcosθ,y=rsinθ,r>0

则

∣x∣+∣y∣=r(∣cos⁡θ∣+∣sin⁡θ∣) |x|+|y|=r(|\cos\theta|+|\sin\theta|) ∣x∣+∣y∣=r(∣cosθ∣+∣sinθ∣)

x2+y2=r \sqrt{x^2+y^2}=r x2+y2 =r

所以函数变为仅与角度有关的：

f(θ)=∣cos⁡θ∣+∣sin⁡θ∣ f(\theta)=|\cos\theta|+|\sin\theta| f(θ)=∣cosθ∣+∣sinθ∣

在第一象限（cos⁡θ,sin⁡θ≥0\cos\theta,\sin\theta\ge 0cosθ,sinθ≥0）：

f(θ)=cos⁡θ+sin⁡θ=2 sin⁡(θ+π4) f(\theta)=\cos\theta+\sin\theta = \sqrt{2}\,\sin(\theta+\frac{\pi}{4}) f(θ)=cosθ+sinθ=2 sin(θ+4π)

所以最大值为：

2 \boxed{\sqrt{2}} 2

发生在 θ=π4\theta = \frac{\pi}{4}θ=4π（即 x=y>0x=y>0x=y>0）及其对称方向。

在第一象限的最小值发生在 θ=0\theta=0θ=0 或 θ=π2\theta=\frac{\pi}{2}θ=2π：

f=1 f = 1 f=1

并且由于绝对值对称，其他象限也一样。

最终结论

1 ≤ ∣x∣+∣y∣x2+y2 ≤ 2(x,y≠0) \boxed{1 \;\le\; \frac{|x|+|y|}{\sqrt{x^2+y^2}} \;\le\; \sqrt{2}} \quad (x,y\neq 0) 1≤x2+y2 ∣x∣+∣y∣≤2 (x,y=0)

求曲线Γ:{x2+y2+z2=3x+y−z=1.\Gamma:\quad \begin{cases}x^{2}+y^{2}+z^{2}=3\\[4pt]x+y-z=1.\end{cases}Γ:{x2+y2+z2=3x+y−z=1.上某一点的方向向量

曲线Γ\GammaΓ是两个曲面：

F(x,y,z)=x2+y2+z2−3=0F(x,y,z)=x^{2}+y^{2}+z^{2}-3=0F(x,y,z)=x2+y2+z2−3=0
G(x,y,z)=x+y−z−1=0G(x,y,z)=x+y-z-1=0G(x,y,z)=x+y−z−1=0

的交线。在该交线上的任一点，其切向量方向等于两个曲面在该点的法向量的叉积：

t=∇F×∇G \boxed{\, \mathbf{t}=\nabla F \times \nabla G\, } t=∇F×∇G

因为交线方向同时垂直于两个法向量，因此是法向量叉积。

计算梯度

F(x,y,z)=x2+y2+z2−3 F(x,y,z) = x^2 + y^2 + z^2 - 3 F(x,y,z)=x2+y2+z2−3

∇F=(2x, 2y, 2z) \nabla F = (2x,\;2y,\;2z) ∇F=(2x,2y,2z)

G(x,y,z)=x+y−z−1 G(x,y,z) = x + y - z - 1 G(x,y,z)=x+y−z−1

∇G=(1, 1, −1) \nabla G = (1,\;1,\;-1) ∇G=(1,1,−1)

计算切向量（未单位化）

t=∇F×∇G=(2x,2y,2z)×(1,1,−1) \mathbf{t} = \nabla F \times \nabla G = (2x,2y,2z) \times (1,1,-1) t=∇F×∇G=(2x,2y,2z)×(1,1,−1)

直接算叉积：

t=∣ijk2x2y2z11−1∣ \mathbf{t} =\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2x & 2y & 2z \\ 1 & 1 & -1 \end{vmatrix} t= i2x1j2y1k2z−1

=i(2y⋅(−1)−2z⋅1)−j(2x⋅(−1)−2z⋅1)+k(2x⋅1−2y⋅1) =\mathbf{i}(2y\cdot(-1)-2z\cdot 1) -\mathbf{j}(2x\cdot(-1)-2z\cdot1) +\mathbf{k}(2x\cdot1-2y\cdot1) =i(2y⋅(−1)−2z⋅1)−j(2x⋅(−1)−2z⋅1)+k(2x⋅1−2y⋅1)

简化：

t=(−2y−2z, 2x−2z, 2x−2y) \boxed{ \mathbf{t} = (-2y-2z,\; 2x-2z,\; 2x-2y ) } t=(−2y−2z,2x−2z,2x−2y)

这就是曲线上任一点的 切向量方向。

求在某个指定点 P(x0,y0,z0)P(x_0,y_0,z_0)P(x0,y0,z0) 处的方向向量

只需把坐标代入：

t(P)=(−2y0−2z0, 2x0−2z0, 2x0−2y0) \boxed{ \mathbf{t}(P)=(-2y_0-2z_0,\;2x_0-2z_0,\;2x_0-2y_0) } t(P)=(−2y0−2z0,2x0−2z0,2x0−2y0)