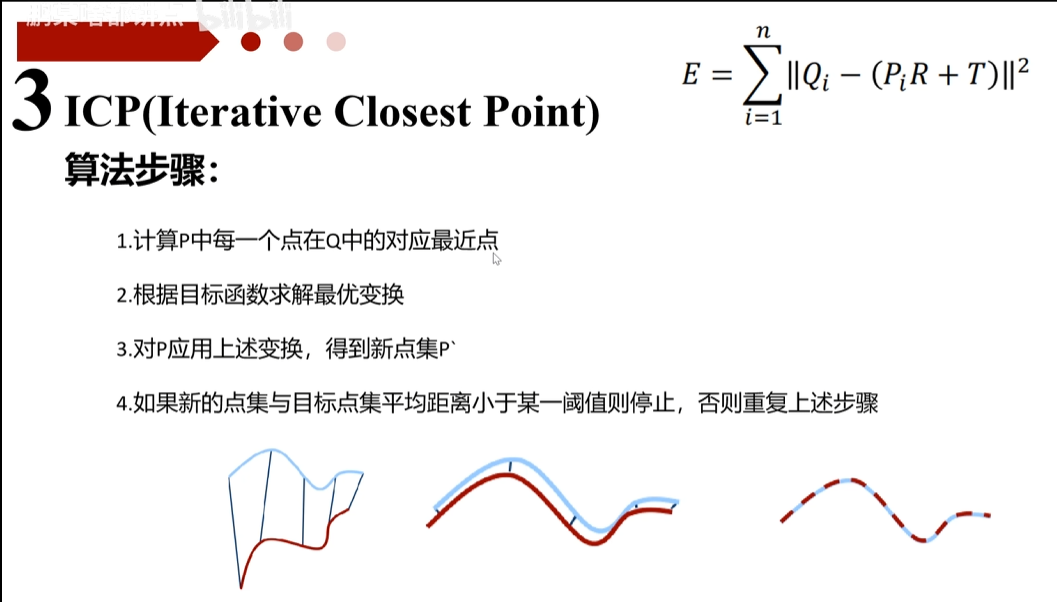
迭代最近点算法ICP(Iterative Closest Point)
一、算法流程:
在带匹配的目标点云P和源点云Q中,按照欧氏距离,找到对应的最邻近点pi∈目标点云P,qi∈目标点云Q。然后计算出最优匹配参数R和t,使得误差函数最小。误差函数为E(R,t)为:
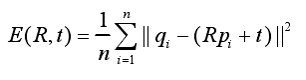
二、公式推导:
步骤 1:计算点云质心,消除平移干扰
将两个点集都以质心点为坐标原点。

步骤 2:代入误差函数,分离旋转与平移

注意上图中第二项中仅与平移相关只是在第一项中确定R的情况下的得到的。是先固定旋转矩阵R,再单独分析平移t的最优解,所以在这个阶段,R被视为已知的 "常数",因此第二项只随t变化。 具体解释如下:

步骤 3:求解最优旋转矩阵R

现在需要求旋转矩阵R和平移矩阵T
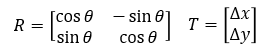
将其带入目标函数E(R)得到关于θ的函数
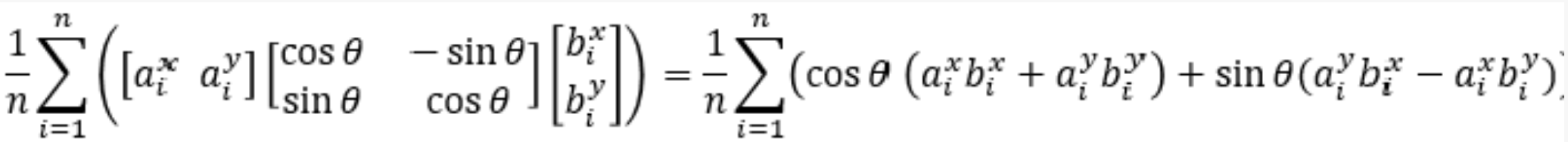
对θ求导,当θ等于0时有极大值。
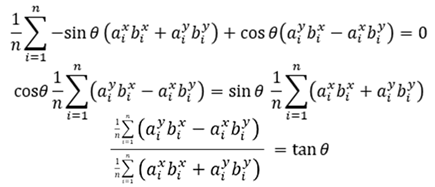
可以求出θ为如下表达式,ai,bi就是点集P和点集Q中的所有点,所以可以求出旋转矩阵的角度θ。
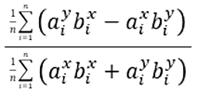
步骤 4:确定平移矩阵t*
由于在步骤二中已经得到平移矩阵的表达式,将求得的旋转矩阵R以及点云质心带入即可。
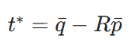
带入后公式为:Amean和Bmean就是点云质心
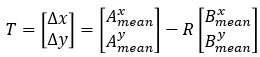
三、优化思路:
1.通过欧氏距离找到的两个点云之间距离最近的点对,实际情况中不一定是真实对应的,这种情况就会拉高计算出的点云之间的距离。可以通过赋予不同的权重来优化。
