MiniRL：用LLM稳定强化学习的新范式与第一阶近似理论

MiniRL：用LLM稳定强化学习的新范式与第一阶近似理论

这篇论文提出了一种新颖的强化学习与大型语言模型结合的理论框架，揭示了何时以及如何通过token级目标函数优化序列级奖励。通过数十万GPU小时的实验验证，论文系统性地分析了训练稳定性关键因素，为MoE模型的RL训练提供了实用指导方案。

论文标题：Stabilizing Reinforcement Learning with LLMs: Formulation and Practices

来源：arXiv:2512.01374v1 [cs.LG] + https://arxiv.org/abs/2512.01374

PS: 整理了LLM、量化投资、机器学习方向的学习资料，关注同名公众号 「 AI极客熊 」 即刻免费解锁

文章核心

研究背景

强化学习已成为提升大型语言模型复杂问题解决能力的关键技术范式，但稳定的训练过程对于成功扩展RL至关重要。由于语言的本质特性，LLM的RL通常采用序列级奖励，即基于完整模型响应分配的标量分数。然而，主流RL算法如REINFORCE和GRPO通常采用token级优化目标。这种奖励分配（序列级）与优化单元（通常为token级）之间的不匹配引发了人们对此类方法合理性和训练稳定性的担忧。特别是，token级优化目标也给MoE模型的RL训练带来了独特挑战，例如动态专家路由机制会使MoE模型中的token级重要性采样比率失效。

研究问题

1. 理论鸿沟：序列级奖励与token级优化目标之间存在根本性不匹配，缺乏理论解释这种做法的合理性
2. 训练不稳定性：MoE模型中的专家路由机制与训练-推理差异、策略陈旧性相互作用，导致训练不稳定甚至崩溃
3. 技术有效性缺失：现有稳定技术（如重要性采样校正、裁剪、Routing Replay）缺乏统一的理论解释，其实际效果存在争议

主要贡献

1. 理论创新：首次提出LLM强化学习的新颖理论框架，将token级优化目标视为序列级奖励的第一阶近似，明确了这种近似成立的关键条件
2. 条件揭示：系统性地揭示了第一阶近似成立的两个必要条件：最小化训练-推理差异和控制策略陈旧性
3. 技术解释：为现有稳定技术提供了统一的理论解释，证明重要性采样校正、裁剪和Routing Replay都是通过维持第一阶近似有效性来稳定训练
4. 实证验证：通过30B MoE模型数十万GPU小时的实验，验证了理论预测并提供了实用的稳定训练配方

方法论精要

理论框架构建

论文的核心理论贡献在于建立了一个连接序列级奖励和token级优化的理论桥梁。研究从真正的序列级奖励目标开始：

J s e q ( θ ) = E x ∼ D , y ∼ π θ ( ⋅ ∣ x ) [ R ( x , y ) ] J_{seq}(\theta) = \mathbb{E}{x \sim D, y \sim \pi\theta(\cdot|x)}[R(x,y)] Jseq(θ)=Ex∼D,y∼πθ(⋅∣x)[R(x,y)]

其中 π θ \pi_\theta πθ是待优化的目标策略， R ( x , y ) R(x,y) R(x,y)是序列级奖励。由于响应通常在推理引擎中采样而非训练引擎，论文采用重要性采样技巧进行转换：

J s e q ( θ ) = E x ∼ D , y ∼ μ θ o l d ( ⋅ ∣ x ) [ π θ ( y ∣ x ) μ θ o l d ( y ∣ x ) R ( x , y ) ] J_{seq}(\theta) = \mathbb{E}{x \sim D, y \sim \mu{\theta_{old}}(\cdot|x)}\left[\frac{\pi_\theta(y|x)}{\mu_{\theta_{old}}(y|x)}R(x,y)\right] Jseq(θ)=Ex∼D,y∼μθold(⋅∣x)[μθold(y∣x)πθ(y∣x)R(x,y)]

然而，该目标的梯度由于序列似然的数值范围大和方差高而难以直接利用。论文的关键洞察是考虑以下替代token级优化目标：

J t o k e n ( θ ) = E x ∼ D , y ∼ μ θ o l d ( ⋅ ∣ x ) [ ∑ t = 1 ∣ y ∣ sg [ π θ ( y t ∣ x , y < t ) μ θ o l d ( y t ∣ x , y < t ) ] R ( x , y ) log ⁡ π θ ( y t ∣ x , y < t ) ] J_{token}(\theta) = \mathbb{E}{x \sim D, y \sim \mu{\theta_{old}}(\cdot|x)}\left[\sum_{t=1}^{|y|} \text{sg}\left[\frac{\pi_\theta(y_t|x,y_{<t})}{\mu_{\theta_{old}}(y_t|x,y_{<t})}\right]R(x,y)\log \pi_\theta(y_t|x,y_{<t})\right] Jtoken(θ)=Ex∼D,y∼μθold(⋅∣x)[∑t=1∣y∣sg[μθold(yt∣x,y<t)πθ(yt∣x,y<t)]R(x,y)logπθ(yt∣x,y<t)]

这实际上就是配备了token级重要性采样权重的REINFORCE算法。论文的核心观点是：可以将这个token级优化目标视为我们真正要优化的序列级目标的第一阶近似。

第一阶近似的成立条件

为了使第一阶近似成立，论文要求目标策略 π θ \pi_\theta πθ和回放策略 μ θ o l d \mu_{\theta_{old}} μθold接近。具体而言，每个token的重要性采样权重可以分解为：

π θ ( y t ∣ x , y < t ) μ θ o l d ( y t ∣ x , y < t ) = π θ o l d ( y t ∣ x , y < t ) μ θ o l d ( y t ∣ x , y < t ) ⏟ 训练-推理差异 × π θ ( y t ∣ x , y < t ) π θ o l d ( y t ∣ x , y < t ) ⏟ 策略陈旧性 \frac{\pi_\theta(y_t|x,y_{<t})}{\mu_{\theta_{old}}(y_t|x,y_{<t})} = \underbrace{\frac{\pi_{\theta_{old}}(y_t|x,y_{<t})}{\mu_{\theta_{old}}(y_t|x,y_{<t})}}{\text{训练-推理差异}} \times \underbrace{\frac{\pi\theta(y_t|x,y_{<t})}{\pi_{\theta_{old}}(y_t|x,y_{<t})}}_{\text{策略陈旧性}} μθold(yt∣x,y<t)πθ(yt∣x,y<t)=训练-推理差异 μθold(yt∣x,y<t)πθold(yt∣x,y<t)×策略陈旧性 πθold(yt∣x,y<t)πθ(yt∣x,y<t)

其中 π θ o l d \pi_{\theta_{old}} πθold表示由训练引擎计算的回放策略，与推理引擎中的 μ θ o l d \mu_{\theta_{old}} μθold不同。因此， π θ \pi_\theta πθ和 μ θ o l d \mu_{\theta_{old}} μθold之间的差距来自两个方面：训练-推理差异和策略陈旧性。

训练-推理差异通常源于训练和推理引擎为获得峰值性能而采用的不同计算内核，即使在同一引擎内，特别是推理端，为了最大化吞吐量通常禁用批量不变内核，导致相同模型输入仍可能获得不同输出。在MoE模型情况下，不一致的专家路由进一步放大了训练-推理差异。

策略陈旧性源于为提高训练效率和计算利用率而做出的权衡。由于RL中的回放阶段通常受生成长度的时间限制，为了通过增加计算资源加速收敛，通常将大批量采样响应分成小批量进行多次梯度更新。因此，较后消费的小批量可能表现出更大的策略陈旧性。

MoE模型挑战与Routing Replay

对于MoE模型，第一阶近似成立的条件变得更为复杂。在生成每个token的前向传递过程中，MoE模型通过专家路由机制动态选择并激活仅一小部分专家参数。论文将MoE模型的token级重要性采样权重表示为：

π θ ( y t ∣ x , y < t ) μ θ o l d ( y t ∣ x , y < t ) = π θ ( y t ∣ x , y < t , e t π ) μ θ o l d ( y t ∣ x , y < t , e μ o l d , t ) = π θ o l d ( y t ∣ x , y < t , e π o l d , t ) μ θ o l d ( y t ∣ x , y < t , e μ o l d , t ) ⏟ 训练-推理差异 × π θ ( y t ∣ x , y < t , e t π ) π θ o l d ( y t ∣ x , y < t , e π o l d , t ) ⏟ 策略陈旧性 \frac{\pi_\theta(y_t|x,y_{<t})}{\mu_{\theta_{old}}(y_t|x,y_{<t})} = \frac{\pi_\theta(y_t|x,y_{<t},e^\pi_t)}{\mu_{\theta_{old}}(y_t|x,y_{<t},e^{\mu_{old},t})} = \underbrace{\frac{\pi_{\theta_{old}}(y_t|x,y_{<t},e^{\pi_{old},t})}{\mu_{\theta_{old}}(y_t|x,y_{<t},e^{\mu_{old},t})}}{\text{训练-推理差异}} \times \underbrace{\frac{\pi\theta(y_t|x,y_{<t},e^\pi_t)}{\pi_{\theta_{old}}(y_t|x,y_{<t},e^{\pi_{old},t})}}_{\text{策略陈旧性}} μθold(yt∣x,y<t)πθ(yt∣x,y<t)=μθold(yt∣x,y<t,eμold,t)πθ(yt∣x,y<t,etπ)=训练-推理差异 μθold(yt∣x,y<t,eμold,t)πθold(yt∣x,y<t,eπold,t)×策略陈旧性 πθold(yt∣x,y<t,eπold,t)πθ(yt∣x,y<t,etπ)

其中 e π e^\pi eπ和 e μ e^\mu eμ分别表示训练和推理引擎中的路由专家，下标"old"对应回放策略。

为解决专家路由对第一阶近似有效性的破坏，论文提出了Routing Replay方法，通过在策略优化期间固定路由专家来稳定MoE模型的RL训练，从而能够像密集模型一样优化模型。具体有两种实现：

1. Vanilla Routing Replay (R2) ：通过在梯度更新期间回放训练引擎中由回放策略确定的路由专家（即 e π o l d , t e^{\pi_{old},t} eπold,t），专注于减轻专家路由对策略陈旧性的影响
2. Rollout Routing Replay (R3) ：通过在训练引擎内统一回放推理引擎中由回放策略确定的路由专家（即 e μ o l d , t e^{\mu_{old},t} eμold,t），旨在减少专家路由对训练-推理差异的影响，同时减轻专家路由对策略陈旧性的影响

MiniRL基准算法

论文提出了MiniRL作为极简基准算法，对REINFORCE优化目标进行了两个最小修改：

1. 群体归一化 ：将原始奖励作为每个响应 y y y的优势估计： A ^ ( x , y ) = R ( x , y ) − E y ∼ μ θ o l d ( ⋅ ∣ x ) [ R ( x , y ) ] \hat{A}(x,y) = R(x,y) - \mathbb{E}{y\sim \mu{\theta_{old}}(\cdot|x)}[R(x,y)] A^(x,y)=R(x,y)−Ey∼μθold(⋅∣x)[R(x,y)]
2. 裁剪机制：采用PPO中的裁剪机制，通过停止某些token的梯度来防止激进策略更新，从而约束策略陈旧性

最终的MiniRL算法目标为：

J M i n i R L ( θ ) = E x ∼ D , y ∼ μ θ o l d ( ⋅ ∣ x ) [ ∑ t = 1 ∣ y ∣ M t ⋅ sg [ π θ ( y t ∣ x , y < t ) μ θ o l d ( y t ∣ x , y < t ) ] A ^ ( x , y ) log ⁡ π θ ( y t ∣ x , y < t ) ] J_{MiniRL}(\theta) = \mathbb{E}{x \sim D, y \sim \mu{\theta_{old}}(\cdot|x)}\left[\sum_{t=1}^{|y|} M_t \cdot \text{sg}\left[\frac{\pi_\theta(y_t|x,y_{<t})}{\mu_{\theta_{old}}(y_t|x,y_{<t})}\right]\hat{A}(x,y)\log \pi_\theta(y_t|x,y_{<t})\right] JMiniRL(θ)=Ex∼D,y∼μθold(⋅∣x)[∑t=1∣y∣Mt⋅sg[μθold(yt∣x,y<t)πθ(yt∣x,y<t)]A^(x,y)logπθ(yt∣x,y<t)]

其中 M t M_t Mt是裁剪函数，基于 π θ ( y t ∣ x , y t ) \pi_\theta(y_t|x,y_{t}) πθ(yt∣x,yt)和 π θ o l d ( y t ∣ x , y t ) \pi_{\theta_{old}}(y_t|x,y_{t}) πθold(yt∣x,yt)的比率决定是否裁剪token y t y_t yt。

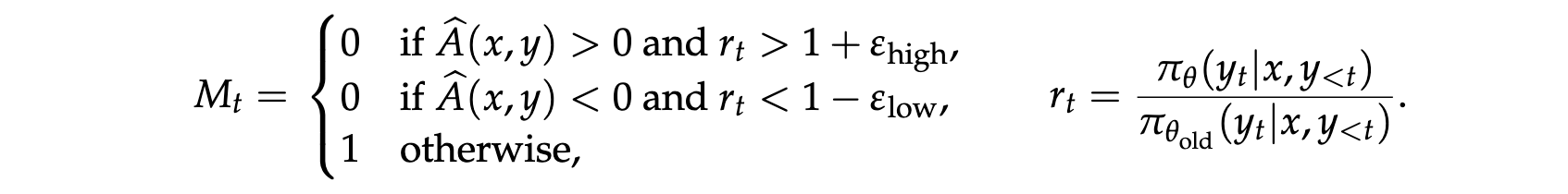
实验洞察

实验设置

论文在数学推理任务上进行实验，模型响应与真实答案比较后分配二元奖励（即 R ( x , y ) ∈ { 0 , 1 } R(x,y) \in \{0,1\} R(x,y)∈{0,1}）。研究整理了4,096个已验证答案的数学问题作为RL训练的提示集。在HMMT25、AIME25和AIME24基准上报告了32个采样响应的平均准确率，每个基准包含30个竞赛级数学问题（共90个）。

实验采用从Qwen3-30B-A3B-Base微调的冷启动模型，采用FP8推理和BF16训练设置，为算法正确性提供了压力测试，其中推理精度低于训练，训练-推理差异较大。除了训练奖励，论文还报告了两个指标的动态变化：(1) 目标策略的token级熵，(2) 推理和训练引擎中回放策略之间的KL散度。

在线策略训练结果

在在线策略训练（全局批量大小等于小批量大小）下，论文验证了token级优化目标底层的第一阶近似有效性是否与训练稳定性相关。实验结果表明：

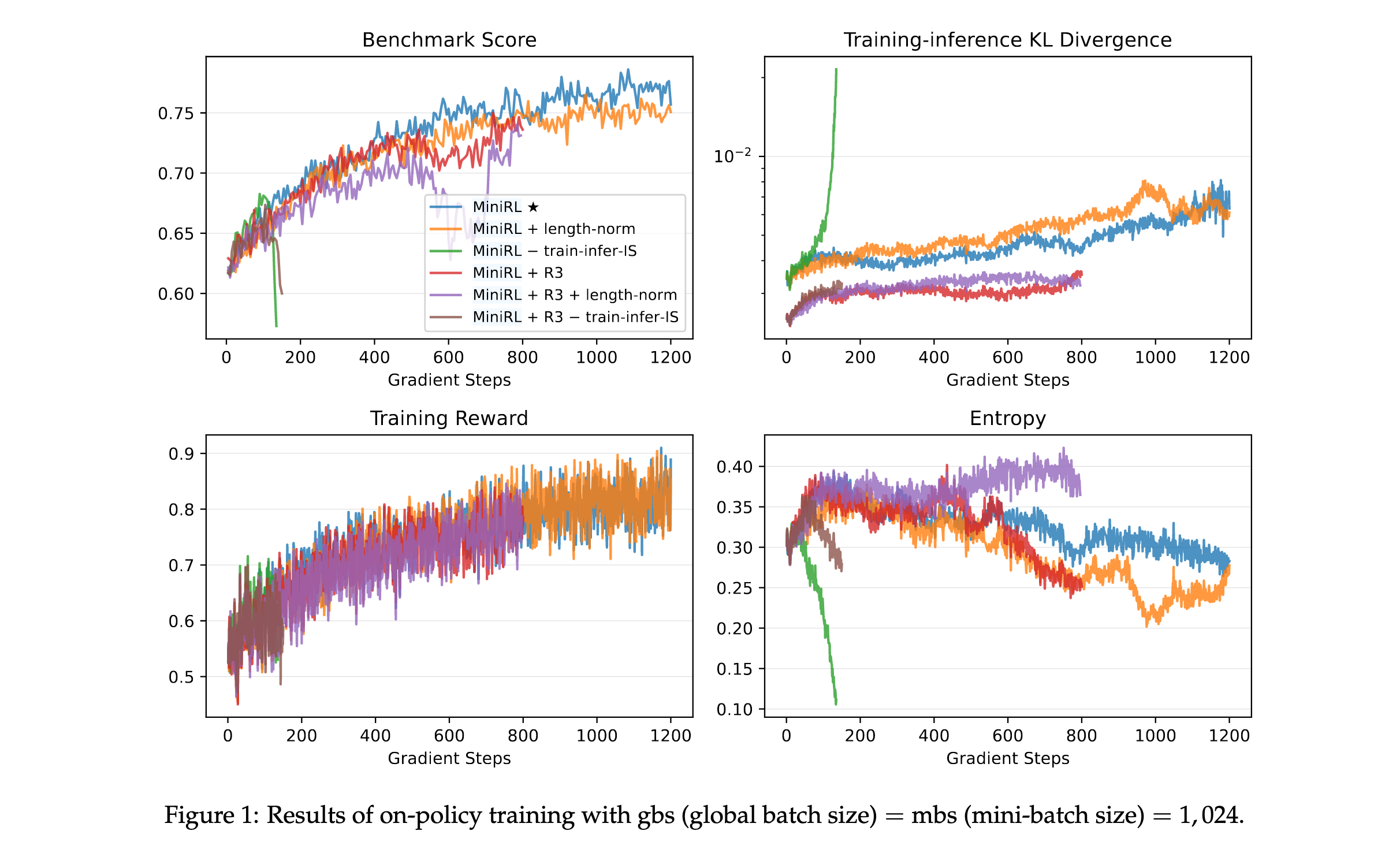
1. MiniRL表现最佳：带有重要性采样校正的基本策略梯度算法实现了最佳性能和训练稳定性
2. 长度归一化损害性能：添加长度归一化导致次优性能，尽管训练保持稳定。这是因为长度归一化使对真实期望序列级奖励的第一阶近似失效，导致有偏的token级优化目标
3. 训练-推理重要性采样至关重要：移除训练-推理重要性采样校正导致训练快速崩溃和熵急剧下降，证实了重要性采样权重是第一阶近似的固有组成部分
4. Routing Replay在在线设置下无效：尽管R3有效减少了训练-推理差异，但在在线策略训练中应用R3并未产生性能提升，甚至与长度归一化结合进一步降低了基准分数

这些结果证明，在设计token级优化目标时，只有那些保持对期望序列级奖励的第一阶近似有效性的目标才能带来改进的训练稳定性和性能。

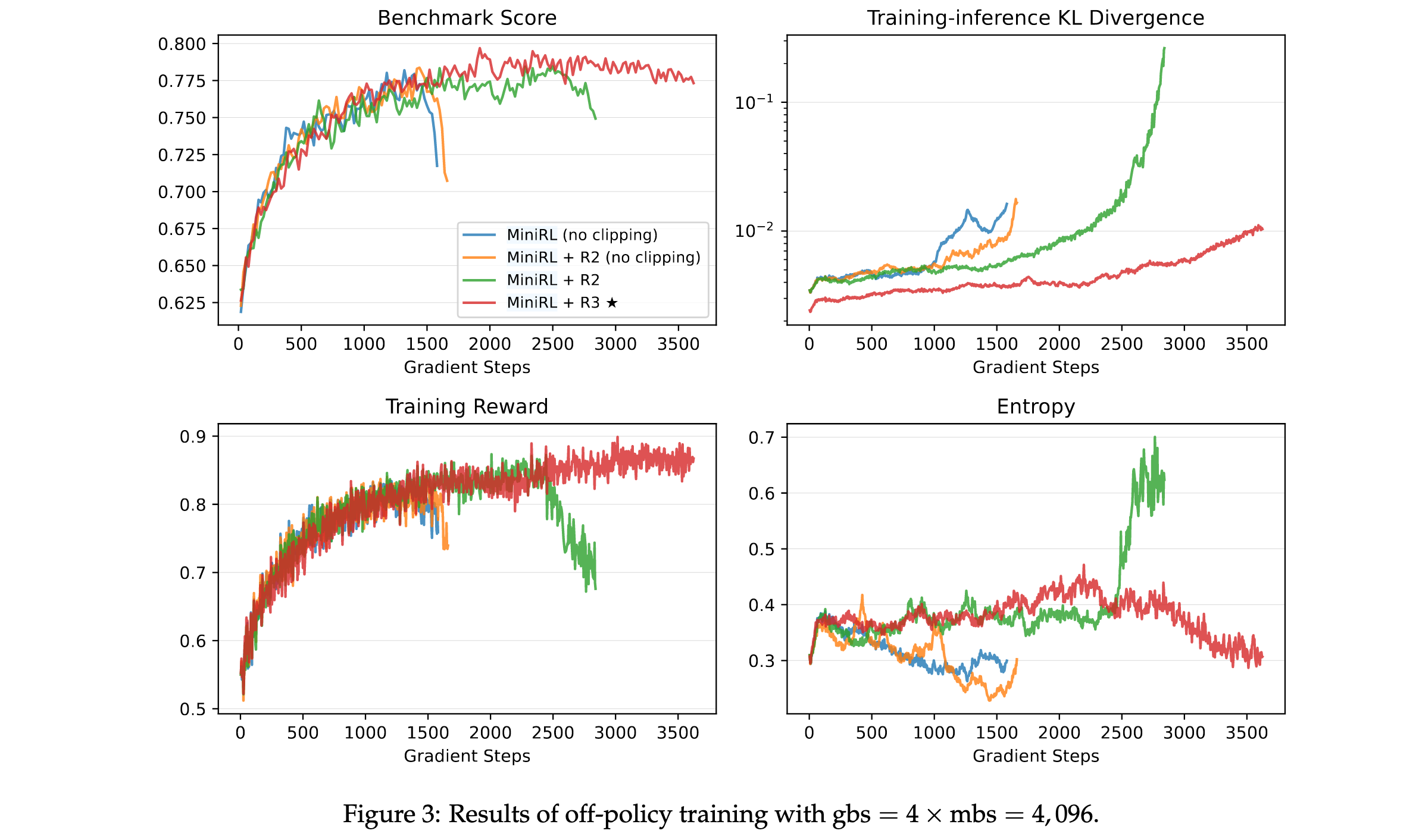
离线策略训练结果

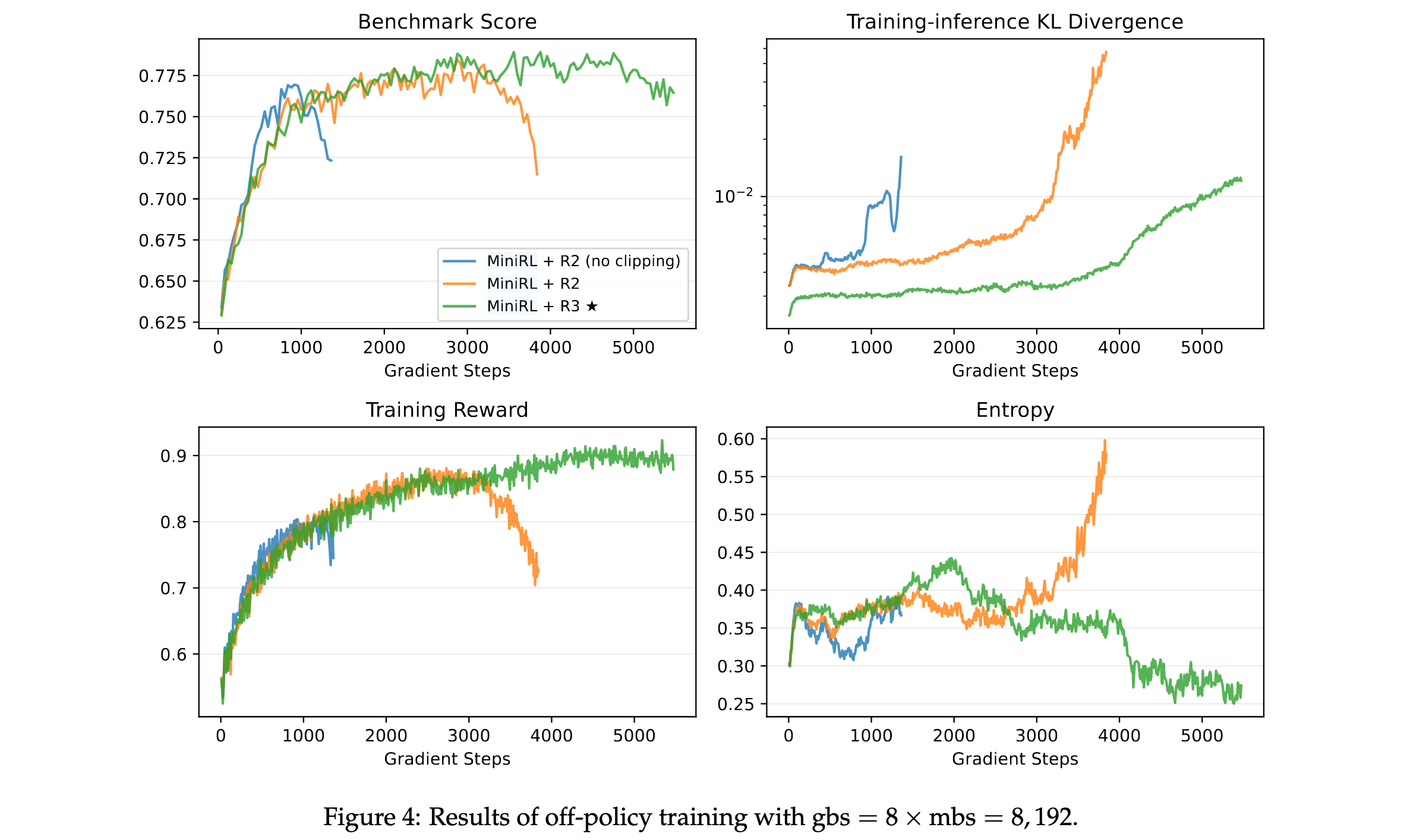
当引入离线策略更新时，Routing Replay和裁剪都成为稳定训练的必要条件。实验表明：

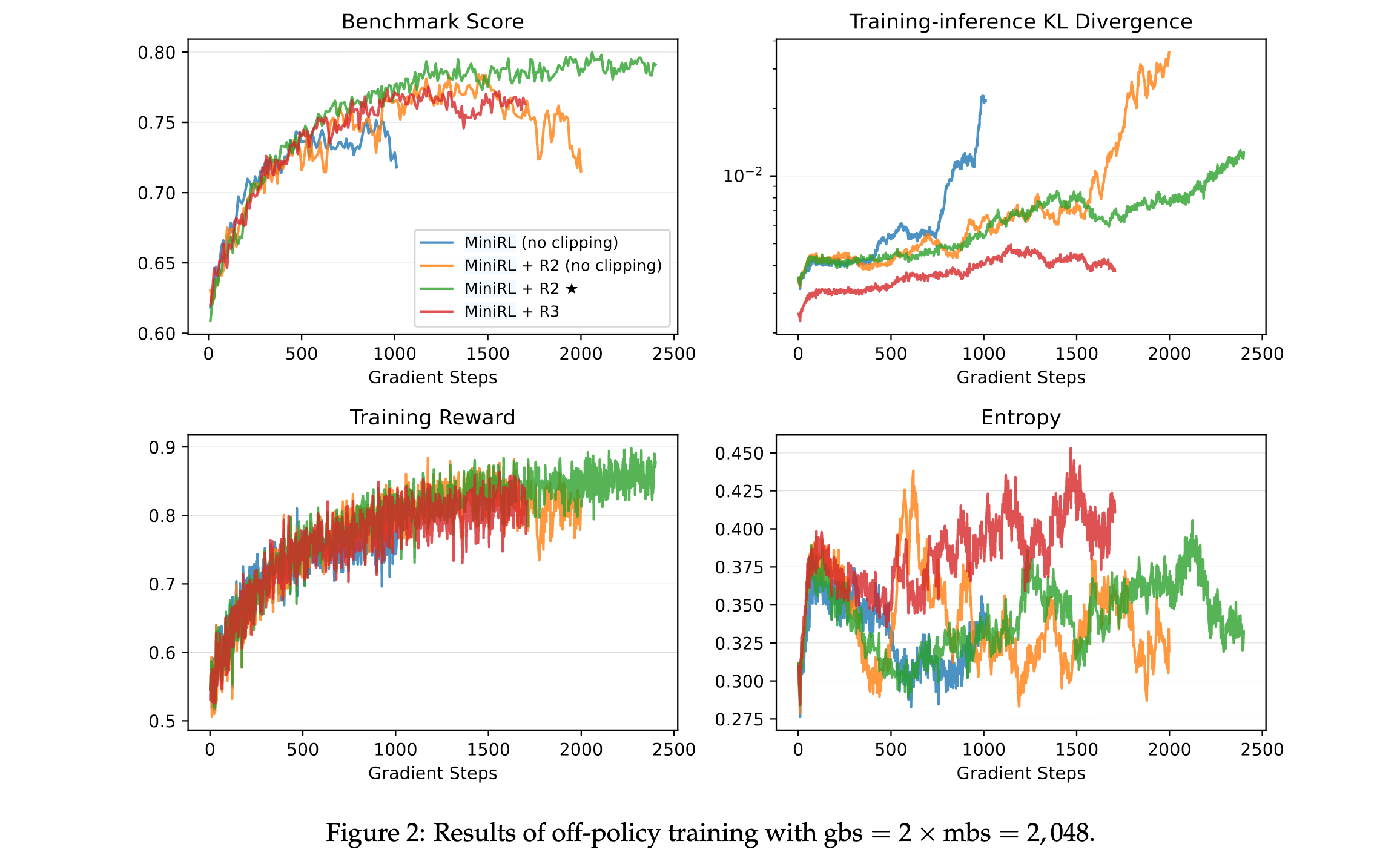
1. 两者缺一不可：省略Routing Replay或裁剪都会导致训练过早崩溃，从而降低峰值性能
2. 离策略程度影响方法选择：当离策略程度较小时（全局批量大小=2×小批量大小），R2优于R3；而当离策略程度较大时（全局批量大小=4×和8×小批量大小），R3超过R2
3. 高离策略下R2失效：在高离策略下，R2无法维持稳定训练，其在训练崩溃前达到的峰值性能也略低于R3

这些发现表明Routing Replay和裁剪对于稳定的离线策略训练是必要的。当离策略程度较小时，R2足以且更有效地稳定MoE模型的RL训练，而在更大离策略程度下，R3变得必要。

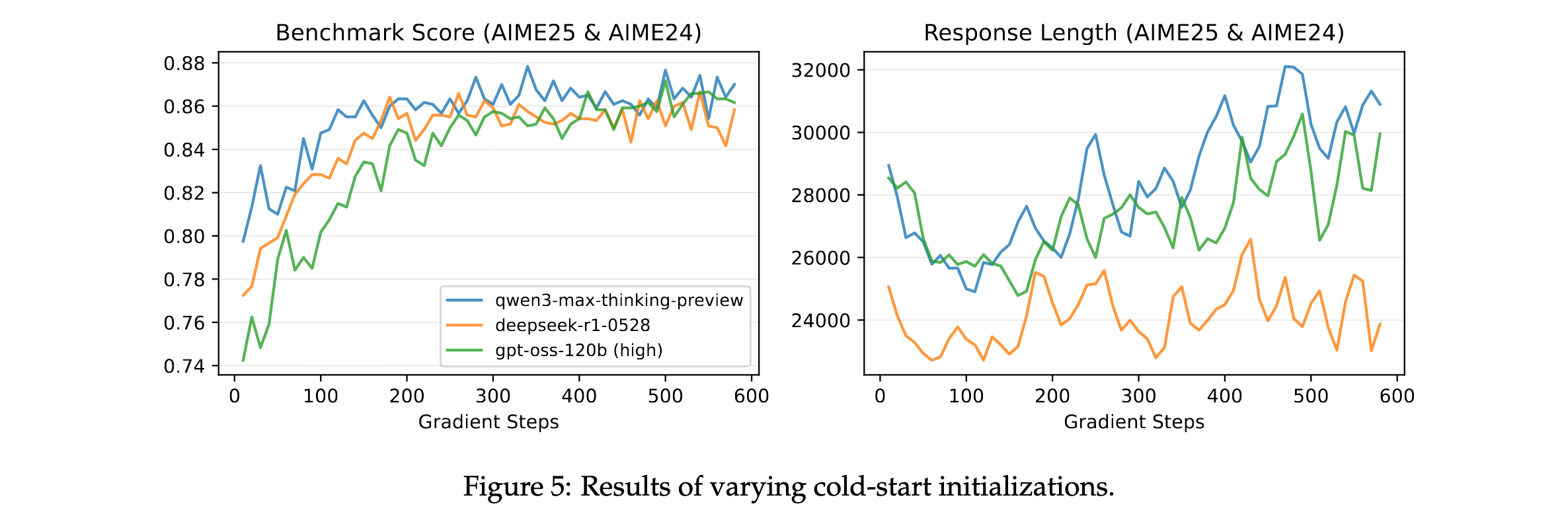
不同冷启动初始化结果

论文调查了使用不同冷启动数据初始化的模型在使用稳定RL配方训练时是否能达到相似性能。比较了从三个前沿模型蒸馏的三个版本冷启动数据：Qwen3-Max-Thinking-Preview、DeepSeek-R1-0528和gpt-oss-120b（高模式）。

结果显示，三个冷启动初始化都达到了可比较的最终性能，这鼓励研究者更加关注RL本身而不是过分关注冷启动初始化的具体细节。此外，在线策略和离线策略训练------一旦稳定------也一致地达到相似的峰值性能。这些结果进一步表明稳定训练在成功扩展RL中起着决定性作用。

理论与实践的统一

论文的实验结果验证了其理论框架的预测：那些保持第一阶近似有效性的技术（如重要性采样校正、裁剪和MoE模型的Routing Replay）都有效地稳定了RL训练。当训练-推理差异和策略陈旧性得到控制时，token级优化目标能够可靠地优化序列级奖励，从而实现稳定的训练过程和一致的性能提升。

这种理论与实践的统一为LLM的RL训练提供了坚实的理论基础，同时也为实践者提供了明确的指导原则：在设计和实施RL算法时，应当优先考虑那些维持第一阶近似有效性的技术选择。