线段树和扫描线结合

扫描线

题目1

1851. 包含每个查询的最小区间 - 力扣（LeetCode）

1.先将查询的数按照大小排序，再将区间按照左边界的大小排序

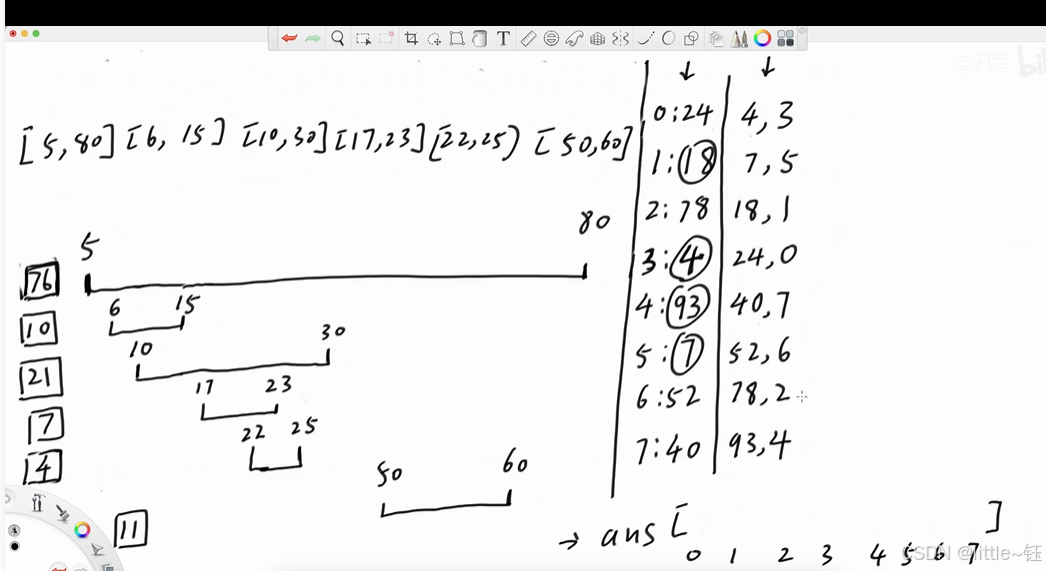
2.先建立一个按照区间大小的排序的小根堆，并且带有其过期的位置。

遍历查询的数，相当于有一根扫描线扫过区间，只要大于开头，就放到小根堆里；然后看堆顶，只要堆顶的元素过期了，就弹出。最后记录堆顶的答案

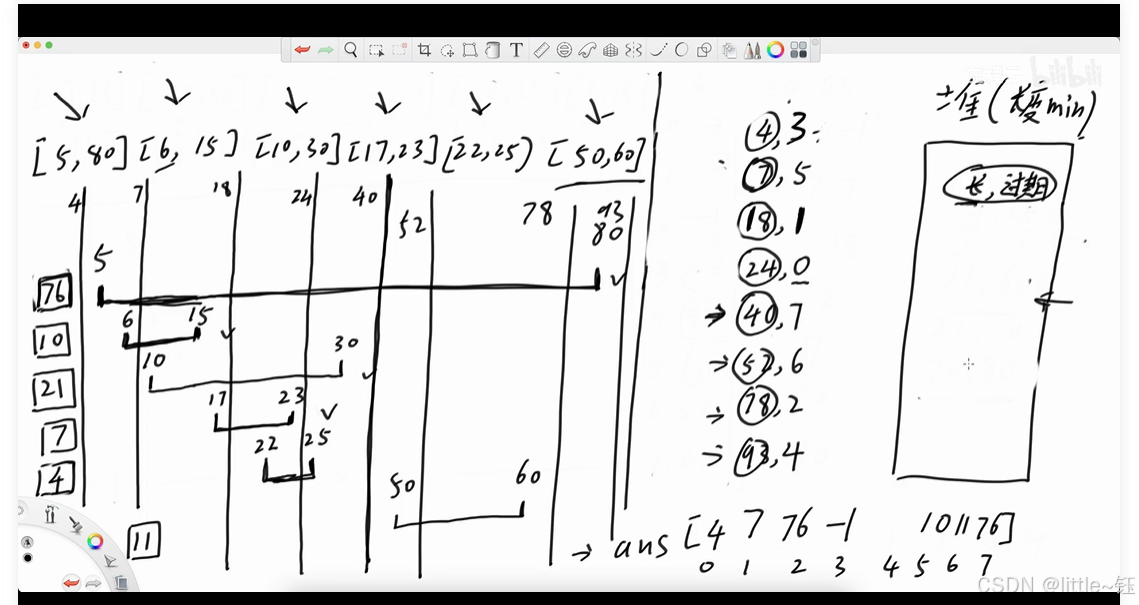
默认堆实现：

java 复制代码

// 包含每个查询的最小区间
// 给你一个二维整数数组intervals，其中intervals[i] = [l, r]
// 表示第i个区间开始于l，结束于r，区间的长度是r-l+1
// 给你一个整数数组queries，queries[i]表示要查询的位置
// 答案是所有包含queries[i]的区间中，最小长度的区间是多长
// 返回数组对应查询的所有答案，如果不存在这样的区间那么答案是-1
// 测试链接 : https://leetcode.cn/problems/minimum-interval-to-include-each-query/
public class Code01_MinimumIntervalQuery1 {

	// 堆结构是现成结构
	public static int[] minInterval(int[][] intervals, int[] queries) {
		int n = intervals.length;
		int m = queries.length;
		Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
		int[][] ques = new int[m][2];
		for (int i = 0; i < m; i++) {
			ques[i][0] = queries[i];
			ques[i][1] = i;
		}
		Arrays.sort(ques, (a, b) -> a[0] - b[0]);
		// 0 : 长度
		// 1 : 影响到的位置
		PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> a[0] - b[0]);
		int[] ans = new int[m];
		for (int i = 0, j = 0; i < m; i++) {
			for (; j < n && intervals[j][0] <= ques[i][0]; j++) {
				heap.add(new int[] { intervals[j][1] - intervals[j][0] + 1, intervals[j][1] });
			}
			while (!heap.isEmpty() && heap.peek()[1] < ques[i][0]) {
				heap.poll();
			}
			if (!heap.isEmpty()) {
				ans[ques[i][1]] = heap.peek()[0];
			} else {
				ans[ques[i][1]] = -1;
			}
		}
		return ans;
	}

}

自定义堆实现：

java 复制代码

// 包含每个查询的最小区间
// 给你一个二维整数数组intervals，其中intervals[i] = [l, r]
// 表示第i个区间开始于l，结束于r，区间的长度是r-l+1
// 给你一个整数数组queries，queries[i]表示要查询的位置
// 答案是所有包含queries[i]的区间中，最小长度的区间是多长
// 返回数组对应查询的所有答案，如果不存在这样的区间那么答案是-1
// 测试链接 : https://leetcode.cn/problems/minimum-interval-to-include-each-query/
public class Code01_MinimumIntervalQuery2 {

	// 堆结构由自己实现
	public static int[] minInterval(int[][] intervals, int[] queries) {
		int n = intervals.length;
		int m = queries.length;
		Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
		int[][] ques = new int[m][2];
		for (int i = 0; i < m; i++) {
			ques[i][0] = queries[i];
			ques[i][1] = i;
		}
		Arrays.sort(ques, (a, b) -> a[0] - b[0]);
		heapSize = 0;
		int[] ans = new int[m];
		for (int i = 0, j = 0; i < m; i++) {
			for (; j < n && intervals[j][0] <= ques[i][0]; j++) {
				push(intervals[j][1] - intervals[j][0] + 1, intervals[j][1]);
			}
			while (!isEmpty() && peekEnd() < ques[i][0]) {
				poll();
			}
			if (!isEmpty()) {
				ans[ques[i][1]] = peekLength();
			} else {
				ans[ques[i][1]] = -1;
			}
		}
		return ans;
	}

	public static int MAXN = 100001;

	public static int[][] heap = new int[MAXN][2];

	public static int heapSize;

	public static boolean isEmpty() {
		return heapSize == 0;
	}

	public static int peekLength() {
		return heap[0][0];
	}

	public static int peekEnd() {
		return heap[0][1];
	}

	public static void push(int h, int e) {
		heap[heapSize][0] = h;
		heap[heapSize][1] = e;
		heapInsert(heapSize++);
	}

	public static void poll() {
		swap(0, --heapSize);
		heapify(0);
	}

	public static void heapInsert(int i) {
		while (heap[i][0] < heap[(i - 1) / 2][0]) {
			swap(i, (i - 1) / 2);
			i = (i - 1) / 2;
		}
	}

	public static void heapify(int i) {
		int l = i * 2 + 1;
		while (l < heapSize) {
			int best = l + 1 < heapSize && heap[l + 1][0] < heap[l][0] ? l + 1 : l;
			best = heap[best][0] < heap[i][0] ? best : i;
			if (best == i) {
				break;
			}
			swap(best, i);
			i = best;
			l = i * 2 + 1;
		}
	}

	public static void swap(int i, int j) {
		int[] tmp = heap[i];
		heap[i] = heap[j];
		heap[j] = tmp;
	}

}

题目2

218. 天际线问题 - 力扣（LeetCode）

1.开区间处理边界问题

2.离散化

java 复制代码

public class Solution {

	// 堆结构是现成结构
	public static List<List<Integer>> getSkyline(int[][] arr) {
		int n = arr.length;
		int m = prepare(arr, n);
		// 0 : 高度
		// 1 : 影响到的位置
		PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> b[0] - a[0]);
		for (int i = 1, j = 0; i <= m; i++) {
			for (; j < n && arr[j][0] <= i; j++) {
				heap.add(new int[] { arr[j][2], arr[j][1] });
			}
			while (!heap.isEmpty() && heap.peek()[1] < i) {
				heap.poll();
			}
			if (!heap.isEmpty()) {
				height[i] = heap.peek()[0];
			}
		}
		List<List<Integer>> ans = new ArrayList<>();
		for (int i = 1, pre = 0; i <= m; i++) {
			if (pre != height[i]) {
				ans.add(Arrays.asList(xsort[i], height[i]));
			}
			pre = height[i];
		}
		return ans;
	}

	public static int MAXN = 100001;

	public static int[] xsort = new int[MAXN];

	public static int[] height = new int[MAXN];

	// 准备工作如下
	// 1) 收集大楼左边界、右边界-1、右边界的值
	// 2) 收集的所有值排序、去重
	// 3) 大楼的左边界和右边界，修改成排名值
	// 4) 大楼根据左边界排序
	// 5) 清空height数组
	// 6) 返回离散值的个数
	public static int prepare(int[][] arr, int n) {
		int size = 0;
		// 大楼的左边界、右边界-1、右边界，三个值都去离散化
		for (int i = 0; i < n; i++) {
			xsort[++size] = arr[i][0];
			xsort[++size] = arr[i][1] - 1;
			xsort[++size] = arr[i][1];
		}
		Arrays.sort(xsort, 1, size + 1);
		// 排序之后去重，去重后的数值有m个
		int m = 1;
		for (int i = 1; i <= size; i++) {
			if (xsort[m] != xsort[i]) {
				xsort[++m] = xsort[i];
			}
		}
		// 修改大楼影响到的左右边界，都变成排名值
		for (int i = 0; i < n; i++) {
			arr[i][0] = rank(m, arr[i][0]);
			// 大楼影响到的右边界，减少1！
			// 课上重点说明的内容
			arr[i][1] = rank(m, arr[i][1] - 1);
		}
		// 所有大楼根据左边界排序
		Arrays.sort(arr, 0, n, (a, b) -> a[0] - b[0]);
		// 高度数组清空
		Arrays.fill(height, 1, m + 1, 0);
		// 返回有多少个不同的离散值
		return m;
	}

	// 查询数值v的排名(离散值)
	public static int rank(int n, int v) {
		int ans = 0;
		int l = 1, r = n, mid;
		while (l <= r) {
			mid = (l + r) >> 1;
			if (xsort[mid] >= v) {
				ans = mid;
				r = mid - 1;
			} else {
				l = mid + 1;
			}
		}
		return ans;
	}

}

扫描线+线段树
题目1

1.求矩形的面积和，不包过重叠的面积

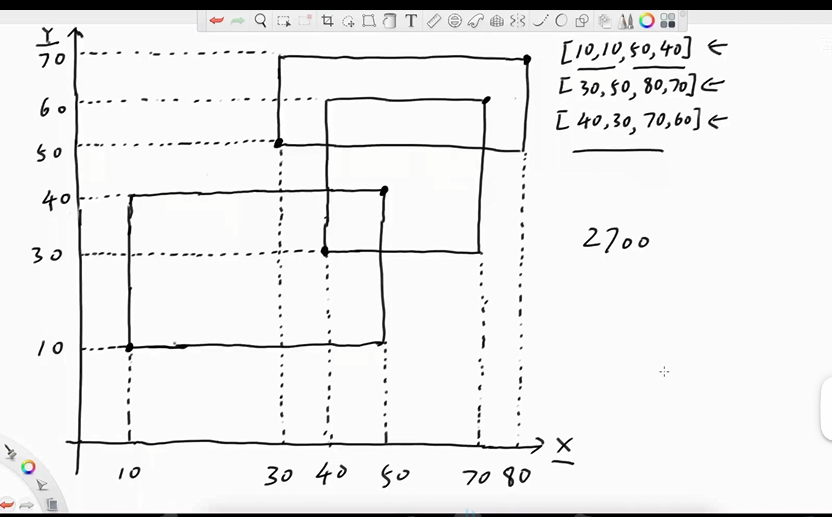
2.以上面的例题为例，按左边界增1，有边界减1，得到6个事件

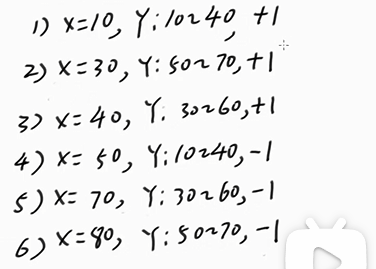
3.扫描线首先来到10，没有产生面积，10-40加1；然后扫到30，产生面积为10-70的覆盖长度乘以20；后面扫到的位置同样方法处理，用10-70的覆盖长度乘以此时的边界和上个边界的距离，然后左边界有加1，右边界就减1

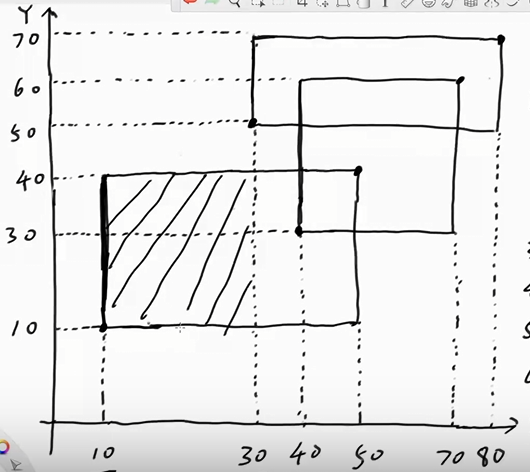
4.预处理：把y值离散化；离散化后，如果一个矩形边界为离散化的编号为x~y，那就在x~y-1这段线段上加1或减1。

维护好总长度，覆盖长度，覆盖的次数(全覆盖)这三个信息。为了维护好总长度，要额外增加一个9:3100，

因为线段树上x~y的总长度就等于离散化后的编号(y+1)对应的原坐标减x对应的原坐标

P5490 【模板】扫描线 & 矩形面积并 - 洛谷