一、算法简介
QSMODE (Q-Spline Multi-Operator Differential Evolution,Q-样条多算子差分进化算法)是一种面向自动驾驶系统(ADS)路径规划问题的强化学习增强型元启发式优化算法。
核心定位
- 算法类型:基于种群的进化算法 + 强化学习(Q-learning)混合框架
- 核心功能 :在复杂环境中生成从起点到终点的安全、平滑、最优路径
- 关键创新:将强化学习从传统的"参数调节工具"提升为"路径生成器",直接利用学习经验生成高质量路径
名称解析
| 组成部分 | 含义 |
|---|---|
| Q | Q-learning(Q学习),经典强化学习方法 |
| S | Spline(样条),三次样条插值平滑技术 |
| MODE | Multi-Operator Differential Evolution(多算子差分进化),基础优化框架 |
二、算法原理
2.1 问题建模:马尔可夫决策过程(MDP)
QSMODE将路径规划建模为马尔可夫决策过程 ,定义三元组 ( S , A , R ) (S, A, R) (S,A,R):
状态空间 S S S
状态表示车辆在环境中的位置:
S = { ( x i , y j ) ∣ x i = x m i n + i ⋅ x r e s , y j = y m i n + j ⋅ y r e s } i = 1 , j = 1 i = n c x , j = n c y S = \{(x_i, y_j) \mid x_i = x_{min} + i \cdot x_{res},\ y_j = y_{min} + j \cdot y_{res}\}{i=1,j=1}^{i=n{cx},j=n_{cy}} S={(xi,yj)∣xi=xmin+i⋅xres, yj=ymin+j⋅yres}i=1,j=1i=ncx,j=ncy
- 将连续搜索空间离散化为网格
- 每个网格单元对应一个唯一状态
- 分辨率 ( x r e s , y r e s ) (x_{res}, y_{res}) (xres,yres) 控制状态粒度
动作空间 A A A
动作表示车辆的离散转向角度 :
A = { θ i = i ⋅ 360 ° n a } i = 1 n a A = \left\{\theta_i = \frac{i \cdot 360°}{n_a}\right\}_{i=1}^{n_a} A={θi=nai⋅360°}i=1na
- n a n_a na:可选动作数量(通常设为8,即45°间隔)
- 每个动作 θ i \theta_i θi 指定车辆从当前状态转移到下一状态的运动方向
奖励函数 R ( s , a ) R(s,a) R(s,a)
r ( s , a ) = − ( d ( s n , s t ) + p T ( s , a ) ) r(s,a) = -\left(d(s^n, s_t) + p^T(s,a)\right) r(s,a)=−(d(sn,st)+pT(s,a))
| 组件 | 说明 |
|---|---|
| d ( s n , s t ) d(s^n, s_t) d(sn,st) | 下一状态 s n s^n sn 到目标点 s t s_t st 的欧氏距离 |
| p T ( s , a ) p^T(s,a) pT(s,a) | 总碰撞惩罚(点惩罚 + 线段惩罚) |
| 负号 | 将最小化问题转化为最大化奖励问题 |
2.2 Q-learning核心机制
Q表结构
- 二维矩阵 :行对应状态 s = ( x , y ) s=(x,y) s=(x,y),列对应动作 a = θ a=\theta a=θ
- 存储内容 : Q ( s , a ) Q(s,a) Q(s,a) 表示在状态 s s s 执行动作 a a a 的长期期望回报
Q值更新规则
Q ( s , a ) ← Q ( s , a ) + α [ r + γ max a n Q ( s n , a n ) − Q ( s , a ) ] Q(s,a) \leftarrow Q(s,a) + \alpha\left[r + \gamma \max_{a^n}Q(s^n,a^n) - Q(s,a)\right] Q(s,a)←Q(s,a)+α[r+γanmaxQ(sn,an)−Q(s,a)]
| 参数 | 含义 | 典型值 |
|---|---|---|
| α \alpha α | 学习率 | 0.6 |
| γ \gamma γ | 折扣因子 | 0.9 |
| r r r | 即时奖励 | 由奖励函数计算 |
| max a n Q ( s n , a n ) \max_{a^n}Q(s^n,a^n) maxanQ(sn,an) | 下一状态最大Q值 | 未来期望回报 |
2.3 双模式更新机制
QSMODE创新性地提出两种Q表更新模式,通过自适应概率切换:
模式1:探索模式(Exploration)
- 触发条件 :随机数 < P r l < P_{rl} <Prl(随迭代递减的概率)
- 核心操作 :在当前状态随机选择动作 a ∈ A a \in A a∈A
- 目的:探索未知状态空间,增强种群多样性,避免局部最优
- 执行过程 :
- 从起点开始设置当前状态 s s s
- 随机选择动作 a a a
- 计算下一状态 s n s^n sn 和奖励 r r r
- 更新Q表
- 将 s n s^n sn 设为当前状态,重复直到达到最大迭代次数 C 1 m a x C1_{max} C1max
模式2:利用模式(Exploitation)
- 触发条件 :随机数 ≥ P r l \geq P_{rl} ≥Prl
- 核心操作:利用进化算法生成的优质路径训练Q表
- 目的:利用已有经验加速收敛,强化对优质解的学习
- 执行过程 :
- 遍历种群中的每个路径
- 对路径中的每对相邻航点 ( s , s n ) (s, s^n) (s,sn):
- 计算动作角度: θ r = tan − 1 ( y n − y r x n − x r ) \theta_r = \tan^{-1}\left(\frac{y_n-y_r}{x_n-x_r}\right) θr=tan−1(xn−xryn−yr)
- 评估奖励 r ( s , a ) r(s,a) r(s,a)
- 更新Q表
2.4 自适应切换概率 P r l P_{rl} Prl
P r l t = P r l , m i n + ( P r l , i n i t − P r l , m i n ) ( 1 − t m a x _ i t e r ) P_{rl}^t = P_{rl,min} + (P_{rl,init} - P_{rl,min})\left(1 - \frac{t}{max\_iter}\right) Prlt=Prl,min+(Prl,init−Prl,min)(1−max_itert)
- 线性衰减 :从初始值 P r l , i n i t = 0.5 P_{rl,init}=0.5 Prl,init=0.5 递减至最小值 P r l , m i n = 0 P_{rl,min}=0 Prl,min=0
- 动态平衡:早期侧重探索,后期侧重利用
- 保证收敛 :即使 P r l , m i n = 0 P_{rl,min}=0 Prl,min=0,仍通过进化算子维持种群多样性
2.5 三次样条插值平滑
核心思想
进化算法生成的路径由离散航点组成,在狭窄通道和急转弯处可能出现路径尖锐 问题。三次样条插值在保持路径形状的同时生成连续可导的平滑曲线。
数学表达
将路径分为两组线段:
主段(Main Segments):连接原始航点
- 参数 T ∈ [ 0 , 1 ] T \in [0,1] T∈[0,1],分为 n d − 1 n_d-1 nd−1 个区间
- t i ∈ [ i − 1 n d − 1 , i n d − 1 ] t_i \in \left[\frac{i-1}{n_d-1}, \frac{i}{n_d-1}\right] ti∈[nd−1i−1,nd−1i]
次段(Secondary Segments):样条插值点
- 参数 K ∈ [ 0 , 1 ] K \in [0,1] K∈[0,1],分为 n s − 1 n_s-1 ns−1 个区间
- k i ∈ [ i − 1 n s − 1 , i n s − 1 ] k_i \in \left[\frac{i-1}{n_s-1}, \frac{i}{n_s-1}\right] ki∈[ns−1i−1,ns−1i]
三次样条多项式 (第 i i i 段):
S i ( k ) = a i ( k − k i ) 3 + b i ( k − k i ) 2 + c i ( k − k i ) + d i S_i(k) = a_i(k-k_i)^3 + b_i(k-k_i)^2 + c_i(k-k_i) + d_i Si(k)=ai(k−ki)3+bi(k−ki)2+ci(k−ki)+di
其中 ( a i , b i , c i , d i ) (a_i, b_i, c_i, d_i) (ai,bi,ci,di) 为系数,通过求解三对角方程组确定,保证:
- 路径连续性
- 一阶导数连续(切线方向平滑)
- 二阶导数连续(曲率变化平滑)
三、算法步骤
步骤1:初始化阶段
输入:起点(xs,ys),终点(xt,yt),障碍物信息,算法参数
输出:初始种群P,初始Q表
1. 设置算法参数:
- 种群大小 npop = 30
- 最大迭代次数 max_iter = 500
- 学习率 α = 0.6,折扣因子 γ = 0.9
- 切换概率 Prl_init = 0.5,Prl_min = 0
- 网格分辨率 xres = yres = 0.15
- 动作数量 na = 8
- 最大样条点数 ns = 100
2. 确定问题维度(航点数量):
nd = max(round(β × nobst), 1)
其中 β = 1(航点率),nobst为障碍物数量
3. 生成初始种群P:
每个个体Ii表示一条候选路径
Ii = {(xj^i, yj^i)}j=1^nd,包含nd个航点坐标对
4. 初始化Q表:
Q(s,a) = 0,对所有状态s和动作a步骤2:进化优化阶段(标准MODE操作)
输入:当前种群P
输出:变异、交叉后的新种群
1. 变异操作(Mutation):
应用多种变异策略生成变异向量
- DE/rand/1
- DE/best/1
- DE/current-to-best/1
2. 交叉操作(Crossover):
二项式交叉或指数交叉
生成试验向量
3. 选择操作(Selection):
一对一贪婪选择
保留更优个体进入下一代步骤3:强化学习路径生成
输入:当前Q表,起点(xs,ys),终点(xt,yt)
输出:RL生成的候选路径path_rl
函数 GeneratePathByRL():
1. 初始化:s = (xs,ys),path_rl = [s]
2. WHILE 未达到终止条件(C2_max = 500)DO:
a. 动作选择(QSMODE使用Q表):
a* = argmax_{a∈A} Q(s,a)
对应转向角度 θr = θ_a*
b. 状态转移:
xn = xr + cos(θr) × step_size
yn = yr + sin(θr) × step_size
sn = (xn, yn)
c. 终止判断:
IF 到达目标点 THEN
返回 path_rl
ELSE IF sn 超出边界 THEN
终止,返回无效路径
ELSE
将sn加入path_rl
s ← sn
ENDIF
3. 返回 path_rl(或"无路径")步骤4:路径评估与种群更新
输入:RL生成的路径path_rl,当前种群P
输出:更新后的种群P
1. 计算路径代价(式2):
cost = L × (1 + β × p^T)
其中:
- L = Σ√[(xi+1-xi)² + (yi+1-yi)²] (路径长度)
- p^T = (1/B)Σ[Σpi^b + Σpline,j^b] (平均碰撞惩罚)
- β = 100(安全权重)
2. 比较与替换:
找出种群中最差个体(最大代价)
IF cost(path_rl) < cost(worst) THEN
用path_rl替换worst
ENDIF
3. 更新全局最优路径gbest步骤5:路径平滑
输入:全局最优路径gbest
输出:平滑后的路径gbest_smooth
1. 提取gbest的nd个航点作为样条节点
2. 构建三次样条插值:
- 计算每个区间的系数(ai, bi, ci, di)
- 求解三对角线性方程组保证二阶连续
3. 生成ns个均匀分布的样条点
4. 输出平滑路径gbest_smooth步骤6:Q表更新(双模式)
输入:当前种群P,当前Q表,当前迭代t
输出:更新后的Q表
1. 更新切换概率:
Prl = 0.5 × (1 - t/max_iter)
2. 生成随机数 r ∈ [0,1]
3. IF r < Prl THEN
// 模式1:探索
执行探索模式更新(算法2,第4-20行)
- 从起点开始
- 随机选择动作
- 模拟路径并更新Q表
- 重复C1_max = 20次
ELSE
// 模式2:利用
执行利用模式更新(算法2,第22-40行)
- 遍历种群中每个路径
- 对每对相邻航点计算动作角度
- 评估奖励并更新Q表
ENDIF
4. 返回更新后的Q表四、路径规划部分结果
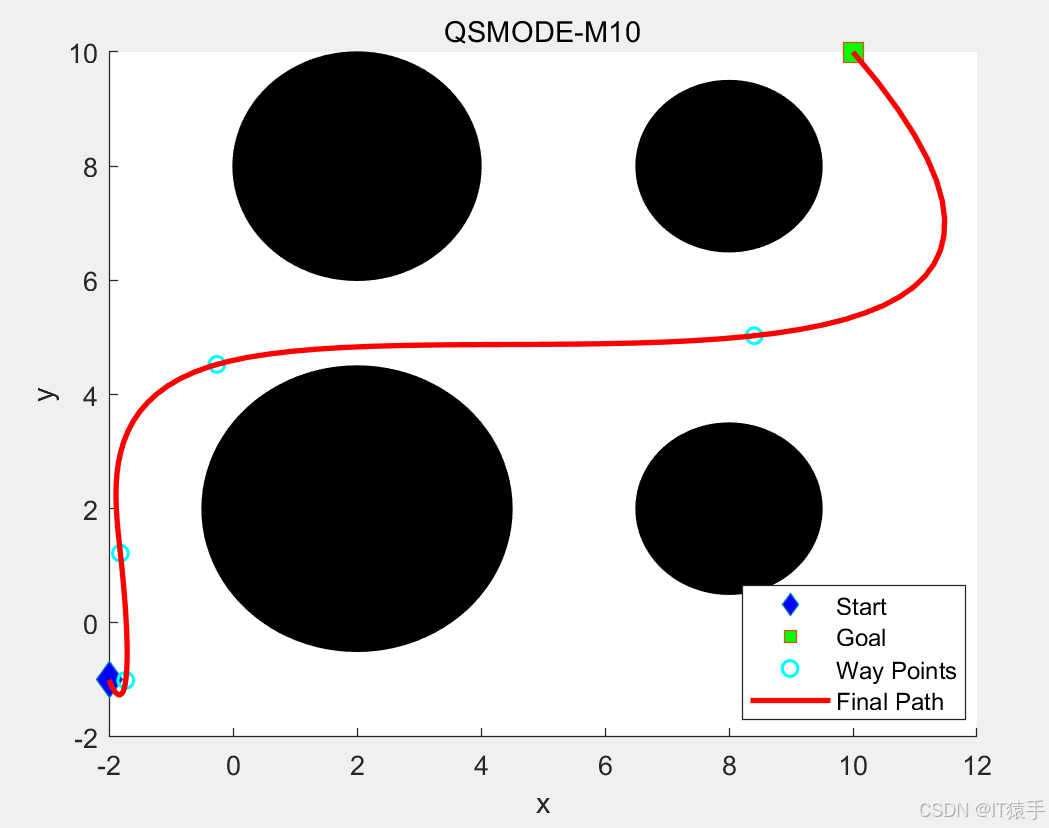
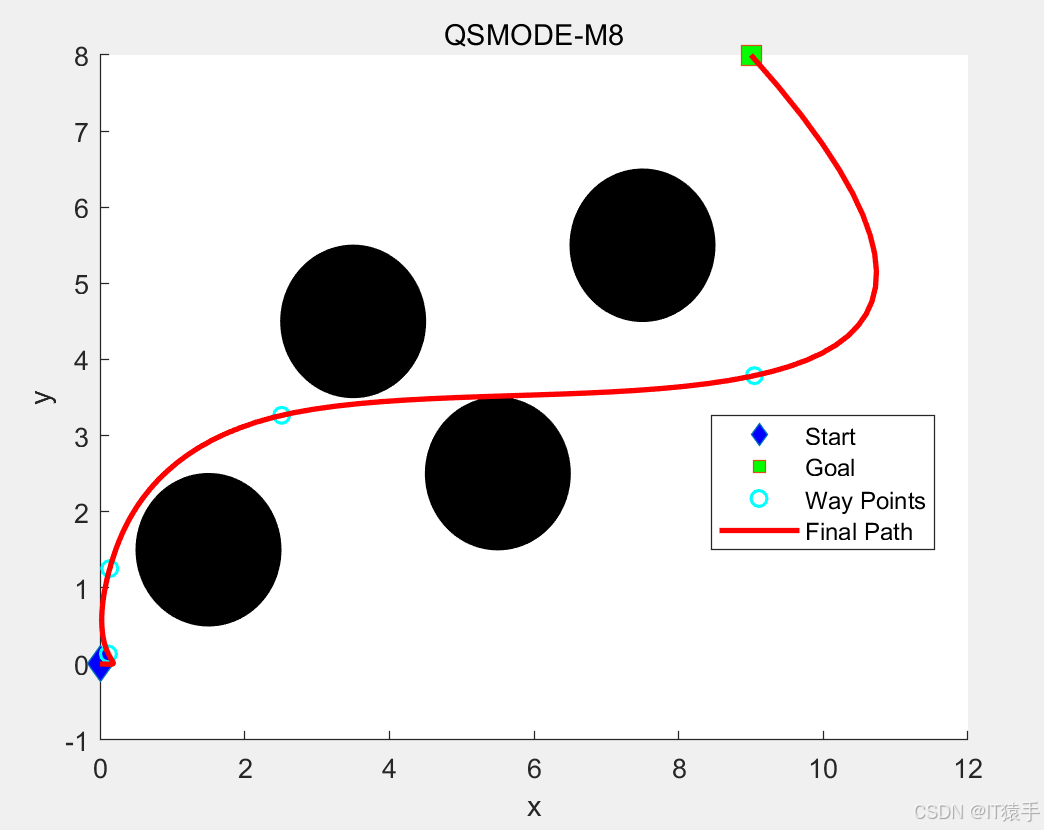
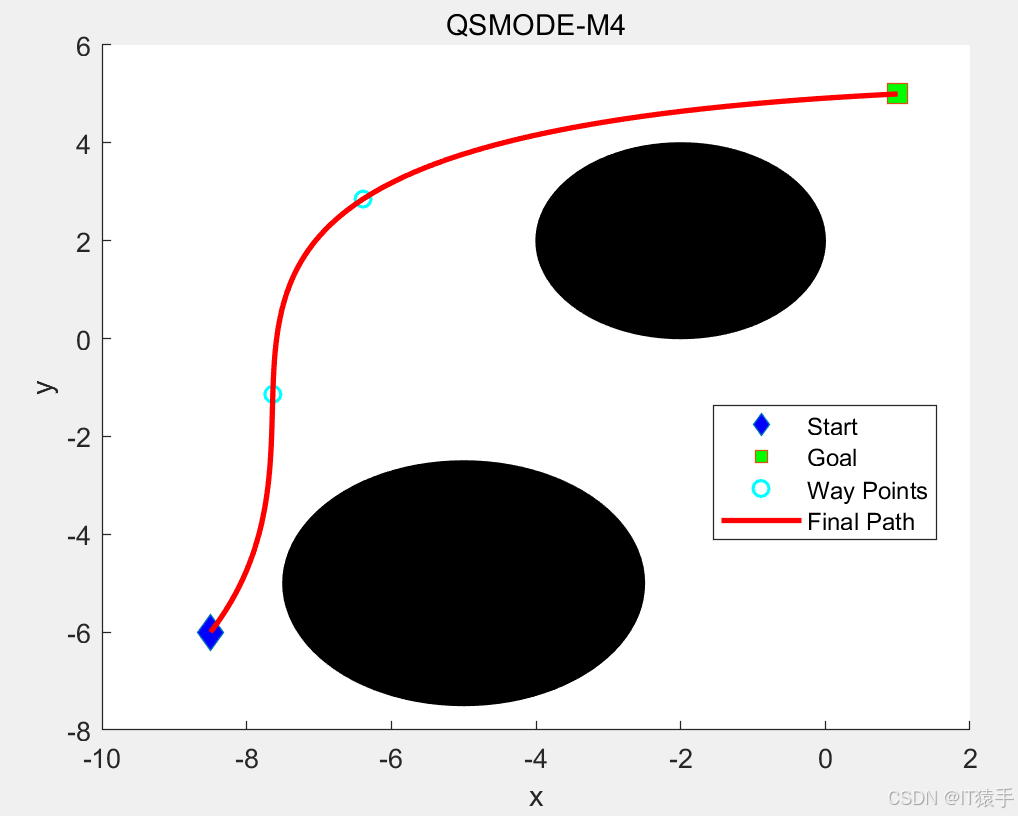
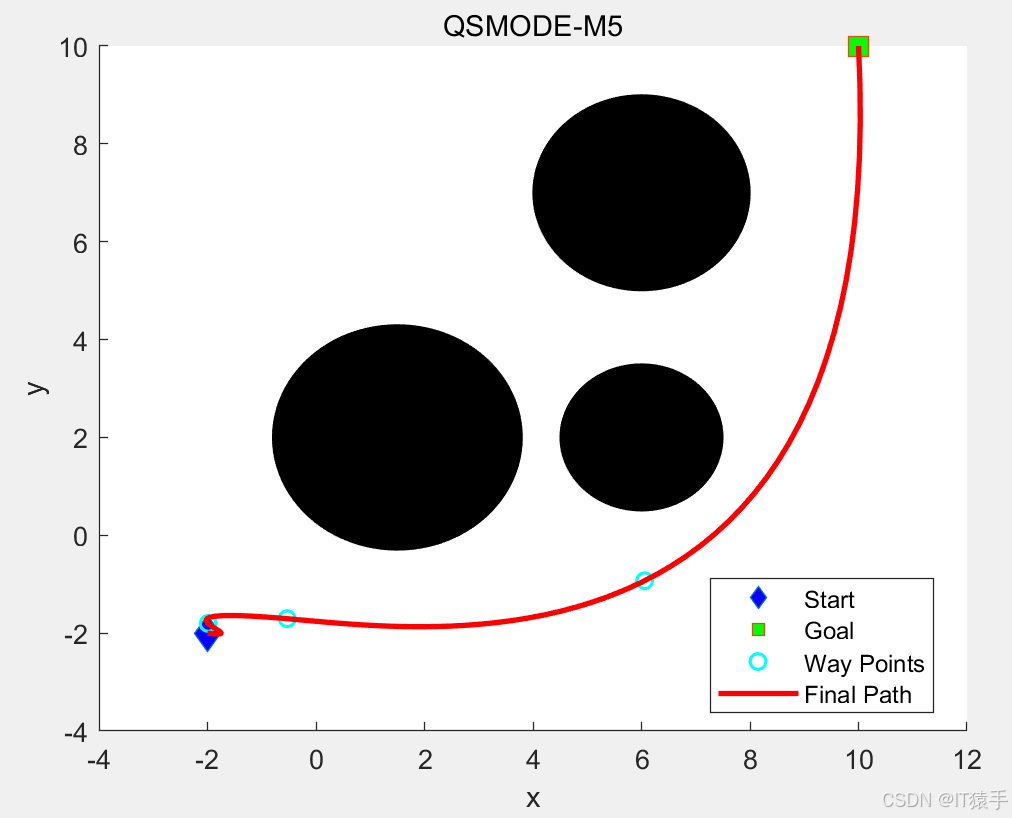
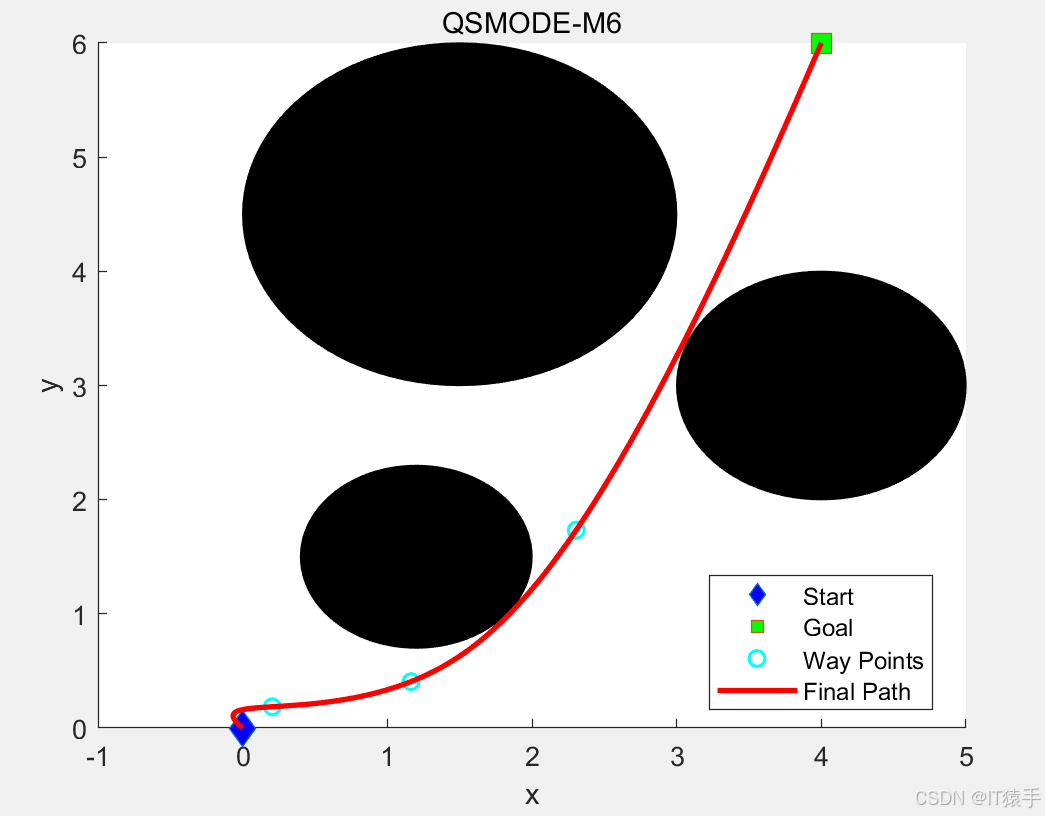
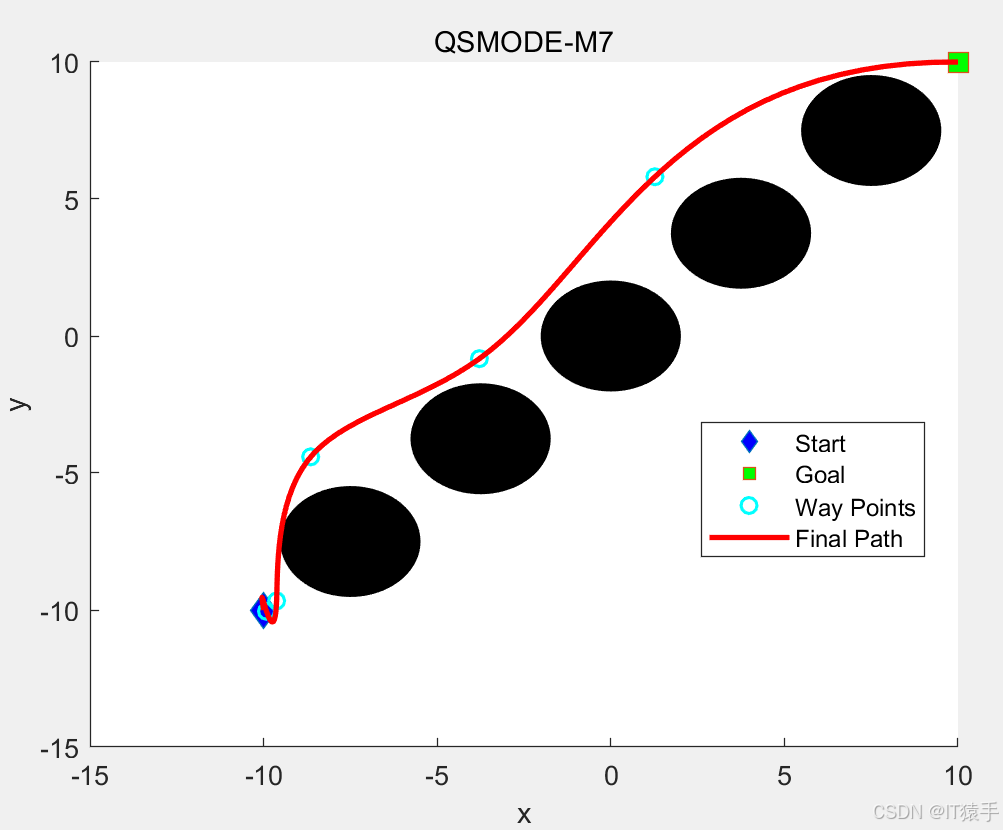
五、完整MATLAB代码见下方名片
参考文献:
1\]Reda, M., Onsy, A., Haikal, A.Y. et al. A novel reinforcement learning-based multi-operator differential evolution with cubic spline for the path planning problem. Artif Intell Rev 58, 142 (2025). https://doi.org/10.1007/s10462-025-11129-6 https://blog.csdn.net/weixin_46204734/article/details/146637089