【公式推导】AMP算法比BP算法强在哪（一）

文章目录

BP："树上聊天"的算法
[AMP：看起来像 BP，但实际上是"BP 的简化快版"](#AMP：看起来像 BP，但实际上是“BP 的简化快版”)
[AMP 的核心思想](#AMP 的核心思想)
- [要点1：AMP 很好地解决了稠密图中环路的回声](#要点1：AMP 很好地解决了稠密图中环路的回声)
- [要点2：AMP 把复杂的 BP 消息变成了"几个简单公式"](#要点2：AMP 把复杂的 BP 消息变成了“几个简单公式”)
- 要点3：从公式的角度上理解回声

BP："树上聊天"的算法

BP算法算的是一个精确的边缘概率，它做的是：因子图里面，每个节点（变量、因子）互相传消息。每个节点把邻居给的消息 相乘、求和，再发给其他邻居，最后推出来真正的边缘概率。

直觉上可以这样理解：BP = 每个节点都把"自己的意见 + 别人意见 "汇总，然后传下一个。

像一棵树里大家互相问意见，问着问着就知道答案了。

BP 是个 精确算法 ，特别是在"树形结构"时效果完美。(如果不知道BP算法原理的可以看我主页讲BP的那篇文章: 【一】和【二】）

AMP：看起来像 BP，但实际上是"BP 的简化快版"

AMP（Approximate Message Passing）出现的场景：常在压缩感知（Compressed Sensing）里用，比如你要从少量观测 y y y 里恢复高维向量 x x x，数学模型是：
y = A x + 噪声 y = A x + 噪声 y=Ax+噪声

这对应的因子图：

是非常稠密的
不是树！
有大量环
节点数目巨大（成千上万）

在这种图上直接跑 BP 会累死自己（计算量爆炸）。

AMP 的核心思想

AMP其实想这样做： "BP 太慢了，我能不能只保留 BP 的主要效果，把复杂的部分近似掉？"，这个是因为在稠密场景下，不同变量对因子的贡献其实是近似的，于是就得到 AMP ------一个跟 BP 非常像但超级简化的算法。

要点1：AMP 很好地解决了稠密图中环路的回声

你可以把它理解为：在复杂的因子图里（很多环），同一个节点的消息会绕一圈又回到自己身上，就像"回声"。

普通 BP 会把这个"回声"当成新的信息，所以会产生错误的推断，所以BP 聊天会被自己的回声骗到 。而AMP 会自动加一个"减掉回声"的项，会说："等等，这句可能是我自己上次说的话绕回来了，我把它减掉。"

我们通过以下方式来理解这个回声，首先从直观上可以看下面这个图，由于很稠密，因此存在很多环，我在图中只是写了其中的一个，实际上还有像 y 1 → x 1 → y 3 → x 2 y_1→x_1→y_3→x_2 y1→x1→y3→x2这样的很多类似的环路，这都会给BP的估计带来麻烦，因为引入了回声（之前的变量节点接收到自己的回声，会更确信这个信念是对的，因此就会往错误的方向进行更新）。

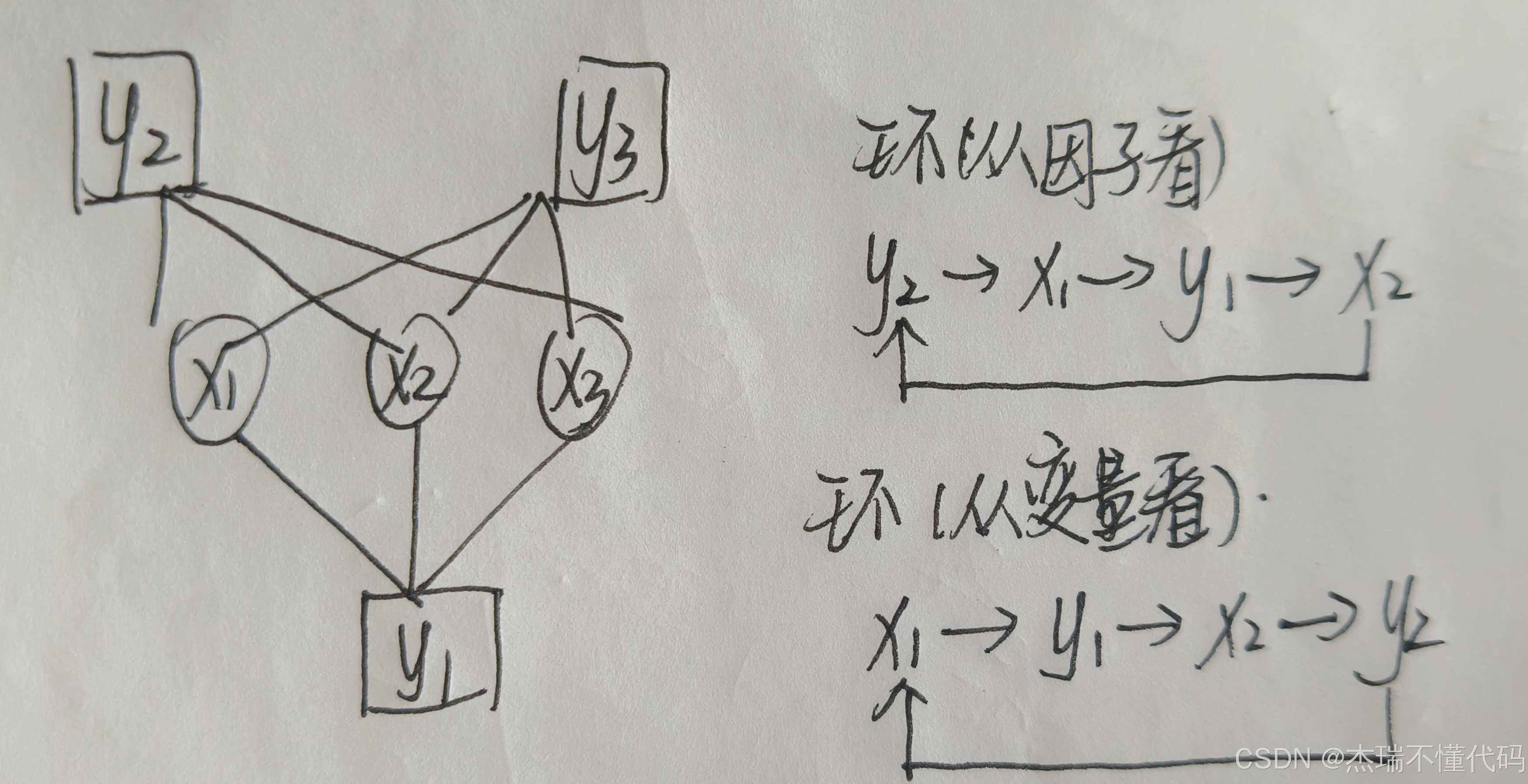
当然如果这里直接上公式，肯定大部分人就直接懵了，所以我还是先给大家普及一下AMP到底是怎么做的。

要点2：AMP 把复杂的 BP 消息变成了"几个简单公式"

在 BP 里，消息是函数，变量到因子： n ( x ) n(x) n(x)、因子到变量： m ( x ) m(x) m(x)，有点复杂。

在 AMP 里，所有消息被简化成：

一个残差 r r r
一个估计 x x x
一个简单的标量修正项

这比 BP 的"乘消息、求和、再发回去"要简单太多了。BP 要传好多复杂意见，AMP 只传简单几句话，而且还会自动消除回声。

AMP 不求精确，只求"平均意义下的好解"，BP 适用于树结构，会给出准确的边缘概率。AMP 适用于高维随机矩阵 A，会给出非常准确但不严格精确的结果 ------但这种"高维平均意义上的准确"在压缩感知里已经很好用了。

以一个线性高斯模型为例，我们先看BP是怎么做的：

y = A x + w , w ∼ N ( 0 , σ 2 I ) y = Ax + w,\quad w \sim \mathcal N(0,\sigma^2 I) y=Ax+w,w∼N(0,σ2I)

假设先验是可分解的 ：
p ( x ) = ∏ j = 1 N p X ( x j ) p(x) = \prod_{j=1}^N p_X(x_j) p(x)=j=1∏NpX(xj)

那么联合分布可以写成因子分解形式：

p ( x , y ) ∝ ∏ j p X ( x j ) ⏟ 先验因子 ⋅ ∏ p ( y i ∣ x ) ⏟ 观测因子 p(x,y) \propto \underbrace{\prod_{j} p_X(x_j)}{\text{先验因子}}\cdot \underbrace{\prod p(y_i \mid x)}{\text{观测因子}} p(x,y)∝先验因子 j∏pX(xj)⋅观测因子 ∏p(yi∣x)

这里是由基础的贝叶斯定理 p ( x , y ) = p ( x ) p ( y ∣ x ) p(x, y) = p(x) p(y | x) p(x,y)=p(x)p(y∣x)，其中假设各 x j x_j xj 可分，则 p ( x ) = ∏ j = 1 N p X ( x j ) p(x) = \prod_{j = 1}^{N} p_X(x_j) p(x)=∏j=1NpX(xj)，同时如果每个观测 y i y_i yi 受到独立噪声影响，则 p ( y ∣ x ) = ∏ i = 1 M p ( y i ∣ x ) p(y|x) = \prod_{i = 1}^{M} p(y_i|x) p(y∣x)=∏i=1Mp(yi∣x)，因此可以得到 p ( x , y ) = p ( x ) p ( y ∣ x ) = ( ∏ j p X ( x j ) ) ( ∏ i p ( y i ∣ x ) ) p(x, y) = p(x) p(y|x) = \left( \prod_{j} p_X(x_j) \right) \left( \prod_{i} p(y_i|x) \right) p(x,y)=p(x)p(y∣x)=(∏jpX(xj))(∏ip(yi∣x))

对每个观测 y i y_i yi，在这个线性高斯模型下有：

p ( y i ∣ x ) ∝ exp ⁡ ( − 1 2 σ 2 ( y i − ∑ k A i k x k ) 2 ) p(y_i \mid x) \propto \exp\left( -\frac{1}{2\sigma^2}\big(y_i - \sum_k A_{ik} x_k \big)^2 \right) p(yi∣x)∝exp(−2σ21(yi−k∑Aikxk)2)

这是因为，如果我们按维度展开： y i = ∑ j A i j x j + w i , w i ∼ N ( 0 , σ 2 ) y_i = \sum_{j} A_{ij} x_j + w_i, \quad w_i \sim \mathcal{N}(0, \sigma^2) yi=∑jAijxj+wi,wi∼N(0,σ2)，因为噪声是高斯的，所以我们给定 x ， y i x，y_i x，yi 的条件概率是： p ( y i ∣ x ) = N ( y i ; ∑ j A i j x j , σ 2 ) p(y_i|x) = \mathcal{N} \left( y_i; \sum_{j} A_{ij} x_j, \sigma^2 \right) p(yi∣x)=N(yi;∑jAijxj,σ2)，因此写成概率密度函数的形式： p ( y i ∣ x ) = 1 2 π σ 2 exp ⁡ ( − 1 2 σ 2 ( y i − ∑ j A i j x j ) 2 ) p(y_i|x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{1}{2\sigma^2} \left( y_i - \sum_{j} A_{ij} x_j \right)^2 \right) p(yi∣x)=2πσ2 1exp(−2σ21(yi−∑jAijxj)2)

于是对应的因子节点（记作 f i f_i fi）就是：

f i ( x ) : = p ( y i ∣ x ) ∝ exp ⁡ ( − 1 2 σ 2 ( y i − ∑ k A i k x k ) 2 ) f_i(x) := p(y_i\mid x) \propto \exp\left( -\frac{1}{2\sigma^2}\big(y_i - \sum_k A_{ik} x_k \big)^2 \right) fi(x):=p(yi∣x)∝exp(−2σ21(yi−k∑Aikxk)2)

在因子图上，BP 有两种消息：

变量节点 x j x_j xj→ 因子节点 f i f_i fi： n j → i ( x j ) n_{j\to i}(x_j) nj→i(xj)
因子节点 f i f_i fi → 变量节点 x j x_j xj： m i → j ( x j ) m_{i\to j}(x_j) mi→j(xj)

通用 sum-product 规则： 因子 → 变量：

m i → j ( x j ) ∝ ∫ f i ( x ) ∏ k ≠ j n k → i ( x k ) , d x k ≠ j m_{i\to j}(x_j) \propto \int f_i(x) \prod_{k\neq j} n_{k\to i}(x_k), d x_{k\neq j} mi→j(xj)∝∫fi(x)k=j∏nk→i(xk),dxk=j

也就是：固定 x j x_j xj，把因子上连着的其他变量 x k ( k ≠ j ) x_k(k\neq j) xk(k=j) 都积分掉。现在把刚刚的 f i ( x ) f_i(x) fi(x) 代入上面公式：

f i ( x ) ∝ exp ⁡ ( − 1 2 σ 2 ( y i − ∑ k A i k x k ) 2 ) f_i(x) \propto \exp\left( -\frac{1}{2\sigma^2} \left( y_i - \sum_k A_{ik} x_k \right)^2 \right) fi(x)∝exp −2σ21(yi−k∑Aikxk)2

代入因子消息公式：

m i → j ( x j ) ∝ ∫ exp ⁡ ( − 1 2 σ 2 ( y i − ∑ k A i k x k ) 2 ) ∏ k ≠ j n k → i ( x k ) d x k ≠ j = ∫ exp ⁡ ( − 1 2 σ 2 ( y i − ∑ k ≠ j A i k x k − A i j x j ) 2 ) ∏ k ≠ j n k → i ( x k ) d x k \begin{aligned} m_{i\to j}(x_j) &\propto \int \exp\left( -\frac{1}{2\sigma^2} \left( y_i - \sum_k A_{ik} x_k \right)^2 \right) \prod_{k\neq j} n_{k\to i}(x_k)d x_{k\neq j}\\ &= \int \exp\left( -\frac{1}{2\sigma^2} \left( y_i - \sum_{k\neq j} A_{ik} x_k - A_{ij} x_j \right)^2 \right) \prod_{k\neq j} n_{k\to i}(x_k)d x_{k} \end{aligned} mi→j(xj)∝∫exp −2σ21(yi−k∑Aikxk)2 k=j∏nk→i(xk)dxk=j=∫exp −2σ21 yi−k=j∑Aikxk−Aijxj 2 k=j∏nk→i(xk)dxk

因此在BP中，因子节点向变量节点的消息包含：

m i → j ( x j ) ∝ ∫ exp ⁡ ( − 1 2 σ 2 ( y i − ∑ k ≠ j A i k x k − A i j x j ) 2 ) ∏ k ≠ j n k → i ( x k ) d x k （标记式 1 ） m_{i\to j}(x_j) \propto \int \exp\left( -\frac{1}{2\sigma^2} \left( y_i - \sum_{k\neq j} A_{ik} x_k - A_{ij} x_j \right)^2 \right) \prod_{k\neq j} n_{k\to i}(x_k)d x_k （标记式1） mi→j(xj)∝∫exp −2σ21 yi−k=j∑Aikxk−Aijxj 2 k=j∏nk→i(xk)dxk（标记式1）

这个积分对所有变量节点求和，非常复杂。但是 AMP 完全不做这种求和 ，因为在压缩感知里面，因子数量成千上万，这种求和根本算不动。AMP^[1](#1) (Bayati & Montanari 2011) 使用的是：

高维极限（N→∞）下，因子 → 变量的消息可以被高斯化
所以整个"边缘概率"可以被一个简单的去噪函数(denoiser) 代替：

x t + 1 = η ( A T r t + x t ) x^{t+1} = \eta( A^T r^t + x^t ) xt+1=η(ATrt+xt)

其中 t t t 可以看成迭代次数， η η η 就是近似"边缘概率"的函数，也就是说等迭代结束的时候，我就可以用最后一步的 x x x 来近似这个边缘概率。AMP 把从变量流向因子的消息"折叠"为向量 x x x，BP 的：每条边一个函数消息 n k → i ( x k ) n_{k\to i}(x_k) nk→i(xk)，就变成AMP口中的："所有边的消息都长得差不多，我干脆用一个全局向量 x x x 来代表所有 n n n 消息 "，结果就是 n k → i ( x n ) ⟹ x k t n_{k \to i}(x_n) \Longrightarrow x_k^t nk→i(xn)⟹xkt。

那我们再回到标记式1，在这个式子中，传递的是因子→变量，这是 BP 最难算的一步：乘所有邻居消息 → 对所有变量求和"但是AMP 假设：

测量矩阵 A 随机且稠密
根据中心极限定理 此过程可以近似为高斯分布

于是：

r t = y − A x t + 1 δ r t − 1 ⟨ η ′ ( v t − 1 ) ⟩ r^t = y - A x^t + \frac{1}{\delta} r^{t-1} \langle \eta'(v^{t-1}) \rangle rt=y−Axt+δ1rt−1⟨η′(vt−1)⟩

这里的最后一项 Onsager correction 就是 BP 中因为有很多环而产生的"回声项"的修正。其中各个变量的含义如下：

符号	含义
x t x^t xt	第 t t t 轮的信号估计
r t r^t rt	第 t t t 轮的残差
v t − 1 = x t − 1 + A T r t − 1 v^{t-1}=x^{t-1} + A^T r^{t-1} vt−1=xt−1+ATrt−1	上一轮变量节点收到所有因子消息后的综合意见
A T r t A^T r^t ATrt	因子节点向变量节点的消息汇总
η ( ⋅ ) \eta(\cdot) η(⋅)	先验对应的去噪器（后验均值）
η ′ ( v t − 1 ) \eta'(v^{t-1}) η′(vt−1)	去噪器对输入的敏感度（局部放大因子）
⟨ η ′ ( v t − 1 ) ⟩ \langle\eta'(v^{t-1})\rangle ⟨η′(vt−1)⟩	所有节点敏感度的平均
δ = M / N δ = M/N δ=M/N	测量比（M代表测量数，N代表未知维数）

接下来我们把这些符号组合起来看，理解一下整个残差公式，把它拆成三部分：

r t = y − A x t + 1 δ r t − 1 ⟨ η ′ ( v t − 1 ) ⟩ r^t = y - A x^t + \frac{1}{\delta} r^{t-1} \langle \eta'(v^{t-1}) \rangle rt=y−Axt+δ1rt−1⟨η′(vt−1)⟩

第一部分：普通的残差 ： y − A x t y - A x^t y−Axt，简单理解为："当前估计 x t x^t xt 解释不了的部分。"

第二部分：Onsager correction ： 1 δ r t − 1 ⟨ η ′ ( v t − 1 ) ⟩ \frac{1}{\delta} r^{t-1}\langle \eta'(v^{t-1}) \rangle δ1rt−1⟨η′(vt−1)⟩，这是 BP 在稠密有环图上的修正项，由于AMP 的因子图非常稠密，BP 会产生"回声"， η ′ η' η′ 衡量估计会放大多少回声， r t − 1 r^{t-1} rt−1 是上一轮的回声源，乘上 η ′ η' η′ 的均值再缩放 δ δ δ 就得到"应当抵消的残差部分"。

由于 AMP 把所有消息折叠成两个向量 x x x 与 r r r：

x t + 1 = η ( A T r t + x t ) r t = y − A x t + Onsager correction x^{t+1}=\eta(A^Tr^t+x^t)\\ r^{t}=y-Ax^t+\text{Onsager correction} xt+1=η(ATrt+xt)rt=y−Axt+Onsager correction

这一步就把所有 BP 消息一次性计算完了。 因此来说，在BP中我们有叶子变量和叶子因子的说法，即

叶子变量→因子： n k → i ( x k ) = 1 n_{k\to i}(x_k) =1 nk→i(xk)=1
叶子因子→变量： m i → j ( x j ) = f i ( x j ) m_{i\to j}(x_j) = f_i(x_j) mi→j(xj)=fi(xj)

计算的时候从叶子往根传，来启动因子图的计算，但是AMP只有两个要更新的向量 x x x 与 r r r，一般初始化为：

初始 x x x 通常设为 0
初始残差 r 0 = y r⁰ = y r0=y

所以两者的主要不同可以表示为下表：

BP 做的事	AMP 如何改善
精确边缘化	用去噪函数替代，不做求和
变量→因子消息 = 乘函数	消息被折叠为向量 x x x
因子→变量消息 = 求和 × 乘积	变成残差 r r r 的线性算子 + 校正项
叶子节点规则	AMP 没有叶子概念
按图结构传递消息	AMP 全局一次性更新，无需传递
最终边缘 = 消息乘积	AMP 最终估计 = 去噪输出，不归一化

BP 的复杂度随图的连接数爆炸增长。AMP 的复杂度基本等于：做几次矩阵乘法（ A A A 和 A T Aᵀ AT），速度相当快。可以理解为：

BP：我适合小规模、树状问题。

AMP：我适合超大模型，几万维都能飞快跑。

要点3：从公式的角度上理解回声

在本文一开始，我只是给了一张简单的图，告诉回声是怎么来的，现在我们已经有了基本的AMP的处理思想，那我们用一个具体的矩阵来说明这个问题，还记得我们之前讲过 3×3 的因子图吗：

因子： f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3
变量： x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3

矩阵：
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} A= a11a21a31a12a22a32a13a23a33

例如变量 x 1 x_1 x1 的从因子来的消息是：

x 1 t + 1 = η ( x 1 t + ∑ i a i 1 r i t ) x_1^{t+1} = \eta\left(x_1^t + \sum_i a_{i1} r_i^t\right) x1t+1=η(x1t+i∑ai1rit)

而这个 r i t r_i^t rit 是什么？ ，按照 BP，它是从因子来的新消息，但实际上，注意看这行里面有 a i 1 x 1 t a_{i1} x_1^t ai1x1t：

r i t = y i − ∑ j a i j x j t r_i^t = y_i - \sum_j a_{ij} x_j^t rit=yi−j∑aijxjt

所以出现了如下循环： x 1 t x_1^t x1t 进入 r i t r_i^t rit，再通过 A T r t A^T r^t ATrt 回到 x 1 t + 1 x_1^{t+1} x1t+1，这个"自己影响自己"的路径不是一次，而是每轮都会发生：

x 1 t → r 1 t → x 1 t + 1 x_1^t \to r_1^t \to x_1^{t+1} x1t→r1t→x1t+1

它会导致：

BP 以为得到了大量新信息
实际上多数是「伪消息」（自己的回声）
所以更新会偏得特别厉害、或者震荡、甚至发散

而Onsager correction 解决的就是这件事。 另外需要澄清一点的是：AMP 简化了那么多步骤，是否和因子图没关系了？ 但是实际上AMP 仍然完全基于因子图（BP 简化），只是它把：

所有边的函数消息全部折叠进 → 两个全局向量（ x x x、 r r r）

当然本文只是简单地将BP算法和AMP算法进行了对比，一些细节例如高斯极限下是如何进行近似的，由于篇幅原因，并没有讲的很清楚，那么在下一期，尽量给大家把这个问题讲明白，我是不懂代码的杰瑞学长，我们下期再见！

Bayati M, Montanari A. The dynamics of message passing on dense graphs, with applications to compressed sensing[J]. IEEE Transactions on Information Theory, 2011, 57(2): 764-785. ↩︎