OPENCV(python）--初学之路（十二)霍夫线/圆变换

一前言

今天是周五，感觉时间过的好快，上周这个时候我还被病痛折磨，写人像识别，大家今天可以好好休息一下，但是今天我依旧奉上一篇重要的内容，大家周五快乐。

二主要内容--霍夫线/圆变换

一霍夫线变换

实际应用场景

• 文档扫描（检测文档边缘）

• 道路车道线检测

• 建筑图像中的直线检测

• 工业视觉中的边缘对齐检测

理论

如果您能够以数学形式表示该形状，则霍夫变换是一种用于检测任何形状的流行技术。它可以检测到形状，即使它被破坏或扭曲一点点。我们将看到它如何适用于生产线。

一条线可以表示为 y=mx+c 或以极坐标形式 表示为其中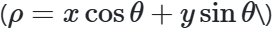是垂线从原点到直线的距离。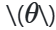是这条垂直线形成的角度，水平轴是逆时针测量的（该方向因你代表坐标系而变化。这种表示用于 OpenCV ）。检查下图

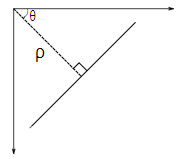
所以如果这条线经过原点以下，它会有一个小于 180 度的正角度。如果它在原点上方，我们不是取一个大于 180 的角，而是取一个小于 180 的负角度。任何垂直线都是 0 度，水平线是 90 度。

现在我们来看看霍夫变换是怎么作用于直线的。任何线都可以被表示成这两项。所以首先它创建了一个二维数组，或者是累加器(来保存这两个参数的值)然后他设置作为初始值。 令(二维数组的)行表示，令列表示 。数组的大小取决于你需要的精准度。假设说你想要角度的精度是精确到 1 度，那你就需要 180 列。而对于来说，最大可能的距离是图像的对角线长度。因此，要精确到一个像素的程度，行数应该是图像的对角长度。

想象有一张 100x100 的图像，它上面有一条水平的线条在图像正中间。取这条线的第一个点，你知道它的坐标 (x,y)值。现在，按照这条直线的等式，把值带入，并且查看你获取到的值。对每一对，我们都把它们在累加器中对应的值计数增加 1。而此时，在这个计数器中，单元 (50,90) 和其他单元一样计数等于 1。

现在去这条线上的第二个点，重复上面的步骤。增加单元中你拿到的对应的值(rho, theta)。这一次，单元(50,90)的计数增到到了 2。你实际上做的是投票投出值。你不断为这条直线上所有的点继续这个过程。在每一个点，单元(50,90)都会得票，而其他的单元有可能会得票，也有可能不会。按这个方案，最终单元 (50,90) 会获得最高的投票(译者注：在 100X100 的图像正中水平的直线到原点距离为 50，垂角 90 度)。所以最终搜索我们的累加器来找最高得票的单元，我们就会取到 (50,90)，这就说明图像中有一条线距离原点垂距 50，它过原点的垂线和水平线夹角为 90 度。这个过程很好的显示在了以下的动画中。（图片提供： Amos Storkey ）

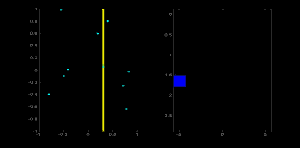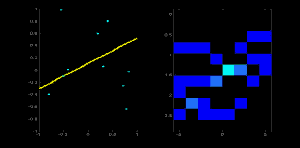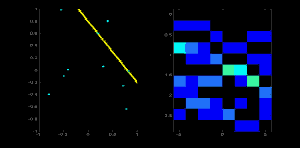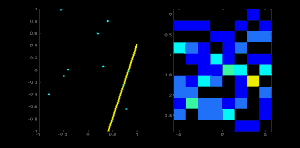
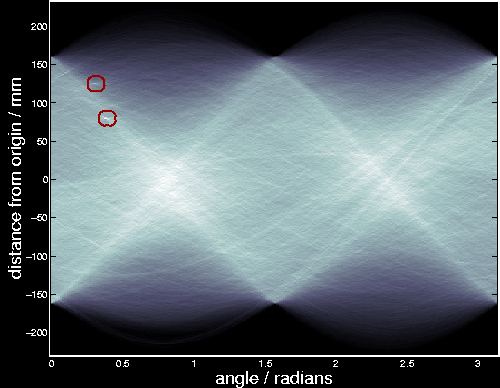
这就是霍夫变化针对直线工作的原理。非常简单，也许你可以用 Numpy 自己来实现它。以下是一张显示了累加器的图像。在某些地方的亮点说明它们是图像中可能线条的参数。（图片提供：维基百科）

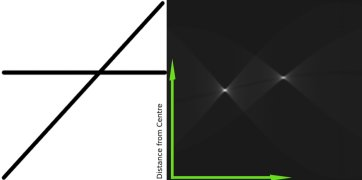
其实不用搞太明白，这是涉及原理的，我们暂时用不到，等用到的时候我会再次提到的。

OpenCV 中的霍夫变换

上面解释的这一堆东西，在 OpenCV 里都封装起来成为**cv.HoughLines（）** 函数了。

lines = cv.HoughLines(image, rho, theta, threshold[, lines[, srn[, stn[, min_theta[, max_theta]]]]])

必需参数：

• image: 输入图像（8位单通道二值图像）

• rho: ρ 的精度（以像素为单位）

• theta: θ 的精度（以弧度为单位）

• threshold: 累加器阈值（只有得票数超过此值的直线才会被检测出来）

可选参数：

• lines: 输出线向量（通常不用手动指定）

• srn, stn: 多尺度霍夫变换参数

• min_theta, max_theta: 检测的角度范围

返回值

返回一个 NumPy 数组，形状为 (n, 1, 2)，其中：

• n 是检测到的直线数量

• 每条直线由 (ρ, θ) 表示

  • ρ: 直线到原点的距离

  • θ: 直线的角度（弧度制）

它简单的返回了一个:math:(rho, theta)`值得数组。的单位是像素， 的单位是弧度。第一个参数，输入图像应该是个二元图像，所以在应用霍夫线性变换之前先来个阈值法或者坎尼边缘检测。第二、第三参数分别是 和 的精度。第四个参数则是一个阈值，它代表了一个单元被认为是一条直线需要获得的最低票数。要记住的是，得票数其实取决于这条直线穿过了多少个点。所以它也代表了应被检测出的线条最少有多长。

import cv2
import numpy as np

# 读取棋盘图像
image_path = 'path_to_your_chessboard_image.jpg'
img = cv2.imread(image_path)
original_img = img.copy()

# 转换为灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 边缘检测
edges = cv2.Canny(gray, 50, 150, apertureSize=3)

# 霍夫线变换检测直线
lines = cv2.HoughLines(edges, 1, np.pi/180, threshold=150)

# 绘制检测到的直线
if lines is not None:
    for line in lines:
        rho, theta = line[0]
        a = np.cos(theta)
        b = np.sin(theta)
        x0 = a * rho
        y0 = b * rho
        
        # 计算直线的两个端点
        length = 1000  # 足够长的线
        pt1 = (int(x0 + length*(-b)), int(y0 + length*(a)))
        pt2 = (int(x0 - length*(-b)), int(y0 - length*(a)))
        
        # 绘制直线
        cv2.line(img, pt1, pt2, (0, 0, 255), 2)

# 显示结果
cv2.imshow('Original', original_img)
cv2.imshow('Detected Lines', img)
cv2.waitKey(0)
cv2.destroyAllWindows()
 

如果大家不知道用什么图像可以找一张棋盘的照片。

效果如下

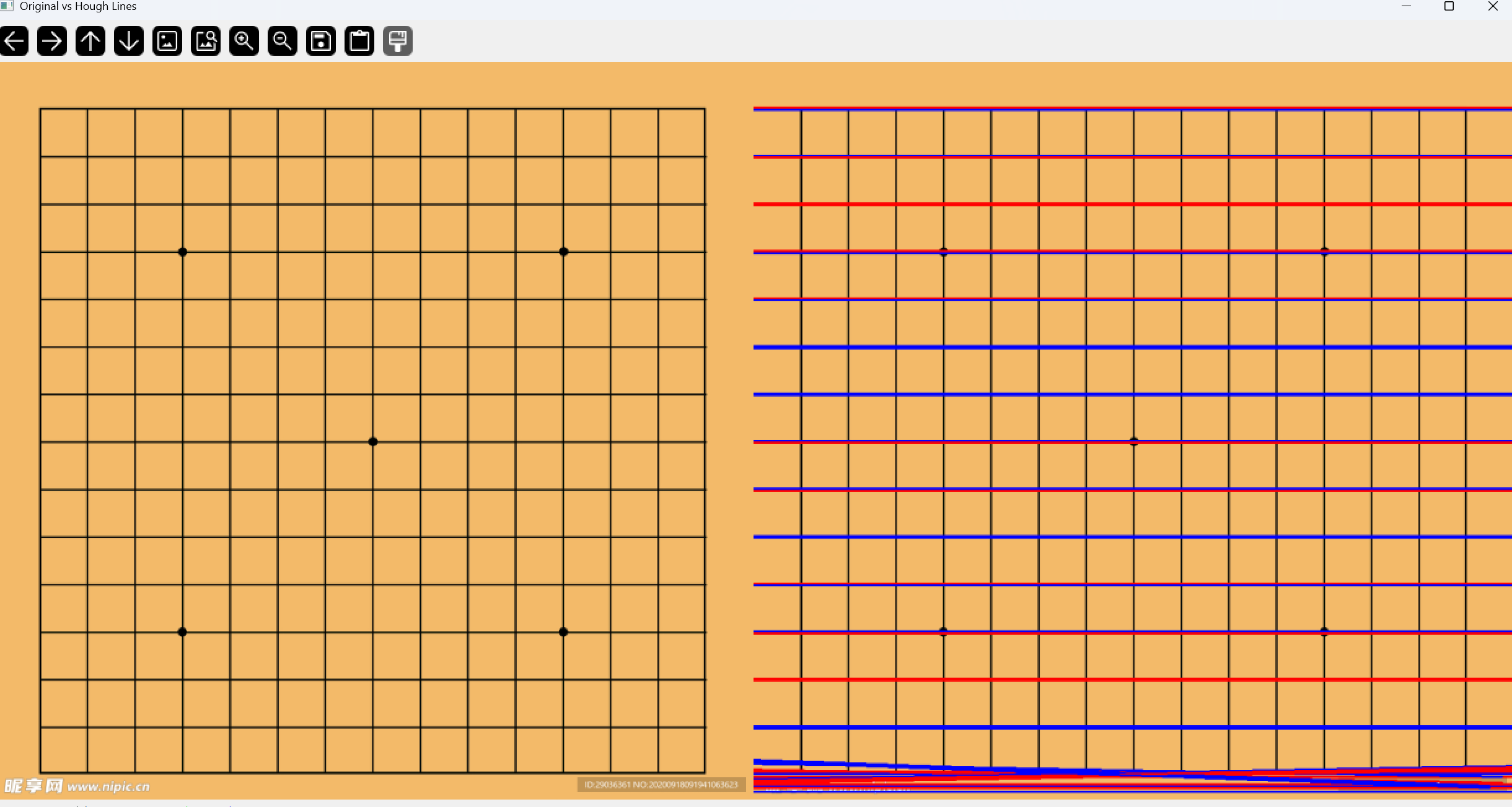
概率 Hough 变换

在霍夫变换中，你可以发现即使是一条仅有两个参数的直线，也需要用到大量的计算。概率霍夫变换是我们已知的，针对霍夫变换的优化方案。它不去取所有的点来列入考虑，取而代之的是取足够完成直线检测的这些点的随机子集。只要我们把阈值下调一点。下图在霍夫空间中比较了霍夫变换与概率霍夫变换（建议记住这个，用这个，效果更好）

OpenCV 实现基于使用 Matas，J。和 Galambos，C。和 Kittler，J.V。 [133] 的渐进概率 Hough 变换的线的鲁棒检测。使用的函数是 cv.HoughLinesP（） 。它比之前介绍的函数多出来两个参数：

lines = cv.HoughLinesP(image, rho, theta, threshold[, lines[, minLineLength[, maxLineGap]]])

• minLineLength - 最小线长。比这个值小的线条会被丢弃。
• maxLineGap - 允许线段之间的最大间隙，以便将(在同一条直线上的)线段视为同一条。

最好的是，它直接返回直线的两个端点。在前面的例子中，你只得到直线的参数，你必须找到所有的点。而这个方法，一切都是那么的直接和简单。

两种方法的比较

特性	cv.HoughLines()	cv.HoughLinesP()
返回值	(ρ, θ) 参数	线段端点 (x1,y1,x2,y2)
输出类型	无限长直线	有限长线段
速度	较慢	较快
内存使用	较高	较低
适用场景	需要直线参数时	大多数实际应用

代码如下：

import cv2 as cv
import numpy as np

# 读取图像
img = cv.imread(cv.samples.findFile(r'D:\python_code\pic\qipan.jpg'))
original = img.copy()
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# 边缘检测
edges = cv.Canny(gray, 50, 150, apertureSize=3)

# 概率霍夫线变换
lines = cv.HoughLinesP(edges, 1, np.pi/180, 100, 
                       minLineLength=50, maxLineGap=10)

# 绘制检测到的线段
if lines is not None:
    for line in lines:
        x1, y1, x2, y2 = line[0]
        cv.line(img, (x1, y1), (x2, y2), (0, 255, 0), 2)
        
    print(f"检测到 {len(lines)} 条线段")

# 并排显示原图和结果
result = np.hstack([original, img])

# 缩小显示
height, width = result.shape[:2]
scale = 0.5 # 缩小到50%
new_width = int(width * scale)
new_height = int(height * scale)
small_result = cv.resize(result, (new_width, new_height))

# 显示
cv.imshow('Original vs Result', small_result)
cv.waitKey(0)
cv.destroyAllWindows()
 

效果如下：

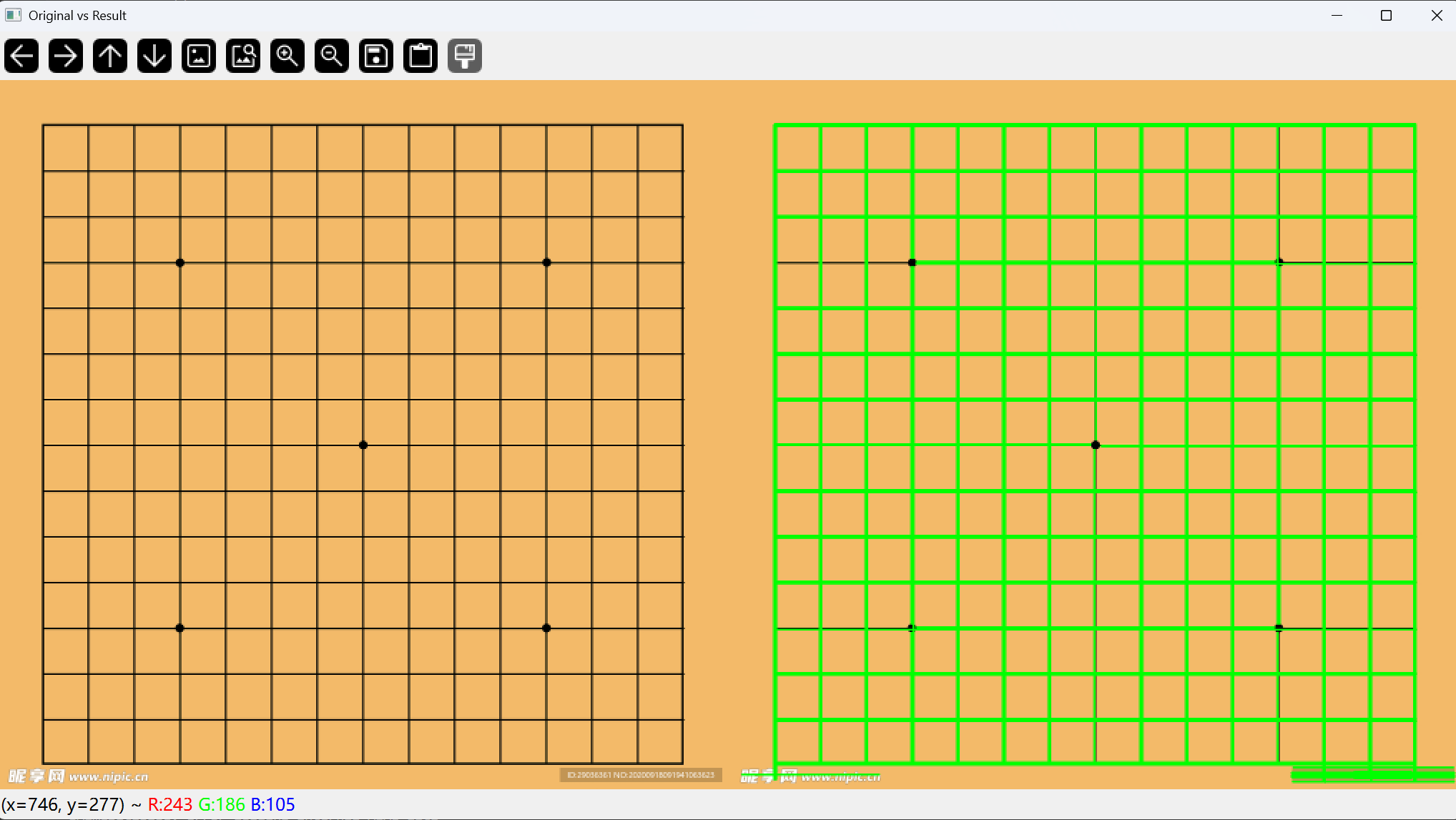
二霍夫圆变换

理论

圆圈在数学上表示为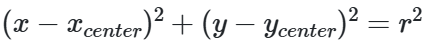其中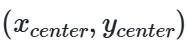是圆的中心， 是圆的半径。从这个公式来看，得知我们有三个参数，这样我们就需要一个三维度的累加器来做霍夫变换了，这样效率是非常低的。所以 OpenCV 用了更巧妙的方法Hough Gradient Method ，它利用了边缘的梯度信息。 我们在这里使用的函数是 cv.HoughCircles（） 。它的参数非常的多，这些参数在文档中都有详细的解释。所以我们直接上代码吧。

import numpy as np
import cv2 as cv

# 读取图像并转换为灰度图
img = cv.imread(r'D:\python_code\pic\opencv.jpg', 0)

# 应用中值滤波去除噪声
img = cv.medianBlur(img, 5)

# 将灰度图转换为彩色图以便绘制彩色圆形
cimg = cv.cvtColor(img, cv.COLOR_GRAY2BGR)

# 使用霍夫变换检测圆形
circles = cv.HoughCircles(img, cv.HOUGH_GRADIENT, 1, 20,
                          param1=50, param2=30, minRadius=0, maxRadius=0)

# 确保检测到圆形
if circles is not None:
    circles = np.uint16(np.around(circles))
    for i in circles[0, :]:
        # 绘制圆形
        cv.circle(cimg, (i[0], i[1]), i[2], (0, 255, 0), 2)
        # 绘制圆心
        cv.circle(cimg, (i[0], i[1]), 2, (0, 0, 255), 3)

# 显示结果
cv.imshow('detected circles', cimg)
cv.waitKey(0)
cv.destroyAllWindows()
 

效果如下

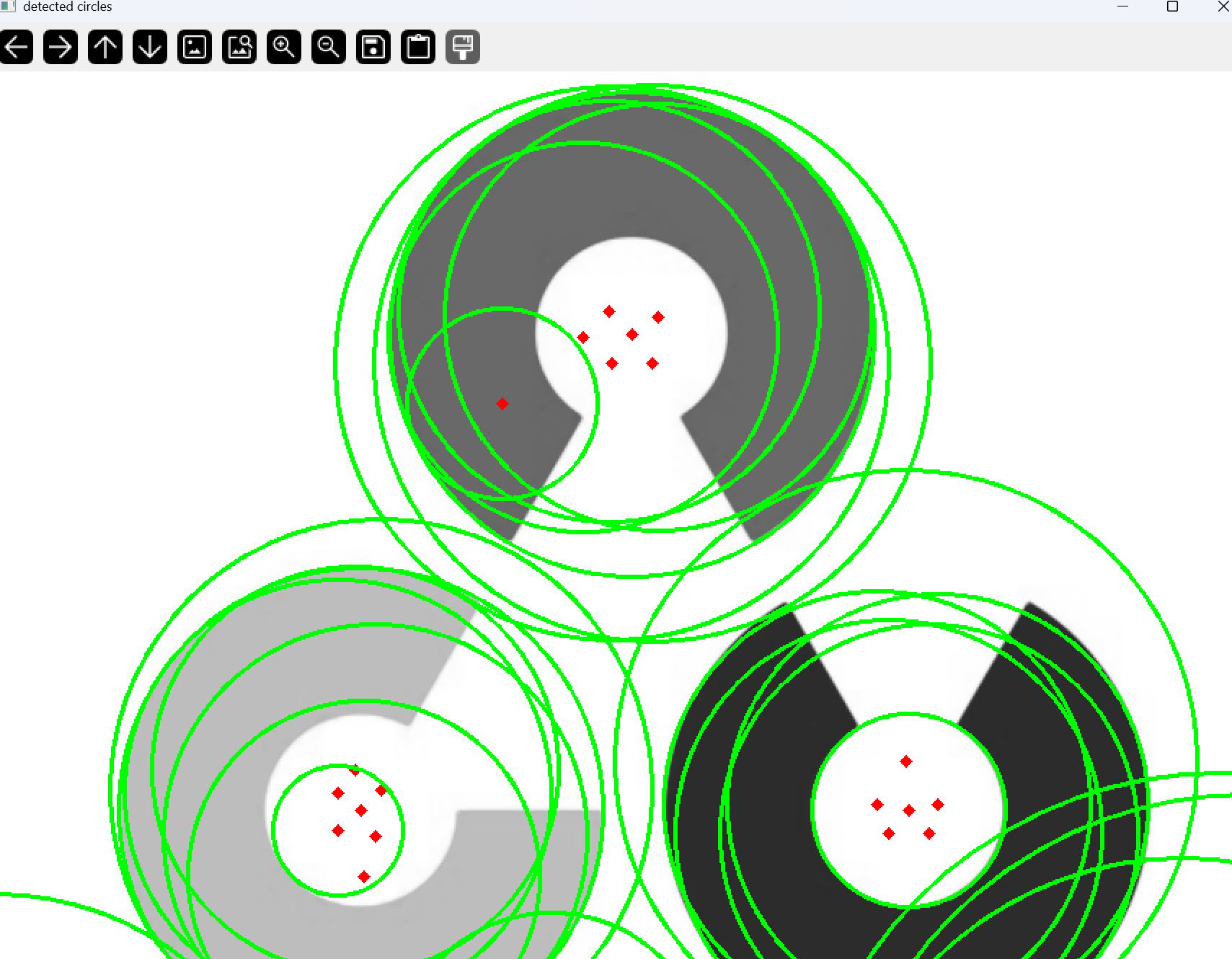
三最后一语

今天的内容还是比较有意思的，大家都可以试一试。

我关心我自己。越孤独，越无依无靠，越没有人来帮助我，我就越要自重。

------夏洛蒂·勃朗特《简·爱》

感谢观看，共勉！！