机器学习入门＜5＞支持向量机形象教学：寻找最安全的“三八线”，人人都能懂的算法核心

一、引言

想象一下，你被任命为一个村庄的新任村长 。村子里有两大家族：苹果家族 和橙子家族 。他们共同拥有一片土地，现在请你来主持公道，画一条分界线，把土地一分为二，一边种苹果，一边种橙子。

你拿到了一张地图，上面标着两家现有树木的位置（数据点）。作为一名力求公平且富有远见的村长，你会怎么画这条线？

是随便画一条线把点分开就完事，还是会深思熟虑，让这条线离两边的树都尽可能远一些？

选择后者，你就已经抓住了支持向量机最精髓的思想。今天，我们就用最生活化的语言和比喻，揭开SVM的神秘面纱。

二、核心目标：这堂课你就能明白的三件事

什么是"最大间隔"？ 为什么宽宽的"缓冲带"那么重要？
什么是"支持向量"？ 为什么说整个SVM模型只由少数几个"关键分子"决定？
SVM的核心思想是什么？ 它和逻辑回归等分类器根本的不同在哪里？

三、第一部分：生活中的"分界"难题------公平的起点

1. 故事场景：土地划分的智慧

我使用python语言画了一张苹果树和橙子树的分布地图。它先设置好中文显示，然后确定了两种树在坐标系里的具体位置：苹果树用红色三角形标记，橙子树用橙色圆形标记。接着创建了一个带网格的背景图，标注了坐标轴名称，加了标题和图例，最后把所有树按照坐标位置画出来，形成了一张清晰的果树分布图。

假设地图（特征空间）如下，三角形代表苹果树，圆形代表橙子树。

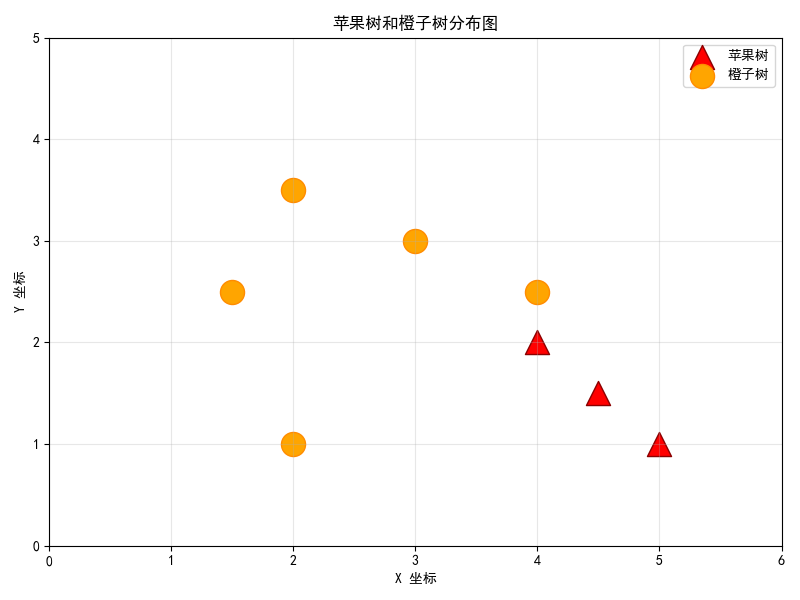
提问：如果让你画分界线（决策边界），上图中有无数种画法，哪一条最好？

我们希望这条线离两边的树都尽量远 。这样，即使未来树长大了（数据有小幅波动或噪声），或者新栽的树位置有点偏差（新样本），它们也不太容易不小心"越界"跑到对面家族的领地去。这个"缓冲地带"就是"间隔（Margin）"。

2. 对比实验：三条分界线的命运

我们来想象三种画法：

画法一（紧贴苹果） ：苹果家族抗议："我们的生存空间被压缩了！稍微长歪一点就过界了！" -> 间隔很小，对苹果侧容错率极低。
画法二（紧贴橙子） ：橙子家族抱怨："太不公平了！" -> 间隔很小，对橙子侧容错率极低。
画法三（居中且宽阔） ：两边都说："这样大家都安全，很公平！" -> 间隔最大化，对两侧的容错能力都很强。

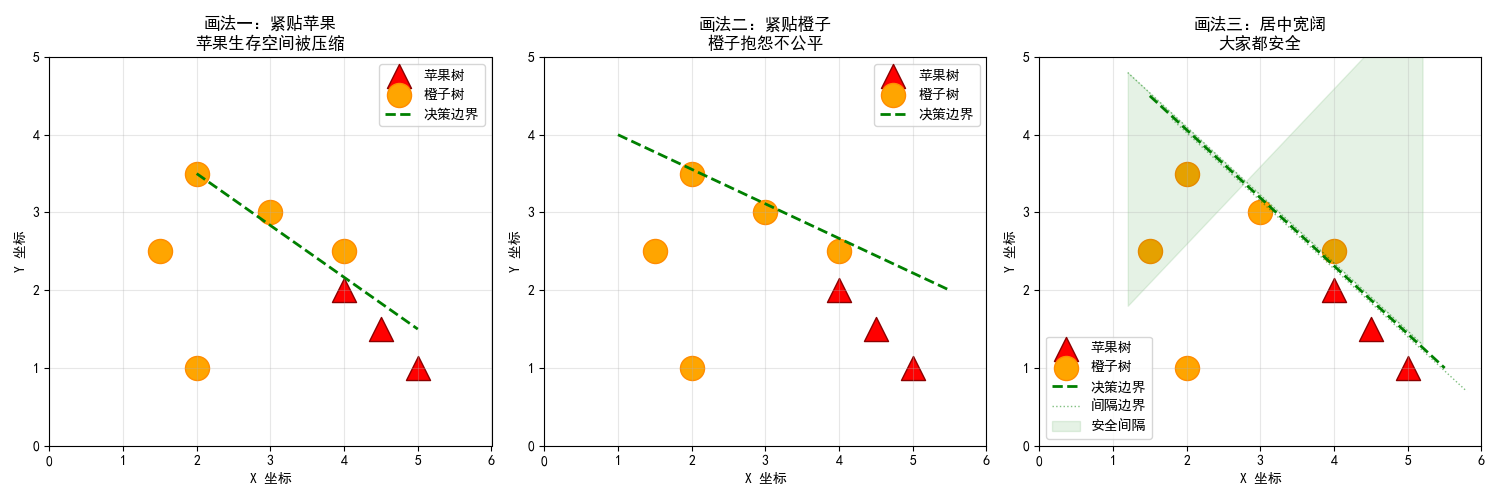
结论：中间的、离两边都最远的线，能创造最宽的"无人区"，是最安全、最稳健 的选择。这就是SVM追求的 "最大间隔（Maximum Margin）"。

四、第二部分：核心概念解剖------从一条线到两条街

1. 可视化演示：SVM画的不只是一条线

SVM的智慧在于，它不直接画最终的分界线，而是先规划出两条平行的"街道边界"：

一条街这边，必须全是苹果树。
另一条街那边，必须全是橙子树。
两条街中间的区域，就是"间隔"。

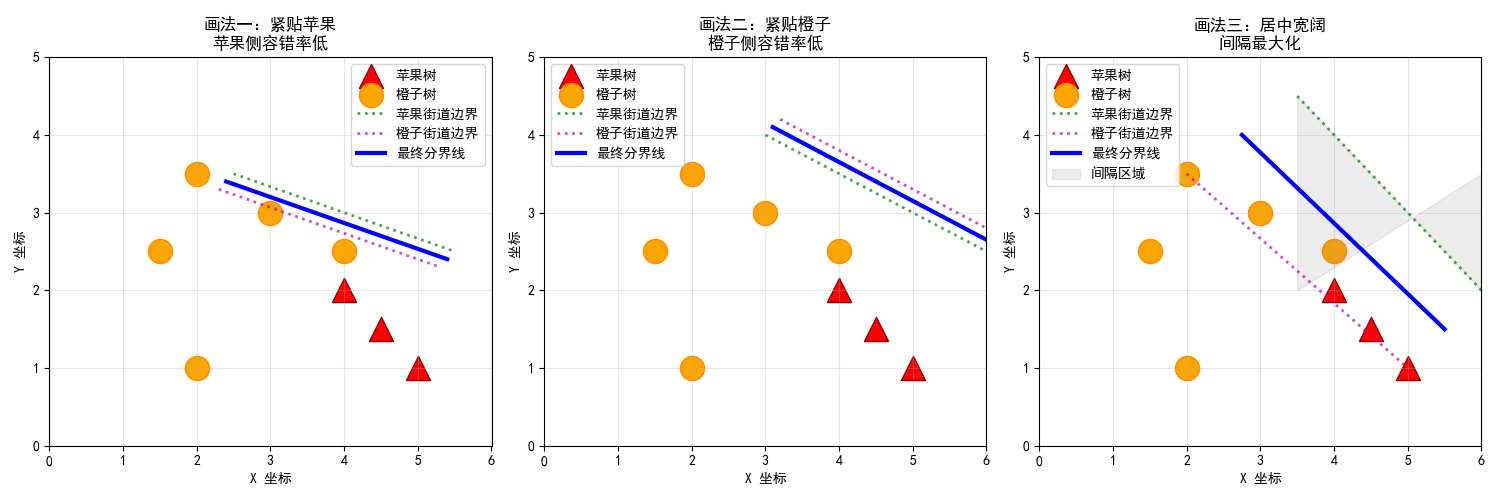
我们的目标变得非常直观：让这两条街之间的"马路"越宽越好！

通过动画或图形演示可以看到，随着我们调整中间线的方向和位置，这两条平行街的宽度会变化。SVM算法就是在自动寻找那个能让街道宽度达到最大的完美位置和方向。

2. "支持向量"------决定大局的少数关键点

当街道被拓到最宽时，你会发现一个神奇的现象：

总有那么几棵树，它们恰好站在了街道的边线上，不偏不倚。

这些站在边线上的标兵树 ，就是支持向量！

这是SVM最核心、也最反直觉的洞察之一：

整个村庄的划分，其实只由这几棵标兵树决定！ 其他树，只要不挤到街道里面来，你把它挪远一点、挪近一点，都不会改变分界线和街道的宽度。
但是，只要你移动任意一棵标兵树，整条分界线和街道的规划都要随之改变！

比喻：支持向量就像两个国家边界线上的哨兵。国界线这个决策边界划在哪里，不取决于腹地深处的居民，而完全取决于这些前沿哨兵所站的位置。SVM这个机器，就是由这些支持着间隔的向量所驱动的。

五、第三部分：为什么"最大间隔"如此重要？

1. 泛化能力测试：新树来了怎么办？

春天，村里新种了一批树（新数据/测试数据）。它们的位置可能和老的训练数据略有不同。

场景一（窄间隔）：缓冲带很窄，新树只要种得稍微偏一点，就可能被误判为属于对面家族。
场景二（宽间隔）：缓冲带很宽，新树即便有些位置偏差，也仍然稳稳地落在自己家族这一侧。

结论：最大间隔带来了最强的泛化能力。 它让模型对未知数据的预测更加可靠和健壮。

2. 现实世界类比

垃圾邮件过滤：如果"垃圾"和"正常"的界限宽，那些模棱两可的邮件就不容易错判。
医疗诊断：如果"健康"指标和"患病"指标间的界限宽，处于临界值的"疑似"病例就能被更安全地对待。
人脸识别：张三和李四的特征界限越宽，即使光照、角度变化，系统也能轻松区分。

核心公式（非数学） ：宽间隔 ≈ 强健性 ≈ 好的泛化能力

六、第四部分：非线性情况------"空中俯视"的魔法

1. 难题出现：混在一起的圈子

现实并不总是美好的线性可分。很多时候数据是这样：

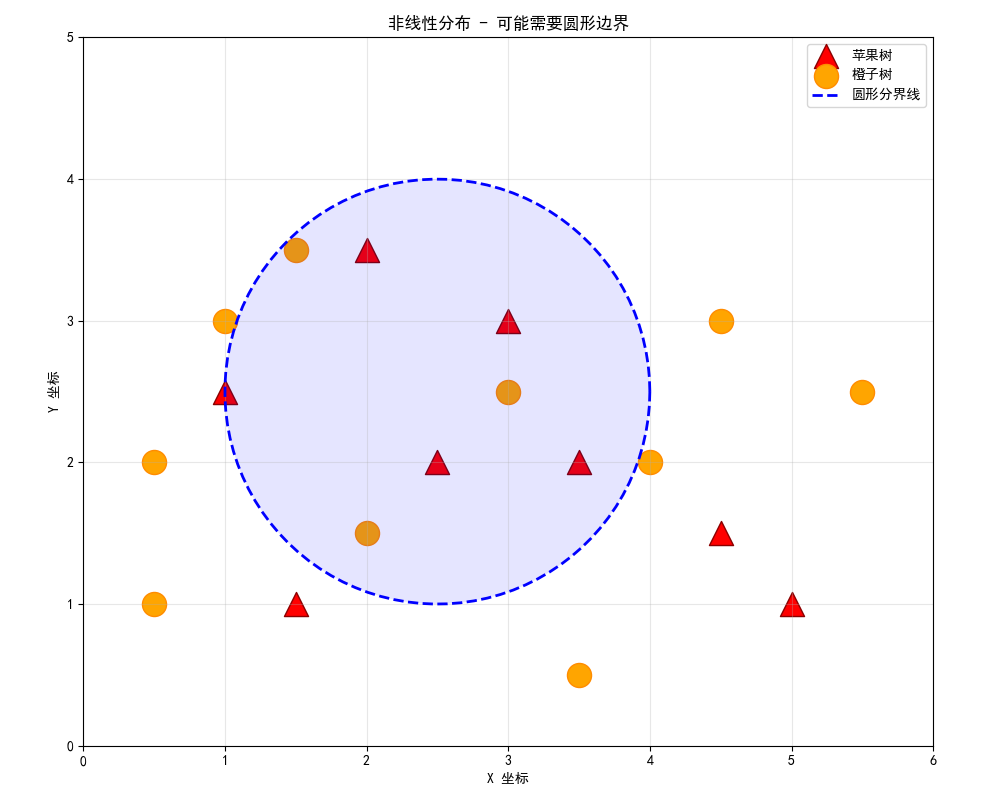
挑战：谁能用一条直线把它们完美分开？答案是不可能。

2. 升维思考：从地面飞到空中

SVM解决此问题的策略充满想象力：如果在地上（二维空间）分不开，我们飞到天上去（高维空间）看呢？

比喻：假设苹果树发出红光，橙子树发出黄光。在地面上看，光斑混在一起。但红光和黄光的强度或波长（第三个维度） 可能不同。从空中（三维）俯视，红光团和黄光团可能在不同的高度 ，这时我们很容易用一个平面（在高维空间，平面就是"线"）将它们切开。

这个"飞到空中"的梯子或飞行器，在SVM里就叫做核函数。 它是一组神奇的数学工具（如多项式核、高斯RBF核），能将数据从原始空间映射到更高维的特征空间，而无需真正计算高维坐标（核技巧）。

3. 回到地面：曲线诞生了

当我们在三维空间找到那个最大间隔的分割平面后，再把它投影回二维地面......

瞧！一条优雅的曲线 出现了。这条曲线虽然在二维空间是弯曲的，但它依然坚守着SVM的信仰：在映射后的高维空间里，它仍是具有最大间隔的线性分界。

现在我使用python实现2与3

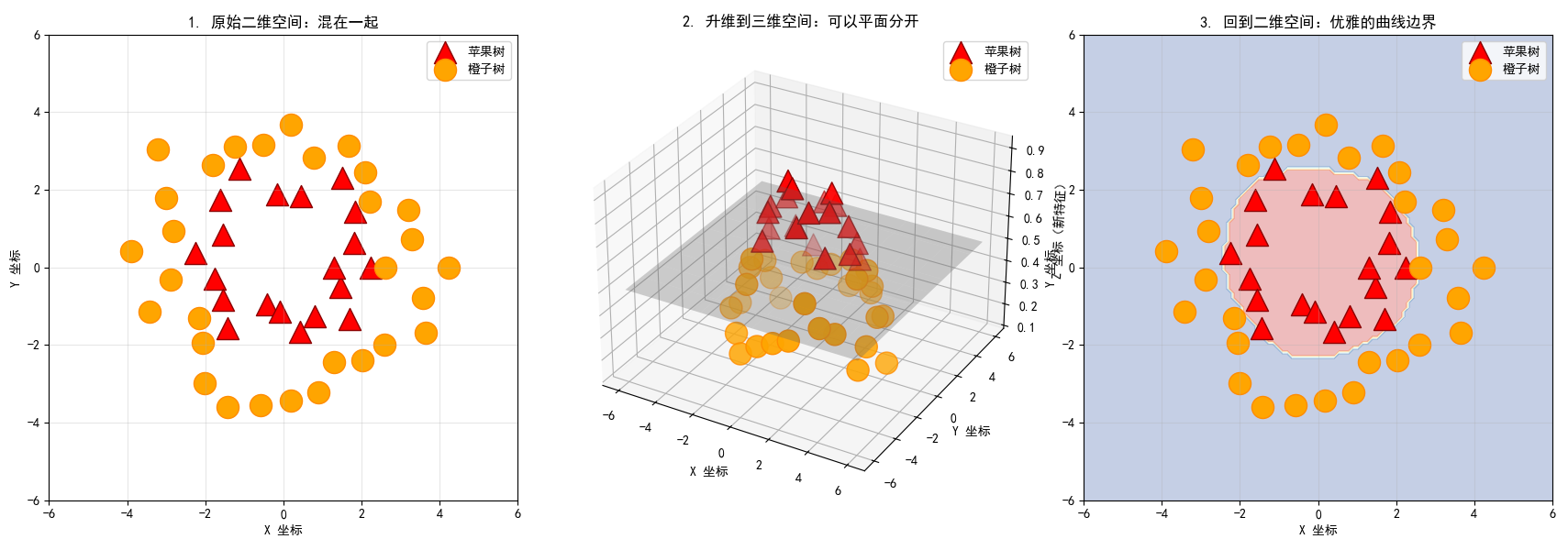
通过三个子图展示了SVM处理非线性问题的完整过程：

图1：原始二维空间
- 苹果树（红色三角形）和橙子树（橙色圆形）交错分布
- 无法用一条直线将它们分开
- 展示了地面视角的困境
图2：升维到三维空间
- 使用3D图形展示，我们"飞到了空中"
- 添加了第三个维度Z（通过高斯RBF核函数模拟）
- 在这个新空间中，两种树分布在不同的高度
- 灰色平面示意了在高维空间中可以用平面轻松分开它们
图3：回到二维空间的曲线边界
- 使用SVM（带RBF核）训练分类器
- 将高维空间的决策边界投影回二维空间
- 投影结果是一条优美的曲线，完美地分开了两种树
- 区域着色显示了分类器的置信度

解释：

核心概念展示：

核函数：图2中的Z轴变化模拟了核函数的效果，它将数据从二维空间映射到三维空间
最大间隔：图3中的曲线保持了SVM的最大间隔特性（在高维空间中）
非线性可分：展示了SVM如何处理原始空间中线性不可分的问题

这个可视化清楚地展示了SVM的核心思想：通过核函数将数据映射到高维空间，在高维空间中寻找最大间隔线性分类器，然后将其投影回原始空间，形成非线性决策边界。

七、总结升华：SVM的哲学与三板斧

1. 全过程比喻回顾

SVM就像一个睿智的边界谈判专家：

找标兵（支持向量）：先确定边界上最关键的代表点。

画街道（最大间隔）：为标兵们规划出尽可能宽的缓冲走廊。

定中线（决策边界）：在走廊正中央划下最终的分界线。

备魔镜（核函数）：遇到复杂地形时，使用"维度提升魔镜"转换视角，在更高维度轻松完成1-3步。

2. 核心思想三句话

不偏不倚：分界线必须公平，追求对两类样本的最大化最小距离。
宽以待人：留出最宽的缓冲空间，以增强模型的容错和泛化能力。
抓大放小：只关注边界上的关键样本（支持向量），无视远离边界的内部点，使得模型简洁而强大

3. 极简代码感知

如果对代码不感冒，可以跳过。但它能让你感受SVM的简洁。

python 复制代码

# 导入工具包
from sklearn import svm
import numpy as np

# 1. 准备数据：[甜度, 酸度] 作为特征
X = np.array([[1, 2], [2, 3], [3, 3], [6, 5], [7, 8], [8, 8]])  # 6个水果的特征
y = np.array([0, 0, 0, 1, 1, 1])  # 标签：0=苹果，1=橙子

# 2. 创建SVM分类器，使用线性核
clf = svm.SVC(kernel='linear')
clf.fit(X, y)  # 训练模型（自动寻找最大间隔）

# 3. 预测一个新水果
new_fruit = np.array([[4, 4.5]])  # 新水果特征
prediction = clf.predict(new_fruit)
print(f"预测结果: 这个水果是{'橙子' if prediction[0]==1 else '苹果'}")

# 4. 查看决定模型的关键------支持向量
print(f"\n支持向量（标兵树）的位置:\n{clf.support_vectors_}")
print(f"它们在原始数据中的索引: {clf.support_}")

# 尝试将 kernel='linear' 改为 kernel='rbf'，看看非线性边界的效果！

预测结果: 这个水果是苹果

支持向量（标兵树）的位置:
$\[3. 3.$ $6. 5.\]$
它们在原始数据中的索引: [2 3]

进程已结束，退出代码为 0

八、使用到的代码

1.苹果树与橙子树的地图

python 复制代码

import matplotlib.pyplot as plt
import numpy as np

# 设置中文字体（避免乱码）
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 树的位置数据
A = np.array([[4, 2], [4.5, 1.5], [5, 1]])  # 苹果树
O = np.array([[2, 3.5], [3, 3], [1.5, 2.5], [4, 2.5], [2, 1]])  # 橙子树

# 创建图形
plt.figure(figsize=(8, 6))

# 用不同的标记画树
plt.scatter(A[:, 0], A[:, 1], s=300, c='red', marker='^', label='苹果树', edgecolors='darkred')
plt.scatter(O[:, 0], O[:, 1], s=300, c='orange', marker='o', label='橙子树', edgecolors='darkorange')

# 设置图形属性
plt.xlabel('X 坐标')
plt.ylabel('Y 坐标')
plt.title('苹果树和橙子树分布图')
plt.grid(True, alpha=0.3)
plt.legend()
plt.axis([0, 6, 0, 5])
plt.tight_layout()
plt.show()

2.对比实验：三条分界线的绘制

python 复制代码

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

A = np.array([[4, 2], [4.5, 1.5], [5, 1]])
O = np.array([[2, 3.5], [3, 3], [1.5, 2.5], [4, 2.5], [2, 1]])

# 创建三个子图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

# 三条不同的边界线参数
boundaries = [
    (2, 3.5, 5, 1.5, "画法一：紧贴苹果\n苹果生存空间被压缩"),  # 边界线1
    (1, 4, 5.5, 2, "画法二：紧贴橙子\n橙子抱怨不公平"),  # 边界线2
    (1.5, 4.5, 5.5, 1, "画法三：居中宽阔\n大家都安全")  # 边界线3
]

for i, (x1, y1, x2, y2, title) in enumerate(boundaries):
    ax = axes[i]

    # 画树
    ax.scatter(A[:, 0], A[:, 1], s=300, c='red', marker='^', label='苹果树', edgecolors='darkred')
    ax.scatter(O[:, 0], O[:, 1], s=300, c='orange', marker='o', label='橙子树', edgecolors='darkorange')

    # 画决策边界
    ax.plot([x1, x2], [y1, y2], 'g--', linewidth=2, label='决策边界')

    # 对于第三个图，添加安全间隔区域
    if i == 2:
        # 计算间隔边界（与决策边界平行但偏移的线）
        # 上边界
        ax.plot([x1 - 0.3, x2 - 0.3], [y1 + 0.3, y2 + 0.3], 'g:', linewidth=1, alpha=0.5, label='间隔边界')
        # 下边界
        ax.plot([x1 + 0.3, x2 + 0.3], [y1 - 0.3, y2 - 0.3], 'g:', linewidth=1, alpha=0.5)
        # 填充间隔区域
        ax.fill_between([x1 - 0.3, x2 - 0.3], [y1 + 0.3, y2 + 0.3], [x1 + 0.3, x2 + 0.3],
                        alpha=0.1, color='green', label='安全间隔')

    # 图形设置
    ax.set_xlabel('X 坐标')
    ax.set_ylabel('Y 坐标')
    ax.set_title(title)
    ax.grid(True, alpha=0.3)
    ax.legend()
    ax.axis([0, 6, 0, 5])

plt.tight_layout()
plt.show()

3.SVM分割橘子树和苹果数的分布

python 复制代码

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

A = np.array([[4, 2], [4.5, 1.5], [5, 1]])
O = np.array([[2, 3.5], [3, 3], [1.5, 2.5], [4, 2.5], [2, 1]])

# 创建三个子图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

# 三个不同的边界线配置
street_configs = [
    # 紧贴苹果：街道边界靠苹果，间隔小
    {
        'apple_street': (2.5, 3.5, 5.5, 2.5),  # 苹果街道边界
        'orange_street': (2.3, 3.3, 5.3, 2.3),  # 橙子街道边界
        'decision_boundary': (2.4, 3.4, 5.4, 2.4),  # 决策边界
        'title': '画法一：紧贴苹果\n苹果侧容错率低'
    },
    # 紧贴橙子：街道边界靠橙子，间隔小
    {
        'apple_street': (3, 4, 6, 2.5),
        'orange_street': (3.2, 4.2, 6.2, 2.7),
        'decision_boundary': (3.1, 4.1, 6.1, 2.6),
        'title': '画法二：紧贴橙子\n橙子侧容错率低'
    },
    # 居中宽阔：街道边界距离大，间隔宽
    {
        'apple_street': (3.5, 4.5, 6, 2),
        'orange_street': (2, 3.5, 5, 1),
        'decision_boundary': (2.75, 4, 5.5, 1.5),
        'title': '画法三：居中宽阔\n间隔最大化'
    }
]

for i, config in enumerate(street_configs):
    ax = axes[i]

    # 画树
    ax.scatter(A[:, 0], A[:, 1], s=300, c='red', marker='^', label='苹果树', edgecolors='darkred')
    ax.scatter(O[:, 0], O[:, 1], s=300, c='orange', marker='o', label='橙子树', edgecolors='darkorange')

    # 画两条平行的"街道边界"
    x1_app, y1_app, x2_app, y2_app = config['apple_street']
    x1_ora, y1_ora, x2_ora, y2_ora = config['orange_street']

    # 苹果侧的街道边界（必须全是苹果树的一侧）
    ax.plot([x1_app, x2_app], [y1_app, y2_app], 'g:', linewidth=2, alpha=0.7, label='苹果街道边界')

    # 橙子侧的街道边界（必须全是橙子树的一侧）
    ax.plot([x1_ora, x2_ora], [y1_ora, y2_ora], 'm:', linewidth=2, alpha=0.7, label='橙子街道边界')

    # 画最终的分界线（决策边界） - 两条街道边界的中间线
    x1_dec, y1_dec, x2_dec, y2_dec = config['decision_boundary']
    ax.plot([x1_dec, x2_dec], [y1_dec, y2_dec], 'b-', linewidth=3, label='最终分界线')

    # 对于第三个图，填充"间隔"区域
    if i == 2:
        # 创建间隔区域的多边形
        ax.fill_between([x1_app, x2_app], [y1_app, y2_app], [x1_ora, y1_ora],
                        alpha=0.15, color='gray', label='间隔区域')

    # 图形设置
    ax.set_xlabel('X 坐标')
    ax.set_ylabel('Y 坐标')
    ax.set_title(config['title'])
    ax.grid(True, alpha=0.3)
    ax.legend()
    ax.axis([0, 6, 0, 5])

plt.tight_layout()
plt.show()

4.橘子树和苹果数的非线性分布

python 复制代码

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 非线性分布数据 - 交错分布
# 图2: 非线性分布示意图
#    ^
#    |   O  A  A  O
#    |  A  O   O  A
#    |   O  A  A  O
#    |------------>

# 创建交错分布的苹果树和橙子树
np.random.seed(42)  # 设置随机种子以确保可重复性

# 苹果树 (A) 的位置 - 非线性分布
A = np.array([
    [2.0, 3.5],  # 右上区域
    [3.0, 3.0],
    [3.5, 2.0],
    [4.5, 1.5],  # 右下区域
    [5.0, 1.0],
    [2.5, 2.0],  # 中间偏右
    [1.0, 2.5],  # 左边也有苹果树
    [1.5, 1.0]
])

# 橙子树 (O) 的位置 - 环绕分布
O = np.array([
    [1.0, 3.0],  # 左上区域
    [0.5, 2.0],
    [1.5, 3.5],
    [2.0, 1.5],  # 中间区域
    [3.0, 2.5],
    [4.0, 2.0],  # 右上区域
    [4.5, 3.0],
    [5.5, 2.5],  # 右边区域
    [0.5, 1.0],  # 左下区域
    [3.5, 0.5]
])

plt.figure(figsize=(10, 8))

# 画树
plt.scatter(A[:, 0], A[:, 1], s=300, c='red', marker='^', label='苹果树', edgecolors='darkred')
plt.scatter(O[:, 0], O[:, 1], s=300, c='orange', marker='o', label='橙子树', edgecolors='darkorange')

# 添加一条可能的分界线（非线性）
# 这条分界线展示了需要非线性边界来分离两种树
x_boundary = np.linspace(0, 6, 100)
y_boundary = 2.5 - 0.2*(x_boundary-3)**2  # 抛物线形状的分界线
plt.plot(x_boundary, y_boundary, 'g--', linewidth=2, label='非线性分界线')

# 设置图形属性
plt.xlabel('X 坐标')
plt.ylabel('Y 坐标')
plt.title('非线性分布的苹果树和橙子树')
plt.legend()
plt.grid(True, alpha=0.3)
plt.axis([0, 6, 0, 5])  # 设置坐标轴范围
plt.gca().set_aspect('equal')  # 确保坐标轴等比例
plt.tight_layout()
plt.show()

# 为了更好地展示非线性可分性，我们再画一个版本，使用更复杂的分布
plt.figure(figsize=(10, 8))

# 重新绘制树的位置
plt.scatter(A[:, 0], A[:, 1], s=300, c='red', marker='^', label='苹果树', edgecolors='darkred')
plt.scatter(O[:, 0], O[:, 1], s=300, c='orange', marker='o', label='橙子树', edgecolors='darkorange')

# 添加可能的圆形分界线
circle_center = [2.5, 2.5]
circle_radius = 1.5
circle_x = circle_center[0] + circle_radius * np.cos(np.linspace(0, 2*np.pi, 100))
circle_y = circle_center[1] + circle_radius * np.sin(np.linspace(0, 2*np.pi, 100))
plt.plot(circle_x, circle_y, 'b--', linewidth=2, label='圆形分界线')

# 填充圆形区域内部
plt.fill(circle_x, circle_y, 'blue', alpha=0.1)

# 设置图形属性
plt.xlabel('X 坐标')
plt.ylabel('Y 坐标')
plt.title('非线性分布 - 可能需要圆形边界')
plt.legend()
plt.grid(True, alpha=0.3)
plt.axis([0, 6, 0, 5])
plt.gca().set_aspect('equal')
plt.tight_layout()
plt.show()

5.SVM处理非线性问题

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 创建非线性分布数据
np.random.seed(42)

# 苹果树 (A) - 在圆形区域内的数据点
theta = np.linspace(0, 2*np.pi, 20)
r = 2 + 0.5*np.random.randn(20)
A = np.column_stack([r*np.cos(theta), r*np.sin(theta)])

# 橙子树 (O) - 在环形区域内的数据点
theta_o = np.linspace(0, 2*np.pi, 30)
r_o = 3.5 + 0.5*np.random.randn(30)
O = np.column_stack([r_o*np.cos(theta_o), r_o*np.sin(theta_o)])

# 创建标签数据
X = np.vstack([A, O])
y = np.array([0]*len(A) + [1]*len(O))  # 0表示苹果树，1表示橙子树

# 创建3个子图
fig = plt.figure(figsize=(18, 6))

# 第一个子图：原始二维空间
ax1 = plt.subplot(1, 3, 1)
ax1.scatter(A[:, 0], A[:, 1], s=300, c='red', marker='^', label='苹果树', edgecolors='darkred')
ax1.scatter(O[:, 0], O[:, 1], s=300, c='orange', marker='o', label='橙子树', edgecolors='darkorange')
ax1.set_xlabel('X 坐标')
ax1.set_ylabel('Y 坐标')
ax1.set_title('1. 原始二维空间：混在一起')
ax1.grid(True, alpha=0.3)
ax1.legend()
ax1.axis([-6, 6, -6, 6])

# 第二个子图：升维到三维空间
ax2 = plt.subplot(1, 3, 2, projection='3d')
# 通过RBF核函数模拟升维效果
r_sq = X[:, 0]**2 + X[:, 1]**2
z = np.exp(-0.1*r_sq)  # 高斯核函数效果
ax2.scatter(A[:, 0], A[:, 1], z[:len(A)], s=300, c='red', marker='^', label='苹果树', edgecolors='darkred')
ax2.scatter(O[:, 0], O[:, 1], z[len(A):], s=300, c='orange', marker='o', label='橙子树', edgecolors='darkorange')
ax2.set_xlabel('X 坐标')
ax2.set_ylabel('Y 坐标')
ax2.set_zlabel('Z 坐标（新特征）')
ax2.set_title('2. 升维到三维空间：可以平面分开')

# 添加一个分界平面示意
xx, yy = np.meshgrid(np.linspace(-6, 6, 10), np.linspace(-6, 6, 10))
zz = np.full_like(xx, 0.5)
ax2.plot_surface(xx, yy, zz, alpha=0.3, color='gray')
ax2.legend()

# 第三个子图：回到二维空间的曲线边界
ax3 = plt.subplot(1, 3, 3)

# 使用SVM训练一个非线性分类器
svm = SVC(kernel='rbf', gamma=0.5, C=1)
svm.fit(X, y)

# 创建网格点
xx, yy = np.meshgrid(np.linspace(-6, 6, 100), np.linspace(-6, 6, 100))
Z = svm.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 绘制决策边界
ax3.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
ax3.scatter(A[:, 0], A[:, 1], s=300, c='red', marker='^', label='苹果树', edgecolors='darkred')
ax3.scatter(O[:, 0], O[:, 1], s=300, c='orange', marker='o', label='橙子树', edgecolors='darkorange')
ax3.set_xlabel('X 坐标')
ax3.set_ylabel('Y 坐标')
ax3.set_title('3. 回到二维空间：优雅的曲线边界')
ax3.grid(True, alpha=0.3)
ax3.legend()
ax3.axis([-6, 6, -6, 6])

plt.tight_layout()
plt.show()

机器学习入门＜5＞支持向量机形象教学：寻找最安全的“三八线”，人人都能懂的算法核心

一、 引言

二、 核心目标：这堂课你就能明白的三件事

三、 第一部分：生活中的"分界"难题------公平的起点

1. 故事场景：土地划分的智慧

2. 对比实验：三条分界线的命运

四、 第二部分：核心概念解剖------从一条线到两条街

1. 可视化演示：SVM画的不只是一条线

2. "支持向量"------决定大局的少数关键点

五、 第三部分：为什么"最大间隔"如此重要？

1. 泛化能力测试：新树来了怎么办？

2. 现实世界类比

六、 第四部分：非线性情况------"空中俯视"的魔法

1. 难题出现：混在一起的圈子

2. 升维思考：从地面飞到空中

3. 回到地面：曲线诞生了

七、总结升华：SVM的哲学与三板斧

1. 全过程比喻回顾

2. 核心思想三句话

3. 极简代码感知

八、使用到的代码

1.苹果树与橙子树的地图

2.对比实验：三条分界线的绘制

3.SVM分割橘子树和苹果数的分布

4.橘子树和苹果数的非线性分布

5.SVM处理非线性问题

一、引言

二、核心目标：这堂课你就能明白的三件事

三、第一部分：生活中的"分界"难题------公平的起点

四、第二部分：核心概念解剖------从一条线到两条街

五、第三部分：为什么"最大间隔"如此重要？

六、第四部分：非线性情况------"空中俯视"的魔法