数据结构--初始数据结构

一、集合框架

1、什么是集合框架

Java集合框架(Java Collection Framework),又被称为容器(container),是定义在java.util包下的一组接口(interfaces)和其实现类(classes).

主要表现为把多个元素(element)放在一个单元中,用于对这些元素进行快速、便捷的存储（store）、检索（retrieve）、管理（manipulate），即平时俗称的增删改查（CRUD）

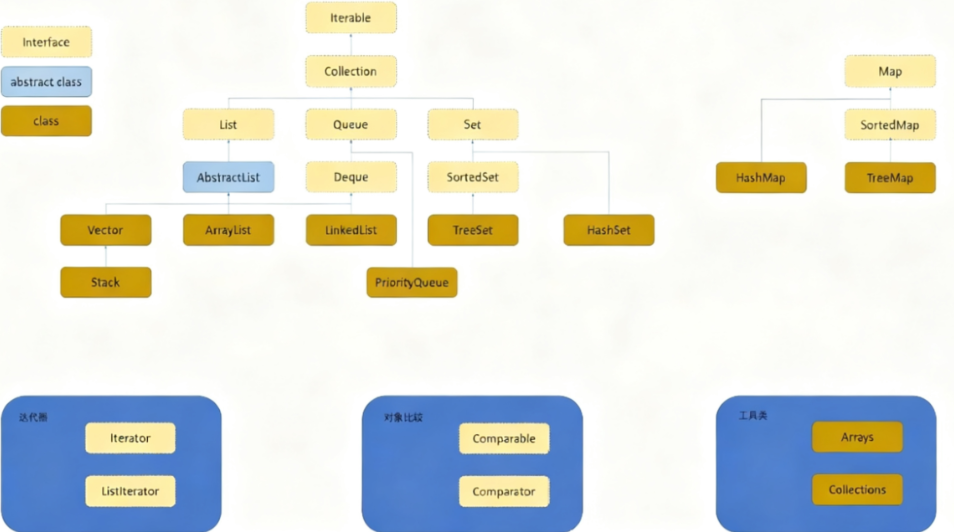
类和接口总览：

2、集合框架的重要性

2.1开发中的使用

（1）使用成熟的集合框架，有助于我们便捷、快速的写出高效、稳定的代码

（2）学习背后的数据结构知识，有助于我们理解各个集合的优缺点及使用场景

2.2笔试及面试题

在各厂的秋招中，常会用数据结构作为笔试的考题；不仅如此，哪怕是在面试中，也常常会问到我们一些数据结构相关的问题！！！

3、背后涉及的数据结构以及算法

3.1什么是数据结构

数据结构（Data Structure）是计算机存储、组织数据的方式，指互相之间存在一种或多种特定关系的数据元素的集合

3.2容器背后对应的数据结构

在这里，我们主要学习以下容器，每个容器其实都是对某种特定数据结构的封装，大概了解一下，后序会给大家详细讲解并模拟实现：

（1）Collection：一个接口，包含了大部分容器常用的一些方法

（2）List：一个接口，规范了ArrayList和LinkedList中要实现的方法

ArrayList：实现了List接口，底层为动态类型顺序表

LinkedList：实现了List接口，底层为双向链表

（3）Stack：底层是栈，栈是一种特殊的顺序表

（4）Queue：底层是队列，队列是一种特殊的顺序表

（5）Deque：是一个接口

（6）Set：集合，是一个接口，里面放置的是K模型

HashSet：底层为哈希桶，查询的时间复杂度为O(1)

TreeSet：底层为红黑树，查询的时间复杂度为O( logN ),关于key有序的

（7）Map：映射，里面存储的是K-V模型的键值对

HashMap：底层为哈希桶，查询时间复杂度为O(1)

TreeMap：底层为红黑树，查询的时间复杂度为O(logN)，关于key有序

3.3相关java知识

（1）泛型（Generic）

（2）自动装箱（autobox）和自动拆箱（autounbox）

（3）Object 的 equals 方法

（4）Comparable 和 Comparator 接口

3.4什么是算法

算法(Algorithm):就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果。

3.5如何学好数据结构以及算法

不少人都会问：怎么才能学会学好数据结构呢？？？

(1)死磕代码，磕成这样就可以了

（2）注意画图和思考

在我看来，学数据结构主要分为这样的过程：

思考==>画图==>写代码（N）==>画图==>再次写代码==>调试==>......

#注：一定要画图！！！一定要画图！！！一定要画图！！！

（3）多看两遍我的博客或者自己写点的东西（如博客），多做总结

（4）多刷题

可以在牛客网和LeetCode上面刷一下相关的数据结构，看一下不同的解题思路！！！

1、时间和空间复杂度

首先要明确，我们不只是说只要可以实现、完成任务就可以，而是要尽可能用更少的时间、更少的空间来完成任务！！！（就像是干活一样，不仅要老板满意，还要在保证质量的情况下用最短的时间以及最少的成本完成工作，让利益最大化！！！）

1、算法的效率

算法效率分析分为两种：第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率被称作空间复杂度。时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间

（在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。但是，一些面试题或者笔试题中有要求！！！）

2、时间复杂度

2.1时间复杂度的概念

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个数学函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

2.2大O的渐进表示法

java 复制代码

 // 请计算一下func1基本操作执行了多少次？
 void func1(int N){
     int count = 0;
     for (int i = 0; i < N ; i++) {
         for (int j = 0; j < N ; j++) {
             count++;
         }
     }//N^2
     for (int k = 0; k < 2 * N ; k++) {
          count++;
     }//2*N
     int M = 10;
     while ((M--) > 0) {
          count++;
     }//10
     System.out.println(count);
 }

Func1 执行的基本操作次数：

F（N） = N^2 + 2*N + 10

（1）N = 10 F(N) = 130

（2）N = 100 F(N) = 10210

（3）N = 1000 F(N) = 1002010

实际我们计算时间复杂度时，我们只需要算大概执行的次数，也就是大O的渐进表示法

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

2.3推导大O阶方法

第一步：确定 "基本操作"（算法的核心执行单元）

基本操作是算法中执行次数最多、最能代表 "耗时" 的语句（通常是循环内的核心代码、数组访问、算术运算等）。

第二步：计算基本操作的 "执行次数函数"`F(N)`

统计基本操作会被执行多少次，这个次数是输入规模N的函数（比如F(N) = 2N + 3、F(N) = N² + 5N + 10）。

第三步：按 3 条规则化简`F(N)`，得到大 O 表示

无论F(N)多复杂，只需 3 步就能化简为标准大 O 形式，核心是 "去掉对增长趋势无影响的部分"：

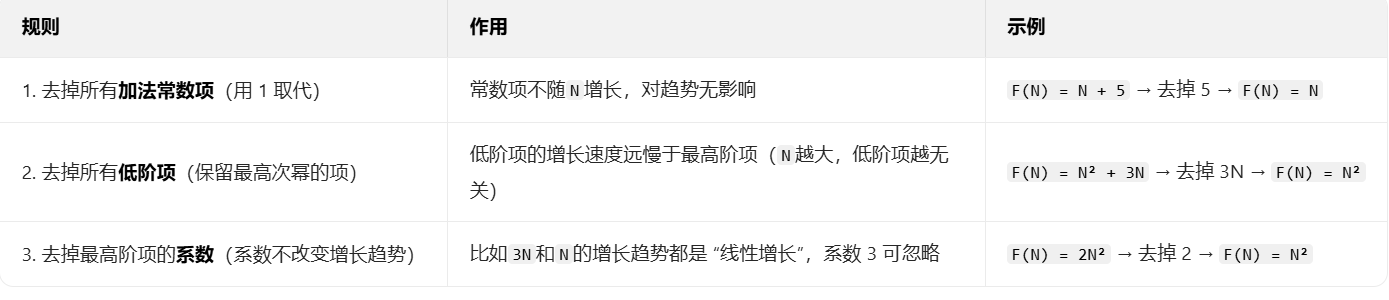
（1）用常数1取代运行时间中的所有加法常数（换常数）

（2）在修改后的运行次数函数中，只保留最高阶项（只保留最高相）

（3）如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。（系数变成1）

使用大O的渐进表示法以后，Func1的时间复杂度为：O（N^2）

（1）N = 10 F(N) = 100

（2）N = 100 F(N) = 10000

（3）N = 1000 F(N) = 1000000

通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。另外有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数(上界)（最慢）

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数(下界)（最快）

如：在一个长度为N数组中搜索一个数据x

最好情况：1次找到

最坏情况：N次找到

平均情况：N/2次找到

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

实例：

2、实战示例（覆盖 90% 日常场景）

下面用最常见的代码场景，演示如何套用 3 步走计算复杂度：

场景 1：O (1)（常数复杂度，与 N 无关）

特点：基本操作的执行次数固定，不随N变化（无论N是 10 还是 10000，执行次数都一样）。

代码示例（数组访问、简单运算）

java 复制代码

// 从数组中获取第k个元素（k固定）
int getElement(int[] arr, int k) {
    return arr[k]; // 基本操作：数组访问，仅执行1次
}

// 两个数相加（无论a、b多大，执行次数固定）
int add(int a, int b) {
    int sum = 0; // 1次
    sum = a + b; // 1次
    return sum; // 1次
}

计算过程：

基本操作：数组访问 / 加法运算，执行次数F(N) = 1（或 3，无关）；
化简：按规则 1，常数项用 1 取代 → F(N) = 1；无低阶项、系数为 1 → 最终复杂度O(1)。

关键：

所有 "不依赖输入规模N" 的操作，复杂度都是O(1)（比如哈希表的get/put、栈的push/pop，理想情况下）。

场景 2：O (N)（线性复杂度，随 N 线性增长）

特点：基本操作的执行次数与N成正比（N翻倍，执行次数也翻倍）。

代码示例（单循环遍历）

java 复制代码

// 遍历数组，统计偶数个数（N是数组长度）
int countEven(int[] arr) {
    int count = 0; // 1次（常数项）
    for (int i = 0; i < arr.length; i++) { // 循环N次
        if (arr[i] % 2 == 0) { // 基本操作：判断偶数，执行N次
            count++; // 最多执行N次，仍算O(N)
        }
    }
    return count; // 1次（常数项）
}

计算过程：

基本操作：arr[i] % 2 == 0（循环内核心判断），执行次数F(N) = N；
其他操作（count 初始化、return）都是常数项，按规则 1 忽略；
化简后：O(N)。

关键：

单重循环 （无论循环内有多少行代码，只要不嵌套其他循环），复杂度通常是O(N)。

场景 3：O (N²)（平方复杂度，随 N 平方增长）

特点：基本操作的执行次数与N²成正比（N翻倍，执行次数翻 4 倍），常见于嵌套循环 （外层循环N次，内层循环也N次）。

代码示例（双层嵌套循环）

java 复制代码

// 冒泡排序（N是数组长度）
void bubbleSort(int[] arr) {
    for (int i = 0; i < arr.length; i++) { // 外层循环：N次
        for (int j = 0; j < arr.length - i - 1; j++) { // 内层循环：最多N次
            if (arr[j] > arr[j+1]) { // 基本操作：元素比较，执行N*N次
                int temp = arr[j]; // 交换操作，最多N*N次
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
}

计算过程：

基本操作：arr[j] > arr[j+1]（嵌套循环内核心比较）；
执行次数：外层循环N次，内层循环平均N/2次 → 总次数F(N) = N * (N/2) = 0.5N²；
化简：按规则 3 去掉系数 0.5 → F(N) = N² → 最终复杂度O(N²)。

关键：

k 层嵌套循环 （每层循环次数与N成正比），复杂度通常是O(Nᵏ)（比如 3 层嵌套是O(N³)）。

场景 4：O (logN)（对数复杂度，增长极慢）

特点：基本操作的执行次数与N的对数成正比（N翻倍时，执行次数只加 1），常见于 "每次缩小一半规模" 的算法（如二分查找、二叉树遍历）。

代码示例（二分查找）

java 复制代码

// 从有序数组中查找目标值（N是数组长度）
int binarySearch(int[] arr, int target) {
    int left = 0, right = arr.length - 1;
    while (left <= right) { // 循环次数：log₂N次
        int mid = (left + right) / 2; // 基本操作：计算中间索引
        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] > target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return -1;
}

计算过程：

每次循环，查找范围缩小一半（从N→N/2→N/4→...→1）；
循环次数：需要log₂N次才能缩小到 1（比如N=8时，循环 3 次；N=16时，循环 4 次）；
基本操作执行次数F(N) = log₂N，化简后复杂度O(logN)（对数的底数不影响趋势，可省略）。

场景 5：O (NlogN)（线性对数复杂度，常用排序算法）

特点：基本操作的执行次数是N * logN（N线性增长，logN对数增长，结合后比O(N²)高效得多），常见于高效排序算法（如快速排序、归并排序、堆排序）。

代码逻辑（归并排序核心）

归并排序的思路是 "分治"：

把数组分成两半（分：logN层，每层分 2 份，共分logN次）；
每层合并两个有序数组（合：每层需要N次操作，因为所有元素都要合并一次）；
总执行次数：logN层 × 每层N次 = NlogN。

复杂度：

F(N) = NlogN → 化简后O(NlogN)。

场景 6：并列循环（取最高阶，不叠加）

特点：多个循环并列（不是嵌套）时，复杂度取 "最高阶的那个"，不是所有循环次数相加。

代码示例

java 复制代码

void test(int[] arr) {
    // 循环1：O(N)
    for (int i = 0; i < arr.length; i++) {
        System.out.println(arr[i]);
    }
    // 循环2：O(N²)
    for (int i = 0; i < arr.length; i++) {
        for (int j = 0; j < arr.length; j++) {
            System.out.println(arr[i] + arr[j]);
        }
    }
}

计算过程：

执行次数F(N) = N + N²；
按规则 2，保留最高阶项N²，去掉低阶项N → 最终复杂度O(N²)。

3、常见复杂度排序（从高效到低效）

日常开发中遇到的复杂度，增长速度排序如下（N越大，差距越明显）：O(1) < O(logN) < O(N) < O(NlogN) < O(N²) < O(N³) < O(2ⁿ)（指数级，极低效）

高效算法：O(1)（哈希表操作）、O(logN)（二分查找）、O(N)（单循环）、O(NlogN)（快速排序）；
低效算法：O(N²)（双层嵌套）、O(2ⁿ)（递归求斐波那契，无优化），尽量避免在N较大时使用。

4、避坑关键点

只看 "增长趋势"，不看具体次数 ：比如F(N) = 1000N和F(N) = N，复杂度都是O(N)（1000 是系数，可忽略）；F(N) = N² + 10000和F(N) = N²，复杂度都是O(N²)（10000 是常数项，可忽略）。
嵌套循环≠O (N²) ：只有 "每层循环次数都与N成正比" 才是O(N²)；如果内层循环次数是固定值（比如for (int j = 0; j < 10; j++)），复杂度是O(N)（固定次数的循环属于常数项）。
递归算法看 "递归深度" 和 "每层操作次数" ：比如递归版二分查找（深度logN，每层操作O(1)）→ O(logN)；递归版归并排序（深度logN，每层操作O(N)）→ O(NlogN)。

2.4常见的时间复杂度计算举例

实例1：

java 复制代码

void func3(int N, int M) {
    int count = 0; 
    for (int k = 0; k < M; k++) {
        count++;//M
    } 
    for (int k = 0; k < N ; k++) {
        count++;//N
    } 
    System.out.println(count);
 }

由于基本操作执行了N+M次，并且两数都是未知数，所以时间复杂度为O（N+M）

实例2：

java 复制代码

void bubbleSort(int[] array) {
    for (int end = array.length; end > 0; end--) {
        boolean sorted = true;
        for (int i = 1; i < end; i++) {
            if (array[i - 1] > array[i]) {
                Swap(array, i - 1, i);
                sorted = false;
            }//N*(N-1)/2
        } 
        if (sorted == true) {
            break;
        }
    }
 }

由于循环执行，第一次执行（N-1）次，最后一次执行了0次，共N次，求每次比前一次少一次，因此得到N*(N-1)/2，因此时间复杂度为O(N^2)

实例三：

java 复制代码

int binarySearch(int[] array, int value) {
    int begin = 0;
    int end = array.length - 1;
    while (begin <= end) {
        int mid = begin + ((end-begin) / 2);
        if (array[mid] < value)
            begin = mid + 1;
        else if (array[mid] > value)
            end = mid - 1;
        else
            return mid;
    }
    return -1;
 }

二分查找，一次是原来的一半可以得出（N/2）^O=1,计算可得时间复杂度为O（logN）(logN是以2为底，lgN是以10为底)

实例四：

java 复制代码

 long factorial(int N) {
    return N < 2 ? N : factorial(N-1) * N;
 }

阶乘递归是在比较N和2的大小关系进行选择，可以发现共递归了N次，所以时间复杂度为O(N)

实例五：

java 复制代码

 int fibonacci(int N) {
    return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
 }

我们可以发现，左侧最顶端（第一次）是（N-1）,最后一次是1，也就可以得到近似的1+2^1+......+2^（N-1）,也就是2^N-1,同理，右侧也可以计算出是2^(N-1)-1，因此时间复杂度为O(2^N)

我们常遇到的复杂度有：O(1) < O(logN) < O(N) < O(N*logN) < O(N^2)

三、空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似，也使用大O渐进表示法。

实例一：

java 复制代码

void bubbleSort(int[] array) {
    for (int end = array.length; end > 0; end--) {
        boolean sorted = true;
        for (int i = 1; i < end; i++) {
            if (array[i - 1] > array[i]) {
                Swap(array, i - 1, i);
                sorted = false;
            }
        }
        if (sorted == true) {
            break;
        }
    }
}

因为使用了常数个额外空间，所以空间复杂度为O(1)

实例二：

java 复制代码

int[] fibonacci(int n) {
     long[] fibArray = new long[n + 1];
     fibArray[0] = 0;
     fibArray[1] = 1;
     for (int i = 2; i <= n ; i++) {
         fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
     }
     return fibArray;
 }

因为动态开辟了N个空间，空间复杂度为 O(N）

实例三：

java 复制代码

 long factorial(int N) {
     return N < 2 ? N : factorial(N-1)*N;
 }

因为递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间，因此空间复杂度为O(N）

三、包装类

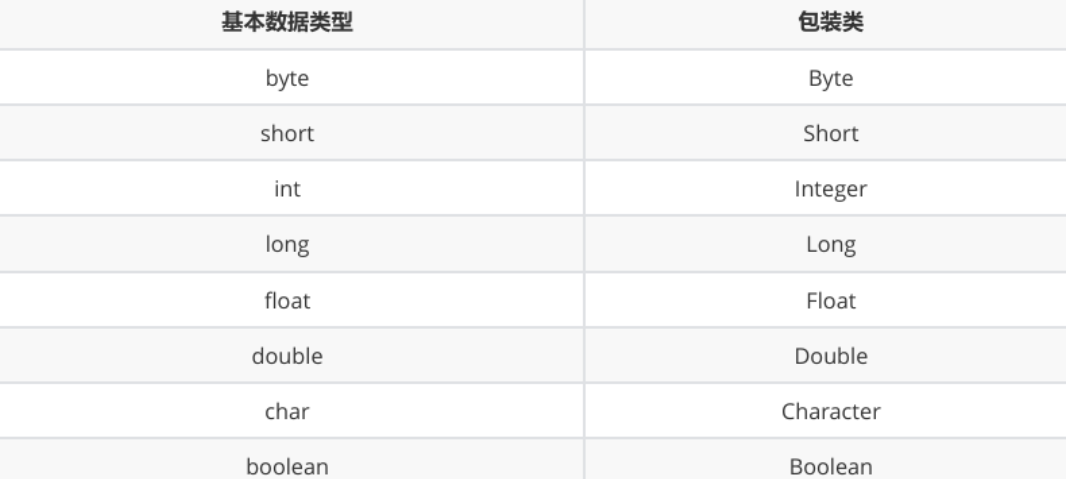
在Java中，由于基本类型不是继承自Object，为了在泛型代码中可以支持基本类型，Java给每个基本类型都对应了一个包装类型。

1、基本数据类型和对应的包装类

2、装箱和拆箱

装箱（Boxing）：将「基本数据类型」转换为对应的「包装类对象」；
拆箱（Unboxing）：将「包装类对象」转换为对应的「基本数据类型」。

Java 5+ 支持 自动装箱（Auto-Boxing） 和 自动拆箱（Auto-Unboxing）

3、自动装箱和自动拆箱

我们可以看到在使用过程中，装箱和拆箱带来不少的代码量，所以为了减少开发者的负担，java 提供了自动机制。

底层仍会调用包装类的方法，但无需开发者手动编写，代码更简洁。

1. 自动装箱（基本类型 → 包装类）

当需要包装类对象时，编译器自动将基本类型转换为包装类。

常见场景 + 示例：

java 复制代码

// 场景1：直接赋值（基本类型 → 包装类）
Integer num1 = 10; // 自动装箱：等价于 Integer num1 = Integer.valueOf(10);
Boolean flag = true; // 自动装箱：等价于 Boolean flag = Boolean.valueOf(true);

// 场景2：基本类型作为集合元素（集合只能存对象，自动装箱）
List<Integer> list = new ArrayList<>();
list.add(20); // 自动装箱：int 20 → Integer 对象，再存入集合

// 场景3：方法参数为包装类，传入基本类型
public static void print(Integer x) {
    System.out.println(x);
}
print(30); // 自动装箱：int 30 → Integer 对象

2. 自动拆箱（包装类 → 基本类型）

当需要基本类型时，编译器自动将包装类对象转换为基本类型。

常见场景 + 示例：

java 复制代码

// 场景1：直接赋值（包装类 → 基本类型）
Integer num2 = Integer.valueOf(40);
int x = num2; // 自动拆箱：等价于 int x = num2.intValue();

// 场景2：包装类参与算术运算（自动拆箱为基本类型后计算）
Integer a = 5;
Integer b = 10;
int sum = a + b; // 自动拆箱：a→int 5，b→int 10，再相加

// 场景3：方法返回值为包装类，接收为基本类型
public static Integer getNum() {
    return 60; // 先自动装箱为 Integer
}
int y = getNum(); // 自动拆箱：Integer → int

三、手动装箱与拆箱（底层实现，了解即可）

自动装箱 / 拆箱的底层本质是调用包装类的方法，手动调用这些方法就是「手动装箱 / 拆箱」，适用于需要精确控制转换的场景。

java 复制代码

// 1. 手动装箱（int → Integer）
int basic = 100;
Integer wrapper = Integer.valueOf(basic); // 手动装箱

// 2. 手动拆箱（Integer → int）
int basic2 = wrapper.intValue(); // 手动拆箱

// 其他类型示例（double ↔ Double）
double d = 3.14;
Double dWrapper = Double.valueOf(d); // 手动装箱
double dBasic = dWrapper.doubleValue(); // 手动拆箱

四、核心注意事项（避坑重点！）

1. 空指针异常（最常见坑）

包装类是对象，可能为 null；而拆箱时会调用 xxxValue() 方法，若包装类对象为 null，会直接抛出 NullPointerException。

java 复制代码

Integer num = null;
// int val = num; // 报错：NullPointerException（自动拆箱时num为null）

// 正确写法：先判断非null
if (num != null) {
    int val = num; // 安全拆箱
}

2. 包装类的缓存机制（高频考点）

为了优化性能，Java 对部分包装类（Integer、Short、Byte、Character、Long）,的「常用值范围」做了缓存：(浮点和布尔的没有缓存机制)

缓存范围：-128 ~ 127（Integer 可通过 JVM 参数 -XX:AutoBoxCacheMax 调整上限）；
当装箱的值在缓存范围内时，直接返回缓存中的对象；超出范围则新建对象。

数据结构--初始数据结构

一、集合框架

1、什么是集合框架

2.1开发中的使用

2.2笔试及面试题

3、背后涉及的数据结构以及算法

3.1什么是数据结构

3.2容器背后对应的数据结构

3.3相关java知识

3.4什么是算法

3.5如何学好数据结构以及算法

1、时间和空间复杂度

1、算法的效率

2、时间复杂度

2.1时间复杂度的概念

2.2大O的渐进表示法

2.3推导大O阶方法

第一步：确定 "基本操作"（算法的核心执行单元）

第二步：计算基本操作的 "执行次数函数"F(N)

第三步：按 3 条规则化简F(N)，得到大 O 表示

2、实战示例（覆盖 90% 日常场景）

场景 1：O (1)（常数复杂度，与 N 无关）

代码示例（数组访问、简单运算）

计算过程：

关键：

场景 2：O (N)（线性复杂度，随 N 线性增长）

代码示例（单循环遍历）

计算过程：

关键：

场景 3：O (N²)（平方复杂度，随 N 平方增长）

代码示例（双层嵌套循环）

计算过程：

关键：

场景 4：O (logN)（对数复杂度，增长极慢）

代码示例（二分查找）

计算过程：

场景 5：O (NlogN)（线性对数复杂度，常用排序算法）

代码逻辑（归并排序核心）

复杂度：

场景 6：并列循环（取最高阶，不叠加）

代码示例

计算过程：

3、常见复杂度排序（从高效到低效）

4、避坑关键点

2.4常见的时间复杂度计算举例

三、包装类

1、基本数据类型和对应的包装类

2、装箱和拆箱

3、自动装箱和自动拆箱

1. 自动装箱（基本类型 → 包装类）

常见场景 + 示例：

2. 自动拆箱（包装类 → 基本类型）

常见场景 + 示例：

三、手动装箱与拆箱（底层实现，了解即可）

四、核心注意事项（避坑重点！）

1. 空指针异常（最常见坑）

2. 包装类的缓存机制（高频考点）

第二步：计算基本操作的 "执行次数函数"`F(N)`

第三步：按 3 条规则化简`F(N)`，得到大 O 表示