2025.12.6 论文阅读

一、文献阅读

一、文献阅读

题目信息

题目：《Quantum Long Short-Term Memory》

期刊： IEEE

作者： Samuel Yen-Chi Chen, Shinjae Yoo, and Yao-Lung L. Fang

发表时间： 2020

文章链接： https://arxiv.org/pdf/2009.01783

摘要

本文提出了一种混合量子-经典模型 QLSTM，通过使用变分量子电路替换经典LSTM单元中的神经网络层，成功将架构扩展到了量子领域。实验表明，在参数数量相似的情况下，QLSTM在学习多种时间序列数据时，比经典模型收敛速度更快，所需的训练轮次更少，且收敛过程更加稳定。由于采用变分方法，该模型对量子比特数和电路深度的要求较低，非常适合在当前的含噪中等规模量子设备上实现。

创新点

作者首创将变分量子电路引入 LSTM 架构，替代了经典单元中遗忘门、输入门、更新层和输出门里的线性变换层，从而利用量子纠缠特性增强模型的表达能力。

在数据处理上，作者提出了一种基于反正切函数的量子编码方案。这种设计不仅能适应任意实数域输入，还通过引入平方项 x 2 x^2 x2 增加了高阶非线性特征。此外，作者还Parameter-shift 规则实现了混合架构下的解析梯度计算，使得量子电路可以像经典神经网络一样通过反向传播算法进行高效训练。从实验效果来看，QLSTM 展现出了显著的收敛性与稳定性优势。即便在参数量相当甚至更少的情况下，模型在训练初期就能提取到更多有效信息，且损失函数下降曲线平滑，没有出现经典 LSTM 常见的尖峰波动。

网络框架

文章构建的混合序列建模框架，核心在于用变分量子电路 VQC 替换了原有的矩阵乘法操作。

变分量子电路模块

VQC 是模型的基本构建块，由三个部分串联而成：

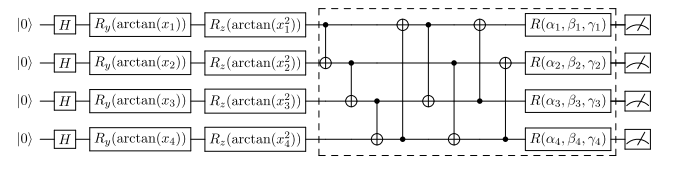
数据编码层，将经典输入向量 v ⃗ \vec{v} v 编码为量子态。使用 H 门制备叠加态后，通过旋转门 R y R_y Ry 和 R z R_z Rz 进行编码，角度由输入数据及其平方值的反正切函数决定。
变分层，由一系列用于产生纠缠的 CNOT 门和单量子比特旋转门组成，其中的旋转角度即为网络的可训练参数。
量子测量层，通过测量量子比特在计算基下的期望值，将量子态转换回经典标量，供后续的非线性激活函数使用。

QLSTM 单元架构

QLSTM 单元通过堆叠多个 VQC 构建而成。如下图所示，黄框部分为单元主体，蓝色小块即为上述的 VQC 模块。

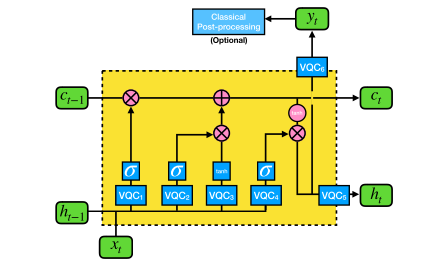
输入向量 v t v_t vt 由上一时刻的隐藏状态 h t − 1 h_{t-1} ht−1 和当前输入 x t x_t xt 拼接而成。

单元内部的逻辑如下：

遗忘门 f t f_t ft 通过 V Q C 1 VQC_1 VQC1 处理，决定保留多少旧的细胞状态 c t − 1 c_{t-1} ct−1；

输入门 i t i_t it 通过 V Q C 2 VQC_2 VQC2 处理，决定更新哪些新信息；

候选态 C ~ t \tilde{C}_t C~t 由 V Q C 3 VQC_3 VQC3 生成新的候选记忆；

细胞状态 c t c_t ct 结合遗忘门和输入门的结果进行更新；

输出门 o t o_t ot 由 V Q C 4 VQC_4 VQC4 控制；

最终输出为了匹配维度，作者额外增加了 V Q C 5 VQC_5 VQC5 和 V Q C 6 VQC_6 VQC6 分别生成隐藏状态 h t h_t ht 和最终输出 y t y_t yt。

实验结果

为了公平比较，作者构建了参数量相近的经典 LSTM与 QLSTM进行对比，实验基于 PyTorch 和 PennyLane 模拟环境。

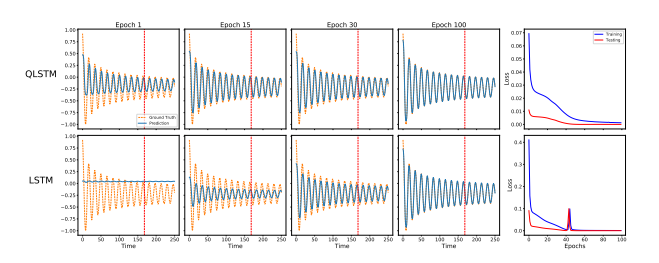
实验一：在学习正弦函数 y = sin ⁡ ( x ) y=\sin(x) y=sin(x) 的任务中，QLSTM 在第1个 Epoch 就展现了极佳的拟合效果，学到的信息显著多于经典模型。到第15个 Epoch 时，其训练 Loss 明显更低，且收敛曲线非常平滑，没有出现经典模型中常见的震荡。

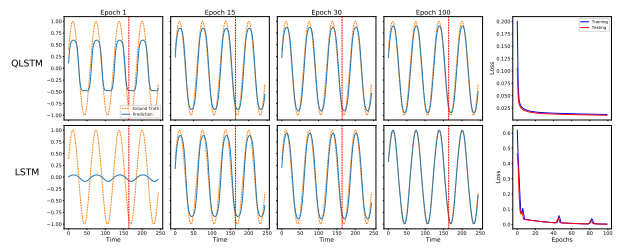
实验二：在预测阻尼谐振子角速度的任务中，QLSTM 不仅收敛更快，而且在极值点处的拟合更加温和精准，避免了经典 LSTM 容易出现的过冲现象。

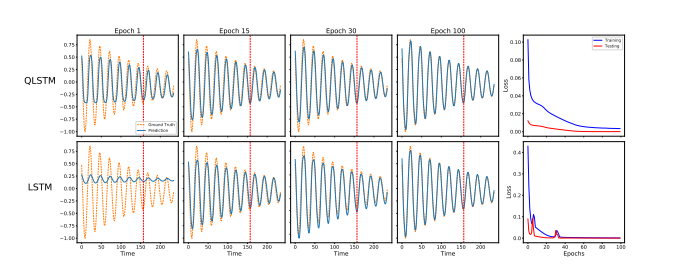
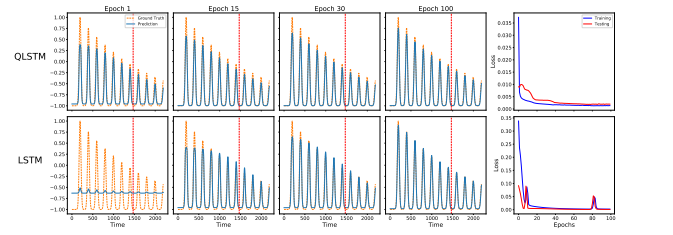
实验三：针对非指数衰减的复杂函数 J 2 ( x ) J_2(x) J2(x)，经典 LSTM 在训练初期几乎失效，预测结果呈平直线；而 QLSTM 迅速捕捉到了复杂的震荡模式，展现了强大的非线性学习能力。

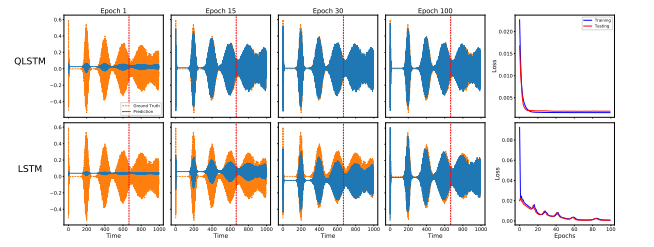
实验四：在预测延迟量子控制和种群反转任务中，QLSTM 同样表现出色。特别是在种群反转任务中，当系统处于基态激发态平衡（ D = 0 D=0 D=0）时，经典 LSTM 难以学习到零偏置特征，产生了较大误差，而 QLSTM 则能准确预测这一物理现象。

结论

本文证明了 QLSTM 在处理时间序列数据上具有比经典 LSTM 更高的数据效率和稳定性。在同等参数规模下，它不仅收敛更快，而且能够更敏锐地捕捉数据的局部特征，尤其是在复杂的非线性动力学系统中表现优异。这也为在 NISQ 设备上利用量子机器学习解决气象预测、物理模拟等科学问题提供了理论基础。

不足与展望

尽管模型表现优异，但目前仍存在一些局限性。首先是模拟算力瓶颈，由于采用 Parameter-shift 方法计算梯度，每次更新需要大量的量子电路评估，导致在经典计算机上模拟训练极其耗时，难以扩展到大规模数据集。其次是理想环境假设，当前的实验均在无噪声的模拟环境下进行，未充分考虑真实量子硬件中的退相干和读取误差对记忆单元的影响。最后，编码方式相对固定，使用了固定的旋转门编码，未来可以探索振幅编码等更节省资源的方案。