0.前言
今晚在宿舍里,手机屏幕突然亮起,是同学发来的一道曲面积分题。题目不长,却包含了两组精致的几何对象:一组是平行平面 x+y+z=0 与 x+y+z=1 所夹的空间区域,另一组则是由直线绕空间对角线旋转生成的曲面。作为数学一的考生,我立刻被这道题吸引------它不仅考察计算技巧,更考验空间想象能力。
为什么我要专门为这道题写一篇博客?
因为在解题的过程中,我意识到许多同学面临的困境:我们擅长符号运算和公式推导,却往往在脑海中难以构建出题目所描述的三维几何结构。当题目描述"介于平面x+y+z=0与x+y+z=1之间的部分的外侧"时,你能立即在脑海中勾勒出这个区域吗?当它说"由直线{x=0,y=0}绕直线{x=t,y=t,z=t}旋转得到的曲面"时,你能否想象出这个旋转曲面的形状?
这正是数学可视化的重要性所在。
作为数学一考生,我深知多元函数积分学是重要考点,而曲面积分更是其中的难点。传统的学习方法往往停留在纸面推导,缺乏对几何意义的直观理解。当我们无法"看见"积分区域时,解题就变成了机械套用公式,一旦题目稍有变化,便束手无策。
这道题的精妙之处在于,它将两种不同方式定义的曲面结合在同一个问题中:一个由代数方程定义(平面束),一个由几何变换定义(旋转曲面)。理解它们之间的空间关系,是正确建立积分区域的关键。
于是我打开了MATLAB,决定将抽象的数学描述转化为可视化的三维图形。
在绘制这些曲面的过程中,一些原本模糊的概念变得清晰起来:
两个平行平面的法向量相同,它们之间的区域是一个等距的"夹层"
旋转曲面与这些平面的交线形成了复杂的空间曲线
积分区域的"外侧"方向在可视化后变得直观明了
这篇博客不仅记录了我的解题过程,更重要的是分享了如何利用MATLAB这一工具,将抽象的数学概念具象化。我相信,通过将代数方程转化为三维图形,我们能够:
加深对空间几何结构的理解
验证计算结果的合理性
培养将抽象问题可视化的思维能力
在数学一考研的征程中,这种几何直观能力与计算能力的结合,正是解决综合性大题的关键。希望这篇博客不仅能帮助我的同学理解这道具体的题目,更能提供一种学习方法------当数学公式变得难以捉摸时,不妨尝试将它画出来,让几何直觉指引你的思考。
让我们一同走进这个由平面与旋转曲面构成的奇妙空间,在可视化的帮助下,重新认识曲面积分的几何本质。
1.x+y+z=0三维曲面图
Matlab
% 方法3:使用fill3绘制有边界的平面
figure('Position', [100, 100, 800, 600]);
% 定义平面的四个角点
vertices = [
-5, -5, 10; % 点1
5, -5, 0; % 点2
5, 5, -10; % 点3
-5, 5, 0; % 点4
];
% 使用fill3绘制填充的四边形
fill3(vertices(:,1), vertices(:,2), vertices(:,3), [0.2, 0.6, 0.8], ...
'FaceAlpha', 0.6, 'EdgeColor', 'k', 'LineWidth', 2);
hold on;
% 添加坐标轴
xlim([-10 10]); ylim([-10 10]); zlim([-15 15]);
xlabel('X轴'); ylabel('Y轴'); zlabel('Z轴');
title('平面 x+y+z=0 (使用fill3绘制)');
grid on;
% 添加坐标系原点
plot3(0, 0, 0, 'ko', 'MarkerSize', 8, 'MarkerFaceColor', 'k');
% 添加平面上的线
t = linspace(-5, 5, 20);
line1_x = t;
line1_y = zeros(size(t));
line1_z = -t;
plot3(line1_x, line1_y, line1_z, 'r-', 'LineWidth', 2);
line2_x = zeros(size(t));
line2_y = t;
line2_z = -t;
plot3(line2_x, line2_y, line2_z, 'g-', 'LineWidth', 2);
legend('平面 x+y+z=0', '原点', 'x+z=0 (y=0)', 'y+z=0 (x=0)');
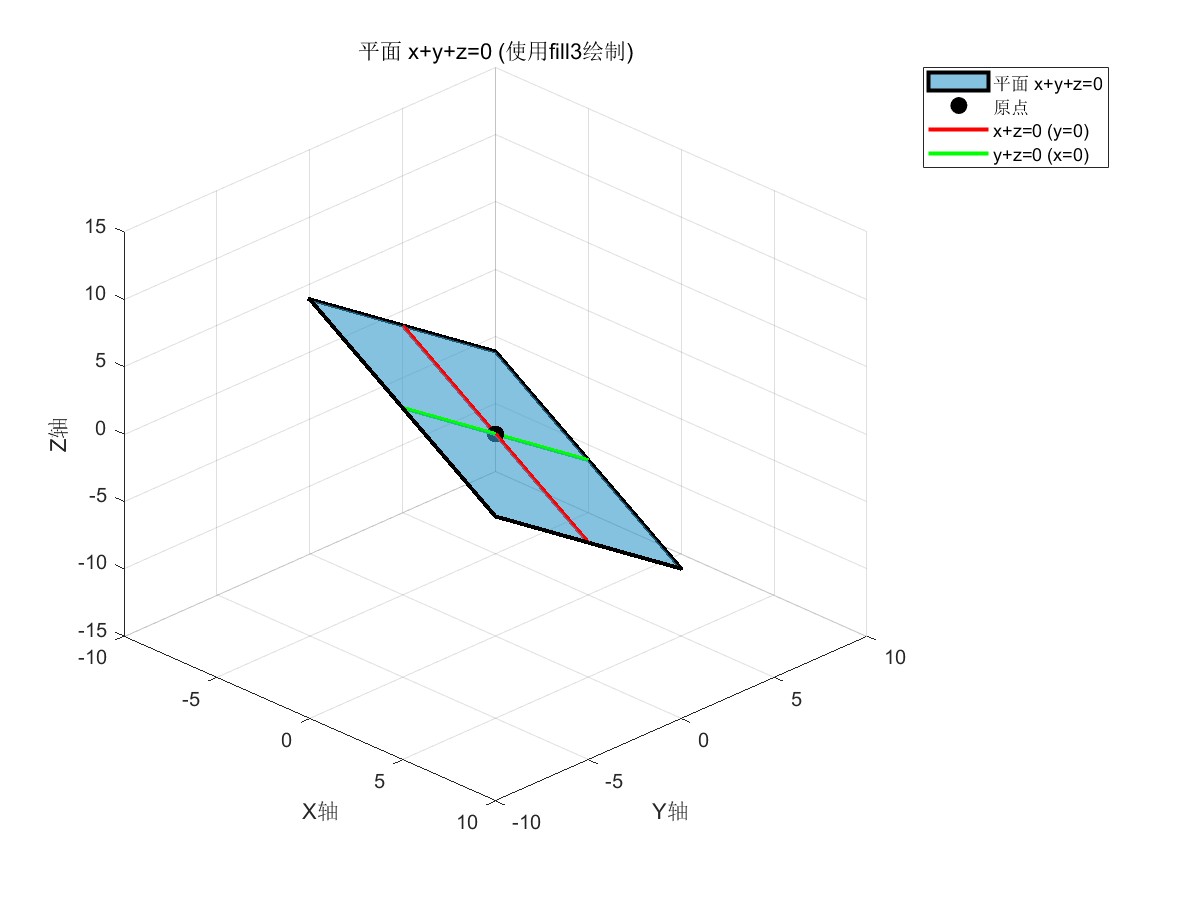
view(45, 30);这段代码使用 MATLAB 创建了一个包含自定义三维平面及辅助几何元素的可视化图形。其核心目标是绘制一个在三维空间中由四个角点定义的不规则四边形平面,并通过添加坐标线、原点和图例等方式,使其空间位置和方程式关系更加清晰直观。
具体而言,代码首先定义了一个图形的四角顶点坐标,这些顶点并不位于同一高度,因此形成了一个倾斜的平面。随后,它使用 fill3 函数以半透明的青蓝色填充这个四边形,并绘制了黑色的粗边以明确其边界。为了建立空间参考,代码设置了坐标轴范围、标签和网格,并在原点处绘制了一个黑色实心点。
最后,为了进一步阐明该平面的空间方位(接近平面 𝑥+𝑦+𝑧=0),代码在平面上叠加了两条特定的相交直线:一条是当𝑦=0时𝑥+𝑧=0的红色直线,另一条是当 𝑥=0时y+z=0的绿色直线。整个图形辅以图例,并设定了特定的三维视角以优化显示效果。
2.x+y+z=1三维曲面图
Matlab
%% 使用 fill3 绘制平面 x + y + z = 1
figure('Position', [100, 100, 800, 600], 'Name', '平面 x+y+z=1 (fill3绘制)');
% 定义边界:取平面在 x,y∈[-2,2] 范围内的部分
% 由于 z = 1 - x - y,我们需要确保 z 也在合理范围内
% 创建四个边界点,形成一个四边形区域
% 点1:x=2, y=-1 => z=0
% 点2:x=2, y=2 => z=-3
% 点3:x=-2, y=2 => z=1
% 点4:x=-2, y=-1 => z=4
vertices = [
2, -1, 0; % 点1
2, 2, -3; % 点2
-2, 2, 1; % 点3
-2, -1, 4; % 点4
];
% 使用 fill3 绘制填充的四边形
fill3(vertices(:,1), vertices(:,2), vertices(:,3), [0.8, 0.4, 0.2], ...
'FaceAlpha', 0.7, 'EdgeColor', 'k', 'LineWidth', 2);
hold on;
% 添加坐标轴
xlim([-3, 3]); ylim([-3, 3]); zlim([-4, 5]);
xlabel('X轴'); ylabel('Y轴'); zlabel('Z轴');
title('平面方程: x + y + z = 1 (使用fill3绘制)', 'FontSize', 14);
grid on;
% 添加平面与坐标轴的交点
plot3(1, 0, 0, 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
plot3(0, 1, 0, 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g');
plot3(0, 0, 1, 'bo', 'MarkerSize', 10, 'MarkerFaceColor', 'b');
text(1.2, 0, 0, '(1,0,0)', 'FontSize', 10);
text(0, 1.2, 0, '(0,1,0)', 'FontSize', 10);
text(0, 0, 1.2, '(0,0,1)', 'FontSize', 10);
% 添加平面与坐标平面的交线
% 与xy平面的交线:z=0 => x+y=1
t = linspace(-1, 2, 100);
x_line = t;
y_line = 1 - t;
z_line = zeros(size(t));
plot3(x_line, y_line, z_line, 'r-', 'LineWidth', 2);
% 与yz平面的交线:x=0 => y+z=1
y_line2 = t;
z_line2 = 1 - y_line2;
plot3(zeros(size(t)), y_line2, z_line2, 'g-', 'LineWidth', 2);
% 与xz平面的交线:y=0 => x+z=1
x_line3 = t;
z_line3 = 1 - x_line3;
plot3(x_line3, zeros(size(t)), z_line3, 'b-', 'LineWidth', 2);
% 设置视角
view(45, 30);
% 添加图例
legend({'平面 x+y+z=1', 'x轴交点(1,0,0)', 'y轴交点(0,1,0)', 'z轴交点(0,0,1)', ...
'与xy平面交线', '与yz平面交线', '与xz平面交线'}, ...
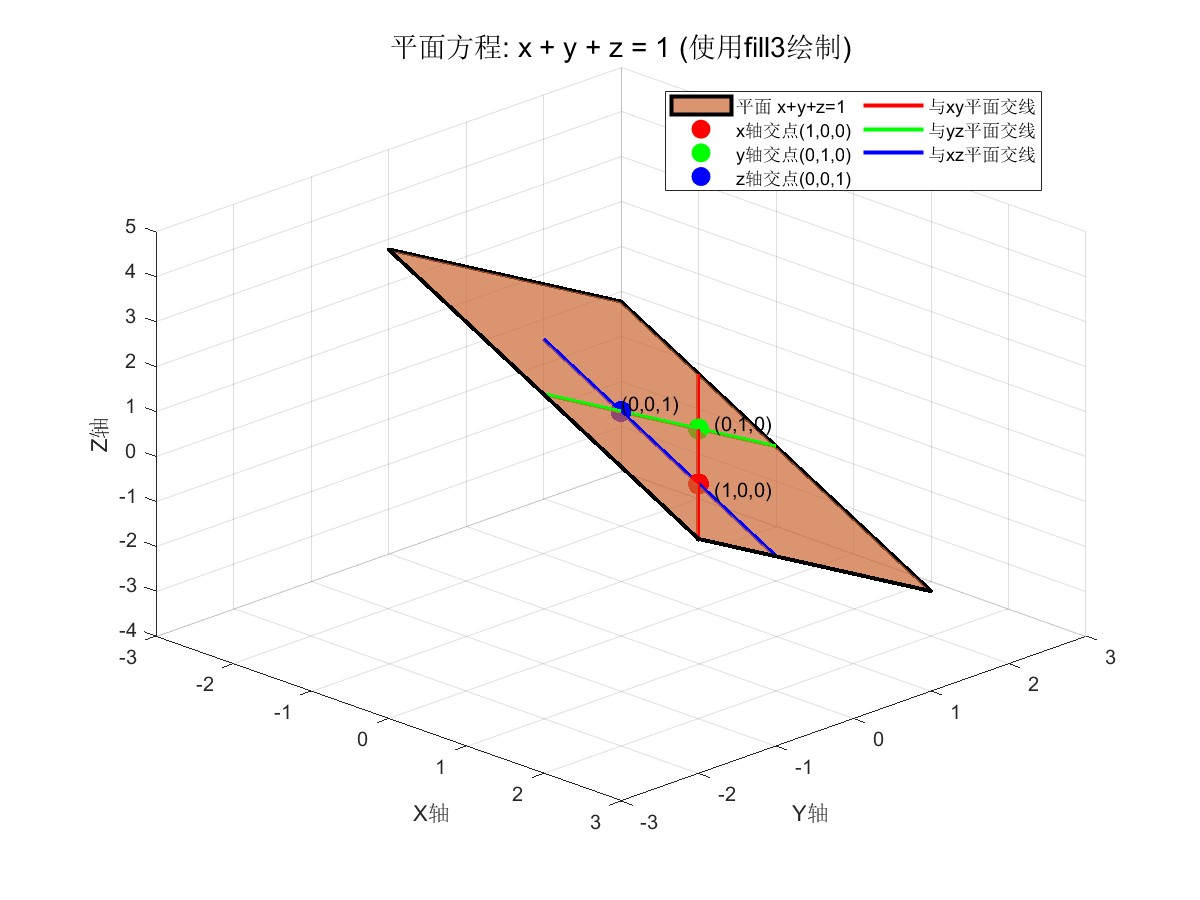
'Location', 'best', 'NumColumns', 2);这段MATLAB代码演示了如何利用三维可视化工具,将抽象的平面方程𝑥+𝑦+𝑧=1转化为一个直观、可交互的图形。代码首先定义了一个由四个特定顶点构成的四边形,该四边形是平面在三维空间中的一个有限区域,并通过 fill3 函数以半透明的橙黄色进行填充,同时勾勒出清晰的黑色边界。
为了帮助读者理解该平面在空间中的几何特性,代码精心绘制了三个关键元素:
一是用红、绿、蓝色实心圆点明确标出了平面与三个坐标轴的交点(即截距点);
二是用三种不同颜色的实线分别绘制了该平面与三个坐标平面(XY、YZ、XZ平面)的交线;
这些元素共同清晰地揭示了平面方程𝑥+𝑦+𝑧=1的几何意义。
整个可视化过程还包含了完整的坐标轴设置、网格、图例和特定的三维视角,最终生成了下面的图形。
3.x+y+z=0与x+y+z=1的区别
Matlab
%% 在同一图中绘制两个平面 x+y+z=0 和 x+y+z=1
figure('Position', [100, 100, 1000, 800]);
% ==================== 绘制平面 x+y+z=0 ====================
% 定义平面 x+y+z=0 的四个角点
vertices0 = [
-4, -4, 8; % 点1: (-4,-4,8) 因为 -4-4+8=0
4, -4, 0; % 点2: (4,-4,0) 因为 4-4+0=0
4, 4, -8; % 点3: (4,4,-8) 因为 4+4-8=0
-4, 4, 0; % 点4: (-4,4,0) 因为 -4+4+0=0
];
% 使用 fill3 绘制平面 x+y+z=0
fill3(vertices0(:,1), vertices0(:,2), vertices0(:,3), [0.2, 0.6, 0.8], ...
'FaceAlpha', 0.6, 'EdgeColor', 'b', 'LineWidth', 1.5, 'LineStyle', '-');
hold on;
% ==================== 绘制平面 x+y+z=1 ====================
% 定义平面 x+y+z=1 的四个角点
vertices1 = [
3, -2, 0; % 点1: (3,-2,0) 因为 3-2+0=1
3, 3, -5; % 点2: (3,3,-5) 因为 3+3-5=1
-3, 3, 1; % 点3: (-3,3,1) 因为 -3+3+1=1
-3, -2, 6; % 点4: (-3,-2,6) 因为 -3-2+6=1
];
% 使用 fill3 绘制平面 x+y+z=1
fill3(vertices1(:,1), vertices1(:,2), vertices1(:,3), [0.8, 0.4, 0.2], ...
'FaceAlpha', 0.6, 'EdgeColor', 'r', 'LineWidth', 1.5, 'LineStyle', '--');
% ==================== 设置坐标系和标签 ====================
% 设置坐标轴范围
xlim([-6, 6]); ylim([-6, 6]); zlim([-10, 10]);
% 添加坐标轴标签
xlabel('X轴', 'FontSize', 12, 'FontWeight', 'bold');
ylabel('Y轴', 'FontSize', 12, 'FontWeight', 'bold');
zlabel('Z轴', 'FontSize', 12, 'FontWeight', 'bold');
% 添加标题
title('两个平行平面的比较: x+y+z=0 和 x+y+z=1', 'FontSize', 14, 'FontWeight', 'bold');
grid on;
box on;
% ==================== 添加关键点和特征线 ====================
% 原点 (平面 x+y+z=0 上)
plot3(0, 0, 0, 'ko', 'MarkerSize', 10, 'MarkerFaceColor', 'k');
text(0.5, 0.5, 0.5, '原点(0,0,0)', 'FontSize', 10);
% 平面 x+y+z=1 与坐标轴的交点
plot3(1, 0, 0, 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
plot3(0, 1, 0, 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g');
plot3(0, 0, 1, 'bo', 'MarkerSize', 10, 'MarkerFaceColor', 'b');
text(1.2, 0, 0, '(1,0,0)', 'FontSize', 10);
text(0, 1.2, 0, '(0,1,0)', 'FontSize', 10);
text(0, 0, 1.2, '(0,0,1)', 'FontSize', 10);
% 两个平面的法向量 (相同)
% 从原点画法向量
quiver3(0, 0, 0, 2, 2, 2, 'LineWidth', 2, 'Color', 'm', 'MaxHeadSize', 0.5);
% 从平面 x+y+z=1 上的一点画法向量
quiver3(1/3, 1/3, 1/3, 2, 2, 2, 'LineWidth', 2, 'Color', 'm', 'MaxHeadSize', 0.5);
text(2.5, 2.5, 2.5, '法向量 (1,1,1)', 'FontSize', 11, 'Color', 'm');
% ==================== 添加两个平面上的特征线 ====================
t = linspace(-4, 4, 50);
% 平面 x+y+z=0 上的线
% 当 y=0 时,z = -x
line0_y0_x = t;
line0_y0_y = zeros(size(t));
line0_y0_z = -t;
plot3(line0_y0_x, line0_y0_y, line0_y0_z, 'b-', 'LineWidth', 1.5);
% 当 x=0 时,z = -y
line0_x0_x = zeros(size(t));
line0_x0_y = t;
line0_x0_z = -t;
plot3(line0_x0_x, line0_x0_y, line0_x0_z, 'b-', 'LineWidth', 1.5);
% 平面 x+y+z=1 上的线
% 与 xy 平面的交线 (z=0)
line1_z0_t = linspace(-2, 3, 50);
line1_z0_x = line1_z0_t;
line1_z0_y = 1 - line1_z0_t;
line1_z0_z = zeros(size(line1_z0_t));
plot3(line1_z0_x, line1_z0_y, line1_z0_z, 'r-', 'LineWidth', 1.5);
% 与 xz 平面的交线 (y=0)
line1_y0_t = linspace(-2, 3, 50);
line1_y0_x = line1_y0_t;
line1_y0_y = zeros(size(line1_y0_t));
line1_y0_z = 1 - line1_y0_t;
plot3(line1_y0_x, line1_y0_y, line1_y0_z, 'r-', 'LineWidth', 1.5);
% ==================== 添加连接两个平面的垂线 ====================
% 计算两个平面的距离
plane_distance = 1 / sqrt(3); % |1-0| / √(1²+1²+1²) = 1/√3 ≈ 0.577
% 在原点处画垂线到平面 x+y+z=1
% 原点在平面 x+y+z=0 上
% 从原点到平面 x+y+z=1 的垂足是 (1/3, 1/3, 1/3)
plot3([0, 1/3], [0, 1/3], [0, 1/3], 'k--', 'LineWidth', 2);
text(0.2, 0.2, 0.2, sprintf('距离=%.3f', plane_distance), 'FontSize', 10);
% ==================== 添加图例和文本说明 ====================
legend_entries = {
'平面 x+y+z=0 (通过原点)', ...
'平面 x+y+z=1 (常数项为1)', ...
'原点 (0,0,0)', ...
'平面交点 (1,0,0)', ...
'平面交点 (0,1,0)', ...
'平面交点 (0,0,1)', ...
'法向量 (1,1,1)', ...
'平面 x+y+z=0 上的线', ...
'平面 x+y+z=1 上的线', ...
'两平面间的垂线'
};
% 创建图例(只包含主要元素)
legend({'平面 x+y+z=0', '平面 x+y+z=1', '原点', ...
'x轴交点', 'y轴交点', 'z轴交点', ...
'法向量', '平面0上的线', '平面1上的线', '垂线'}, ...
'Location', 'best', 'NumColumns', 2);
% 添加文本说明
text(-5.5, -5.5, 8, '两个平面平行', 'FontSize', 11, 'BackgroundColor', 'w');
text(-5.5, -5.5, 7, '法向量相同: (1,1,1)', 'FontSize', 11, 'BackgroundColor', 'w');
text(-5.5, -5.5, 6, sprintf('距离: 1/√3 ≈ %.3f', plane_distance), 'FontSize', 11, 'BackgroundColor', 'w');
% ==================== 设置视角和美化图形 ====================
% 设置视角
view(45, 25);
% 添加光照效果
light('Position', [1, 1, 1]);
lighting gouraud;
% 添加颜色条说明
colormap([0.2, 0.6, 0.8; 0.8, 0.4, 0.2]);
% 手动添加颜色条说明
annotation('textbox', [0.02, 0.9, 0.2, 0.05], 'String', '蓝色: x+y+z=0', ...
'Color', [0.2, 0.6, 0.8], 'FontWeight', 'bold', 'EdgeColor', 'none', 'BackgroundColor', 'w');
annotation('textbox', [0.02, 0.85, 0.2, 0.05], 'String', '橙色: x+y+z=1', ...
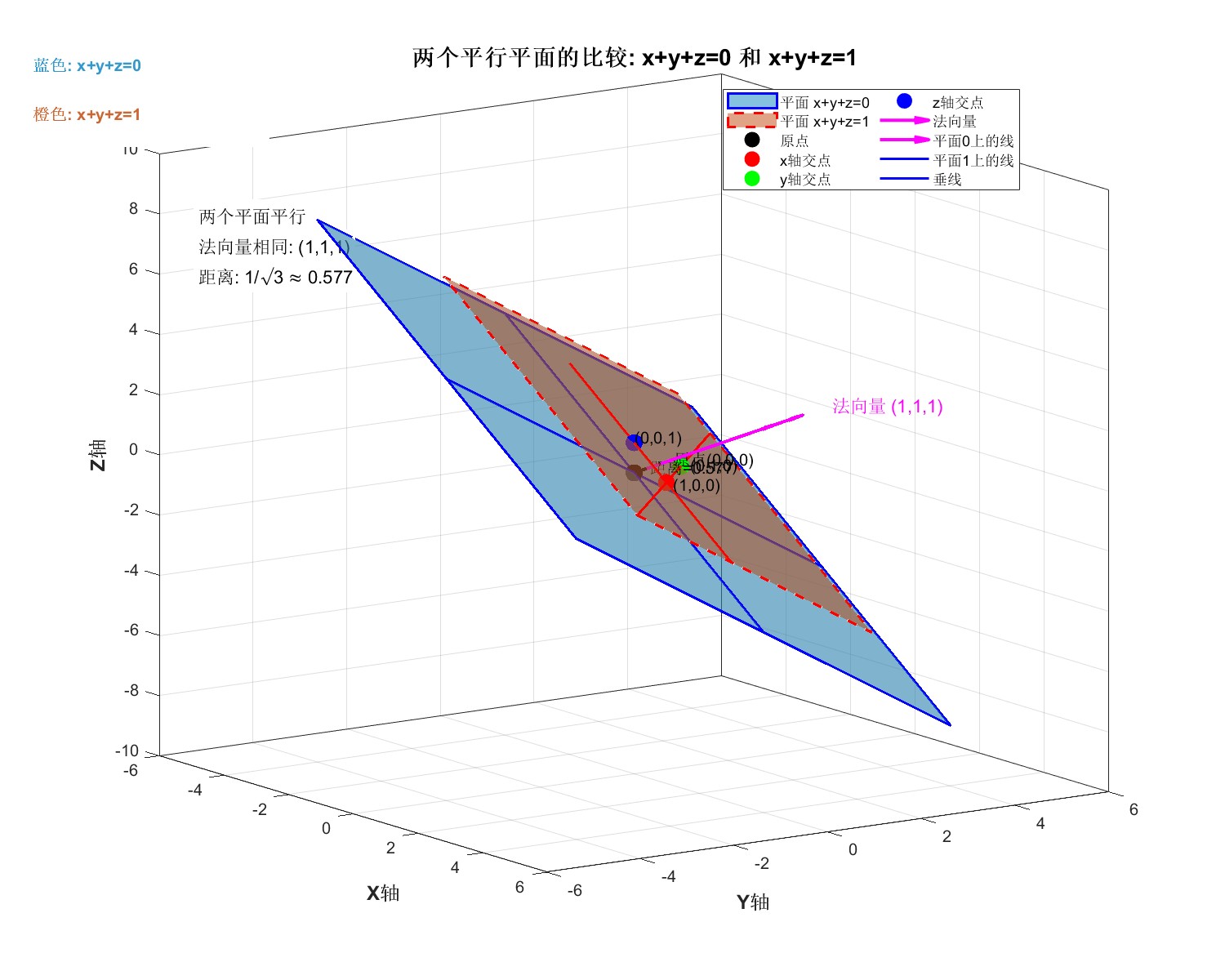
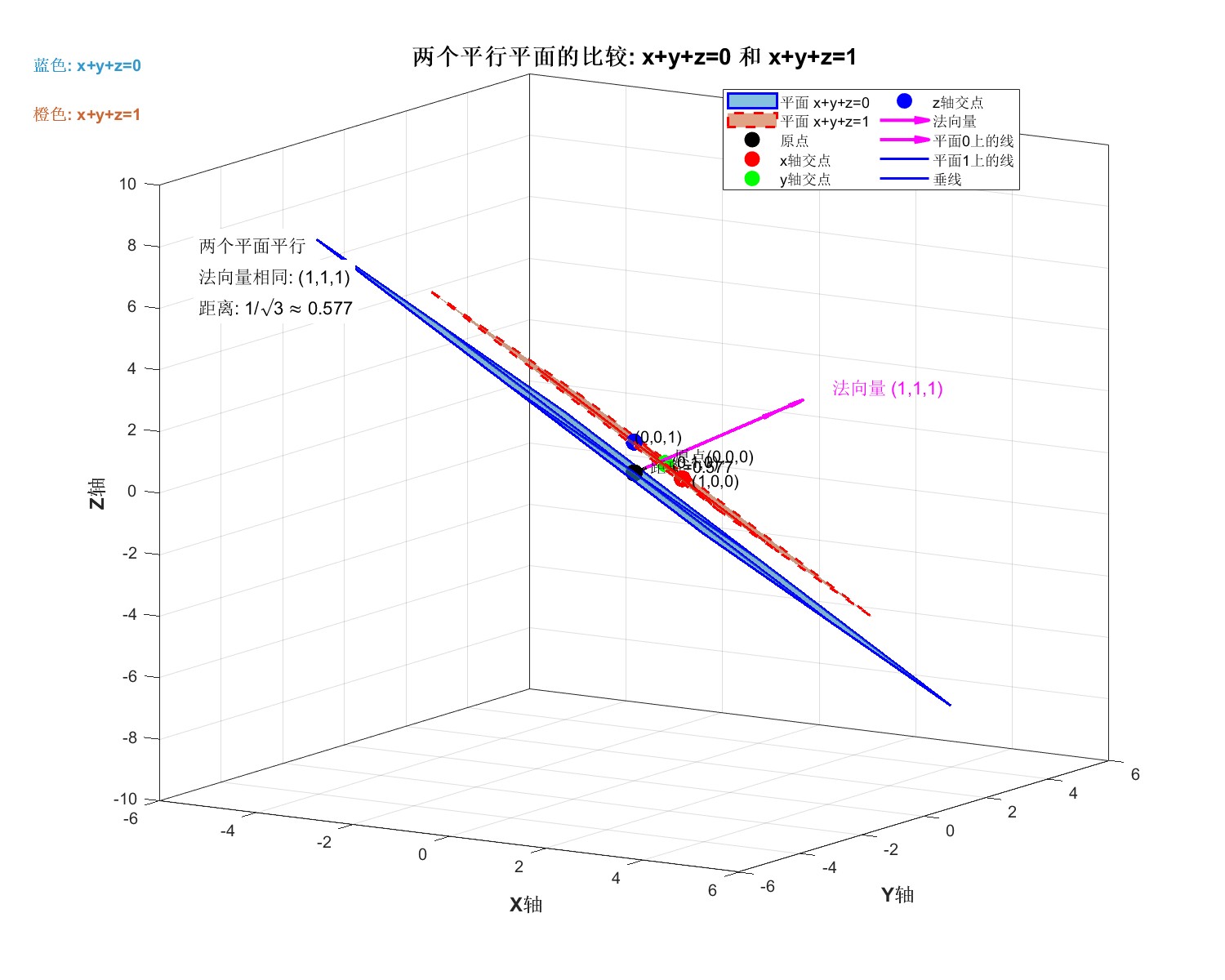
'Color', [0.8, 0.4, 0.2], 'FontWeight', 'bold', 'EdgeColor', 'none', 'BackgroundColor', 'w');这段MATLAB代码创建了一个综合性的三维可视化图形,旨在展示两个平行平面 𝑥+𝑦+𝑧=0和𝑥+𝑦+𝑧=1在空间中的几何关系。代码使用半透明的四边形分别代表这两个平面:蓝色的𝑥+𝑦+𝑧=0平面采用实线边框,橙色的𝑥+𝑦+𝑧=1平面则使用虚线边框。为了清晰地表明两平面的平行特性,代码从两个不同点出发绘制了相同的品红色法向量(1,1,1),并计算标注了它们之间的精确距离。
为了深化几何理解,代码标注了多个关键特征点,包括原点(位于第一个平面上)、第二个平面与各坐标轴的交点,并在两个平面上绘制了代表性的交线(如与坐标平面的交线)。一个关键细节是绘制了从原点到第二个平面的垂线,直观地展示了"距离"的定义。图形还设置了完整的坐标轴、网格、光照效果和特定的观察视角,以增强三维感知。
最终生成的图形不仅清晰地展示了两平面的平行关系,还通过丰富的注释、图例和文本框,全面解释了它们的法向量、距离公式及空间位置关系,形成一个信息完整、极具教学价值的可视化示例,非常适合用于几何或线性代数的教学演示。
4.介于平面x+y+z=0与平面x+y+z=1之间部分的外侧
Matlab
%% 绘制介于平面 x+y+z=0 与 x+y+z=1 之间的外侧部分
figure('Position', [100, 100, 1200, 800]);
% ==================== 定义参数 ====================
% 定义网格大小和范围
x_range = -4:0.5:4;
y_range = -4:0.5:4;
[x, y] = meshgrid(x_range, y_range);
% ==================== 绘制两个平面 ====================
% 平面1: x+y+z=0
z1 = -x - y;
% 平面2: x+y+z=1
z2 = 1 - x - y;
% 绘制平面1 (透明,作为参考)
surf(x, y, z1, 'FaceColor', [0.2, 0.6, 0.8], 'FaceAlpha', 0.2, 'EdgeColor', 'none');
hold on;
% 绘制平面2 (透明,作为参考)
surf(x, y, z2, 'FaceColor', [0.8, 0.4, 0.2], 'FaceAlpha', 0.2, 'EdgeColor', 'none');
% ==================== 绘制两个平面之间的外侧区域 ====================
% 我们创建一个封闭的体,表示两个平面之间的区域
% 首先定义边界框
x_min = min(x_range); x_max = max(x_range);
y_min = min(y_range); y_max = max(y_range);
% 创建一个网格,用于在两个平面之间填充
[x_fill, y_fill] = meshgrid(linspace(x_min, x_max, 20), linspace(y_min, y_max, 20));
z_fill1 = -x_fill - y_fill; % 平面1
z_fill2 = 1 - x_fill - y_fill; % 平面2
% 绘制两个平面之间的体 (使用多个面)
% 绘制侧面的四个面
% 1. 右侧面 (x = x_max)
x_right = x_max * ones(size(y_fill));
z_right1 = -x_right - y_fill;
z_right2 = 1 - x_right - y_fill;
surf(x_right, y_fill, z_right1, z_right2, ...
'FaceColor', [0.5, 0.5, 0.7], 'FaceAlpha', 0.7, 'EdgeColor', 'none');
% 2. 左侧面 (x = x_min)
x_left = x_min * ones(size(y_fill));
z_left1 = -x_left - y_fill;
z_left2 = 1 - x_left - y_fill;
surf(x_left, y_fill, z_left1, z_left2, ...
'FaceColor', [0.5, 0.5, 0.7], 'FaceAlpha', 0.7, 'EdgeColor', 'none');
% 3. 前面 (y = y_max)
y_front = y_max * ones(size(x_fill));
z_front1 = -x_fill - y_front;
z_front2 = 1 - x_fill - y_front;
surf(x_fill, y_front, z_front1, z_front2, ...
'FaceColor', [0.5, 0.7, 0.5], 'FaceAlpha', 0.7, 'EdgeColor', 'none');
% 4. 后面 (y = y_min)
y_back = y_min * ones(size(x_fill));
z_back1 = -x_fill - y_back;
z_back2 = 1 - x_fill - y_back;
surf(x_fill, y_back, z_back1, z_back2, ...
'FaceColor', [0.5, 0.7, 0.5], 'FaceAlpha', 0.7, 'EdgeColor', 'none');
% 绘制上下两个平面 (使用更透明的效果)
% 下平面 (平面1)
surf(x_fill, y_fill, z_fill1, ...
'FaceColor', [0.2, 0.6, 0.8], 'FaceAlpha', 0.3, 'EdgeColor', 'none');
% 上平面 (平面2)
surf(x_fill, y_fill, z_fill2, ...
'FaceColor', [0.8, 0.4, 0.2], 'FaceAlpha', 0.3, 'EdgeColor', 'none');
% ==================== 绘制外侧边缘 ====================
% 绘制两个平面之间区域的边界线
% 计算四个边角点
corners = [
x_min, y_min, -x_min-y_min; % 平面1上的点
x_max, y_min, -x_max-y_min;
x_max, y_max, -x_max-y_max;
x_min, y_max, -x_min-y_max;
x_min, y_min, 1-x_min-y_min; % 平面2上的点
x_max, y_min, 1-x_max-y_min;
x_max, y_max, 1-x_max-y_max;
x_min, y_max, 1-x_min-y_max;
];
% 绘制边界线
% 底部矩形的边
bottom_edges = [1,2; 2,3; 3,4; 4,1];
for i = 1:size(bottom_edges, 1)
idx = bottom_edges(i, :);
plot3(corners(idx, 1), corners(idx, 2), corners(idx, 3), ...
'b-', 'LineWidth', 2.5);
end
% 顶部矩形的边
top_edges = [5,6; 6,7; 7,8; 8,5];
for i = 1:size(top_edges, 1)
idx = top_edges(i, :);
plot3(corners(idx, 1), corners(idx, 2), corners(idx, 3), ...
'r-', 'LineWidth', 2.5);
end
% 连接上下平面的垂直线
vertical_edges = [1,5; 2,6; 3,7; 4,8];
for i = 1:size(vertical_edges, 1)
idx = vertical_edges(i, :);
plot3(corners(idx, 1), corners(idx, 2), corners(idx, 3), ...
'k-', 'LineWidth', 2, 'LineStyle', '--');
end
% ==================== 添加关键点和注释 ====================
% 原点
plot3(0, 0, 0, 'ko', 'MarkerSize', 12, 'MarkerFaceColor', 'k');
text(0.5, 0.5, 0.5, '原点(0,0,0)', 'FontSize', 11, 'FontWeight', 'bold');
% 平面 x+y+z=1 与坐标轴的交点
plot3(1, 0, 0, 'ro', 'MarkerSize', 12, 'MarkerFaceColor', 'r');
plot3(0, 1, 0, 'go', 'MarkerSize', 12, 'MarkerFaceColor', 'g');
plot3(0, 0, 1, 'bo', 'MarkerSize', 12, 'MarkerFaceColor', 'b');
text(1.2, 0, 0, '(1,0,0)', 'FontSize', 11, 'FontWeight', 'bold');
text(0, 1.2, 0, '(0,1,0)', 'FontSize', 11, 'FontWeight', 'bold');
text(0, 0, 1.2, '(0,0,1)', 'FontSize', 11, 'FontWeight', 'bold');
% 法向量
quiver3(0, 0, 0, 2, 2, 2, 'LineWidth', 3, 'Color', 'm', 'MaxHeadSize', 0.5);
quiver3(0.5, 0.5, 0.5, 2, 2, 2, 'LineWidth', 3, 'Color', 'm', 'MaxHeadSize', 0.5, 'LineStyle', ':');
text(2.5, 2.5, 2.5, '法向量 (1,1,1)', 'FontSize', 12, 'Color', 'm', 'FontWeight', 'bold');
% ==================== 计算并显示体积 ====================
% 两个平面之间的距离
plane_distance = 1 / sqrt(3);
% 区域的底面积 (在xy平面上的投影)
area = (x_max - x_min) * (y_max - y_min);
% 体积近似值
volume_approx = area * plane_distance;
% 添加体积信息
text(-3.5, -3.5, 8, sprintf('平面间距离: %.3f', plane_distance), ...
'FontSize', 11, 'BackgroundColor', 'w', 'FontWeight', 'bold');
text(-3.5, -3.5, 7, sprintf('区域体积: ≈ %.3f', volume_approx), ...
'FontSize', 11, 'BackgroundColor', 'w', 'FontWeight', 'bold');
% ==================== 设置坐标系和标签 ====================
% 设置坐标轴范围
xlim([x_min-0.5, x_max+0.5]);
ylim([y_min-0.5, y_max+0.5]);
zlim([min([z1(:); z2(:)])-1, max([z1(:); z2(:)])+1]);
% 添加坐标轴标签
xlabel('X轴', 'FontSize', 13, 'FontWeight', 'bold');
ylabel('Y轴', 'FontSize', 13, 'FontWeight', 'bold');
zlabel('Z轴', 'FontSize', 13, 'FontWeight', 'bold');
% 添加标题
title('介于平面 x+y+z=0 与 x+y+z=1 之间的外侧区域', ...
'FontSize', 16, 'FontWeight', 'bold');
grid on;
% ==================== 添加图例 ====================
legend_entries = {
'平面 x+y+z=0 (透明)', ...
'平面 x+y+z=1 (透明)', ...
'侧面 (x=±4)', ...
'侧面 (y=±4)', ...
'下平面 (x+y+z=0)', ...
'上平面 (x+y+z=1)', ...
'下边界', ...
'上边界', ...
'垂直线', ...
'原点', ...
'上平面与坐标轴交点', ...
'法向量'
};
% 简化图例
legend({'平面 x+y+z=0', '平面 x+y+z=1', '侧面区域', ...
'下平面边界', '上平面边界', '垂直线', ...
'原点', '平面交点', '法向量'}, ...
'Location', 'best', 'NumColumns', 2, 'FontSize', 10);
% ==================== 设置视角和美化 ====================
% 设置视角
view(45, 25);
% 添加光照效果
light('Position', [1, 1, 1], 'Style', 'infinite');
light('Position', [-1, -1, 1], 'Style', 'infinite');
lighting gouraud;
% 添加颜色说明
annotation('textbox', [0.02, 0.95, 0.2, 0.04], 'String', '蓝色: x+y+z=0', ...
'Color', [0.2, 0.6, 0.8], 'FontWeight', 'bold', 'EdgeColor', 'none', ...
'BackgroundColor', 'w', 'FontSize', 11);
annotation('textbox', [0.02, 0.90, 0.2, 0.04], 'String', '橙色: x+y+z=1', ...
'Color', [0.8, 0.4, 0.2], 'FontWeight', 'bold', 'EdgeColor', 'none', ...
'BackgroundColor', 'w', 'FontSize', 11);
annotation('textbox', [0.02, 0.85, 0.2, 0.04], 'String', '灰色: 侧面区域', ...
'Color', [0.5, 0.5, 0.7], 'FontWeight', 'bold', 'EdgeColor', 'none', ...
'BackgroundColor', 'w', 'FontSize', 11);
% 添加交互式旋转提示
annotation('textbox', [0.7, 0.02, 0.25, 0.04], 'String', '提示: 使用工具栏旋转按钮查看三维效果', ...
'Color', 'k', 'FontWeight', 'bold', 'EdgeColor', 'none', ...
'BackgroundColor', [0.9, 0.9, 0.9], 'FontSize', 10);
% 设置背景颜色
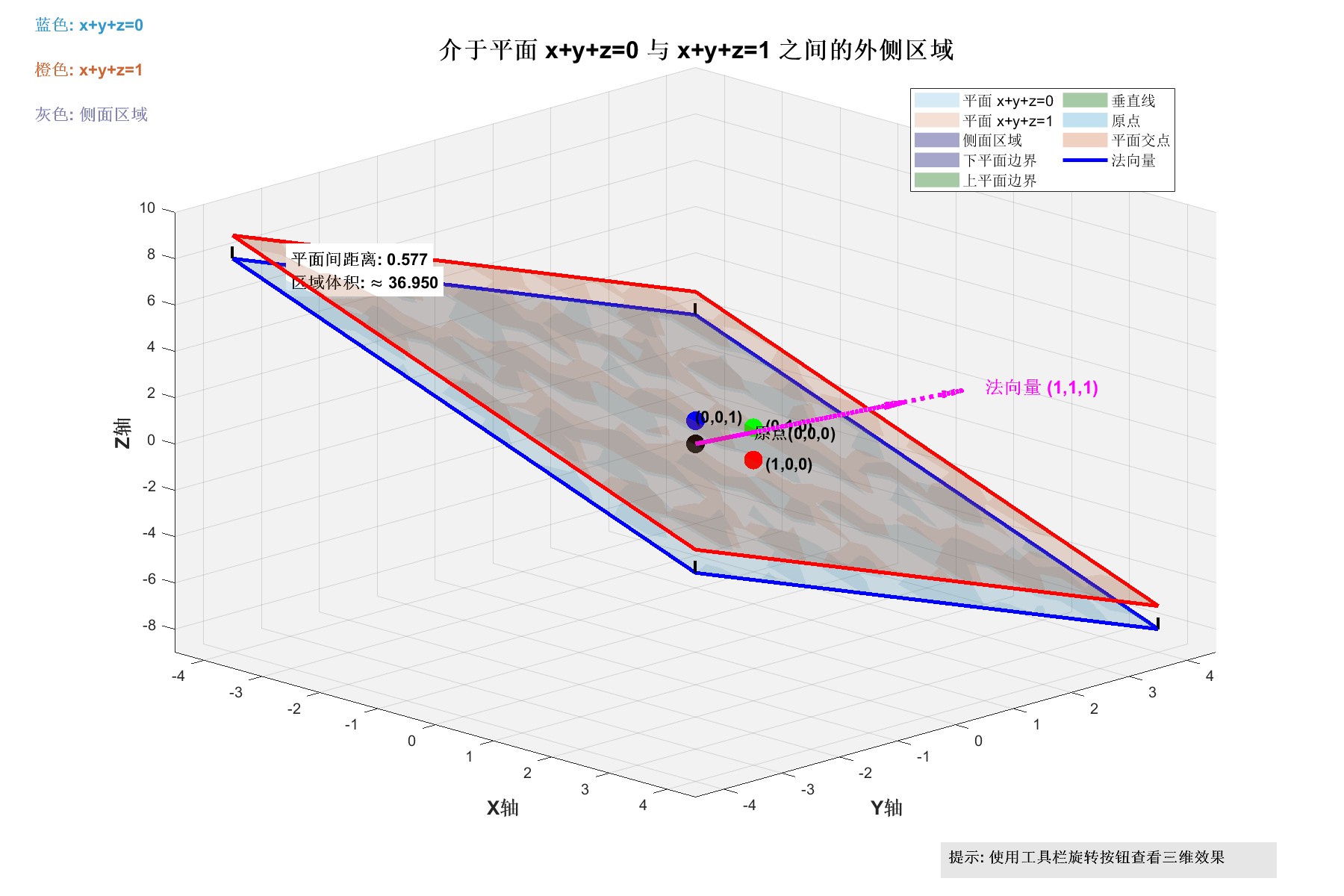
set(gca, 'Color', [0.95, 0.95, 0.95]);这段MATLAB代码创建了一个高级三维可视化,重点展示平行平面𝑥+𝑦+𝑧=0和𝑥+𝑦+𝑧=1之间限定区域的三维立体结构。代码首先生成两个平面的透明网格作为背景参考,然后巧妙构建了一个由六个面组成的封闭立体区域:除了上下两个原始平面(分别用半透明蓝橙两色表示),还添加了四个侧面(采用不同灰度的填充色),形成一个完整的平行六面体结构。为了清晰界定这一立体区域,代码绘制了区分上下边界的实线边框和连接两个平面的垂直虚线,并标注了八个角点,使空间结构一目了然。
图形中嵌入了丰富的几何信息与计算指标,不仅标注了原点、平面与坐标轴的交点,还绘制了两个平面的共同法向量以强调其平行关系。更有特色的是,代码通过计算两个平面间的距离 (1/31/3) 和该立体区域在有限坐标范围内的投影底面积,近似估算出了区域的体积并直接显示在图形上,将抽象概念转化为具体数值。这使得可视化不仅是空间关系的展示,更成为了一个验证几何计算的教学工具。
最终的可视化结果经过全面优化,包括设置恰当的三维视角、添加多重光照效果、使用醒目的图例和文本框进行颜色编码说明,甚至加入了交互式旋转的提示。背景色调、字体加粗等细节处理增强了整体的可读性和美观度,创造出一个兼具教学深度与视觉吸引力的三维图形,非常适合用于演示空间中平面所界定的区域及其几何属性。
5.直线1{x=0,y=0}
Matlab
% 设置 z 轴的范围
z = linspace(-10, 10, 100);
% 由于直线是 z 轴,x 和 y 始终为 0
x = zeros(size(z));
y = zeros(size(z));
% 创建图形窗口
figure;
% 绘制直线
plot3(x, y, z, 'b-', 'LineWidth', 2);
hold on;
% 标记原点
plot3(0, 0, 0, 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
% 设置图形属性
xlabel('X轴');
ylabel('Y轴');
zlabel('Z轴');
title('直线: x=0, y=0 (z轴)');
grid on;
axis equal;
xlim([-1 1]);
ylim([-1 1]);
zlim([-10 10]);
% 添加图例
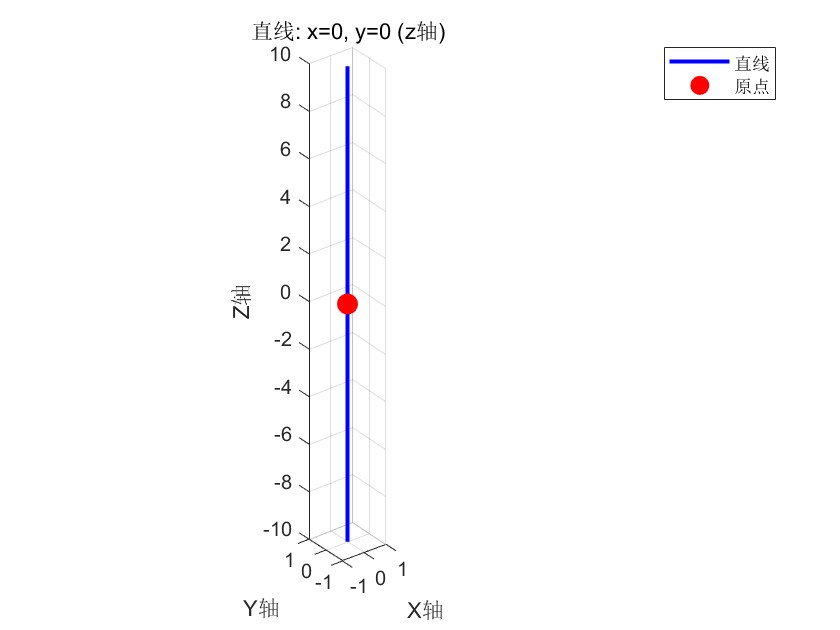
legend('直线', '原点');该MATLAB代码绘制了三维空间中的z轴直线。它定义了一条由点(0,0,z)组成的直线,其中z坐标在-10到10范围内均匀分布。
代码使用蓝色实线绘制这条直线,并在原点(0,0,0)处标记一个红色实心圆点。图形设置了坐标轴标签、标题和网格线,确保x和y轴显示范围在-1到1之间,z轴范围在-10到10之间,并采用等比例缩放以保持视觉准确性。
最后添加图例区分直线和原点标记,形成一个清晰展示三维坐标轴中z轴位置的空间直线可视化图形。
6.直线2{x=t,y=t,z=t}
Matlab
%% 绘制直线2:{x=t, y=t, z=t}
figure(2); % 创建第二个图形窗口
% 设置参数t的范围
t = linspace(-10, 10, 100);
% 计算x, y, z坐标
x2 = t;
y2 = t;
z2 = t;
% 绘制直线
plot3(x2, y2, z2, 'r-', 'LineWidth', 2);
hold on;
% 标记原点
plot3(0, 0, 0, 'bo', 'MarkerSize', 10, 'MarkerFaceColor', 'b');
% 设置图形属性
xlabel('X轴');
ylabel('Y轴');
zlabel('Z轴');
title('直线2: x=t, y=t, z=t');
grid on;
axis equal;
xlim([-10 10]);
ylim([-10 10]);
zlim([-10 10]);
% 添加图例
legend('直线', '原点', 'Location', 'best');
% 添加参考平面
[X, Y] = meshgrid(-10:2:10, -10:2:10);
Z = zeros(size(X));
mesh(X, Y, Z, 'FaceAlpha', 0.2, 'EdgeColor', 'k', 'FaceColor', 'none');
% 添加坐标平面指示线
plot3([-10, 10], [0, 0], [0, 0], 'k--', 'LineWidth', 0.5); % x轴
plot3([0, 0], [-10, 10], [0, 0], 'k--', 'LineWidth', 0.5); % y轴
plot3([0, 0], [0, 0], [-10, 10], 'k--', 'LineWidth', 0.5); % z轴
% 添加标签
text(10, 0, 0, 'X', 'FontSize', 12);
text(0, 10, 0, 'Y', 'FontSize', 12);
text(0, 0, 10, 'Z', 'FontSize', 12);
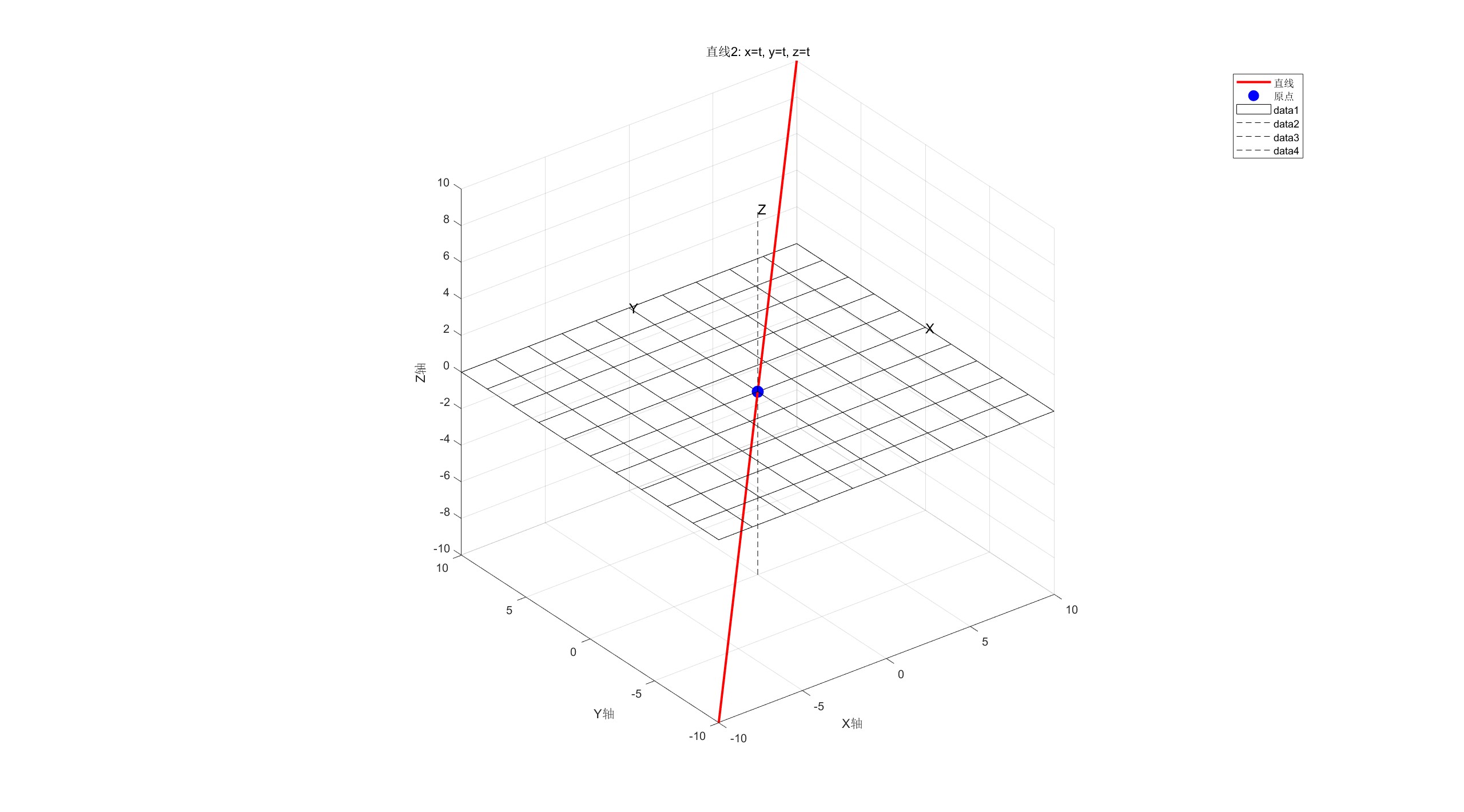
hold off;这段MATLAB代码绘制了三维空间中的一条参数直线,其方程为x=t,y=t,z=t。
代码创建了一个新的图形窗口,使用红色实线绘制了当参数t在[−10,10] 范围内变化时直线的轨迹,并在原点标记了一个蓝色实心点。
为了增强空间参照,代码添加了一个半透明的网格平面(代表z=0 平面)和三条虚线坐标轴,并标注了X、Y、Z字母标签。
图形设置了坐标轴标签、标题、网格、等比例缩放以及统一的坐标范围,最后添加图例以区分直线和原点。整体上,该可视化清晰展示了这条通过原点且与三个坐标轴夹角相等的空间直线。
7.直线1{x=0,y=0}绕直线2{x=t,y=t,z=t}旋转得到的曲面
Matlab
%% 绘制旋转曲面:直线1绕直线2旋转
figure('Position', [100, 100, 1200, 500]);
%% 子图1:显示两条直线和旋转示意图
subplot(1, 2, 1);
hold on;
grid on;
axis equal;
% 绘制直线1(z轴)
z1 = linspace(-5, 5, 100);
x1 = zeros(size(z1));
y1 = zeros(size(z1));
plot3(x1, y1, z1, 'b-', 'LineWidth', 3);
% 绘制直线2(对角线)
t = linspace(-5, 5, 100);
x2 = t;
y2 = t;
z2 = t;
plot3(x2, y2, z2, 'r-', 'LineWidth', 3);
% 绘制旋转示意图
% 绕直线2旋转直线1的多个位置
theta = linspace(0, 2*pi, 12); % 12个旋转角度
for i = 1:length(theta)
% 对直线1上的点应用旋转矩阵
% 旋转轴:直线2的方向向量 [1, 1, 1]
% 旋转角度:theta(i)
% 创建旋转矩阵(绕任意轴旋转)
axis_vec = [1, 1, 1]; % 旋转轴方向向量
axis_vec = axis_vec / norm(axis_vec); % 单位化
% 旋转矩阵(使用Rodrigues旋转公式)
theta_i = theta(i);
K = [0, -axis_vec(3), axis_vec(2);
axis_vec(3), 0, -axis_vec(1);
-axis_vec(2), axis_vec(1), 0];
R = eye(3) + sin(theta_i) * K + (1 - cos(theta_i)) * (K * K);
% 对直线1上的点应用旋转
for j = 1:length(z1)
point = [x1(j); y1(j); z1(j)];
rotated_point = R * point;
if j == 1
plot3(rotated_point(1), rotated_point(2), rotated_point(3), 'g-', 'LineWidth', 1);
else
plot3(rotated_point(1), rotated_point(2), rotated_point(3), 'g-', 'LineWidth', 1);
end
end
end
% 设置图形属性
xlabel('X轴');
ylabel('Y轴');
zlabel('Z轴');
title('旋转示意图');
legend('直线1 (z轴)', '直线2 (旋转轴)', '旋转中的直线1位置');
view(45, 30); % 设置视角
%% 子图2:绘制完整的旋转曲面
subplot(1, 2, 2);
hold on;
grid on;
axis equal;
% 创建网格参数
u = linspace(0, 2*pi, 50); % 旋转角度
v = linspace(-5, 5, 50); % 直线1上的z坐标
[U, V] = meshgrid(u, v);
% 初始化曲面坐标矩阵
X = zeros(size(U));
Y = zeros(size(U));
Z = zeros(size(U));
% 直线2的方向向量(旋转轴)
axis_vec = [1, 1, 1];
axis_vec = axis_vec / norm(axis_vec);
% 对每个网格点计算旋转后的坐标
for i = 1:size(U, 1)
for j = 1:size(U, 2)
% 直线1上的原始点
original_point = [0; 0; V(i, j)];
% 旋转角度
theta = U(i, j);
% Rodrigues旋转公式
K = [0, -axis_vec(3), axis_vec(2);
axis_vec(3), 0, -axis_vec(1);
-axis_vec(2), axis_vec(1), 0];
R = eye(3) + sin(theta) * K + (1 - cos(theta)) * (K * K);
% 计算旋转后的点
rotated_point = R * original_point;
% 存储坐标
X(i, j) = rotated_point(1);
Y(i, j) = rotated_point(2);
Z(i, j) = rotated_point(3);
end
end
% 绘制曲面
surf(X, Y, Z, 'FaceColor', 'cyan', 'EdgeColor', 'none', 'FaceAlpha', 0.7);
% 在曲面上添加一些特征线
% 绘制原始直线1
plot3(x1, y1, z1, 'b-', 'LineWidth', 3);
% 绘制旋转轴(直线2)
plot3(x2, y2, z2, 'r-', 'LineWidth', 3);
% 添加一些旋转轮廓线
num_profiles = 8;
for i = 1:num_profiles
idx = round(size(U, 2) * i / num_profiles);
if idx > size(U, 2)
idx = size(U, 2);
end
plot3(X(:, idx), Y(:, idx), Z(:, idx), 'k-', 'LineWidth', 1);
end
% 设置图形属性
xlabel('X轴');
ylabel('Y轴');
zlabel('Z轴');
title('旋转曲面:直线1绕直线2旋转');
view(45, 30); % 设置视角
lighting gouraud;
light('Position', [1, 1, 1]);
% 添加颜色条显示高度
c = colorbar;
c.Label.String = 'Z坐标';
% 添加注释
text(0, 0, 6, '旋转曲面', 'FontSize', 12, 'FontWeight', 'bold', 'HorizontalAlignment', 'center');
text(3, 3, 5, '旋转轴', 'FontSize', 10, 'Color', 'r');
% 调整图形
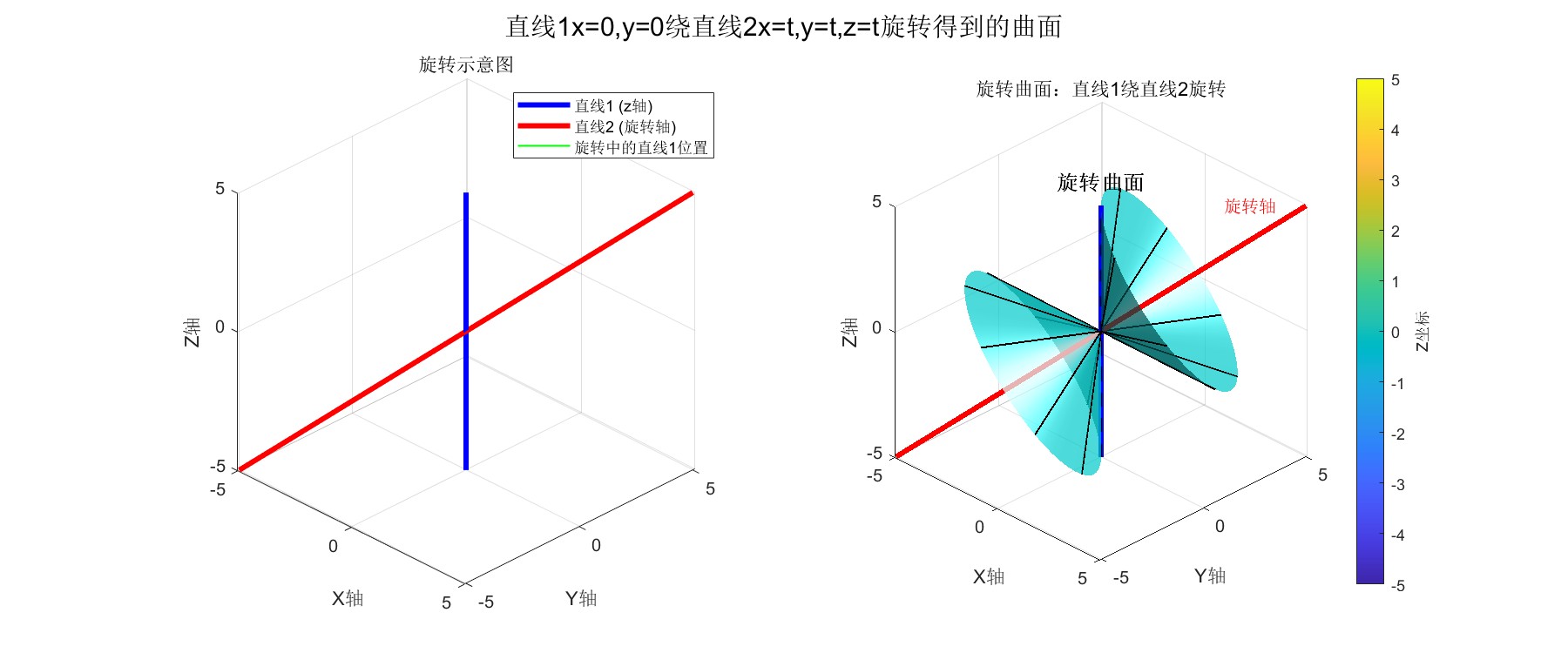
sgtitle('直线1{x=0,y=0}绕直线2{x=t,y=t,z=t}旋转得到的曲面');这段MATLAB代码通过两个子图演示了旋转曲面的生成过程。
第一个子图展示了两条空间直线------蓝色z轴直线和红色对角线直线,并绘制了z轴绕对角线旋转12个不同角度时的绿色轨迹线,直观呈现旋转的动态过程。
第二个子图则基于Rodrigues旋转公式,通过网格化参数计算并绘制出完整的旋转曲面:一个由z轴绕对角线(方向向量[1,1,1])连续旋转形成的青色半透明曲面。
代码在曲面上保留了原始直线和旋转轴,添加了黑色轮廓线以增强立体感,并设置了合适的三维视角、光照效果和颜色条,最终形成一个展示直线绕空间轴旋转生成曲面的完整教学可视化图形。