
🔥小龙报:个人主页
🎬作者简介:C++研发,嵌入式,机器人方向学习者
❄️个人专栏:《算法通关指南》
✨ 永远相信美好的事情即将发生

文章目录
前言
本专栏聚焦算法题实战,系统讲解算法模块:以《c++编程》,《数据结构和算法》《基础算法》《算法实战》 等几个板块以题带点,讲解思路与代码实现,帮助大家快速提升代码能力
ps:本章节题目分两部分,比较基础笔者只附上代码供大家参考,其他的笔者会附上自己的思考和讲解,希望和大家一起努力见证自己的算法成长
一、差分
前缀和与差分的核心思想是预处理,可以在暴力枚举的过程中,快速给出查询的结果,从而优化时间复杂度,是经典的用空间替换时间的做法。
本质 :前缀和与差分是⼀对互逆的运算。
二、一维差分
2.1 差分数组构建方式
根据定义 : f[i]=a[i]−a[i−1]
根据差分数组的性质 : f[i] += a[i], f[i+1] −= a[i]

2.2 根据差分数组的性质处理区间修改
核心公式 :f[L] + = c, f[R+1] − = c
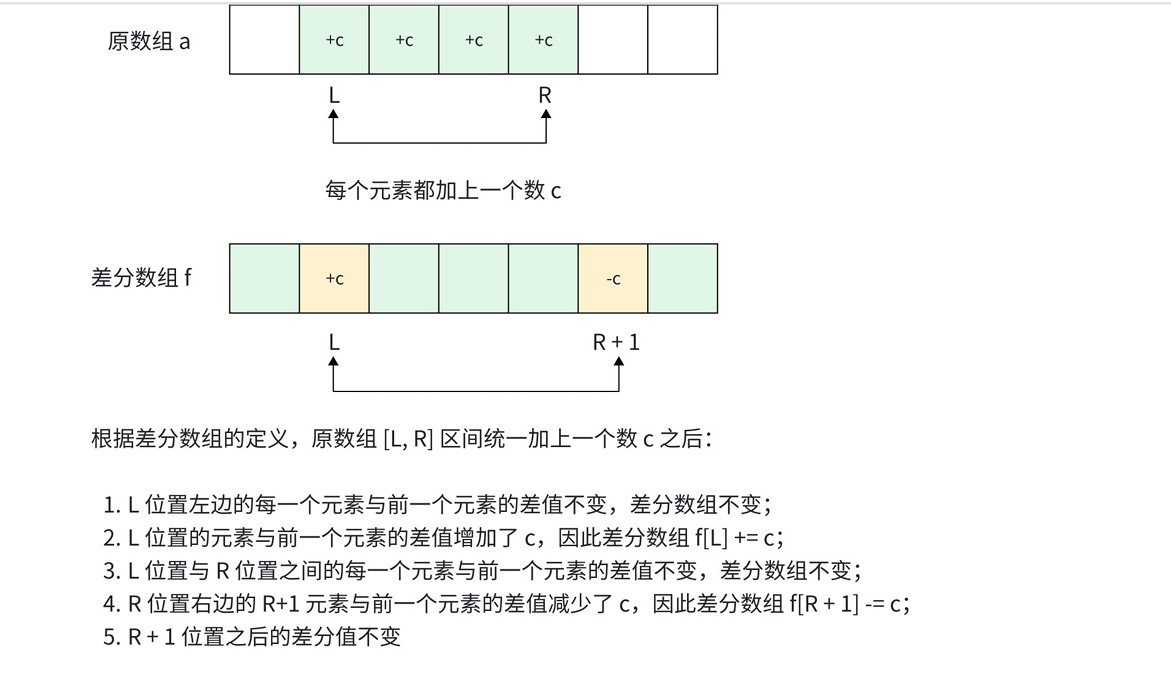
2.3 还原数组
对差分数组做⼀次「前缀和」,就可以还原出原数组

三、一维差分经典算法题
3.1【模板】差分
3.1.1题目
链接:【模板】差分
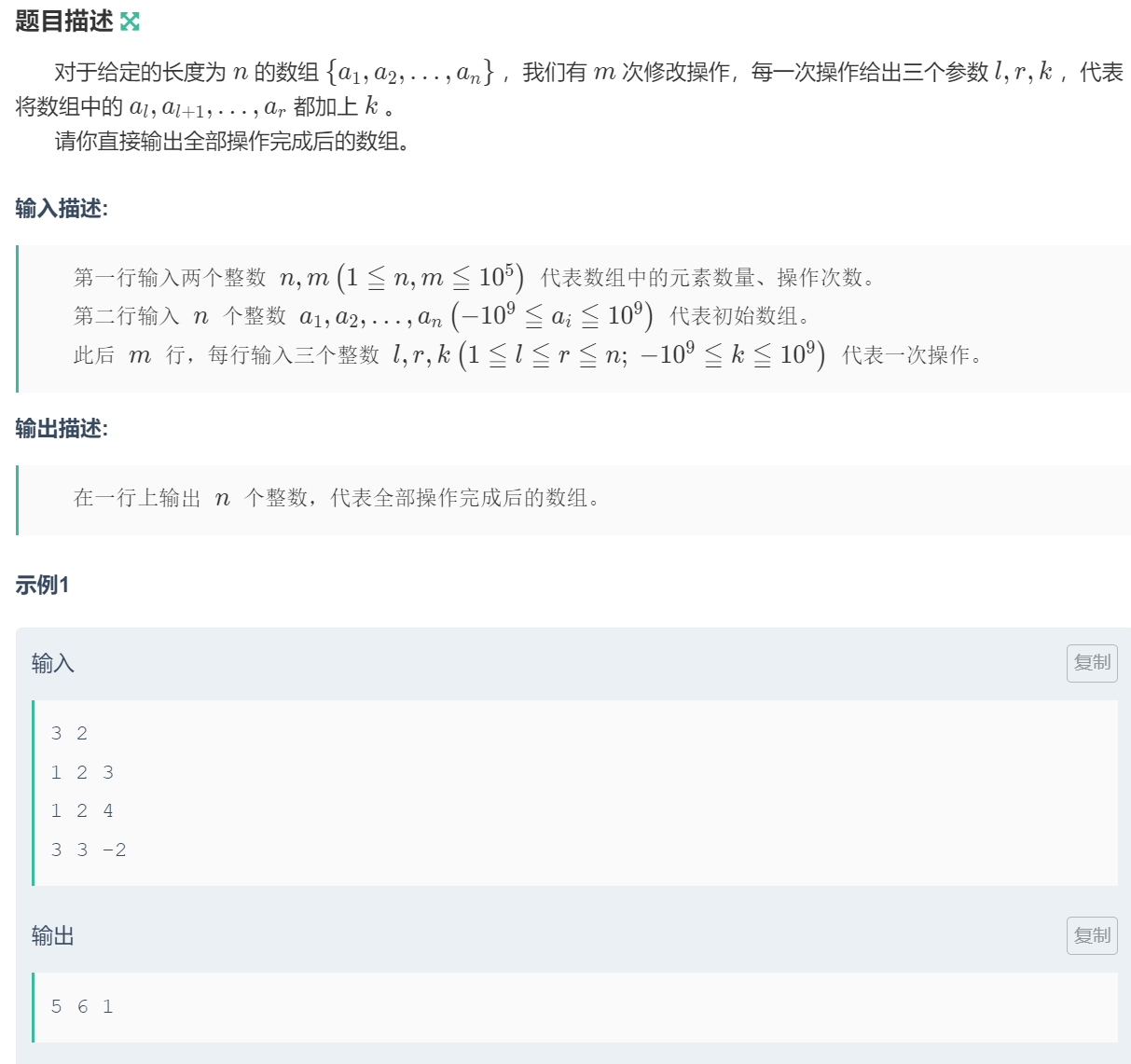
3.1.2 算法原理
依照刚才讲解一维差分原理模拟即可
3.1.3代码
3.1.3.1 根据差分数组的性质
c
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
int x;
cin >> x;
f[i] += x;
f[i + 1] -= x;
}
while (m--)
{
int l, r, k;
cin >> l >> r >> k;
f[l] += k;
f[r + 1] -= k;
}
for (int i = 1; i <= n; i++)
{
f[i] += f[i - 1];
cout << f[i] << " ";
}
return 0;
}3.1.3.2 根据定义
c
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int f[N];
int a[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= n; i++)
f[i] = a[i] - a[i - 1];
while (m--)
{
int l, r, k;
cin >> l >> r >> k;
f[l] += k;
f[r + 1] -= k;
}
for (int i = 1; i <= n; i++)
{
f[i] += f[i - 1];
cout << f[i] << " ";
}
return 0;
}3.2 海底高铁
3.2.1题目
链接:海底高铁
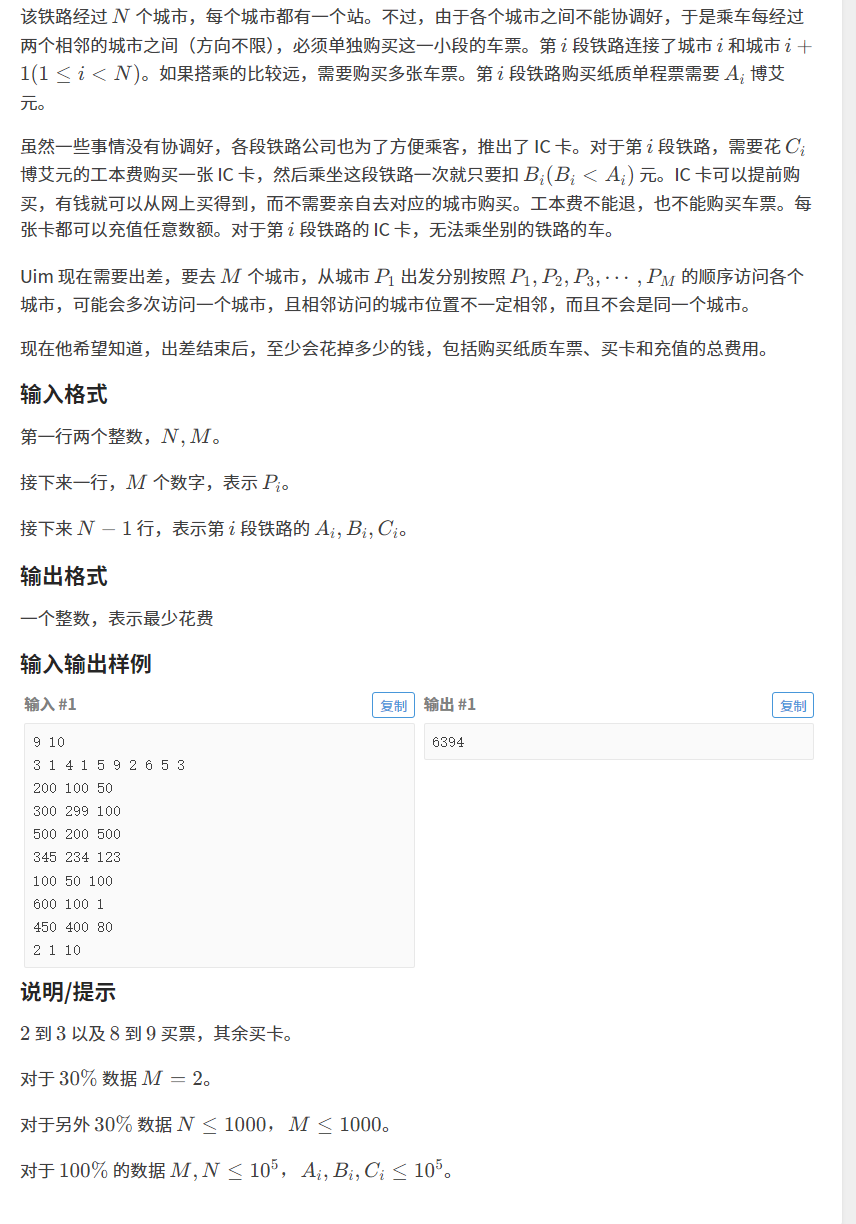
3.2.2 算法原理
1.先考虑如何让花费最小,想要求最小花费,需要知道每⼀段高铁被「乘坐了多少次」,记作f[i],那么最小花费就是「买票的花费」与「买卡的花费」两者之间的最小值:f[i]
(1)买票花费:;a[i]×f[i]
(2)买卡花费,乘车花费+工本费:b[i]×f[i]+c[i]
(3)那么最小花费就是:mincost=min(a[i]×f[i], b[i]×f[i]+c[i])
2.接下来考虑如何求出每⼀段⾼铁被「乘坐了多少次」。根据访问城市的序列p1 ,p2 ,p3 ,...,pm 可知,对于任意⼀次访问 pi∼p ,我们会乘坐[pi ~ pi + 1 - 1]之间所有的高铁,比如p =i 3, pi+1 = 6,那么[3,5]之间所有的高铁都会被乘坐⼀次,相当于每个数都加上1,「注意6位置不会乘坐到」。那么我们就可以利用「差分数组」
(1)创建⼀个全为0的差分数组;
(2)遍历访问序列,对于每⼀次访问f[p]+ i +, f[p]− i+1 −
(3)然后对差分数组做⼀次前缀和,就得到每个⾼铁乘坐的次数
注意城市访问的序列有可能pi > pi + 1,此时应该「交换」⼀下顺序
3.2.3代码
c
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL f[N];
int main()
{
LL n, m;
cin >> n >> m;
LL x;
cin >> x;
for (int i = 2; i <= m; i++)
{
LL y;
cin >> y;
// x -> y
if (y > x)
{
f[x]++;
f[y]--;
}
// y -> x
else
{
f[x]--;
f[y]++;
}
x = y;
}
for (int i = 1; i < n; i++)
f[i] += f[i - 1];
LL ret = 0;
for (int i = 1; i < n; i++)
{
LL a, b, c;
cin >> a >> b >> c;
ret += min(a * f[i], c + b * f[i]);
}
cout << ret << endl;
return 0;}
总结与每日励志
✨ 摘要: 本文介绍了差分算法的基本原理及其应用,重点讲解了一维差分的构建方式、区间修改处理及数组还原方法。通过经典算法题如【模板】差分和海底高铁问题,展示了差分在优化时间复杂度中的实际应用。文章还提供了详细的代码实现,帮助读者快速掌握差分算法。最后以励志语句"永远相信美好的事情即将发生"鼓励读者坚持学习与成长。 关键词: 差分算法、前缀和、区间修改、时间复杂度、算法实战
