引言
在计算机科学中,查找算法是一类基础且关键的算法,广泛应用于各类应用中,例如数据库检索、信息处理、路由算法等。数据的查找问题是非常常见的,不论是在数据库、文件系统,还是在内存中的数据访问,都离不开高效的查找算法。本篇文章将从查找算法的基础概念出发,结合经典的查找算法进行深入分析,并通过实际代码进行演示,帮助大家更好地理解和应用查找算法。
一、查找算法的分类
查找算法主要分为两大类:线性查找 (也叫顺序查找)和非线性查找(例如二分查找、哈希查找等)。根据查找过程中数据的存储方式与特点,查找算法的效率和适用场景有所不同。
1. 线性查找(顺序查找)
线性查找是最简单的查找算法。其基本思路是从数据集合的第一个元素开始,逐一比较目标值与每个元素,直到找到目标元素或遍历完所有元素为止。线性查找的时间复杂度为 O(n),适用于数据没有任何排序的情况。
适用场景:
-
数据是无序的,无法通过其他高效算法进行优化。
-
查找的数据量较小,线性查找的性能开销不大。
代码实现:
#include <iostream>
using namespace std;
int linearSearch(int arr[], int size, int target) {
for (int i = 0; i < size; ++i) {
if (arr[i] == target) {
return i; // 返回找到的元素索引
}
}
return -1; // 未找到目标元素
}
int main() {
int arr[] = {5, 3, 7, 2, 8, 6};
int target = 8;
int size = sizeof(arr) / sizeof(arr[0]);
int result = linearSearch(arr, size, target);
if (result != -1)
cout << "元素 " << target << " 的索引是: " << result << endl;
else
cout << "未找到元素 " << target << endl;
return 0;
}控制台代码实现: 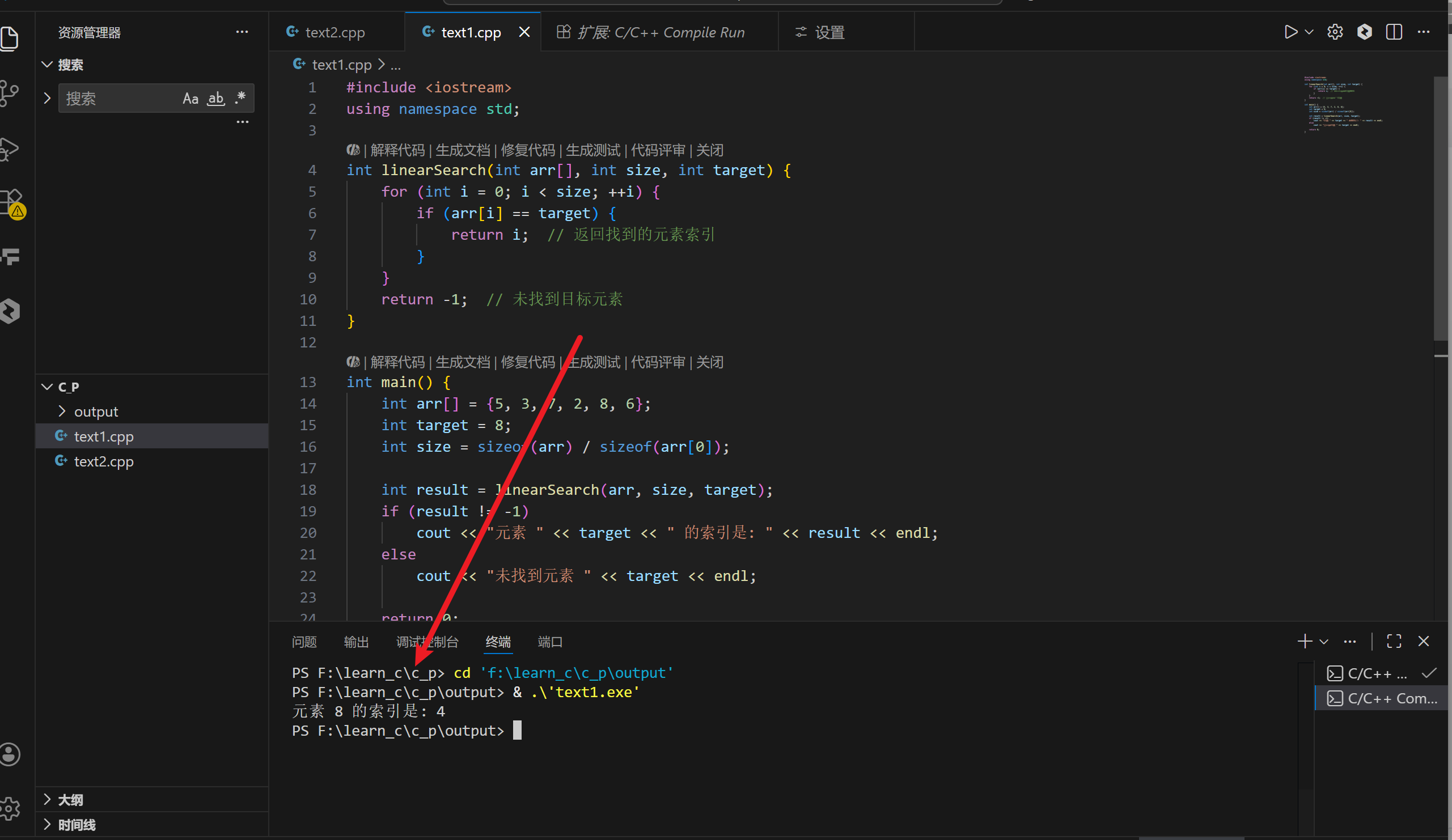
系统终端代码实现:
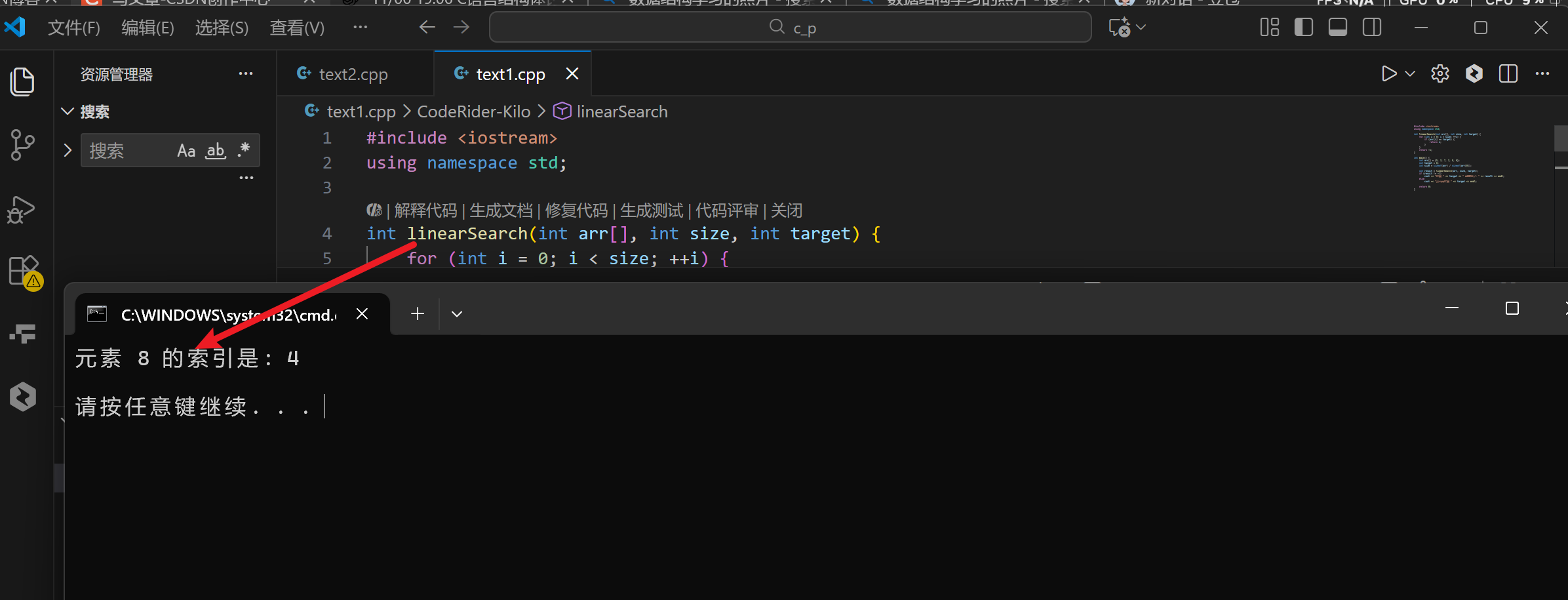
注意:在系统终端上通常会中文乱码解决方法:(明天写)
2. 二分查找
二分查找是一种更高效的查找算法。其前提是数据集合必须是有序的。二分查找通过将查找区间不断折半,迅速缩小查找范围,极大提高了查找效率。二分查找的时间复杂度为 O(log n)。
适用场景:
-
数据已经排好序。
-
查找操作频繁,要求更高的性能。
代码实现:
#include <iostream>
using namespace std;
int binarySearch(int arr[], int size, int target) {
int low = 0, high = size - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
if (arr[mid] == target) {
return mid; // 找到目标元素
}
if (arr[mid] < target) {
low = mid + 1; // 目标在右半部分
} else {
high = mid - 1; // 目标在左半部分
}
}
return -1; // 未找到目标元素
}
int main() {
int arr[] = {2, 3, 5, 6, 7, 8};
int target = 6;
int size = sizeof(arr) / sizeof(arr[0]);
int result = binarySearch(arr, size, target);
if (result != -1)
cout << "元素 " << target << " 的索引是: " << result << endl;
else
cout << "未找到元素 " << target << endl;
return 0;
}控制台代码实现:
3. 哈希查找
哈希查找是一种基于哈希表的数据结构来实现查找的方法。通过哈希函数,将元素映射到哈希表的特定位置,可以在常数时间 O(1) 内完成查找操作。哈希查找广泛应用于数据库索引、缓存等场景。
适用场景:
-
数据量大,且查找操作非常频繁。
-
哈希表能有效避免冲突,或者冲突可通过链表、开放地址等策略解决。
代码实现:
#include <iostream>
#include <unordered_map>
using namespace std;
int main() {
unordered_map<int, string> hashTable;
hashTable[1] = "One";
hashTable[2] = "Two";
hashTable[3] = "Three";
int key = 2;
if (hashTable.find(key) != hashTable.end()) {
cout << "元素 " << key << " 的值是: " << hashTable[key] << endl;
} else {
cout << "元素 " << key << " 未找到" << endl;
}
return 0;
}控制台代码实现:
三、查找算法的优缺点比较
| 查找算法 | 时间复杂度 | 空间复杂度 | 适用场景 | 优点 | 缺点 |
|---|---|---|---|---|---|
| 线性查找 | O(n) | O(1) | 无序数据、小规模查找 | 实现简单,无需排序 | 数据量大时性能差,效率低 |
| 二分查找 | O(log n) | O(1) | 已排序的数据 | 高效、查找速度快 | 需要数据预先排序,不能用于无序数据 |
| 哈希查找 | O(1) | O(n) | 查找频繁、数据量大 | 查找速度快,适合大规模数据 | 哈希冲突需要解决,占用额外空间 |
查找算法的选择
-
线性查找:适用于小规模的无序数据,或者一次性查找不多的场景。其优势是简单且不需要额外的数据结构。
-
二分查找:适用于已经排序好的数据,尤其在需要频繁查询的场景下,能够提供更高的性能。使用二分查找时,务必保证数据的有序性。
-
哈希查找:适用于需要快速查找、插入和删除操作的大规模数据,尤其在内存中查找时,非常高效。哈希查找的优势在于其常数时间复杂度,但需要处理哈希冲突,且会占用额外的空间。
四、查找算法的优化策略
1. 数据预处理
数据的预处理可以显著提高查找效率。对于需要频繁查找的场景,提前将数据排序或构建哈希表,能够大幅减少查找的时间复杂度。
2. 使用并行算法
在面对海量数据时,单线程查找可能会变得非常慢。可以考虑使用并行算法,将查找操作分配到多个线程中,充分利用多核CPU的优势。
3. 适时转换查找算法
如果数据集合发生变化,例如频繁的插入和删除操作,可能会导致二分查找或哈希查找的效率下降。这时可以通过动态选择不同的查找算法(如切换为平衡树、B树等)来提高查找效率。
五、实践总结与展望
查找算法是编程中非常基础且常见的操作。不同的查找算法适用于不同的应用场景,合理选择查找算法可以有效提升系统的性能。在实际开发中,除了考虑算法本身的时间复杂度外,还需要结合具体的应用场景来选择合适的查找策略。随着数据量的增加,算法的选择和优化显得尤为重要。
通过这篇文章的学习和实践,我更加深刻地理解了各种查找算法的实现与优化,希望大家能够在实际开发中灵活运用这些算法,提升应用程序的性能。
我创了个CSDN交流群加微信+www13526323270