激光雷达点云拟合中的ICP（迭代最近点）算法

激光雷达点云拟合中的ICP（迭代最近点）算法 ，是用于将两个不同视角下的点云数据精确对齐（配准） 的核心算法。其核心思想是通过迭代，不断寻找两个点云之间最近的点对，并计算最优的刚性变换（旋转 + 平移），最终使它们重合。

ICP 算法核心步骤

给定源点云 P 和目标点云 Q ，经典的 点到点 ICP 算法流程如下：

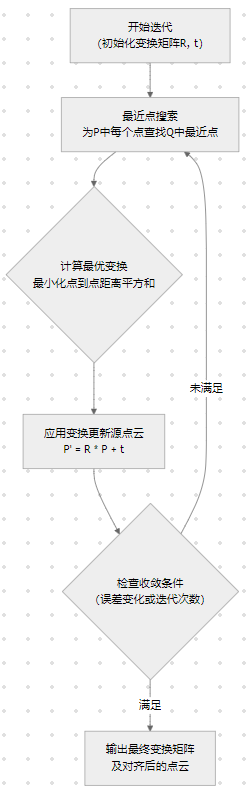
步骤详解：

最近点搜索 ：对源点云 P 中的每一个点，在目标点云 Q 中寻找欧氏距离最近的点，建立点对对应关系。
计算最优变换 ：基于当前匹配的点对，求解一个刚性变换 （旋转矩阵 R 和平移向量 t ），使得所有对应点对之间的距离平方和最小 。这通常通过 SVD（奇异值分解） 或 四元数法 求解。
应用变换 ：使用计算得到的 R 和 t 对源点云 P 进行变换，得到新的源点云 P' = R * P + t。
判断收敛 ：计算变换后点云与目标点云的均方误差。若误差小于设定阈值，或两次迭代间的误差变化很小，或达到最大迭代次数，则停止迭代；否则，返回步骤1继续。

MATLAB 实现与代码

MATLAB 提供了强大的点云处理工具箱，实现 ICP 主要有两种方式：

方法一：使用内置函数 `pcregistericp` (最便捷)

matlab 复制代码

% 读取或生成源点云和目标点云（示例）
% ptCloudSource = pcread('source.ply');
% ptCloudTarget = pcread('target.ply');

% 创建示例点云（一个简单的平面点云，并施加一个变换）
target = pointCloud([rand(1000,2), zeros(1000,1)]); % 目标：XY平面点云
source = pointCloud([rand(1000,2), zeros(1000,1)]); % 源：另一个XY平面点云

% 人为给源点云施加一个变换，模拟不同视角
angle = pi/8; % 旋转45度
R = [cos(angle) -sin(angle) 0; sin(angle) cos(angle) 0; 0 0 1];
t = [0.5, 0.2, 0];
sourceTransformed = pctransform(source, rigid3d(R, t));

% 执行ICP配准
[tform, movingReg, rmse] = pcregistericp(sourceTransformed, target, ...
    'Metric', 'pointToPoint', ... % 使用'pointToPlane'通常更快更鲁棒
    'MaxIterations', 100, ...
    'Tolerance', [0.01, 0.001]); % 绝对误差容限和相对误差容限

% 显示结果
disp('变换矩阵：');
disp(tform.T); % 4x4齐次变换矩阵
disp(['均方根误差（RMSE）: ', num2str(rmse)]);

% 可视化
pcshowpair(movingReg, target, 'VerticalAxis', 'Y', 'VerticalAxisDir', 'Down')
title('ICP配准结果');
xlabel('X'); ylabel('Y'); zlabel('Z');

方法二：手动实现核心的SVD求解 (理解原理)

matlab 复制代码

function [R, t, transformedP] = myPointToPointICP(P, Q, maxIter, tolerance)
% 简化的手动ICP实现（点到点）
% 输入: P-源点云（Nx3）， Q-目标点云（Mx3）
% 输出: R-旋转矩阵（3x3）， t-平移向量（1x3）， transformedP-变换后的P

    R = eye(3);
    t = zeros(1, 3);
    prevError = inf;

    for iter = 1:maxIter
        % 1. 最近邻搜索（这里用简单循环示意，实际应用应使用KD树加速）
        indices = knnsearch(Q, P * R' + t); % 使用MATLAB的knnsearch
        Q_matched = Q(indices, :);

        % 2. 去中心化
        centroid_P = mean(P, 1);
        centroid_Q = mean(Q_matched, 1);
        P_centered = P - centroid_P;
        Q_centered = Q_matched - centroid_Q;

        % 3. 使用SVD计算最优旋转
        H = P_centered' * Q_centered; % 3x3协方差矩阵
        [U, ~, V] = svd(H);
        R_new = V * U';

        % 确保是右手系的旋转（防止镜像）
        if det(R_new) < 0
            V(:,3) = -V(:,3);
            R_new = V * U';
        end

        % 4. 计算平移
        t_new = centroid_Q' - R_new * centroid_P';

        % 5. 应用变换并更新
        R = R_new * R;
        t = (R_new * t' + t_new)';

        % 6. 计算误差
        transformedP = P * R' + t;
        currError = mean(sqrt(sum((transformedP - Q_matched).^2, 2)));

        % 7. 检查收敛
        if abs(prevError - currError) < tolerance
            fprintf('在 %d 次迭代后收敛。\n', iter);
            break;
        end
        prevError = currError;
    end
    fprintf('最终误差: %f\n', prevError);
end

ICP 变体算法对比

根据匹配准则和优化目标的不同，ICP有多种改进变体，下表列出了常见的几种：

变体名称	匹配准则/优化目标	优点	缺点/适用场景
Point-to-Point	最小化点到点距离平方和	原理简单，直观，MATLAB内置支持	对初始位置敏感，收敛慢，易陷入局部最优
Point-to-Plane	最小化源点到目标点切平面的距离	收敛更快，收敛域更大，更常用	需要目标点云的法向量，对法向估计敏感
Plane-to-Plane	最小化局部平面之间的距离	精度可能更高，对噪声鲁棒性更好	计算复杂，需要估计两片点云的法向和曲率
颜色/特征信息辅助	结合点颜色、法向、FPFH等特征进行匹配	在特征丰富场景下匹配更准确	对特征提取质量依赖高，计算量增大

在MATLAB中调用Point-to-Plane ICP：

matlab 复制代码

% 首先需要计算目标点云的法向量
target = pcdownsample(target, 'gridAverage', 0.01); % 可先下采样
normals = pcnormals(target); % 计算法向量
target.Normal = normals;

% 然后使用'pointToPlane'度量
[tform, movingReg] = pcregistericp(source, target, 'Metric', 'pointToPlane');

参考代码激光雷达点云数据拟合点云拟合icp算法 www.youwenfan.com/contentcsn/83727.html

总结来说，对于激光雷达点云，Point-to-Plane ICP 通常是更优选择。在MATLAB中，优先使用内置的pcregistericp函数，它经过高度优化并支持多种变体。理解其原理有助于你根据具体的点云特征（稀疏度、噪声水平、重叠区域大小）调整参数，获得稳健的配准结果。

激光雷达点云拟合中的ICP（迭代最近点）算法

ICP 算法核心步骤

MATLAB 实现与代码

方法一：使用内置函数 pcregistericp (最便捷)

方法二：手动实现核心的SVD求解 (理解原理)

ICP 变体算法对比

方法一：使用内置函数 `pcregistericp` (最便捷)