文章目录
前言
本文介绍了使用拉链法解决哈希冲突的实现方法。主要内容包括:1)拉链法的基本概念,将同义词存储在链表中;2)插入操作流程,通过散列函数计算地址并插入链表;3)查找操作步骤,计算地址后顺序查找链表,并分析了查找长度的统计标准;4)删除操作过程,查找成功后从链表中移除元素;5)优化建议,如采用有序链表提升查找效率。文章通过具体示例详细演示了各操作的实现过程,并附有可视化算法网站链接。适用于需要理解哈希表冲突解决方法的读者。
一.基本概念
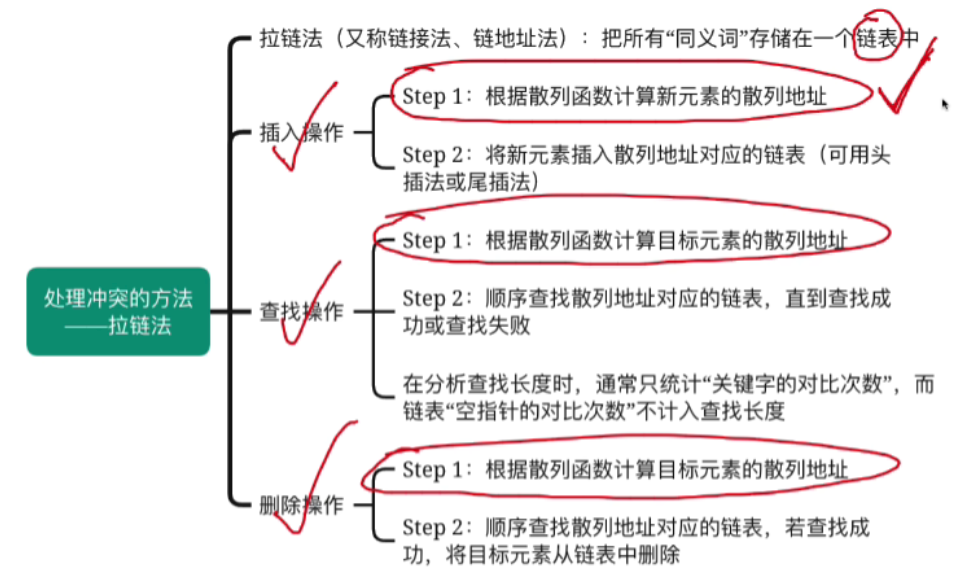
- 拉链法(又称链接法、链地址法):把所有"同义词"存储在一个链表中
二.散列表的插入操作(拉链法解决冲突)
1.思路
- 结合散列函数计算新元素的散列地址
- 将新元素插入散列地址对应的链表(可用头插法,也可用尾插法)
2.具体例子
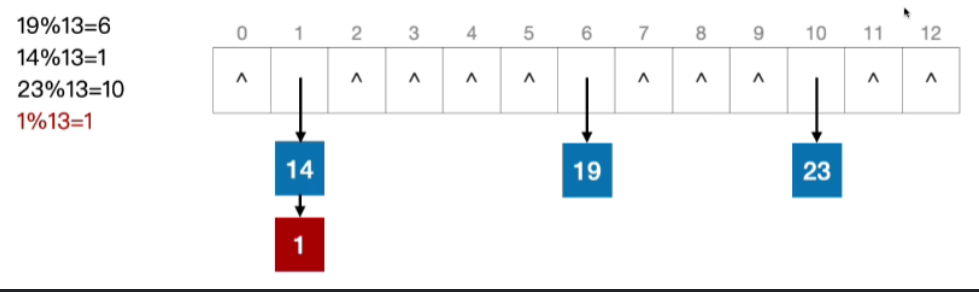
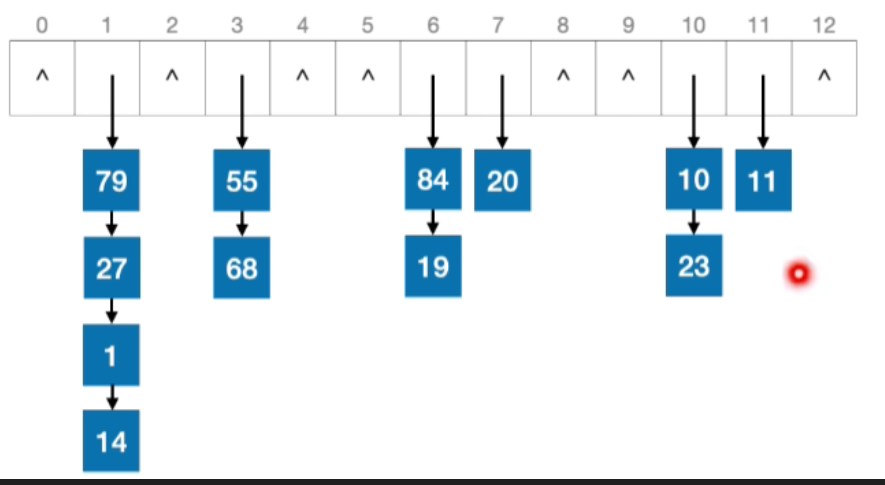
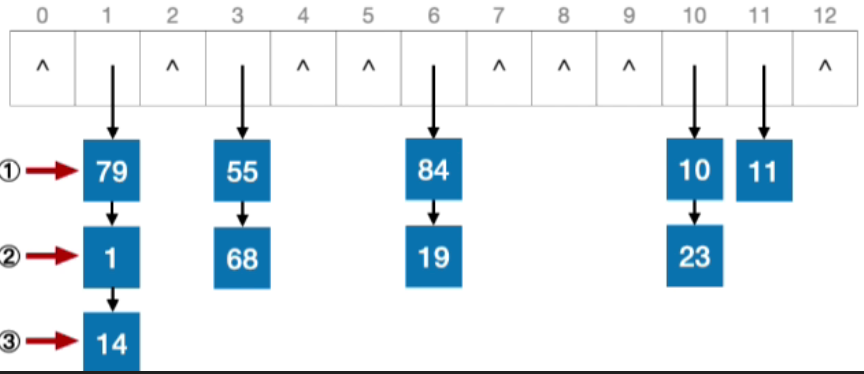
- 例:若散列表长度为13,散列函数 H(key)=key%13,用拉链法解决冲突。依次插入关键字{19, 14, 23, 1, 68, 20, 84, 27, 55, 1, 10, 79}

- 可以将0-12视为13个链表的头指针
- 计算出所有元素的散列地址

- 根据计算出的散列地址,依次插入19,14,23
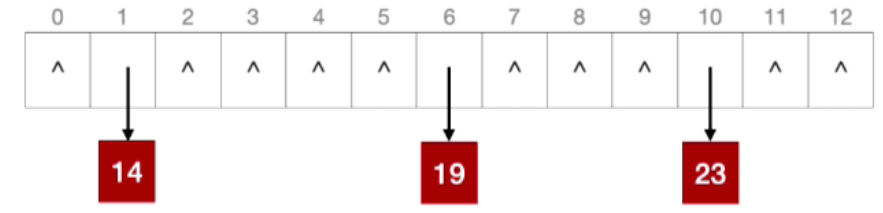
- 接下来插入13,发现13的地址也是1,那么使用头插法插入到14的上面,68,20和1也是类似的方法
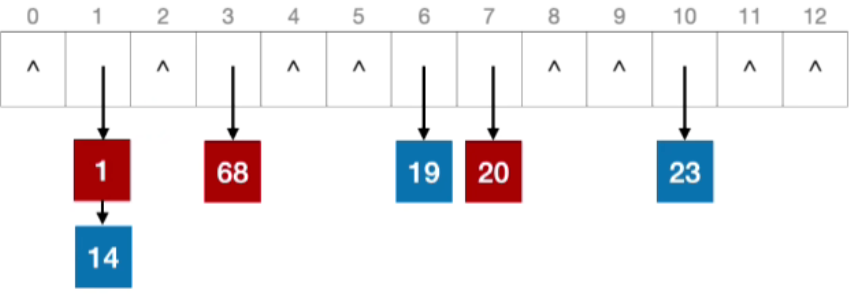
- 之后也是类似,不再赘述
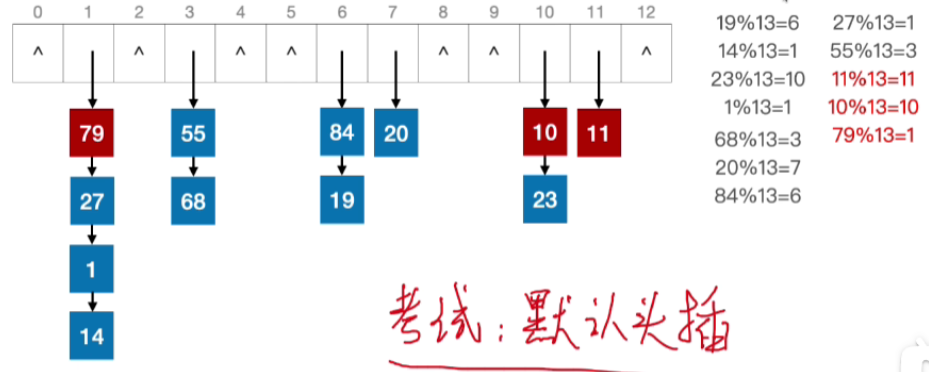
三.散列表的查找操作(拉链法解决冲突)
1.思路
- 根据散列函数计算目标元素的散列地址
- 顺序查找散列地址对应的链表,直到查找成功或查找失败
- 在分析查找长度时,通常只统计"关键字的对比次数",而链表"空指针的对比次数"不计入查找长度
2.具体例子
- 例:若散列表长度为13,散列函数H(Key)=key%13,用拉链法解决冲突。在下述散列表中依次查找元素27,20,66,21,分析每次查找操作的过程和查找长度。
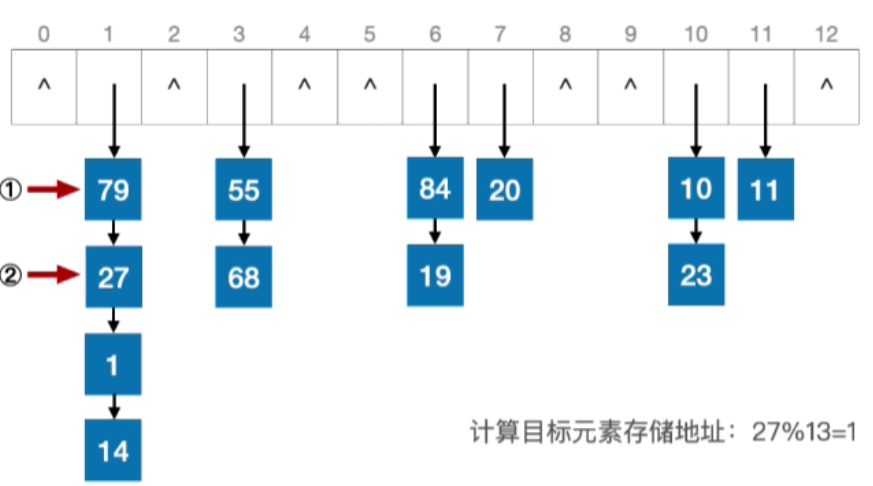
- 计算目标元素存储地址:27%13=1,27查找成功,查找长度=2
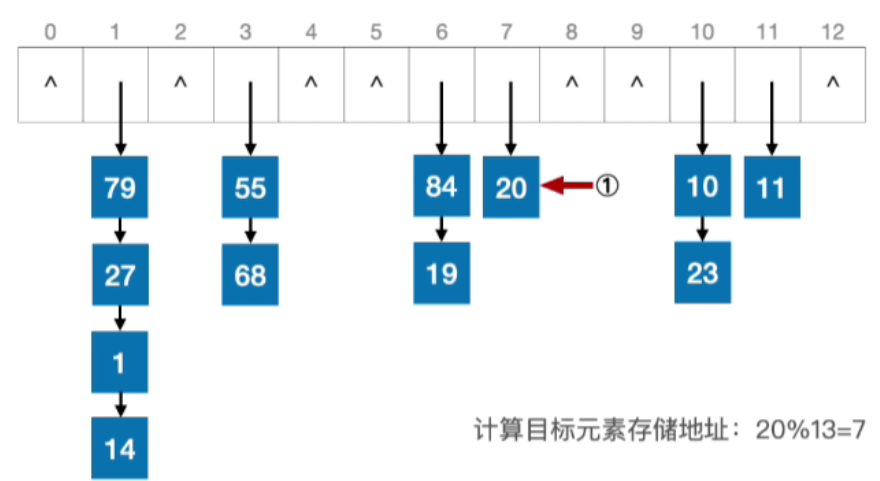
- 计算目标元素存储地址:20%13=7,20查找成功,查找长度=1
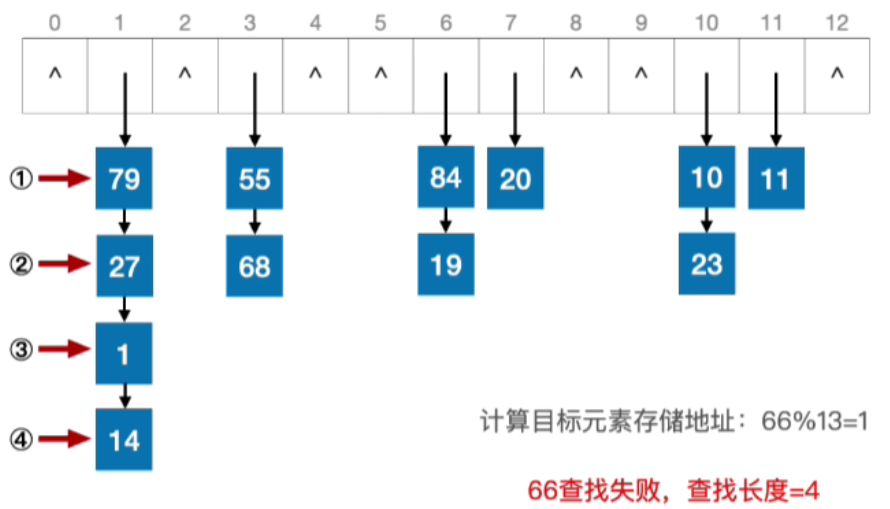
- 接下来查找66,计算目标元素存储地址:66%13=1,依次对比链表当中的所有元素,最后并没有在链表中找到关键字66,因此查找完整个链表,我们就可以确定66这个元素查找失败,查找长度=4
- 计算目标元素存储地址:21%13=8,8这个位置它是一个空链表,这只保存了一个空指针,那到此为止可以确定21这个元素查找失败,查找长度=0(在8这个位置我们只是对比了一个空指针,并不是对比关键字的值,因此空指针的对比并不会计入查找长度)
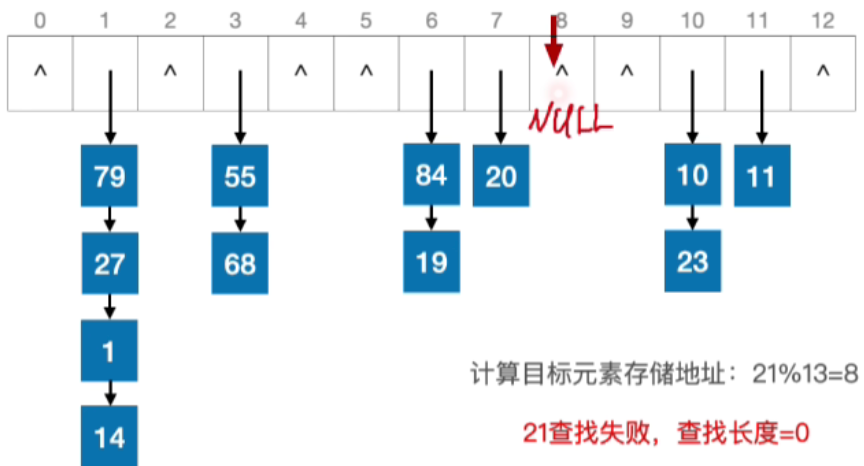
注:有的教材会把"空指针的对比"也计入查找长度。但考试中默认只统计"关键字对比次数"。
四.散列表的删除操作(拉链法解决冲突)
1.思路
- 根据散列函数计算目标元素的散列地址
- 顺序查找散列地址对应的链表,若查找成功,将目标元素从链表中删除
2.具体例子
- 例:若散列表长度为13,散列函数 H(k(key)=key%13,用拉链法解决冲突。在下述散列表中依次删除元素 27,20,66。
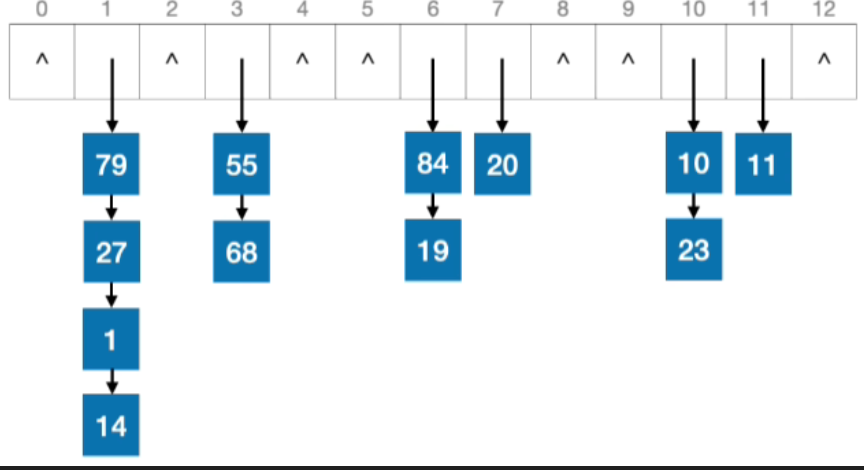
- 计算目标元素存储地址:27%13=1,先查找到目标元素,再直接将其从链表中删除
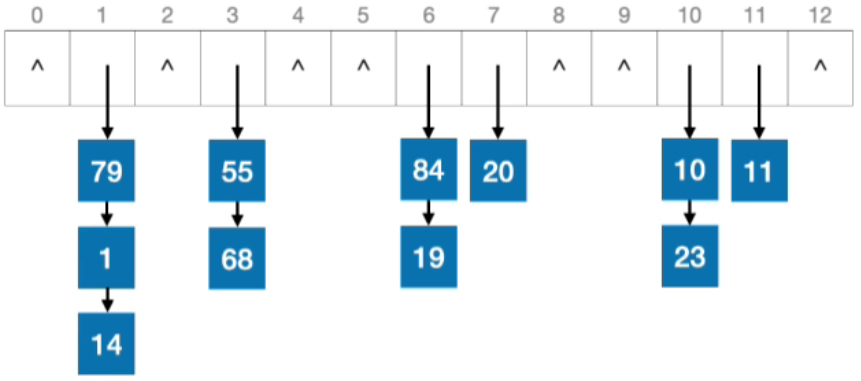
- 计算目标元素存储地址:20%13=7,接下来在7这个列表中找到目标元素,发现20是唯一的一个元素,所以将7这个链表指针设为空
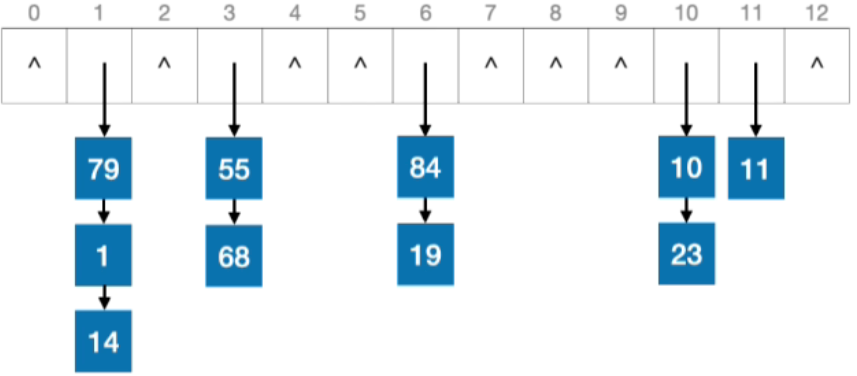
- 计算目标元素存储地址:66%13=1,由于在1这个链表当中没有找到66这个元素,所以此次删除操作失败
五.知识回顾与重要考点
算法网站链接:
OpenHashing
六.拓展:插入操作的小优化
- 新元素用"头插法"插入链表,每个链表是乱序的。
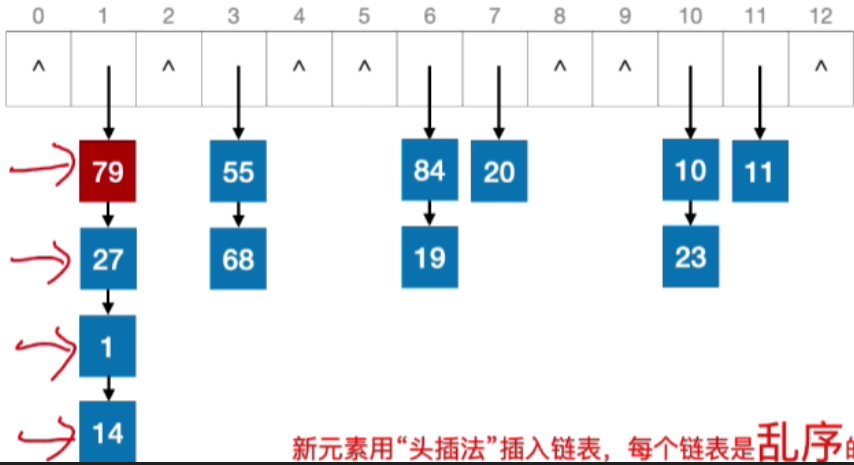
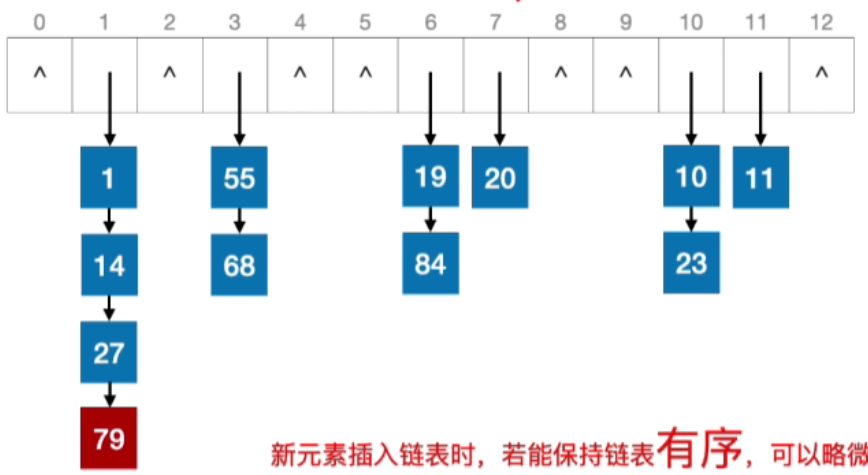
- 新元素插入链表时,若能保持链表有序,可以略微提高"查找"效率。
结语
一更😉,最近段更了一段时间,因为我这边着实太忙了
如果想查看更多章节,请点击:一、数据结构专栏导航页