【RL】DAPO详解2

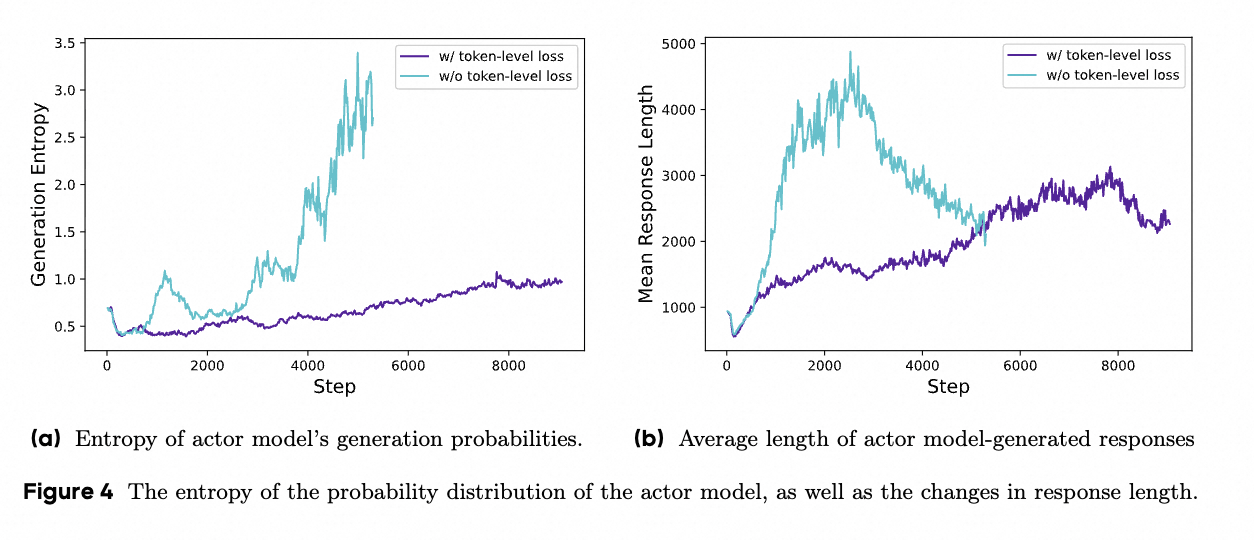
图 4 在论文中用于对比 "有无 token-level policy gradient loss" 时训练过程中两个关键量的演化：生成概率的熵（entropy）和平均响应长度（mean response length）。我先把论文用来描述 token-level loss 的目标式（简化形式）写出，便于后面说明其机制：
Jtoken-level(θ)=E[1P∑i=1G∑t=1∣oi∣min⁡ ⁣(ri,tA^i,t,  clip⁡(ri,t,1−ϵlow,1+ϵhigh)A^i,t)], J_{\text{token-level}}(\theta)=\mathbb{E}\Big[\frac{1}{P}\sum_{i=1}^G\sum_{t=1}^{|o_i|} \min\!\big(r_{i,t}\hat A_{i,t},\;\operatorname{clip}(r_{i,t},1-\epsilon_{\text{low}},1+\epsilon_{\text{high}})\hat A_{i,t}\big)\Big], Jtoken-level(θ)=E[P1i=1∑Gt=1∑∣oi∣min(ri,tA^i,t,clip(ri,t,1−ϵlow,1+ϵhigh)A^i,t)],

其中 P=∑i∣oi∣P=\sum_i|o_i|P=∑i∣oi∣ 是组内总 token 数，ri,tr_{i,t}ri,t 是重要性比，A^i,t\hat A_{i,t}A^i,t 是组内归一化的奖励优势。

基于这一定义，图 4 的两条子图说明如下要点：

• 子图 (a) --- 生成概率的熵（Entropy）：

  图中对比了"有 token-level loss（w/ token-level loss）"与"无 token-level loss（w/o token-level loss）"两种训练下 actor 模型生成分布的熵随训练步数的变化。论文指出和图示一致的结论是：

  • 在没有 token-level loss（即采用 sample-level 平均损失）的情况下，熵更容易不受控地上升或出现异常（表示模型生成分布变得非常平坦或产生大量低质量、高多样性的输出------如胡言乱语、重复等）。
  • 加入 token-level loss 后，熵的增长被抑制/更平稳，模型在保持适度探索的同时避免过度的无序生成。
    直观原因：token-level loss 将每个 token 的贡献都显式计入，使得对于产生低质量但超长响应的"坏模式"可以在 token 级别被更精确地惩罚，从而抑制那些会人为提高熵但不提高任务回报的生成模式。

• 子图 (b) --- 平均响应长度（Mean Response Length）：

  这张子图展示的是两种训练下模型生成的平均 token 长度随训练步数的变化。结论是：

  • 无 token-level loss 时，响应长度往往会"非健康地"快速增长（模型通过变长生成来获得某些奖励或逃避惩罚），但这些变长并不一定对应更高质量的推理；长序列里可能充斥重复或无意义片段。
  • 使用 token-level loss 后，长度增长更"健康、可控"------即当模型真正学到有效的长链式推理时长度会合理增长，但不会被无意义的延长行为占据。
    原因同样是 credit assignment：token-level loss 不把长序列的"平均化"稀释掉每个 token 的惩罚/奖励，因而可以更好地压制长但低质的生成，鼓励真正有价值的长推理。

总结一句话的直觉：样本级（sample-level）先把一条长回复内部的 token 平均，这会稀释对长回复中"坏 token" 的惩罚，从而容忍甚至鼓励生成冗长但低质的序列；而 token-level loss 把每个 token 当作独立贡献单位来评估和优化，所以能更精细地约束生成质量，表现为图 4 中较稳的 entropy 曲线和更健康的长度曲线。

工程与实践提示（由图 4 的含义延伸）：

• 实现时要在 token 级别保存并重算每个 token 的 log-prob、mask 掉 padding，再按 PPP 做归一化，代价是计算与内存开销增大。
• 为避免噪声放大，仍需对组内 advantage 做数值保护（如 σ←max⁡(σ,ε)\sigma\leftarrow\max(\sigma,\varepsilon)σ←max(σ,ε)）并可对 A^\hat AA^ 做 clipping。
• 可做的后续实验：不同 token 权重方案（均权、按位置信息加权、按置信度加权）、token-level 与 sample-level 的混合损失、以及在 token-level 基础上引入 token-wise value 模型以进一步精细化 credit assignment。

如果你想，我可以：

• 给出把 sample-level 换成 token-level 的具体伪代码（显示如何保存 old log-probs、重算 new log-probs、按 token 累积 surrogate 并归一化）；或
• 把图 4 的曲线用示例数据重现，帮助你直观看出两者差异。你想先看哪一个？

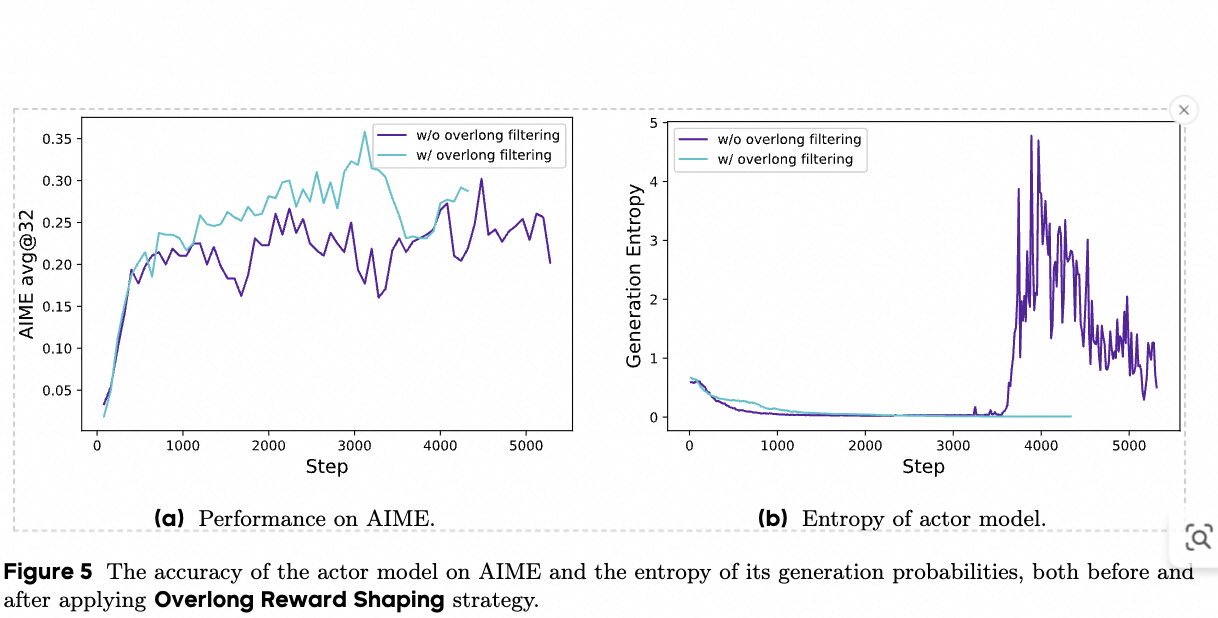
好，我来逐条、深入地解释论文中图 5（Figure 5）在说什么、为什么会出现这样的现象、它背后的机制是什么，以及在实现上和后续实验中应该注意/可尝试的事项。会引用论文中的 Overlong Reward Shaping（过长奖励塑造）相关公式并给出实现建议。所有含公式的句子我都用 LaTeX 格式写出。

一、图 5 的组成与直接结论

• 图 5(a) 比较了在训练过程中，有无对被截断（overlong）样本进行过滤（Overlong Filtering）时，在 AIME 验证集上的准确率曲线差异。结论是：采用 overlong filtering 能显著稳定训练并提升最终准确率。
• 图 5(b) 比较了相同设置下 actor 模型生成分布的熵（entropy）。结论是：采用 overlong filtering 后，熵更低且曲线更平稳，说明模型生成分布更稳健、不至于变得过度杂乱或无意义。

二、为什么"过长样本的奖励处理"会影响训练（原因与机制）

• 在强化学习训练中，若生成被强制截断（因为超过最大长度 Lmax⁡L_{\max}Lmax），通常会对该样本给出惩罚或低分。这种做法会把"长度造成的截断"与"推理质量"混为一谈：一个本来推理正确但确实较长的样本，会因为被截断而被赋低 reward，从而把正确的推理模式误判为坏模式，给模型提供误导性的负信号。
• 这种误导性信号会产生"reward noise" ------ 即奖励不再能可靠反映推理质量，导致优势估计 A^\hat AA^ 变噪声大或方差增大，进而使梯度震荡、训练不稳或策略学到回避长输出的劣策略（例如生成碎片化或提前停止）。
• 因此图 5 展示的现象本质上是：不合适地惩罚被截断样本，会降低训练质量（表现为验证准确率下降与熵异常）；而对截断样本进行过滤或采用平滑惩罚，会减少这种噪声，稳定训练并提高性能。

三、论文中采用的两种处理策略及其直觉（对应图中对比）

• Overlong Filtering（论文用到的第一个策略）：把被截断的样本"mask掉"，即在计算 policy loss 时不把这些样本纳入损失/优势计算中。实质上这是把"可疑/不可靠"的信号剔除，避免把误导信息用于更新。实现上对应伪代码：在计算 group 的 RiR_iRi 后，若样本 iii 被截断则 skip（或不给 loss）。但需配合 Dynamic Sampling，保证每个训练 batch 仍有足够的有效组。
• Soft Overlong Punishment（论文提出的更温和策略，公式在文中为式 (13)）：对超过阈值的长度给予一个"按超长程度线性/分段加重"的惩罚，而不是一刀切地负分或直接屏蔽。论文给出的形式为分段函数（我按论文排版写出）：
  Rlength(y)={0,∣y∣≤Lmax⁡−Lcache,Lmax⁡−Lcache−∣y∣Lcache,Lmax⁡−Lcache<∣y∣≤Lmax⁡−1,−1,∣y∣>Lmax⁡. R_{\text{length}}(y)= \begin{cases} 0, & |y| \le L_{\max}-L_{\text{cache}},\\[4pt] \dfrac{L_{\max}-L_{\text{cache}}-|y|}{L_{\text{cache}}}, & L_{\max}-L_{\text{cache}} < |y| \le L_{\max}-1,\\[6pt] -1, & |y| > L_{\max}. \end{cases} Rlength(y)=⎩ ⎨ ⎧0,LcacheLmax−Lcache−∣y∣,−1,∣y∣≤Lmax−Lcache,Lmax−Lcache<∣y∣≤Lmax−1,∣y∣>Lmax.
  （注：上面是论文给出的大意分段表达，实际实现可按论文细节调整）
• 直觉：在 ∣y∣|y|∣y∣ 接近但未超过 Lmax⁡L_{\max}Lmax 的区间，用一个逐渐增强的软惩罚告诉模型"你快要超限了，尽量短一点"；真正超过上限被截断时才给较重惩罚。这样能兼顾不鼓励无意义的无限拉长，又不把本来正确但微微超长的推理直接判为错误。

四、图 5 中性能与熵变化的解释（把现象和机制连起来）

• 精确信号减少噪声：Overlong Filtering 把那些因截断产生的"伪负样本"剔除，降低了组内 reward 的随机性，组内归一化（A^\hat AA^）因此更可靠，策略更新更稳定------这直接反映在 AIME 准确率的提升上（图 5(a)）。
• 熵的变化：当过滤掉被截断的"有问题"样本后，模型不再被误导去尝试极端多样/无意义的生成以规避长度惩罚，生成分布的熵因此更合理（图 5(b) 显示熵下降且更平滑）；反之若惩罚不合适，模型可能通过增长长度或变得更随机以探索规避手段，熵可异常升高。
• 两者的综合效果是训练更加稳定，模型更容易学到真正提高任务指标（如数学题正确率）的推理策略，而不是学习避开截断惩罚的表面技巧。

五、实现细节与工程建议（基于论文与常见实践）

• 如何判断"被截断"：在生成时记录实际生成 token 数 ∣y∣|y|∣y∣ 与最大允许长度 Lmax⁡L_{\max}Lmax，若生成被强制停止且 ∣y∣≥Lmax⁡|y|\ge L_{\max}∣y∣≥Lmax 则视为被截断。注意对于 streaming/pipeline 生成要在服务端协同判断。
• Overlong Filtering 的实现示例（伪代码）：
  • 在采样组 {oi}\{o_i\}{oi} 后，计算奖励 RiR_iRi 与是否截断标志 truncated_i。
  • 仅将满足 truncated_i == False 的样本加入用于计算组内均值/方差及 surrogate 的集合；若组内有效样本数太少，重采样或丢弃该组（Dynamic Sampling）。
• Soft Overlong Punishment 的参数选择：论文里给了一个实用设置（用于 Qwen-32B）------设置 Lmax⁡=16384L_{\max}=16384Lmax=16384，Lcache=4096L_{\text{cache}}=4096Lcache=4096（即最大生成设为 204802048020480，其中 163841638416384 是期望最大长度，额外 409640964096 作为软惩区间）。你可以根据任务调整比例与绝对值。
• 注意 Dynamic Sampling 的配合：Filtering 会降低每次采样的有效样本数，需用动态采样缓冲保证每个批次仍有足够的有效组，否则会牺牲训练效率或引入别的偏差。
• 数值/稳定性：对 reward 做归一和 σ\sigmaσ 下界（σ←max⁡(σ,ε)\sigma\leftarrow\max(\sigma,\varepsilon)σ←max(σ,ε)）仍然需要，即便做了过滤/soft punishment，也需避免方差为 0 或过小。

六、可做的消融实验与进一步研究方向（建议）

• 对比（A）hard filtering，（B）soft punishment，以及（C）不处理三种策略对最终性能、训练方差、熵和生成长度分布的影响。
• 在 soft punishment 中尝试不同的 penalty 曲线（线性、二次、sigmoid）并评估哪种对 long-CoT 更有利。
• 研究 learnable penalty：用小网络预测"截断惩罚"的尺度或直接训练一个 value 模型去估算"被截断时的真实回报"，以减少启发式门限对不同任务的敏感性。
• 分析 filtering 对样本多样性与过拟合的影响：剔除过长样本是否导致模型丧失学习复杂长链推理的机会？是否需要在后期逐步放宽过滤策略？

七、总结（一句话）

• 图 5 说明了：不恰当地惩罚被截断的过长生成会引入强噪声并破坏训练（表现为准确率下降和熵异常），而通过 Overlong Filtering 或 Soft Overlong Punishment 可以显著降低这种噪声，使训练更稳定并提升下游任务性能。

如果你想，我可以把 Overlong Filtering 与 Soft Overlong Punishment 的具体计算伪代码贴出来（包含如何在组内计算 RiR_iRi、如何标记截断、如何与 Dynamic Sampling 协同），或者帮你基于你自己的任务（告诉我典型生成长度/奖励范围）给出推荐的 Lmax⁡L_{\max}Lmax、LcacheL_{\text{cache}}Lcache 与 ε\varepsilonε 值。你想看哪一个？

好的，我来把公式 (13)（论文中用于 Overlong Reward Shaping 的分段惩罚函数）做一个完整、严格且易于实现的详解：公式、几何意义、为什么这么设计、数值例子、实现伪码、工程注意事项和可替代方案。含数学的句子我都用 LaTeX 表示。

1. 推荐的、易理解的分段形式（把论文中排版混乱的版本整理成对称且易实现的表达）：
   Rlength(y)={0,∣y∣≤Lmax⁡−Lcache,−∣y∣−(Lmax⁡−Lcache)Lcache,Lmax⁡−Lcache<∣y∣≤Lmax⁡,−1,∣y∣>Lmax⁡. R_{\text{length}}(y)= \begin{cases} 0, & |y| \le L_{\max}-L_{\text{cache}},\\[6pt] -\dfrac{|y|-(L_{\max}-L_{\text{cache}})}{L_{\text{cache}}}, & L_{\max}-L_{\text{cache}}<|y|\le L_{\max},\\[8pt] -1, & |y|>L_{\max}. \end{cases} Rlength(y)=⎩ ⎨ ⎧0,−Lcache∣y∣−(Lmax−Lcache),−1,∣y∣≤Lmax−Lcache,Lmax−Lcache<∣y∣≤Lmax,∣y∣>Lmax.

   解释：∣y∣|y|∣y∣ 表示生成的 token 数（response length）；Lmax⁡L_{\max}Lmax 是期望的"目标最大长度"；LcacheL_{\text{cache}}Lcache 是一个软惩罚区间的宽度（paper 中用作从 0 到 -1 的线性衰减区间）。

2. 该函数的直观含义与动机

• 当 ∣y∣≤Lmax⁡−Lcache|y|\le L_{\max}-L_{\text{cache}}∣y∣≤Lmax−Lcache 时，不施加长度惩罚，令 Rlength(y)=0R_{\text{length}}(y)=0Rlength(y)=0，即"在安全区间内不惩罚"。
• 当 Lmax⁡−Lcache<∣y∣≤Lmax⁡L_{\max}-L_{\text{cache}}<|y|\le L_{\max}Lmax−Lcache<∣y∣≤Lmax 时，按超出程度做线性惩罚，幅度从 000 线性减少到 −1-1−1，这相当于"告诉模型越靠近上限越不被鼓励，但给予平滑的梯度信号让模型逐步缩短"。
• 当 ∣y∣>Lmax⁡|y|>L_{\max}∣y∣>Lmax 时，给出固定的强惩罚 −1-1−1（或最大惩罚），表示严重超长/被截断的情况应强烈避免。
• 设计动机是避免"一刀切"的硬惩罚把正确但稍长的推理误判为坏样本，同时对明显过长或被截断的样本施以较强惩罚，从而减少 reward noise 并提供有意义的梯度信号。

3. 与原始正确性奖励的组合方式（实际训练中常见）

• 若原始规则奖励为 Rcorrect(y)∈{0,1}R_{\text{correct}}(y)\in\{0,1\}Rcorrect(y)∈{0,1}（正确为 1，错误为 0），则实际用于训练的总奖励常取为：
  Rtotal(y)=Rcorrect(y)+Rlength(y). R_{\text{total}}(y)=R_{\text{correct}}(y)+R_{\text{length}}(y). Rtotal(y)=Rcorrect(y)+Rlength(y).
• 这样当答案正确且长度正常时，Rtotal=1R_{\text{total}}=1Rtotal=1；当答案正确但接近上限或超出上限时，RtotalR_{\text{total}}Rtotal 会相应变小（甚至为负），从而让奖励既反映正确性又兼顾长度约束。

4. 具体数值示例（使用论文里的超参数示例）

• 论文训练细节里给的示例参数为 Lmax⁡=16384L_{\max}=16384Lmax=16384，Lcache=4096L_{\text{cache}}=4096Lcache=4096（于是允许最大生成为 Lmax⁡+Lcache=20480L_{\max}+L_{\text{cache}}=20480Lmax+Lcache=20480 但软惩区间从 122881228812288 到 163841638416384）：
  • 若 ∣y∣=12000|y|=12000∣y∣=12000，因为 12000≤1228812000\le 1228812000≤12288，所以 Rlength(y)=0R_{\text{length}}(y)=0Rlength(y)=0；若答案正确则 Rtotal=1R_{\text{total}}=1Rtotal=1。
  • 若 ∣y∣=13000|y|=13000∣y∣=13000，则
    Rlength(y)=−13000−122884096≈−7124096≈−0.174, R_{\text{length}}(y)=-\frac{13000-12288}{4096}\approx -\frac{712}{4096}\approx -0.174, Rlength(y)=−409613000−12288≈−4096712≈−0.174,
    若答案正确则 Rtotal≈0.826R_{\text{total}}\approx 0.826Rtotal≈0.826。
  • 若 ∣y∣=16384|y|=16384∣y∣=16384，则 Rlength(y)=−1R_{\text{length}}(y)=-1Rlength(y)=−1，若答案正确總賞為 000；若 ∣y∣>16384|y|>16384∣y∣>16384 同样 Rlength=−1R_{\text{length}}=-1Rlength=−1（严格超限时为最重惩罚）。

5. 为什么要用"线性软惩罚 + 硬阈值"而不是直接硬惩罚或完全过滤

• 线性软惩罚在 Lmax⁡−LcacheL_{\max}-L_{\text{cache}}Lmax−Lcache 到 Lmax⁡L_{\max}Lmax 之间提供平滑的梯度信号，有助于模型逐步学习缩短无益的冗余生成，而不是在一次训练步被强烈否定后出现剧烈策略摆动。
• 硬阈值（−1-1−1）用于明确区分"超限已导致截断/严重过长"的不可接受情形。
• 相比完全过滤（overlong filtering），soft punishment 在保留样本作为训练信号的同时以惩罚引导行为，能更高效利用数据；同时 filtering 与 soft punishment 可并用（paper 中先后提出两种策略并比较）。

6. 实现伪代码（把 R_length 与总 reward 结合并与 group-normalization 配合）
   注意：下列伪代码中含数学表达，已以 LaTeX 风格在行内/块内给出。

   伪代码：计算单个样本的 length penalty 与总 reward

   输入: response y, reference answer a,
   L_max, L_cache

   len_y = |y| # 生成的 token 数

   计算 length penalty R_length(y)

   if len_y <= L_max - L_cache:
   R_length = 0
   elif len_y <= L_max:
   R_length = - (len_y - (L_max - L_cache)) / L_cache
   else:
   R_length = -1

   计算 correctness reward R_correct（例如 1 或 0）

   R_correct = is_equivalent(a, y) ? 1 : 0

   总 reward

   R_total = R_correct + R_length

   将 R_total 用于组内归一化，计算 advantage:

   mu_R = mean({R_total_j}), sigma_R = std({R_total_j})

   A_hat_i = (R_total_i - mu_R) / max(sigma_R, eps)

7. 工程注意事项（避免数值/训练问题）

• 确保 ∣y∣|y|∣y∣ 的统计口径一致：使用相同 tokenizer 和计数方式（byte-pair / subword 等）。
• 在计算 σR\sigma_RσR 时要做下界处理：σR←max⁡(σR,ε)\sigma_R\leftarrow\max(\sigma_R,\varepsilon)σR←max(σR,ε) 以避免除零或极小方差导致优势爆炸。
• 如果许多样本被判为 ∣y∣>Lmax⁡|y|>L_{\max}∣y∣>Lmax（超限），则大量 Rlength=−1R_{\text{length}}=-1Rlength=−1 会导致组内 reward 分布偏低或方差小，需搭配 Dynamic Sampling 或过滤策略保证训练稳定。
• 是否把 RtotalR_{\text{total}}Rtotal 进一步 clip 到某个范围（例如 [−1,1][-1,1][−1,1]）可按实验决定，常见做法是保证 reward 在合理范围内以便训练超参数易调。
• 若任务中答案本身倾向较长的正确推理，Lmax⁡L_{\max}Lmax 与 LcacheL_{\text{cache}}Lcache 的选择需慎重；过小的 Lmax⁡L_{\max}Lmax 会把有用的长推理误判为过长。

8. 可替代/扩展的惩罚曲线（供研究或调参）

• 线性（当前）是最简单且可解释的。可以试以下变体：
  • 二次惩罚（惩罚随超长度平方增长）：Rlength(y)=−(∣y∣−(Lmax⁡−Lcache)Lcache)2R_{\text{length}}(y)=-\left(\frac{|y|-(L_{\max}-L_{\text{cache}})}{L_{\text{cache}}}\right)^2Rlength(y)=−(Lcache∣y∣−(Lmax−Lcache))2
  • Sigmoid/平滑饱和：Rlength(y)=−σ ⁣(α(∣y∣−(Lmax⁡−Lcache)))R_{\text{length}}(y)=-\sigma\!\Big(\alpha\big(|y|-(L_{\max}-L_{\text{cache}})\big)\Big)Rlength(y)=−σ(α(∣y∣−(Lmax−Lcache))) 并缩放到 [−1,0][-1,0][−1,0]，其中 α\alphaα 控制陡峭度。
  • Learnable penalty：训练一个小网络预测长度惩罚，以适配不同题型（需要额外的正则化以防学到 trivial 解）。
• 每种曲线对优化动态有不同影响：二次惩罚更强烈地抑制靠近上界的长度，sigmoid 则更平滑。

9. 选择 LcacheL_{\text{cache}}Lcache 的经验建议

• 论文使用 Lcache=4096L_{\text{cache}}=4096Lcache=4096 与 Lmax⁡=16384L_{\max}=16384Lmax=16384（即软惩区间占 Lmax⁡L_{\max}Lmax 的 25%25\%25%）。经验上 Lcache∈[0.1Lmax⁡, 0.3Lmax⁡]L_{\text{cache}}\in[0.1L_{\max},\,0.3L_{\max}]Lcache∈[0.1Lmax,0.3Lmax] 是一个合理起点，但具体任务需调参：若正确推理通常非常长，则应增大 LcacheL_{\text{cache}}Lcache 或提高 Lmax⁡L_{\max}Lmax；若希望严格控制长度，则减小 LcacheL_{\text{cache}}Lcache。

10. 总结要点（快速回顾）

• 公式 (13) 给出了一种"线性软惩罚 + 硬阈值"的长度惩罚函数，表达为：
  Rlength(y)={0,∣y∣≤Lmax⁡−Lcache,−∣y∣−(Lmax⁡−Lcache)Lcache,Lmax⁡−Lcache<∣y∣≤Lmax⁡,−1,∣y∣>Lmax⁡. R_{\text{length}}(y)= \begin{cases} 0, & |y| \le L_{\max}-L_{\text{cache}},\\[4pt] -\dfrac{|y|-(L_{\max}-L_{\text{cache}})}{L_{\text{cache}}}, & L_{\max}-L_{\text{cache}}<|y|\le L_{\max},\\[4pt] -1, & |y|>L_{\max}. \end{cases} Rlength(y)=⎩ ⎨ ⎧0,−Lcache∣y∣−(Lmax−Lcache),−1,∣y∣≤Lmax−Lcache,Lmax−Lcache<∣y∣≤Lmax,∣y∣>Lmax.
• 把它加到正确性奖励上（Rtotal=Rcorrect+RlengthR_{\text{total}}=R_{\text{correct}}+R_{\text{length}}Rtotal=Rcorrect+Rlength）可以平滑地惩罚过长生成，减少截断带来的 reward noise 并使训练更稳定，但需与归一化、下界 clipping、dynamic sampling 等策略配合使用。

如果你想，我可以：

• 给出一个具体的 NumPy/PyTorch 函数实现以便直接替换到你训练代码中；或
• 基于你手头任务的典型生成长度和 reward 范围，帮你推荐具体的 Lmax⁡L_{\max}Lmax、LcacheL_{\text{cache}}Lcache 与 ε\varepsilonε 设置，并预测可能的训练行为。你想要哪个？