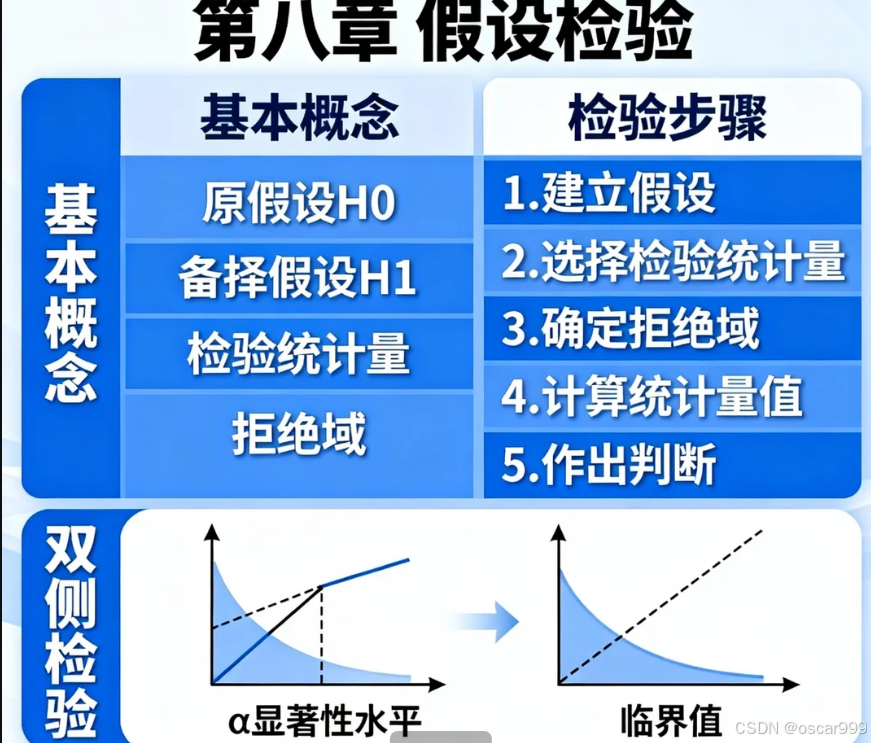
一、假设检验基本概念
1.1 基本定义
假设检验是根据样本信息对总体分布或参数提出假设,并利用样本信息判断假设是否成立的统计方法。
- 原假设 H0H_0H0:需要检验的假设,通常表示"无差异"或"无效果"
- 备择假设 H1H_1H1:与原假设对立的假设,通常表示"有差异"或"有效果"
- 检验统计量:用于判断是否拒绝原假设的样本统计量
- 显著性水平 α\alphaα:犯第一类错误(拒绝真原假设)的最大概率
- 拒绝域:导致拒绝原假设的检验统计量取值区域
- 临界点:拒绝域的边界值
1.2 假设检验的类型
双边检验 :
H0:θ=θ0,H1:θ≠θ0H_0: \theta = \theta_0, \quad H_1: \theta \neq \theta_0H0:θ=θ0,H1:θ=θ0
单边检验:
- 右侧检验:H0:θ≤θ0,H1:θ>θ0H_0: \theta \leq \theta_0, \quad H_1: \theta > \theta_0H0:θ≤θ0,H1:θ>θ0
- 左侧检验:H0:θ≥θ0,H1:θ<θ0H_0: \theta \geq \theta_0, \quad H_1: \theta < \theta_0H0:θ≥θ0,H1:θ<θ0
1.3 假设检验的步骤
- 提出原假设 H0H_0H0 和备择假设 H1H_1H1
- 确定检验统计量及其分布
- 给定显著性水平 α\alphaα,确定拒绝域
- 根据样本计算检验统计量的值
- 作出统计决策
例题 :某厂生产零件,标准长度为10cm,已知标准差为0.2cm。现抽取25个零件,测得平均长度为10.05cm。在显著性水平 α=0.05\alpha=0.05α=0.05 下,检验零件长度是否符合标准。
解:
- H0:μ=10H_0: \mu=10H0:μ=10,H1:μ≠10H_1: \mu\neq 10H1:μ=10
- 检验统计量:Z=Xˉ−μ0σ/n∼N(0,1)Z=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}\sim N(0,1)Z=σ/n Xˉ−μ0∼N(0,1)
- 拒绝域:∣Z∣>z0.025=1.96|Z|>z_{0.025}=1.96∣Z∣>z0.025=1.96
- 计算:Z=10.05−100.2/25=1.25Z=\frac{10.05-10}{0.2/\sqrt{25}}=1.25Z=0.2/25 10.05−10=1.25
- 决策:∣Z∣=1.25<1.96|Z|=1.25<1.96∣Z∣=1.25<1.96,不拒绝 H0H_0H0,认为零件长度符合标准
二、正态总体均值的假设检验
2.1 单个正态总体均值的检验
(1) 方差已知
检验统计量:
Z=Xˉ−μ0σ/n∼N(0,1)Z=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}\sim N(0,1)Z=σ/n Xˉ−μ0∼N(0,1)
拒绝域:
- 双边检验:∣Z∣>zα/2|Z|>z_{\alpha/2}∣Z∣>zα/2
- 右侧检验:Z>zαZ>z_\alphaZ>zα
- 左侧检验:Z<−zαZ<-z_\alphaZ<−zα
(2) 方差未知
检验统计量:
T=Xˉ−μ0S/n∼t(n−1)T=\frac{\bar{X}-\mu_0}{S/\sqrt{n}}\sim t(n-1)T=S/n Xˉ−μ0∼t(n−1)
拒绝域:
- 双边检验:∣T∣>tα/2(n−1)|T|>t_{\alpha/2}(n-1)∣T∣>tα/2(n−1)
- 右侧检验:T>tα(n−1)T>t_\alpha(n-1)T>tα(n−1)
- 左侧检验:T<−tα(n−1)T<-t_\alpha(n-1)T<−tα(n−1)
2.2 两个正态总体均值差的检验
(1) 方差已知
检验统计量:
Z=(Xˉ−Yˉ)−(μ1−μ2)σ12n1+σ22n2∼N(0,1)Z=\frac{(\bar{X}-\bar{Y})-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\sim N(0,1)Z=n1σ12+n2σ22 (Xˉ−Yˉ)−(μ1−μ2)∼N(0,1)
(2) 方差未知但相等
检验统计量:
T=(Xˉ−Yˉ)−(μ1−μ2)Sp1n1+1n2∼t(n1+n2−2)T=\frac{(\bar{X}-\bar{Y})-(\mu_1-\mu_2)}{S_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\sim t(n_1+n_2-2)T=Spn11+n21 (Xˉ−Yˉ)−(μ1−μ2)∼t(n1+n2−2)
其中合并方差:
Sp2=(n1−1)S12+(n2−1)S22n1+n2−2S_p^2=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}Sp2=n1+n2−2(n1−1)S12+(n2−1)S22
(3) 方差未知且不等
检验统计量:
T=(Xˉ−Yˉ)−(μ1−μ2)S12n1+S22n2∼t(df)T=\frac{(\bar{X}-\bar{Y})-(\mu_1-\mu_2)}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}\sim t(df)T=n1S12+n2S22 (Xˉ−Yˉ)−(μ1−μ2)∼t(df)
其中自由度:
df=(S12n1+S22n2)2(S12/n1)2n1−1+(S22/n2)2n2−1df=\frac{\left(\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}\right)^2}{\frac{(S_1^2/n_1)^2}{n_1-1}+\frac{(S_2^2/n_2)^2}{n_2-1}}df=n1−1(S12/n1)2+n2−1(S22/n2)2(n1S12+n2S22)2
2.3 逐对比较法(基于成对数据的检验)
当两个样本是成对数据时,设 Di=Xi−YiD_i=X_i-Y_iDi=Xi−Yi,则 D1,...,DnD_1,\ldots,D_nD1,...,Dn 来自正态总体 N(μD,σD2)N(\mu_D,\sigma_D^2)N(μD,σD2)
检验统计量:
T=Dˉ−μD0SD/n∼t(n−1)T=\frac{\bar{D}-\mu_{D0}}{S_D/\sqrt{n}}\sim t(n-1)T=SD/n Dˉ−μD0∼t(n−1)
例题:为比较两种教学方法,选取10对学生,每对学生的初始成绩相近,分别用两种方法教学,成绩如下:
| 学生对 | 方法A | 方法B | 差值D |
|---|---|---|---|
| 1 | 85 | 82 | 3 |
| 2 | 78 | 75 | 3 |
| ... | ... | ... | ... |
| 10 | 88 | 85 | 3 |
计算得 Dˉ=2.5\bar{D}=2.5Dˉ=2.5,SD=1.2S_D=1.2SD=1.2。检验两种方法是否有显著差异 (α=0.05\alpha=0.05α=0.05)。
解:
- H0:μD=0H_0: \mu_D=0H0:μD=0,H1:μD≠0H_1: \mu_D\neq 0H1:μD=0
- 检验统计量:T=2.5−01.2/10=6.58T=\frac{2.5-0}{1.2/\sqrt{10}}=6.58T=1.2/10 2.5−0=6.58
- 拒绝域:∣T∣>t0.025(9)=2.262|T|>t_{0.025}(9)=2.262∣T∣>t0.025(9)=2.262
- 决策:6.58>2.2626.58>2.2626.58>2.262,拒绝 H0H_0H0,两种教学方法有显著差异
三、正态总体方差的假设检验
3.1 单个总体方差的检验
检验统计量:
χ2=(n−1)S2σ02∼χ2(n−1)\chi^2=\frac{(n-1)S^2}{\sigma_0^2}\sim \chi^2(n-1)χ2=σ02(n−1)S2∼χ2(n−1)
拒绝域:
- 双边检验:χ2<χ1−α/22(n−1)\chi^2<\chi^2_{1-\alpha/2}(n-1)χ2<χ1−α/22(n−1) 或 χ2>χα/22(n−1)\chi^2>\chi^2_{\alpha/2}(n-1)χ2>χα/22(n−1)
- 右侧检验:χ2>χα2(n−1)\chi^2>\chi^2_\alpha(n-1)χ2>χα2(n−1)
- 左侧检验:χ2<χ1−α2(n−1)\chi^2<\chi^2_{1-\alpha}(n-1)χ2<χ1−α2(n−1)
3.2 两个总体方差的检验
检验统计量:
F=S12S22∼F(n1−1,n2−1)F=\frac{S_1^2}{S_2^2}\sim F(n_1-1,n_2-1)F=S22S12∼F(n1−1,n2−1)
拒绝域:
- 双边检验:F<F1−α/2(n1−1,n2−1)F<F_{1-\alpha/2}(n_1-1,n_2-1)F<F1−α/2(n1−1,n2−1) 或 F>Fα/2(n1−1,n2−1)F>F_{\alpha/2}(n_1-1,n_2-1)F>Fα/2(n1−1,n2−1)
- 右侧检验:F>Fα(n1−1,n2−1)F>F_\alpha(n_1-1,n_2-1)F>Fα(n1−1,n2−1)
- 左侧检验:F<F1−α(n1−1,n2−1)F<F_{1-\alpha}(n_1-1,n_2-1)F<F1−α(n1−1,n2−1)
例题 :两台机床加工零件,从甲机床产品中抽取8件,测得方差 S12=0.095S_1^2=0.095S12=0.095;从乙机床产品中抽取10件,测得方差 S22=0.063S_2^2=0.063S22=0.063。检验两机床精度是否有显著差异 (α=0.1\alpha=0.1α=0.1)。
解:
- H0:σ12=σ22H_0: \sigma_1^2=\sigma_2^2H0:σ12=σ22,H1:σ12≠σ22H_1: \sigma_1^2\neq\sigma_2^2H1:σ12=σ22
- 检验统计量:F=0.0950.063=1.508F=\frac{0.095}{0.063}=1.508F=0.0630.095=1.508
- 拒绝域:F<F0.95(7,9)=1F0.05(9,7)=13.68=0.272F<F_{0.95}(7,9)=\frac{1}{F_{0.05}(9,7)}=\frac{1}{3.68}=0.272F<F0.95(7,9)=F0.05(9,7)1=3.681=0.272 或 F>F0.05(7,9)=3.29F>F_{0.05}(7,9)=3.29F>F0.05(7,9)=3.29
- 决策:0.272<1.508<3.290.272<1.508<3.290.272<1.508<3.29,不拒绝 H0H_0H0,认为两机床精度无显著差异
四、分布拟合检验
4.1 单个分布的 χ2\chi^2χ2 拟合检验法
步骤:
- 将总体 XXX 的取值范围分成 kkk 个互不相交的区间 A1,...,AkA_1,\ldots,A_kA1,...,Ak
- 计算每个区间的观测频数 fif_ifi
- 根据假设分布计算每个区间的期望频数 npinp_inpi
- 计算检验统计量:
χ2=∑i=1k(fi−npi)2npi∼χ2(k−r−1)\chi^2=\sum_{i=1}^k\frac{(f_i-np_i)^2}{np_i}\sim \chi^2(k-r-1)χ2=i=1∑knpi(fi−npi)2∼χ2(k−r−1) - 其中 rrr 是估计的参数个数
- 拒绝域:χ2>χα2(k−r−1)\chi^2>\chi^2_\alpha(k-r-1)χ2>χα2(k−r−1)
4.2 分布族的 χ2\chi^2χ2 拟合检验方法
当分布族中含有未知参数时,先用极大似然法估计参数,再进行拟合检验。
例题:检验某批产品寿命是否服从指数分布。抽取100件产品进行寿命试验,结果分组如下:
| 寿命区间(小时) | 观测频数 |
|---|---|
| 0-100 | 35 |
| 100-200 | 25 |
| 200-300 | 18 |
| 300-400 | 12 |
| 400以上 | 10 |
解:
- 假设 H0H_0H0:寿命服从指数分布 f(x)=λe−λxf(x)=\lambda e^{-\lambda x}f(x)=λe−λx,x>0x>0x>0
- 用样本均值估计 λ\lambdaλ:λ^=1/xˉ\hat{\lambda}=1/\bar{x}λ^=1/xˉ
- 计算每个区间的概率:pi=F(ai)−F(ai−1)p_i=F(a_i)-F(a_{i-1})pi=F(ai)−F(ai−1)
- 计算期望频数 npinp_inpi
- 计算检验统计量 χ2\chi^2χ2
- 与临界值比较作出决策
历年考题分析
2018年考题 :设 X1,...,XnX_1,\ldots,X_nX1,...,Xn 是来自正态总体 N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2) 的样本,σ2\sigma^2σ2 未知。考虑检验问题 H0:μ=μ0H_0:\mu=\mu_0H0:μ=μ0 vs H1:μ≠μ0H_1:\mu\neq\mu_0H1:μ=μ0。给出检验统计量和拒绝域,并说明检验的原理。
解:
- 检验统计量:T=Xˉ−μ0S/n∼t(n−1)T=\frac{\bar{X}-\mu_0}{S/\sqrt{n}}\sim t(n-1)T=S/n Xˉ−μ0∼t(n−1)
- 拒绝域:∣T∣>tα/2(n−1)|T|>t_{\alpha/2}(n-1)∣T∣>tα/2(n−1)
- 原理:根据小概率原理,在原假设成立时,检验统计量落入拒绝域的概率很小 (α\alphaα)。如果一次抽样中统计量落入拒绝域,则有理由怀疑原假设不真。
2019年考题:为比较两种降血压药的疗效,将20名高血压患者随机分成两组,每组10人,分别服用A药和B药。测得降压值如下:
- A药:12, 15, 10, 13, 16, 14, 11, 17, 12, 15
- B药:14, 16, 13, 15, 18, 12, 14, 17, 15, 16
假设降压值服从正态分布且方差相等,检验两种药的降压效果是否有显著差异 (α=0.05\alpha=0.05α=0.05)。
解:
- H0:μA=μBH_0: \mu_A=\mu_BH0:μA=μB,H1:μA≠μBH_1: \mu_A\neq\mu_BH1:μA=μB
- 计算:XˉA=13.5\bar{X}_A=13.5XˉA=13.5,XˉB=15.0\bar{X}_B=15.0XˉB=15.0,SA2=4.72S_A^2=4.72SA2=4.72,SB2=3.33S_B^2=3.33SB2=3.33
- 合并方差:Sp2=9×4.72+9×3.3318=4.025S_p^2=\frac{9\times4.72+9\times3.33}{18}=4.025Sp2=189×4.72+9×3.33=4.025
- 检验统计量:T=13.5−15.04.025×(110+110)=−1.67T=\frac{13.5-15.0}{\sqrt{4.025\times(\frac{1}{10}+\frac{1}{10})}}=-1.67T=4.025×(101+101) 13.5−15.0=−1.67
- 临界值:t0.025(18)=2.101t_{0.025}(18)=2.101t0.025(18)=2.101
- 决策:∣T∣=1.67<2.101|T|=1.67<2.101∣T∣=1.67<2.101,不拒绝 H0H_0H0,认为两种药降压效果无显著差异