用栈模拟递归：以快速排序为例，告别栈溢出烦恼

在写代码时，递归常常能让复杂问题变简单 ------ 比如快速排序、二叉树遍历，几行代码就能搞定。但递归也有个大痛点：栈溢出。今天就聊聊为什么会栈溢出，以及如何用「栈」模拟递归实现快速排序，彻底解决这个问题。

一、递归的 "坑"：为什么会栈溢出？

先简单理解下递归的底层逻辑：当函数递归调用时，每次调用都会在内存的「栈区」创建一个 "临时工作区"（称为栈帧），用来存放函数的参数、局部变量和返回地址。等函数执行完，这个栈帧才会被销毁。

但「栈区」的空间很小（通常只有几 MB），如果递归次数太多（比如排序 10 万条数据，递归深度可能达到几万层），栈区就会被栈帧占满，直接触发「栈溢出」错误。

那有没有办法避开这个坑？当然有！我们可以自己用代码实现一个「栈」，把递归需要的参数（比如快排的区间边界）存到这个栈里。关键是：我们自己创建的栈，是向内存的「堆区」申请空间的，而堆区空间很大（通常是 GB 级），根本不用担心溢出。

二、先打基础：快速排序的递归实现

在讲栈模拟前，得先搞懂快排的递归逻辑 ------ 核心就是 "分而治之"，步骤很简单：

1. 选一个「基准值」（比如区间第一个元素）；
2. 把区间里比基准小的数放左边，比基准大的放右边（一趟排序）；
3. 对左边和右边的子区间，重复步骤 1-2，直到子区间只有 1 个元素（递归终止）。

2.1 递归实现的 2 个优化（避免深度过大）

直接递归容易出问题，所以我们加两个优化：

• 三数取中：选区间左、中、右三个位置的中间值当基准，避免选到最大 / 最小值（否则子区间会一边大一边小，递归深度暴增）；
• 小区间用插入排序：当区间长度小于 10 时，改用插入排序（小数据量下，插入排序比快排效率高，还能减少递归次数）。

2.2 快速排序递归核心代码

c

#include <stdio.h>
// 交换两个元素（辅助函数）
void Swap(int* x, int* y) {
    int tmp = *x;
    *x = *y;
    *y = tmp;
}

// 1. 三数取中：找到左、中、右三个位置的中间值下标
int middle(int* a, int left, int right) {
    int mid = (left + right) / 2;
    // 判断三个数的大小关系，返回中间值的下标
    if ((a[left] <= a[mid] && a[right] >= a[mid]) || (a[right] <= a[mid] && a[left] >= a[mid])) {
        return mid;
    } else if ((a[mid] <= a[left] && a[right] >= a[left]) || (a[right] <= a[left] && a[mid] >= a[left])) {
        return left;
    } else {
        return right;
    }
}

// 2. 一趟排序：把区间按基准分成左右两部分，返回基准下标
int PartSort1(int* a, int left, int right) {
    // 三数取中优化：把中间值换到左边界（基准默认左边界）
    int mid = middle(a, left, right);
    Swap(&a[mid], &a[left]);
    
    int keyi = left;  // 基准下标（初始为左边界）
    int begin = left; // 左指针
    int end = right;  // 右指针

    // 左右指针向中间靠拢，交换不符合条件的元素
    while (begin < end) {
        // 右指针找比基准小的元素
        while (begin < end && a[end] >= a[keyi]) {
            end--;
        }
        // 左指针找比基准大的元素
        while (begin < end && a[begin] <= a[keyi]) {
            begin++;
        }
        // 交换左右指针找到的元素
        Swap(&a[begin], &a[end]);
    }
    // 基准归位：把基准换到左右指针相遇的位置
    Swap(&a[keyi], &a[begin]);
    keyi = begin; // 更新基准下标
    return keyi;
}

// 3. 插入排序（小区间优化用）
void InsertSort(int* a, int n) {
    for (int i = 1; i < n; i++) {
        int tmp = a[i];
        int j = i - 1;
        // 找插入位置
        while (j >= 0 && a[j] > tmp) {
            a[j + 1] = a[j];
            j--;
        }
        a[j + 1] = tmp;
    }
}

// 4. 快速排序递归实现
void QuickSort(int* a, int left, int right) {
    // 递归终止条件：区间为空或只有1个元素
    if (left >= right) {
        return;
    }
    // 小区间优化：长度<10时用插入排序
    if (right - left + 1 < 10) {
        InsertSort(a + left, right - left + 1);
    } else {
        // 一趟排序找基准，分左右子区间
        int keyi = PartSort1(a, left, right);
        // 递归处理左子区间 [left, keyi-1]
        QuickSort(a, left, keyi - 1);
        // 递归处理右子区间 [keyi+1, right]
        QuickSort(a, keyi + 1, right);
    }
}

三、重点：用栈模拟快排递归

递归的核心是「不断拆分区间，处理子区间」，而栈的「先进后出」特性刚好能模拟这个过程 ------ 我们用栈来存待处理的区间（左、右边界），代替递归的 "函数调用栈"。

3.1 核心思路：栈如何模拟递归？

递归是 "先处理左子区间，再处理右子区间"，栈要实现这个顺序，需要注意入栈顺序：因为栈是 "先进后出"，所以要「先压右子区间，再压左子区间」------ 这样出栈时会先取到左子区间，和递归的处理顺序完全一致。

具体步骤：

1. 初始化栈，把初始区间的「右边界」和「左边界」压入栈（注意：先压右，再压左，因为栈取的时候是反的）；
2. 循环：只要栈不为空，就出栈获取当前要处理的区间（先出左边界，再出右边界）；
3. 对当前区间做一趟排序，找到基准下标keyi；
4. 判断右子区间[keyi+1, end]是否需要处理（如果keyi+1 < end，说明有至少 2 个元素），需要则压栈；
5. 判断左子区间[begin, keyi-1]是否需要处理（如果keyi-1 > begin），需要则压栈；
6. 重复步骤 2-5，直到栈空，排序完成。

3.2 快速排序非递归（栈模拟）代码

首先，我们需要一个基础的栈结构（存 int 类型，因为要存区间边界），这里假设已经实现了栈的头文件stack.h（文末会附栈的核心接口）。

c

#include "stack.h"  // 包含栈的基本操作（Init、Push、Pop等）
#include <stdio.h>

// 快速排序非递归实现（栈模拟）
void QuickSortNonR(int* a, int left, int right) {
    // 1. 初始化栈
    ST st_sort;  // ST是栈的结构体类型（定义在stack.h中）
    STInit(&st_sort);

    // 2. 压入初始区间：先压右边界，再压左边界
    STPush(&st_sort, right);
    STPush(&st_sort, left);

    // 3. 循环处理栈中的区间，直到栈空
    while (!STEmpty(&st_sort)) {
        // 出栈：先取左边界，再取右边界（和入栈顺序相反）
        int begin = STTop(&st_sort);  // 取左边界
        STPop(&st_sort);              // 弹出左边界
        int end = STTop(&st_sort);    // 取右边界
        STPop(&st_sort);              // 弹出右边界

        // 4. 一趟排序，找基准下标（和递归实现用同一个函数，复用优化）
        int keyi = PartSort1(a, begin, end);

        // 5. 处理右子区间 [keyi+1, end]：满足条件才压栈（避免空区间）
        if (keyi + 1 < end) {
            STPush(&st_sort, end);    // 先压右边界
            STPush(&st_sort, keyi + 1);// 再压左边界
        }

        // 6. 处理左子区间 [begin, keyi-1]：满足条件才压栈
        if (keyi - 1 > begin) {
            STPush(&st_sort, keyi - 1);// 先压右边界
            STPush(&st_sort, begin);   // 再压左边界
        }
    }

    // 7. 销毁栈，释放内存（避免内存泄漏）
    STDestroy(&st_sort);
}

3.3 关键细节解释

• 为什么要判断keyi+1 < end才压栈？这对应递归的终止条件left >= right------ 如果keyi+1 >= end，说明右子区间只有 1 个元素或为空，不需要处理，直接跳过（不压栈）。
• 栈里存的是 "区间边界"，不是整个数组？是的！这样更节省空间 ------ 我们只需要知道要处理的范围，数组本身是全局 / 传参的，不需要重复存储。

四、图文辅助：直观理解递归与栈模拟

文字不够直观，建议配 2 张图，帮你快速搞懂核心逻辑。

图 1：快速排序递归调用树状图

以数组[3,1,4,1,5,9]（初始区间[0,5]）为例，递归调用的过程像一棵 "拆分树"：

plaintext

          初始区间 [0,5]
             ↓（找基准后分左右）
    [0,2]（左子区间）    [4,5]（右子区间）
       ↓                    ↓
[0,1]（左）  [无]（右）  [无]（左）  [无]（右）
   ↓
[无] [1,1]（右）

每一层都是 "拆分区间→处理子区间"，直到子区间为空或只有 1 个元素。

图 2：栈模拟过程示意图

还是以初始区间[0,5]为例，栈的入栈、出栈过程如下（栈底→栈顶）：

步骤	栈内元素（右边界，左边界）	操作说明
1	[5, 0]	初始化，压入初始区间（先压 5，再压 0）
2	空	出栈 0、5，处理区间 [0,5]，找基准 keyi=2
3	[5,4, 2,0]	压右子区间 [4,5]（5,4），再压左子区间 [0,2]（2,0）
4	[5,4]	出栈 0、2，处理区间 [0,2]，找基准 keyi=1
5	[5,4, 0,0]	右子区间 [2,2]（不满足条件，不压），压左子区间 [0,0]（不满足？假设 keyi=1，左区间 [0,0]，keyi-1=0 > begin=0？不，0 不大于 0，所以不压？这里根据实际基准调整，核心是 "满足条件才压"）
6	[5,4]	栈内只剩 [5,4]，出栈 4、5，处理区间 [4,5]
7	空	处理 [4,5] 后，子区间不满足条件，不压栈
8	空	栈空，排序完成

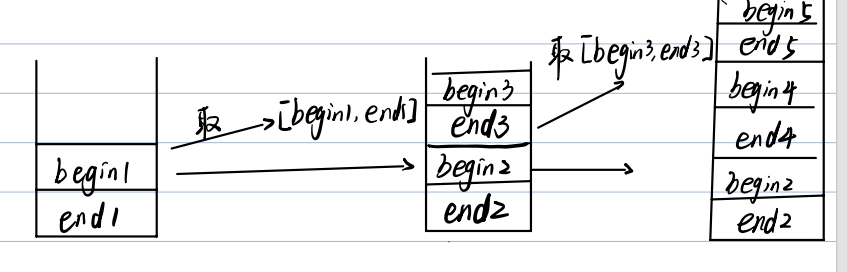
通过这张图，能清晰看到栈如何 "代替递归"，一步步处理所有子区间。

五、补充：栈的基础实现（stack.h）

前面的代码用到了栈的操作，这里给出stack.h的核心接口和实现，方便你直接用：

// stack.h（栈的头文件）
#ifndef __STACK_H__
#define __STACK_H__

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

// 栈的结构体（存int类型，用于存区间边界）
typedef struct Stack {
    int* data;   // 数据数组
    int top;     // 栈顶指针（指向栈顶元素的下一个位置）
    int capacity;// 栈的容量
} ST;

// 栈的基本操作
void STInit(ST* pst);         // 初始化栈
void STDestroy(ST* pst);      // 销毁栈
void STPush(ST* pst, int x);  // 压栈
void STPop(ST* pst);          // 出栈
int STTop(ST* pst);           // 获取栈顶元素
int STEmpty(ST* pst);         // 判断栈是否为空

#endif // __STACK_H__

// stack.c（栈的实现）
#include "stack.h"

// 初始化栈
void STInit(ST* pst) {
    assert(pst);
    pst->data = NULL;
    pst->top = 0;
    pst->capacity = 0;
}

// 销毁栈
void STDestroy(ST* pst) {
    assert(pst);
    free(pst->data);
    pst->data = NULL;
    pst->top = pst->capacity = 0;
}

// 压栈（扩容）
void STPush(ST* pst, int x) {
    assert(pst);
    // 扩容：初始容量为4，满了就翻倍
    if (pst->top == pst->capacity) {
        int newCap = (pst->capacity == 0) ? 4 : pst->capacity * 2;
        int* tmp = (int*)realloc(pst->data, newCap * sizeof(int));
        if (tmp == NULL) {
            perror("realloc fail");
            exit(1);
        }
        pst->data = tmp;
        pst->capacity = newCap;
    }
    // 压入元素
    pst->data[pst->top++] = x;
}

// 出栈（栈不为空）
void STPop(ST* pst) {
    assert(pst);
    assert(!STEmpty(pst));
    pst->top--;
}

// 获取栈顶元素（栈不为空）
int STTop(ST* pst) {
    assert(pst);
    assert(!STEmpty(pst));
    return pst->data[pst->top - 1];
}

// 判断栈是否为空：空返回1，非空返回0
int STEmpty(ST* pst) {
    assert(pst);
    return pst->top == 0;
}

六、总结：用栈模拟递归的好处与拓展

1. 避免栈溢出：自己实现的栈用堆区空间，比系统栈大得多，适合处理大数据量；
2. 逻辑可控：递归的调用栈是系统自动管理的，栈模拟则可以手动控制入栈、出栈，方便调试；
3. 通用性强：不只是快速排序，其他递归算法（比如二叉树的前 / 中 / 后序遍历、归并排序）都能用栈模拟。

下次再遇到递归栈溢出的问题，不妨试试用栈来 "手动管理" 递归过程，简单又高效！