本文是记录专业课计算机图形学的部分笔记,参考教材为Angel的第八版交互式计算机图形学------基于WebGL 2.0的自顶向下方法。
1、现在我们来考虑多边形裁剪,这就不像线段裁剪那样简单了。裁剪一条线段最多得到一条线段,但裁剪一个多边形可以得到多个多边形------除非是凸多边形,裁剪凸多边形最多得到一个多边形!因此一种方法就是把非凸多边形用一组三角形代替,这个过程称为划分(tessellation),这同样也使得填充变得简单,且在GLU库中有划分代码,但最好的方法就是由用户自己进行。
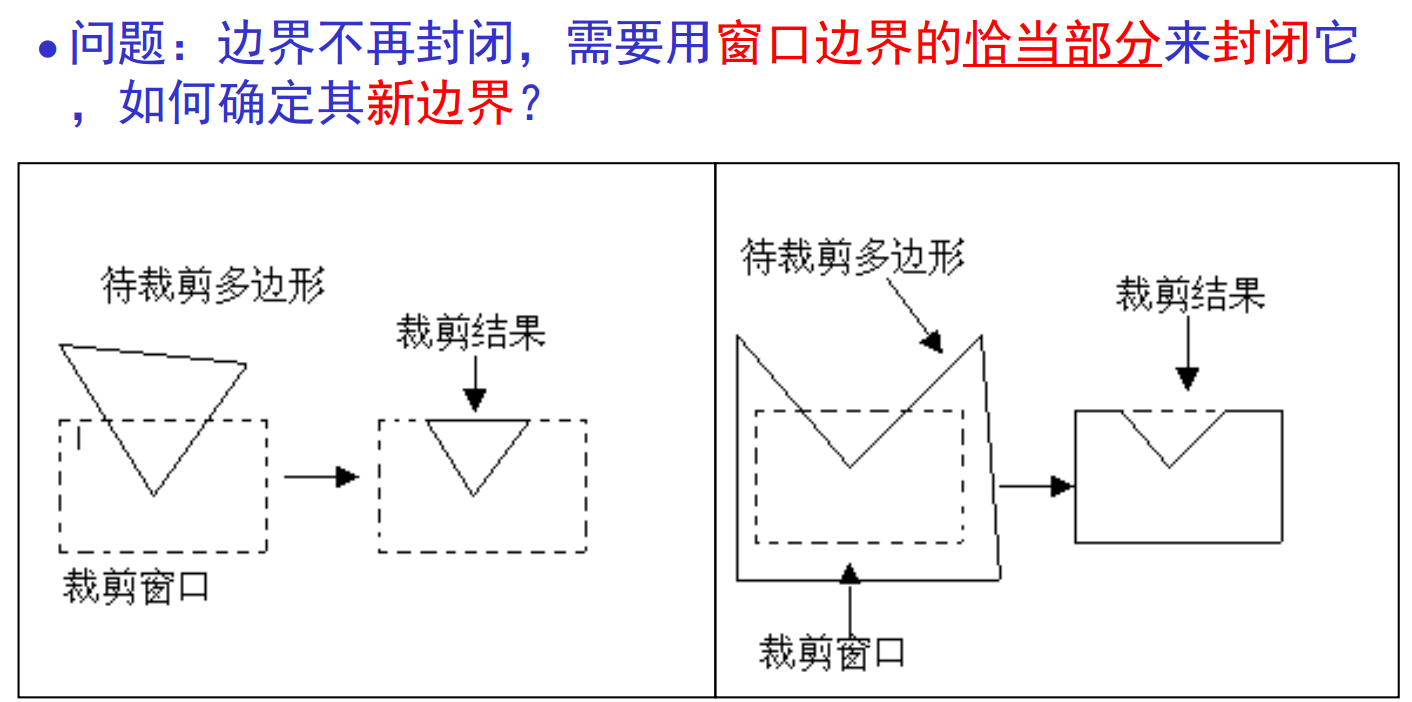
2、裁剪器(Clipper)是一个黑盒,可以认为线段的裁剪就是从两个顶点出发,得到的结果为:没有/删除顶点(外部被删除) 或者裁剪后线段的2个顶点(内部被保留)。线段裁剪的流水线体系如下图所示,多边形也差不多,每个面是分开的(三维的话增加前与后裁剪器,SGI Geometry Engine中应用这种策略,在延迟方面有很小增长,体现效率)。
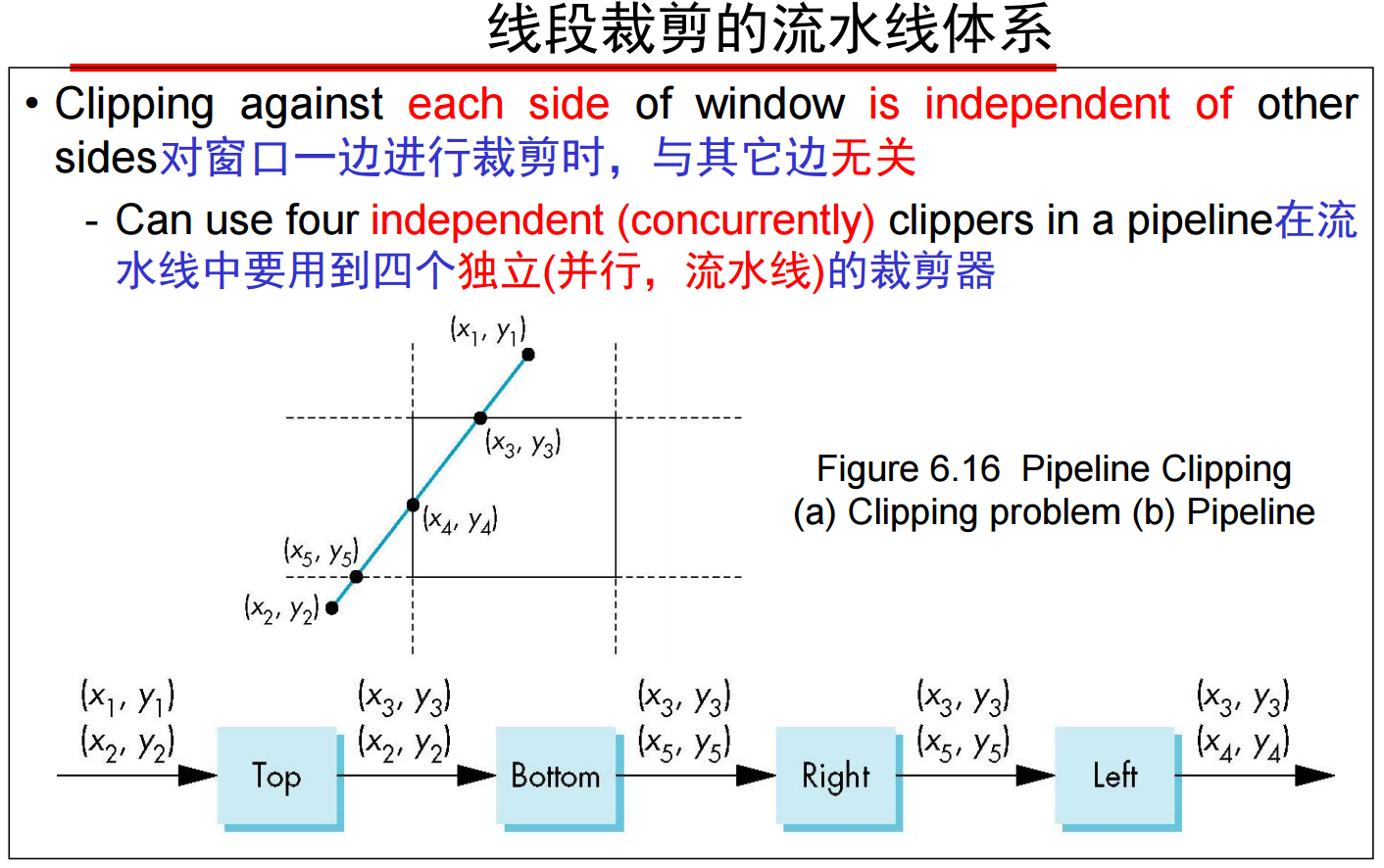
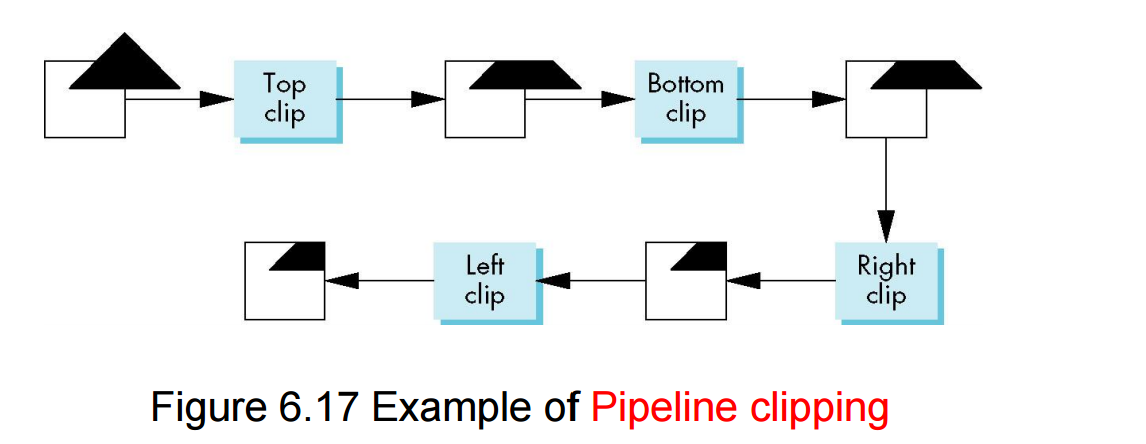
3、Sutherland-Hodgeman算法,既是多边形裁剪的过程,又是多边形重构的过程:
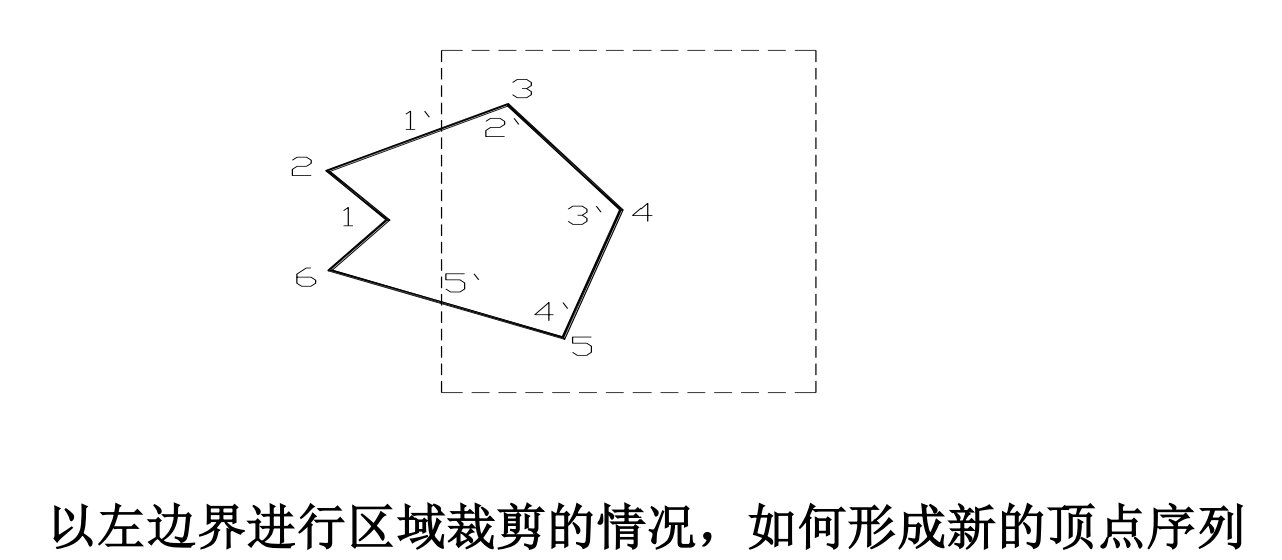
对凸多边形应用本算法可以得到正确的结果,但是对凹多边形的裁剪则会显示出一条多余的直线。这种情况在裁剪后的多边形有两个或者多个分离部分的时候出现。因为只有一个输出顶点表,所以表中最后一个顶点总是连着第一个顶点。解决这个问题有多种方法,一是把凹多边形分割成若干个凸多边形,然后分别处理各个凸多边形;二是修改本算法,沿着任何一个裁剪窗口边检查顶点表,正确的连接顶点对。再有就是Weiler-Atherton算法(见第23讲)。
4、一种更清晰的方案是包围盒(Bounding Boxes),不是直接对复杂多边形进行裁剪,而是先用一个方向与坐标轴平行的长方体或其它形状包围多边形(包围盒应尽可能地小、误差小,容易计算出坐标的最大最小值、计算量小),然后直接基于包围盒确定多边形的完全接受与完全拒绝:

5、我们注意到,裁剪和隐藏面消除有许多共同点------都是希望把看不到的对象从视野中去掉。我们可以通过在处理过程中提早应用可见性或者遮挡检测(visibility or occlusion testing),从而在进入流水线体系之前消去尽可能多的多边形。这一步在流水线的位置是什么?在顶点经过几何变后,其所定义的几何对象经过了装配与裁剪(得到的是一组点、线段和多边形,在最终的投影后,其中所有的几何对象都有可能出现在显示设备上),此时需要进行隐藏面消除------这有两种方法:
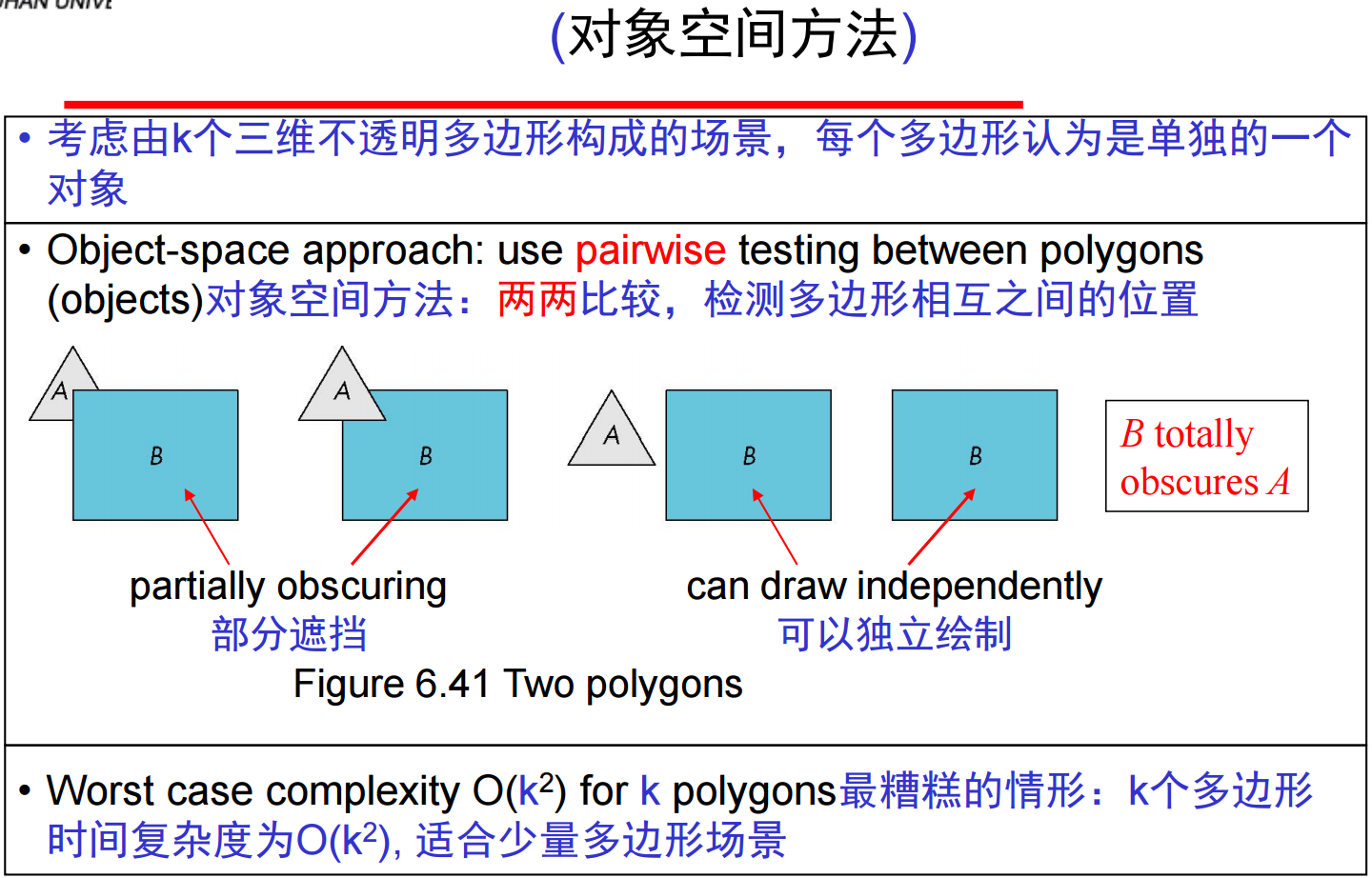
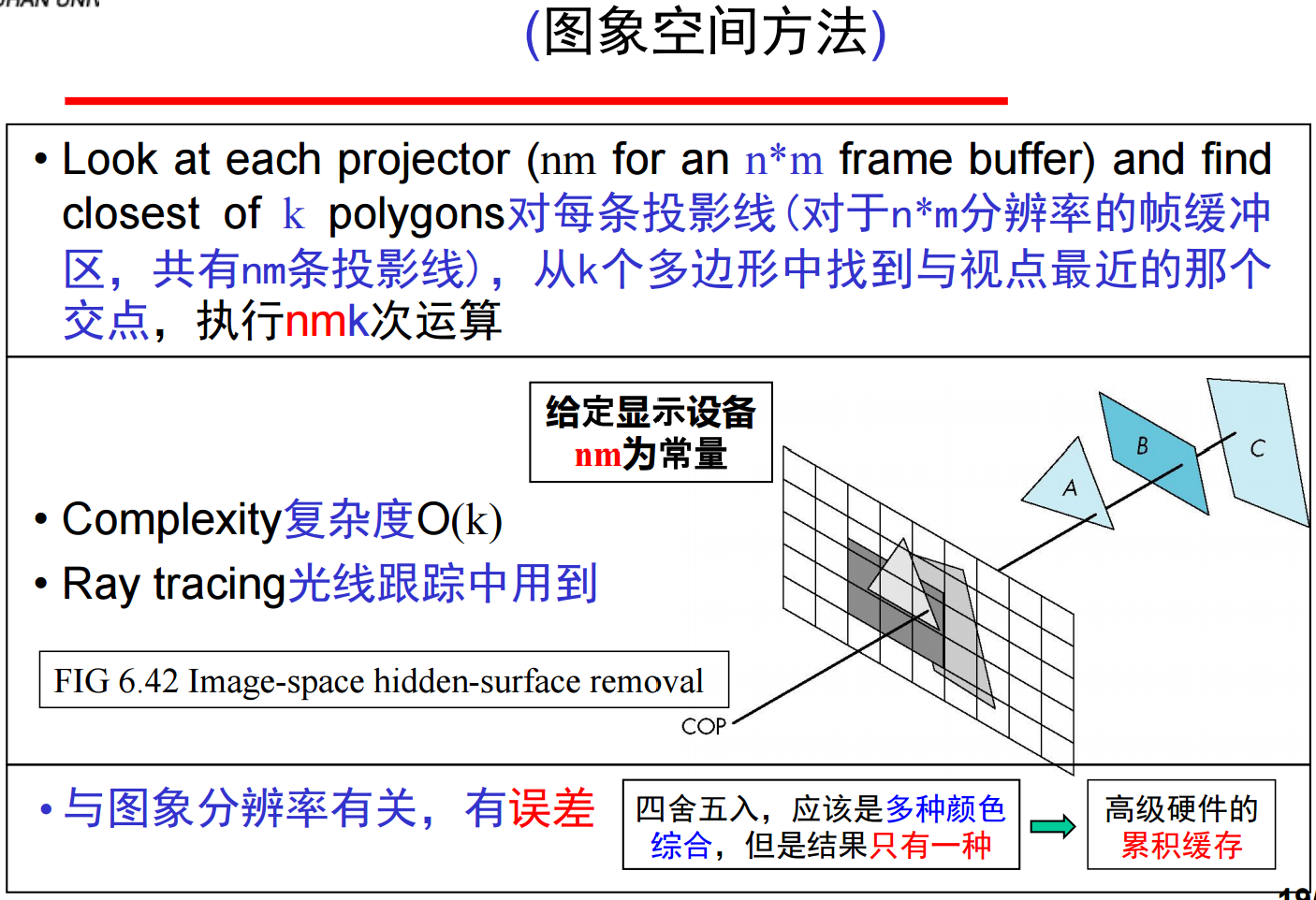
具体的对象空间方法有画家算法与深度排序、背面剔除;图像空间算法有z缓冲区算法。以Z-buffer算法为代表的图象空间方法(实际是混合方法),在底层图形硬件pipeline系统中广泛应用。但是,高层的可视化系统图形系统和应用程序中,通过对象空间方法,可以减少发送到硬件系统的多边形的数量。
6、接下来我们来考虑画家算法与深度排序(Painter's Algorithm and Depth Sort):假设场景内的多边形已按离观察者的距离排序,那么按从后到前的顺序把每个多边形完全绘制出来即可。

简单情形有两种:①多边形A位于所有其它多边形后面(见上图),那么可以先绘制出来。②多边
形在z方向有重叠,但在x或y方向没有重叠,则可以分别绘制出来:



具体算法:
Step 1:将场景中所有多边形存入一个线性表(链表或数组),记为 L。
Step 2:如果 L中仅有一个多边形,算法结束;否则根据每个多边形的 nmin对它们预排序。不妨假定多边形 P落在表首,即 nmin(P)为最小。再记 Q为 L -- {P}(表中其余多边形)中任意一个。
Step 3:判别 P,Q之间的关系,有如下二种:
step 3.1:对有的 Q,有 nmax(P)< nmin (Q),则多边形的确距观察点最远,它不可能遮挡别的多边形。令 L = L -- {P},返回 step 2。
step 3.2:存在某一个多边形 Q,使 nmax(P) > nmin (Q),则需进一步判别。
step 3.2.1:若 P,Q投影 P', Q'的包围盒不相交,则 P,Q在表中的次序不重要,令 L = L -- {P}, 返回 step 2。否则进行下一步。
step 3.2.2:若 P的所有顶点位于Q所在平面的不可见的一侧,则 P,Q关系正确,令 L = L -- {P},返回 step 2。否则进行下一步。
step 3.2.3:若 Q 的所有顶点位于 P所在平面的可见的一侧,则 P,Q关系正确,令 L = L -- {P}, 返回 step 2。否则进行下一步。
step 3.2.4:对 P,Q投影 P',Q'求交判断,若 P',Q'不相交,则 P,Q在表中的次序不重要,令 L = L -- {P},返回 step 。否则在它们所相交的区域中任取一点,计算P,Q在该点的深度值,如果 P的深度小,则 P,Q关系正确,令 L = L -- {P}, 返回step 2; 否则交换 P,Q, 返回 step 3。
7、然后我们来考虑背面剔除(Back-Face Removal (Culling)):面是可见的,当且仅当视线向量与法向量的夹角θ在90°~-90°之间,等价于cosθ≥0或者v • n≥0。平面具有参数形式ax + by +cz +d =0,但对于规范化视线向量V = ( 0 0 1 0)T ,由于视线方向V为正,只需要检测符号c 正负值(c代表平面的法向在z轴上的投影)即可。
为了丢弃一些被OPENGL认为需要剔除(凸的才正确)的多边形,可调用剔除相关函数:
首先调用:glEnable(GL_CULL_FACE)启用剔除功能。
然后调用:glCullFace(GLenum mode),其中mode 参数为剔除哪些面,比如GL_FRONT、GL_BACK、GL_FRONT_AND_BACK,缺省为GL_BACK。
默认的正面是glFrontFace(GL_CCW),默认的剔除是glCullFace(GL_BACK)。避免光照、阴影和颜色计算及操作,消除相关渲染计算开销。
8、Z-Buffer Algorithm深度缓存算法(后续详解):


9、Scan-Line Algorithm扫描线算法(后续详解):


10、许多实时应用系统中(例如游戏),我们希望能在应用程序中消除尽可能多的不可见对象,从而降低流水线体系的负担、减少出现数据通信阻塞的可能。考虑BSP二叉空间剖分法:
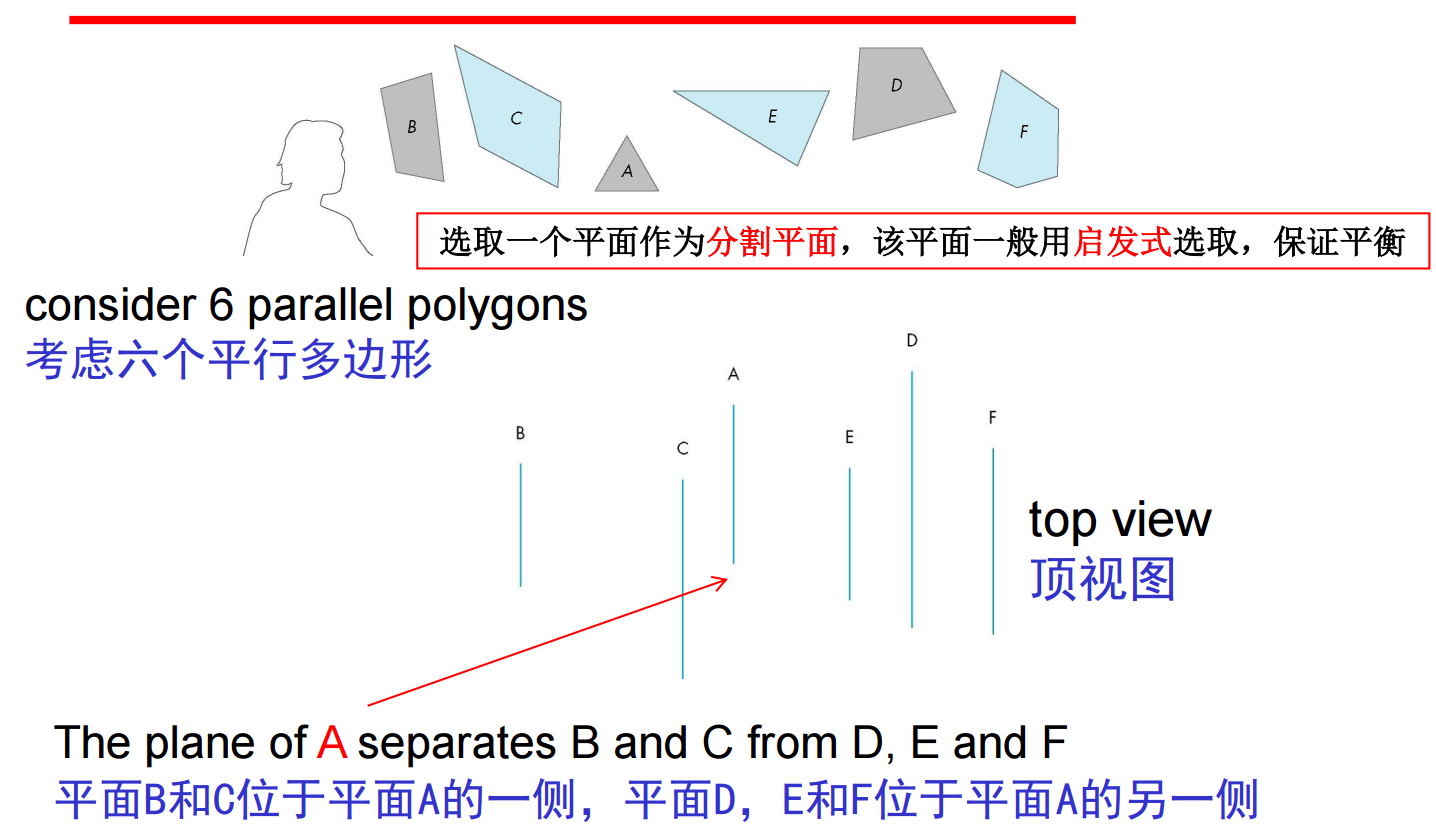
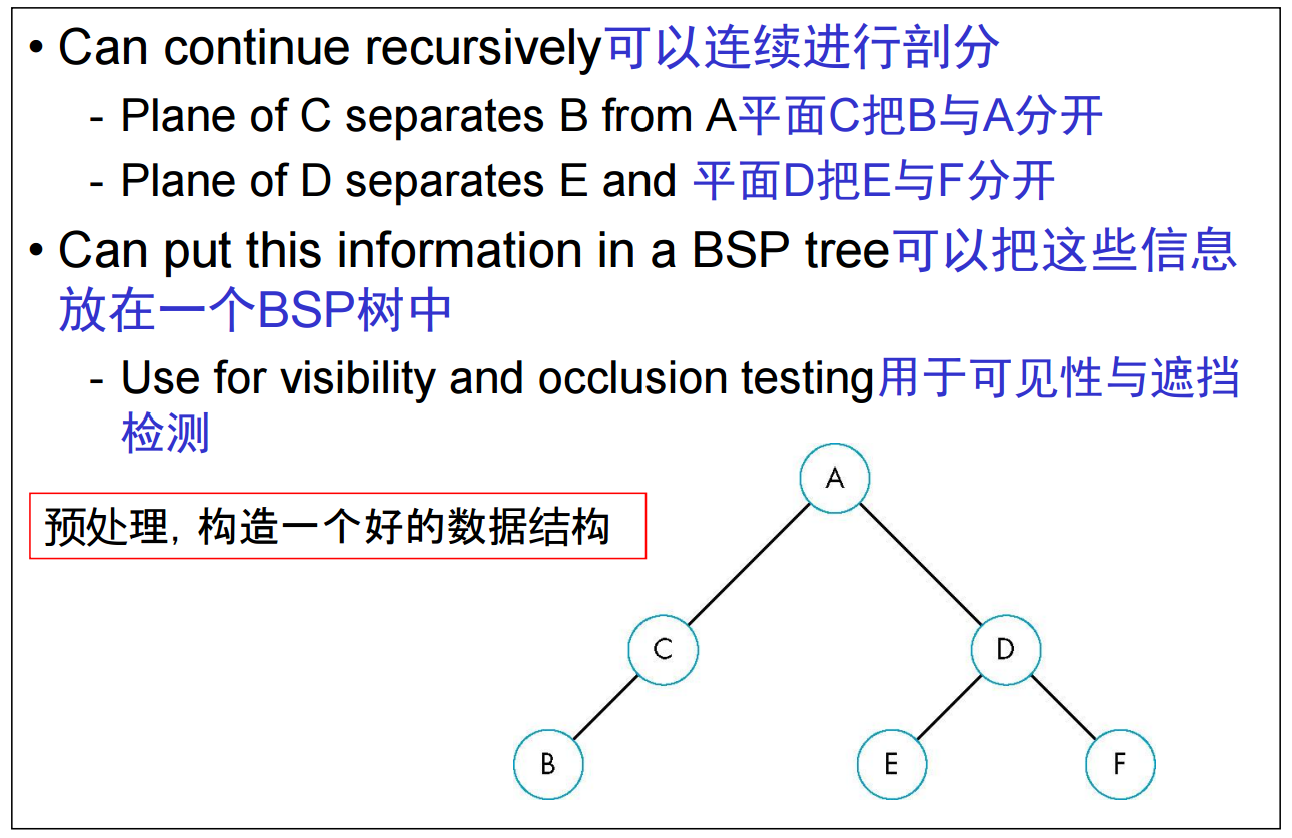
BSP树有很多应用。例如,消隐藏算法中,结合BSP树的背面剔除算法。根据背面剔除算法可知,当前分割面相对视点是否可见;而根据BSP树可知,视点处在分割面的前面还是后面。①如果分割面不可见,并且视点在分割面的后面,则判断出视线方向是离开分割面,只有在分割面后面的面才有可能可见;在该分割面前面的所有的面都是绝对不可见的,剔除(后一页)。②如果分割面不可见,并且视点在分割面的前面,则判断出视线方向是离开分割面,只有在分割面前面的面才有可能可见;在该分割面后面的所有的面都是绝对不可见的,剔除(后二页)。这样就可以高效地剔除大量三角形面片。
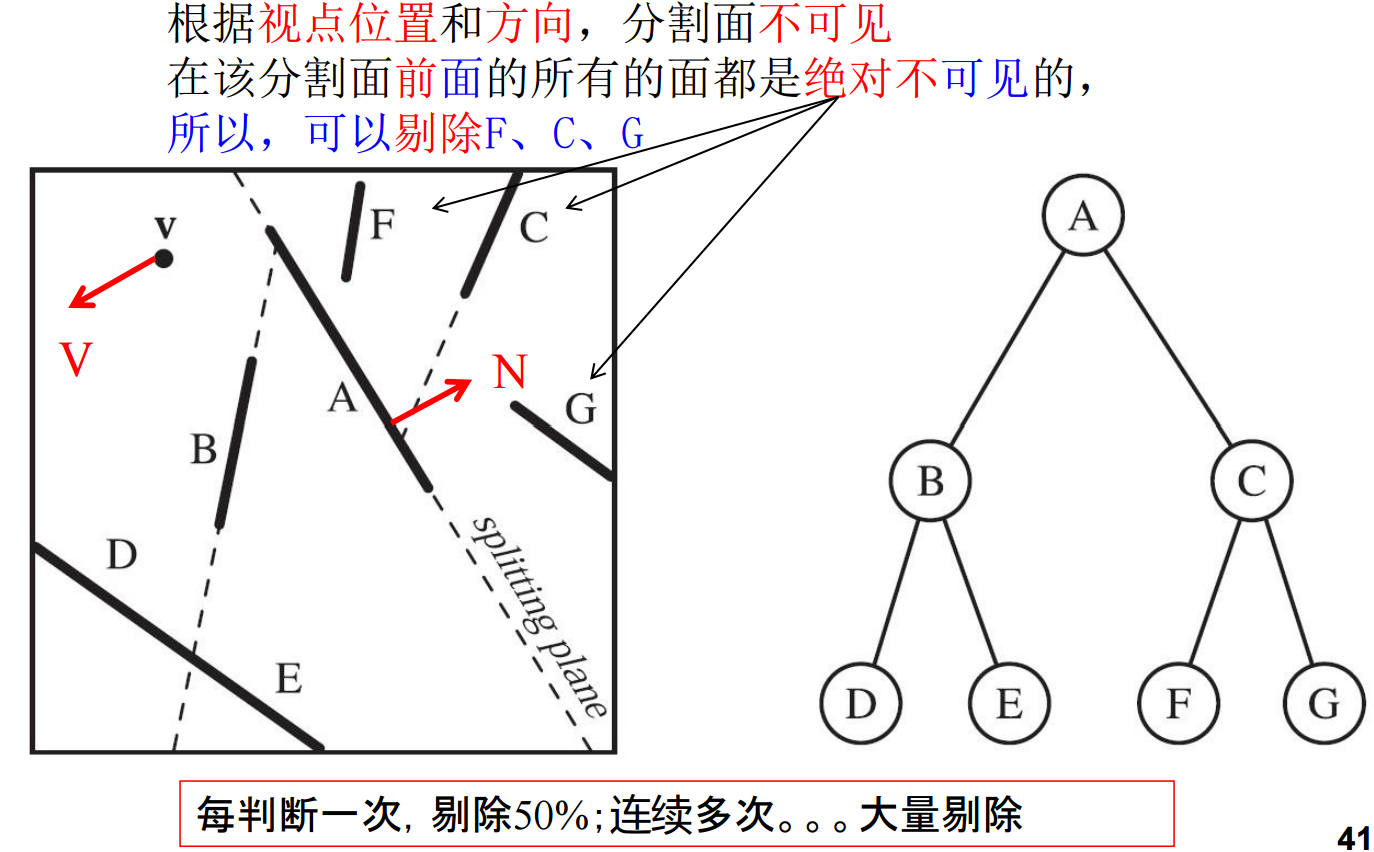
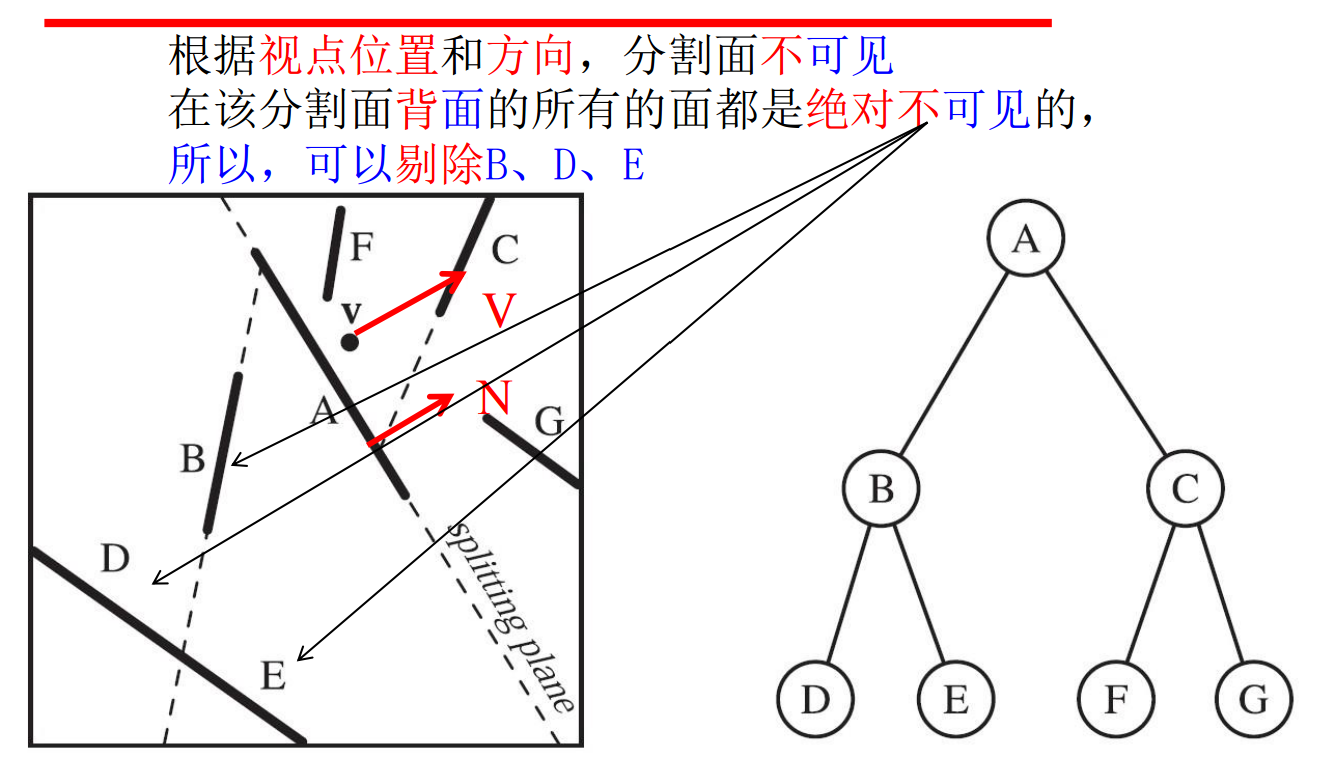
这种结合BSP树的背面剔除特点是预先构建BSP数据结构(离线构造),然后实时在线调用,效率高。明显的缺点是需要额外存储空间、只适合静态场景(否则重新划分)。其一般意义是,这是典型的一类空间换时间的算法模式;好的数据结构有助于提高算法效率,二者紧密相关。