在深度学习和机器学习中,损失函数是模型训练的指南针,它告诉模型当前预测与真实目标之间的差距有多大,指导模型如何调整参数以减少这个差距。
在众多损失函数中,交叉熵损失函数 无疑是分类任务中最重要、最常用的损失函数。从图像分类到自然语言处理,从简单的二分类到复杂的多标签分类,交叉熵损失都扮演着关键角色。
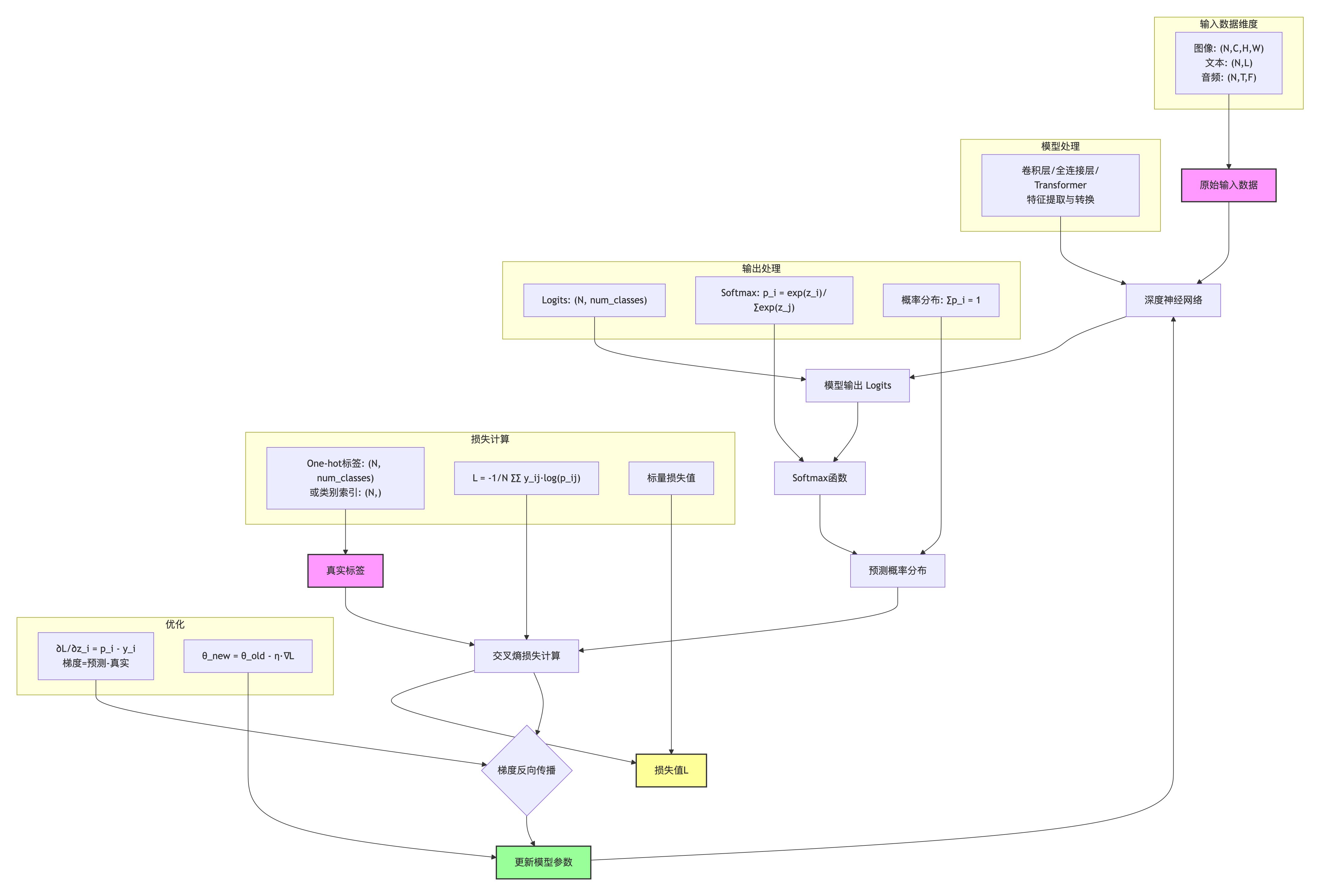
一、什么是交叉熵损失?
交叉熵(Cross-Entropy)源于信息论,是衡量两个概率分布之间差异的指标。在机器学习中,我们用它来衡量模型预测的概率分布 与真实的标签分布之间的差异。
信息论基础
要理解交叉熵,首先需要了解几个基本概念:
- 信息量 :一个事件发生的概率越低,其信息量越大。定义为 I(x)=−logP(x)I(x) = -\log P(x)I(x)=−logP(x)
- 熵 :衡量一个概率分布的不确定性。定义为 H(p)=−∑p(x)logp(x)H(p) = -\sum p(x)\log p(x)H(p)=−∑p(x)logp(x)
- KL散度:衡量两个概率分布之间的差异
- 交叉熵:用分布q表示分布p所需的平均编码长度
从KL散度到交叉熵
KL散度(Kullback-Leibler Divergence)衡量两个概率分布p和q的差异:
DKL(p∥q)=∑xp(x)logp(x)q(x) D_{KL}(p \| q) = \sum_x p(x) \log \frac{p(x)}{q(x)} DKL(p∥q)=x∑p(x)logq(x)p(x)
展开后得到:
DKL(p∥q)=−∑xp(x)logq(x)⏟交叉熵−(−∑xp(x)logp(x))⏟p的熵 D_{KL}(p \| q) = \underbrace{-\sum_x p(x) \log q(x)}{\text{交叉熵}} - \underbrace{\left(-\sum_x p(x) \log p(x)\right)}{\text{p的熵}} DKL(p∥q)=交叉熵 −x∑p(x)logq(x)−p的熵 (−x∑p(x)logp(x))
由于p的熵是固定的,最小化KL散度等价于最小化交叉熵。这就是为什么在分类任务中,我们最小化交叉熵损失。
二、数学公式详解
二分类交叉熵
对于二分类问题,交叉熵损失公式为:
L=−1N∑i=1N[yilog(pi)+(1−yi)log(1−pi)] L = -\frac{1}{N} \sum_{i=1}^N [y_i \log(p_i) + (1-y_i) \log(1-p_i)] L=−N1i=1∑N[yilog(pi)+(1−yi)log(1−pi)]
其中:
- NNN:样本数量
- yiy_iyi:第i个样本的真实标签(0或1)
- pip_ipi:模型预测第i个样本为正类的概率
这个公式可以理解为:对于正样本(yi=1y_i=1yi=1),我们希望pip_ipi尽可能接近1;对于负样本(yi=0y_i=0yi=0),我们希望pip_ipi尽可能接近0。
多分类交叉熵
对于多分类问题,交叉熵损失公式为:
L=−1N∑i=1N∑c=1Cyi,clog(pi,c) L = -\frac{1}{N} \sum_{i=1}^N \sum_{c=1}^C y_{i,c} \log(p_{i,c}) L=−N1i=1∑Nc=1∑Cyi,clog(pi,c)
其中:
- CCC:类别数量
- yi,cy_{i,c}yi,c:第i个样本属于类别c的真实概率(通常是one-hot编码)
- pi,cp_{i,c}pi,c:模型预测第i个样本属于类别c的概率
在实际应用中,yi,cy_{i,c}yi,c通常是one-hot向量,即只有真实类别位置为1,其余为0。因此公式可以简化为:
L=−1N∑i=1Nlog(pi,yi) L = -\frac{1}{N} \sum_{i=1}^N \log(p_{i,y_i}) L=−N1i=1∑Nlog(pi,yi)
其中yiy_iyi是样本i的真实类别索引。
Softmax函数
在多分类问题中,模型的原始输出(称为logits)需要通过softmax函数转换为概率分布:
pi,c=ezi,c∑j=1Cezi,j p_{i,c} = \frac{e^{z_{i,c}}}{\sum_{j=1}^C e^{z_{i,j}}} pi,c=∑j=1Cezi,jezi,c
其中zi,cz_{i,c}zi,c是模型对第i个样本在第c个类别上的原始得分(logit)。
Softmax函数确保:
- 所有类别的概率之和为1:∑c=1Cpi,c=1\sum_{c=1}^C p_{i,c} = 1∑c=1Cpi,c=1
- 每个概率都在0到1之间:0≤pi,c≤10 \leq p_{i,c} \leq 10≤pi,c≤1
三、PyTorch中的实现与数据维度
在PyTorch中,交叉熵损失通过nn.CrossEntropyLoss类实现。理解其输入输出的数据维度要求至关重要。
输入维度要求
nn.CrossEntropyLoss对输入数据有严格的维度要求:
1. 标准分类任务
-
预测值(Input) :形状为
(N, C)N:批次大小(batch size)C:类别数量- 注意:输入应该是原始logits,不要预先做softmax
-
目标值(Target) :形状为
(N,)- 每个元素是类别索引,取值范围为[0, C-1]
- 数据类型应为
torch.long
示例:
python
import torch
import torch.nn as nn
predictions = torch.randn(4, 3) # 形状: (4, 3)
labels = torch.tensor([0, 2, 1, 0]) # 形状: (4,)
loss_fn = nn.CrossEntropyLoss()
loss = loss_fn(predictions, labels)
print(loss)
clike
tensor(1.4208)2. 序列标注任务
- 预测值 :形状为
(N, C, L)L:序列长度
- 目标值 :形状为
(N, L)- 每个位置是类别索引
示例(命名实体识别):
python
import torch
import torch.nn as nn
# 批次大小=2,类别数=5,序列长度=10
predictions = torch.randn(2, 5, 10) # (N, C, L)
labels = torch.randint(0, 5, (2, 10)) # (N, L)
loss_fn = nn.CrossEntropyLoss()
loss = loss_fn(predictions, labels)
print(loss)
clike
tensor(1.5822)3. 图像分割任务
- 预测值 :形状为
(N, C, H, W)H:图像高度W:图像宽度
- 目标值 :形状为
(N, H, W)- 每个像素是类别索引
示例(语义分割):
python
import torch
import torch.nn as nn
loss_fn = nn.CrossEntropyLoss()
# 批次大小=2,类别数=21,图像尺寸224×224
predictions = torch.randn(2, 21, 224, 224) # (N, C, H, W)
labels = torch.randint(0, 21, (2, 224, 224)) # (N, H, W)
loss = loss_fn(predictions, labels)
print(loss)
clike
tensor(3.5042)维度匹配规则总结
| 任务类型 | 预测值形状 | 目标值形状 | 说明 |
|---|---|---|---|
| 标准分类 | (N, C) | (N,) | 最常见情况 |
| 序列标注 | (N, C, L) | (N, L) | L为序列长度 |
| 图像分割 | (N, C, H, W) | (N, H, W) | 像素级分类 |
| 3D分割 | (N, C, D, H, W) | (N, D, H, W) | 体积数据分类 |
关键规则 :目标值总是比预测值少一个维度,少的是类别维度(C)。
四、梯度推导与反向传播
理解交叉熵损失的梯度对于深入理解模型训练过程非常重要。
梯度公式推导
对于单个样本,设:
- 真实标签的one-hot向量为 yyy(CCC维)
- 模型预测的概率分布为 ppp(CCC维)
- 原始logits为 zzz(CCC维)
交叉熵损失为:
L=−∑c=1Cyclog(pc) L = -\sum_{c=1}^C y_c \log(p_c) L=−c=1∑Cyclog(pc)
其中 pc=softmax(zc)=ezc∑j=1Cezjp_c = \text{softmax}(z_c) = \frac{e^{z_c}}{\sum_{j=1}^C e^{z_j}}pc=softmax(zc)=∑j=1Cezjezc
计算损失对logits的梯度:
∂L∂zi=pi−yi \frac{\partial L}{\partial z_i} = p_i - y_i ∂zi∂L=pi−yi
直观理解:梯度是预测概率与真实概率的差值。当预测正确时,梯度较小;预测错误时,梯度较大,推动模型修正预测。
梯度特性
- 方向明确:梯度指向正确的方向,推动预测向真实标签移动
- 数值稳定:梯度值在[-1, 1]范围内,避免梯度爆炸
- 效率高:梯度计算简单,只需一次减法操作