详解Splay平衡树

目录

• • *引言*
  • 算法能解决的问题
  • 算法原理
  • • 树的旋转操作
    • 算法时间复杂度
    • Splay操作
    • [将一段序列插入到 y y y后面](#将一段序列插入到 y y y后面)
    • 删除序列的一段
  • 模板代码实现
  • 例题
  • • 郁闷的出纳员
    • [HNOI2012 永无乡](#HNOI2012 永无乡)

引言

如果没了解过线段树, 点击这里

算法能解决的问题

首先Splay是平衡二叉树 , 也就是该树的中序遍历是有序的, 可以实现查询第 k k k大数, 查询一个数字的前驱 和后继

Splay的特殊操作, 可以支持区间翻转 , 可以处理很多线段树能处理的问题(因为可以加入延迟标记)

算法原理

树的旋转操作

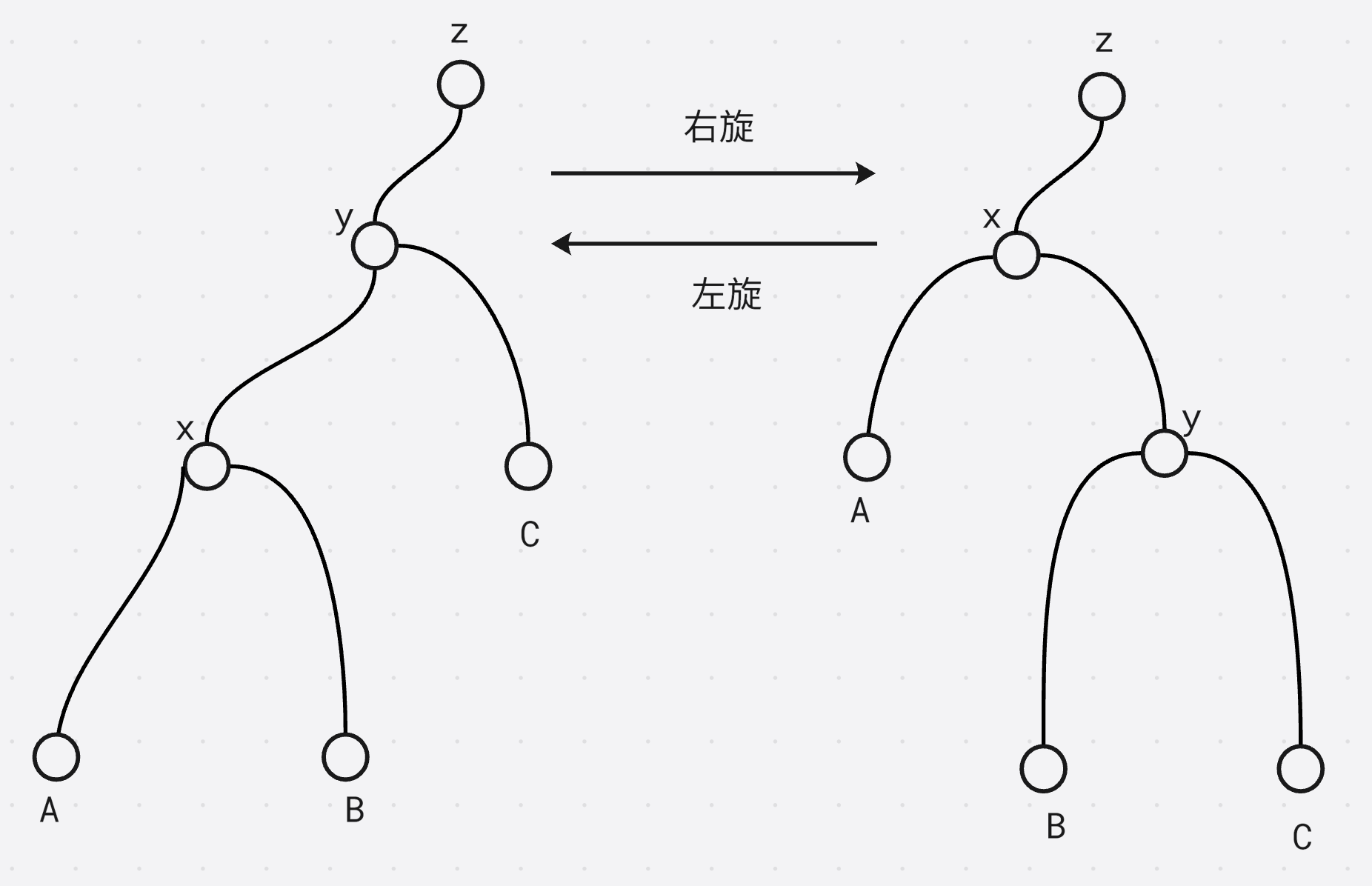
注意在旋转前后需要保证中序遍历不会发生变化

对于节点 B B B, 在旋转之前 x ≤ B ≤ y x \le B \le y x≤B≤y, 旋转之后也是这样的大小关系

算法时间复杂度

算法核心 :不管对Splay进行什么操作, 将当前操作的点旋转到树根 r o o t root root

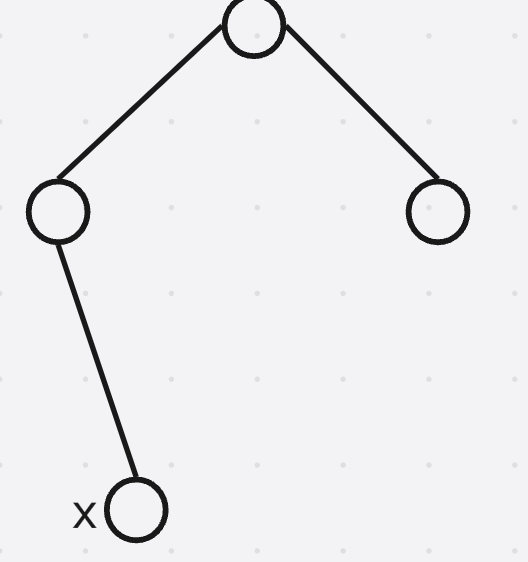
假设插入的是 x x x节点, 将节点转到树根

这样操作已经证明了, 均摊时间复杂度 O ( log ⁡ n ) O(\log n) O(logn)

Splay操作

实现 s p l a y ( x , k ) splay(x, k) splay(x,k), 将点 x x x旋转到 k k k下面

• 情况一

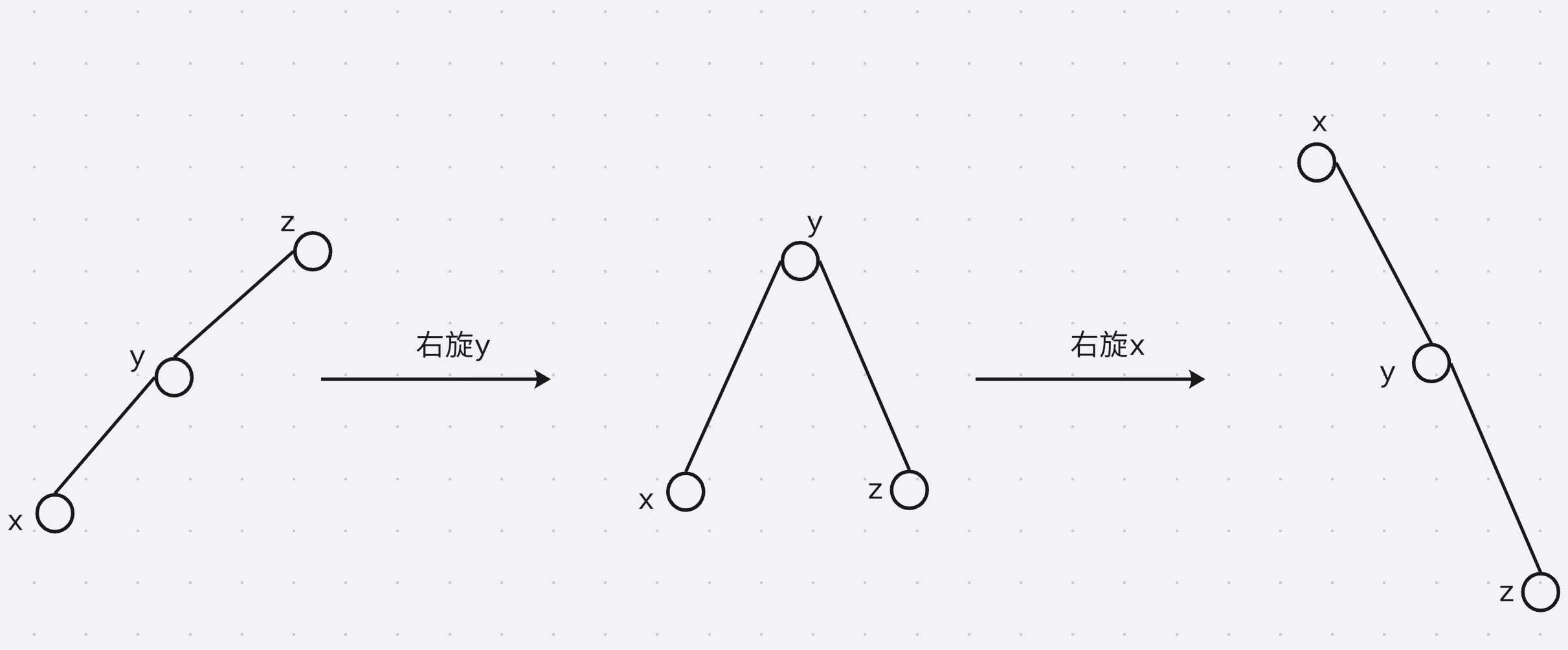
• 情况二

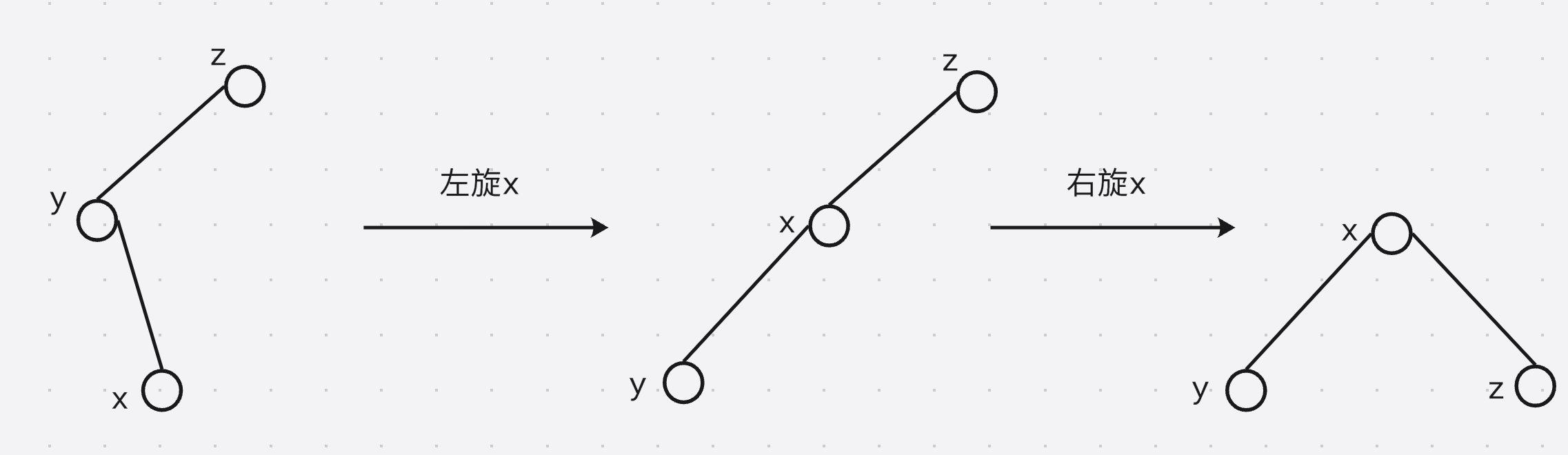
剩余情况和上面情况对称, 可以理解为

• 如果是直线, 先转 y y y, 再转 x x x, 如果是折线
• 如果是折线, 转两次 x x x

将一段序列插入到 y y y后面

假设 y y y的后继是 t t t

1. 将 y y y转到根节点
2. 将 t t t转到 y y y的下方

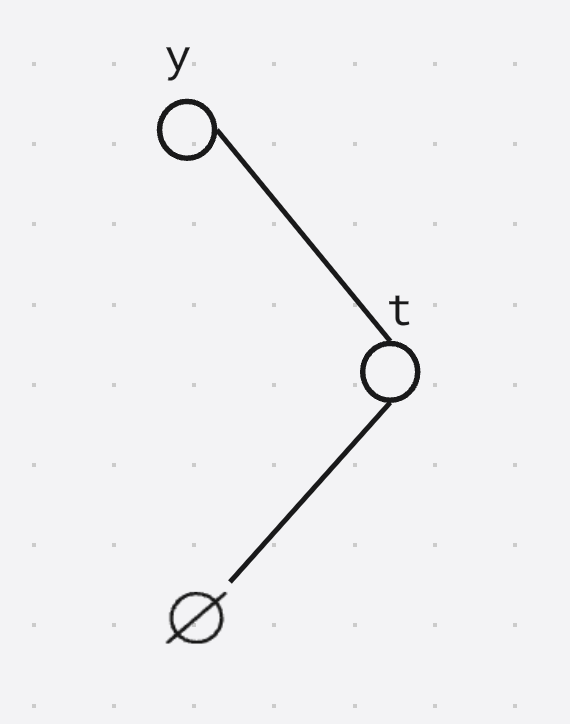
因为 t t t是 y y y的后继, t t t的左子树是空集

3. 直接将序列插入到 t t t的左子树

删除序列的一段

假设删除序列 [ l , r ] [l, r] [l,r], l l l的前驱是 u u u, r r r的后继是 v v v

1. 先将 u u u转到根节点
2. 将 v v v转到 u u u的下方
3. 删除 v v v的左子树

模板代码实现

1. 找第 k k k个数, 需要维护每个子树的节点个数
2. 翻转区间, 维护一个延迟标记 r e v rev rev

类似于线段树, 树形结构需要通过儿子信息计算根节点信息 , push up操作

翻转的延迟标记需要下传 需要push down操作

旋转的核心函数

void rotate(int x) {
    int y = tr[x].p, z = tr[y].p;
    // k = 0代表x是y的左儿子, 右旋, 反之则左旋
    int k = tr[y].s[1] == x;
    tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    // 因为旋转后y在x下面, 需要先pushup(y)
    pushup(y), pushup(x);
}

splay核心操作

// 将x旋转到k的下方, 特别的, 如果k == 0, 将x转到根节点位置
void splay(int x, int k) {
    while (tr[x].p != k) {
        int y = tr[x].p, z = tr[y].p;
        // 如果z == k, 只需要转1次x就能到达目标位置
        if (z != k) {
            if ((tr[z].s[1] == y) ^ (tr[y].s[1] == x)) rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
    if (!k) root = x;
}

代码实现

为什么操作之后不能 将节点转到 r o o t root root?

• 相当于我将一个打上标记的点转到了根, 这样整个树的节点的翻转标记都会改变! , 这是严重错误的
• 实际我需要的是将该位置打上标记不移动, 只有询问到改位置的时候再将延迟标记下传, 使延迟标记生效
• 只有该节点上的延迟标记生效后(下传或者清空后 ), 才可以将该节点 旋转到 r o o t root root

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int n, m;
struct Node {
    int s[2], p;
    int cnt, rev, v;
    void init(int _v, int _p) {
        p = _p;
        v = _v;
        cnt = 1, rev = 0;
    }
} tr[N];
int root, idx;

void pushup(int u) {
    tr[u].cnt = tr[tr[u].s[0]].cnt + tr[tr[u].s[1]].cnt + 1;
}

void pushdown(int u) {
    if (tr[u].rev) {
        swap(tr[u].s[0], tr[u].s[1]);
        tr[tr[u].s[0]].rev ^= 1;
        tr[tr[u].s[1]].rev ^= 1;
        tr[u].rev = 0;
    }
}

void rotate(int x) {
    int y = tr[x].p, z = tr[y].p;
    // k = 0代表x是y的左儿子, 右旋, 反之则左旋
    int k = tr[y].s[1] == x;
    tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    // 因为旋转后y在x下面, 需要先pushup(y)
    pushup(y), pushup(x);
}

// 将x旋转到k的下方, 特别的, 如果k == 0, 将x转到根节点位置
void splay(int x, int k) {
    while (tr[x].p != k) {
        int y = tr[x].p, z = tr[y].p;
        // 如果z == k, 只需要转1次x就能到达目标位置
        if (z != k) {
            if ((tr[z].s[1] == y) ^ (tr[y].s[1] == x)) rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
    if (!k) root = x;
}

void insert(int val) {
    int u = root, p = 0;
    while (u) {
        p = u;
        u = tr[u].s[val > tr[u].v];
    }
    u = ++idx;
    if (p) tr[p].s[val > tr[p].v] = u;
    tr[u].init(val, p);
    splay(u, 0);
}

int get_k(int u, int k) {
    pushdown(u);
    int cnt = tr[tr[u].s[0]].cnt + 1;
    if (k < cnt) return get_k(tr[u].s[0], k);
    if (k == cnt) return u;
    return get_k(tr[u].s[1], k - cnt);
}

void dfs(int u) {
    pushdown(u);
    if (tr[u].s[0]) dfs(tr[u].s[0]);
    if (tr[u].v >= 1 && tr[u].v <= n) cout << tr[u].v << ' ';
    if (tr[u].s[1]) dfs(tr[u].s[1]);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> m;

    // 初始化序列, 添加两个哨兵
    for (int i = 0; i <= n + 1; ++i) insert(i);

    while (m--) {
        int l, r;
        cin >> l >> r;

        int x = get_k(root, l), y = get_k(root, r + 2);
        splay(x, 0), splay(y, x);

        tr[tr[y].s[0]].rev ^= 1;
        // splay(tr[y].s[0], 0); 这里不能splay
    }

    dfs(root);

    return 0;
}

例题

郁闷的出纳员

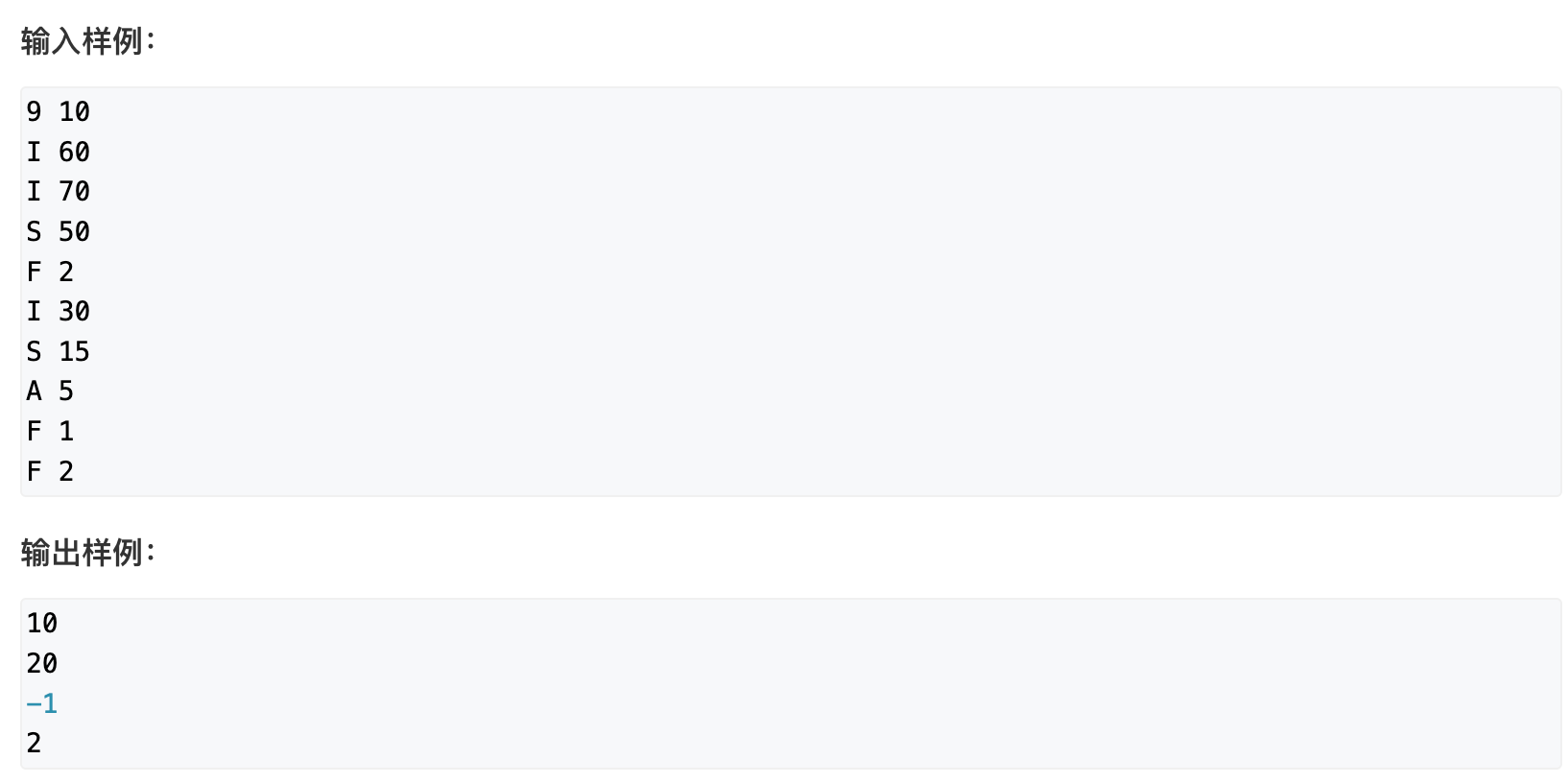
因为每次操作都是对所有员工 , 可以记录一个偏移量 o f f s e t offset offset, 员工的真实工资 是 x + o f f s e t x + offset x+offset, 每次删除是 x < m i n − o f f s e t x < min - offset x<min−offset的员工, 区间删除可以使用splay实现

代码实现

注意:
get函数返回的是节点索引 , 需要取值, 并且计算最终薪资的时候需要加偏移量 o f f s e t offset offset, 并且根节点不是 0 0 0 , 而是 r o o t root root!

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10, INF = 1e9;

int n, minv, offs;
struct Node {
    int s[2], p;
    int v, cnt;
    void init(int _v, int _p) {
        v = _v, p  =_p;
        cnt = 1;
        s[0] = s[1] = 0;
    }
} tr[N];
int root, idx;

void pushup(int u) {
    tr[u].cnt = tr[tr[u].s[0]].cnt + tr[tr[u].s[1]].cnt + 1;
}

void rotate(int x) {
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}

void splay(int x, int k) {
    while (tr[x].p != k) {
        int y = tr[x].p, z = tr[y].p;
        if (z != k) {
            if ((tr[z].s[1] == y) ^ (tr[y].s[1] == x)) rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
    if (!k) root = x;
}

int insert(int val) {
    int u = root, p = 0;
    while (u) {
        p = u;
        u = tr[u].s[val > tr[u].v];
    }

    u = ++idx;
    if (p) tr[p].s[val > tr[p].v] = u;
    tr[u].init(val, p);
    splay(u, 0);
    return u;
}

// 返回第K小数的节点索引
int get_k(int u, int k) {
    int cnt = tr[tr[u].s[0]].cnt + 1;
    if (k < cnt) return get_k(tr[u].s[0], k);
    if (k == cnt) return u;
    return get_k(tr[u].s[1], k - cnt);
}

// 计算 >= val的最小的节点索引
int get(int val) {
    int u = root, ans = 0;

    while (u) {
        if (tr[u].v >= val) {
            ans = u;
            u = tr[u].s[0];
        }
        else u = tr[u].s[1];
    }

    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> minv;

    // 添加两个哨兵
    int L = insert(-INF);
    insert(INF);

    int tot = 0;
    while (n--) {
        char c;
        int k;
        cin >> c >> k;
        if (c == 'I') {
            if (k < minv) continue;
            k -= offs;
            tot++;
            insert(k);
        }
        else if (c == 'A') offs += k;
        else if (c == 'S') {
            offs -= k;
            int x = L;
            int y = get(minv - offs);
            splay(x, 0), splay(y, x);
            tr[y].s[0] = 0;
            pushup(y), pushup(x);
        }
        else {
            if (k > tr[root].cnt - 2) cout << -1 << '\n';
            else {
                int idx = get_k(root, tr[root].cnt - k);
                cout << tr[idx].v + offs << '\n';
            }
        }
    }

    cout << tot - (tr[root].cnt - 2) << '\n';

    return 0;
}

HNOI2012 永无乡

n ≤ 1 0 5 n \le 10 ^ 5 n≤105, m ≤ 1 0 5 m \le 10 ^ 5 m≤105, q ≤ 3 × 1 0 5 q \le 3 \times 10 ^ 5 q≤3×105

可以使用并查集维护节点 x x x的代表元素, 假设是 p x p_x px

暴力做法是并查集 + 排序, 算法时间复杂度 O ( q × n log ⁡ n ) O(q \times n \log n) O(q×nlogn), 一定无法通过

• 因为涉及到排名查询 , 和岛屿合并 , 并且查询集合的第 k k k小数 , 可以考虑使用线段树 或者 s p l a y splay splay实现
• root[p[x]]代表 x x x所在集合代表元素的线段树或者 s p l a y splay splay中的节点下标
• s p l a y splay splay维护的中序遍历是重要程度的排名 , 因为题目要求查询第 k k k小重要程度的岛屿编号

线段树实现

因为线段树涉及合并操作 , 需要动态开点 的线段树 , 在合并的时候可以启发式合并优化

• 因为需查询排名, 线段树需要记录节点数量信息
• 当二分到当前节点 需要记录岛屿节点编号 i d id id

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int n, m, q;
int p[N];
struct Node {
    int ls, rs;
    int cnt, id;
} tr[4 * N + 17 * N];
int root[N], idx;

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void pushup(int u) {
    tr[u].cnt = tr[tr[u].ls].cnt + tr[tr[u].rs].cnt;
}

int build(int l, int r, int x, int id) {
    int u = ++idx;
    if (l == r) {
        tr[u].cnt++;
        tr[u].id = id;
        return u;
    }

    int mid = l + r >> 1;
    if (x <= mid) tr[u].ls = build(l, mid, x, id);
    if (x > mid) tr[u].rs = build(mid + 1, r, x, id);

    pushup(u);
    return u;
}

// 将v合并到u
int merge(int u, int v, int l, int r) {
    if (!u) return v;
    if (!v) return u;

    if (l == r) {
        tr[u].cnt += tr[v].cnt;
        return u;
    }

    int mid = l + r >> 1;
    tr[u].ls = merge(tr[u].ls, tr[v].ls, l, mid);
    tr[u].rs = merge(tr[u].rs, tr[v].rs, mid + 1, r);
    pushup(u);

    return u;
}

int query(int u, int l, int r, int k) {
    if (l == r) return tr[u].id;

    int cnt = tr[tr[u].ls].cnt;
    int mid = l + r >> 1;
    if (cnt >= k) return query(tr[u].ls, l, mid, k);
    return query(tr[u].rs, mid + 1, r, k - cnt);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        int x;
        cin >> x;
        // 为每个岛屿构建线段树, 并且初始化并查集
        root[i] = build(1, n, x, p[i] = i);
    }

    while (m--) {
        int a, b;
        cin >> a >> b;
        int fa = find(a), fb = find(b);
        if (fa == fb) continue;

        // 将两座岛屿的并查集和线段树合并
        int cnt1 = tr[root[fa]].cnt;
        int cnt2 = tr[root[fb]].cnt;
        if (cnt1 < cnt2) {
            p[fa] = fb;
            root[fb] = merge(root[fb], root[fa], 1, n);
        }
        else {
            p[fb] = fa;
            root[fa] = merge(root[fa], root[fb], 1, n);
        }
    }

    cin >> q;
    while (q--) {
        char op;
        cin >> op;
        if (op == 'B') {
            int a, b;
            cin >> a >> b;

            int fa = find(a), fb = find(b);
            if (fa == fb) continue;

            // 将两座岛屿的并查集和线段树合并
            int cnt1 = tr[root[fa]].cnt;
            int cnt2 = tr[root[fb]].cnt;
            if (cnt1 < cnt2) {
                p[fa] = fb;
                root[fb] = merge(root[fb], root[fa], 1, n);
            }
            else {
                p[fb] = fa;
                root[fa] = merge(root[fa], root[fb], 1, n);
            }
        }
        // 查询x所在连通块的排名第K小的岛屿编号
        else {
            int x, k;
            cin >> x >> k;
            int p = find(x);
            if (tr[root[p]].cnt < k) cout << -1 << '\n';
            else cout << query(root[p], 1, n, k) << '\n';
        }
    }

    return 0;
}

splay实现

#include <bits/stdc++.h>

using namespace std;

const int N = 5e5 + 10;

int n, m, q;
struct Node {
    int s[2], p;
    int v, id, cnt;
    void init(int _v, int _id, int _p) {
        v = _v;
        id = _id;
        p = _p;
        cnt = 1;
    }
} tr[N];
int root[N], idx;
int p[N];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void pushup(int u) {
    tr[u].cnt = tr[tr[u].s[0]].cnt + tr[tr[u].s[1]].cnt + 1;
}

void rotate(int x) {
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}

void splay(int s, int x, int k) {
    while (tr[x].p != k) {
        int y = tr[x].p, z = tr[y].p;
        if (z != k) {
            if ((tr[z].s[1] == y) ^ (tr[y].s[1] == x)) rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
    if (!k) root[s] = x;
}

void insert(int s, int v, int id) {
    int u = root[s], p = 0;
    while (u) {
        p = u;
        u = tr[u].s[v > tr[u].v];
    }
    u = ++idx;
    tr[u].init(v, id, p);
    if (p) tr[p].s[v > tr[p].v] = u;
    splay(s, u, 0);
}

int get_k(int u, int k) {
    if (!u) return -1;
    int cnt = tr[tr[u].s[0]].cnt + 1;
    if (cnt > k) return get_k(tr[u].s[0], k);
    if (cnt == k) return tr[u].id;
    return get_k(tr[u].s[1], k - cnt);
}

void merge(int s, int v) {
    if (!v) return;
    if (tr[v].s[0]) merge(s, tr[v].s[0]);
    if (tr[v].s[1]) merge(s, tr[v].s[1]);
    insert(s, tr[v].v, tr[v].id);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        int v;
        cin >> v;
        root[i] = p[i] = i;
        tr[i].init(v, i, 0);
    }
    idx = n;

    while (m--) {
        int a, b;
        cin >> a >> b;
        int fa = find(a), fb = find(b);
        if (fa == fb) continue;
        int cnt1 = tr[root[fa]].cnt, cnt2 = tr[root[fb]].cnt;
        if (cnt1 < cnt2) swap(fa, fb);
        p[fb] = fa;
        merge(fa, root[fb]);
    }

    cin >> q;
    while (q--) {
        char op;
        cin >> op;
        if (op == 'B') {
            int a, b;
            cin >> a >> b;
            int fa = find(a), fb = find(b);
            if (fa == fb) continue;
            int cnt1 = tr[root[fa]].cnt, cnt2 = tr[root[fb]].cnt;
            if (cnt1 < cnt2) swap(fa, fb);
            p[fb] = fa;
            merge(fa, root[fb]);
        }
        else {
            int x, k;
            cin >> x >> k;
            int p = find(x);
            if (tr[root[p]].cnt < k) cout << -1 << '\n';
            else cout << get_k(root[p], k) << '\n';
        }
    }

    return 0;
}