脑网络连接性:时域与频域方法的分析
摘要:在脑电图(EEG)数据分析中,如何选择正确的连接性(Connectivity)指标一直是个焦点问题。是选格兰杰因果(GC)?还是部分定向相干(PDC)?时域和频域到底有什么区别?
本文基于 2023 年发表在 Bioengineering 上的高分综述论文 《Connectivity Analysis in EEG Data: A Tutorial Review of the State of the Art and Emerging Trends》,深度解析时域与频域分析的核心差异与联系。
1. 引言:我们为什么需要连接性分析?
EEG 信号不仅包含各个电极的独立活动,更隐藏着大脑不同区域之间的动态交互。为了量化这种交互,我们需要从结构 (解剖连接)、功能 (统计依赖)和有效(因果驱动)三个维度入手。
然而,面对几十种的算法(PCC, GC, DTF, PDC, TE...),我们该如何选择?这篇综述提供了一个非常清晰的分类体系,特别是对于时域(Time-Domain) 和 频域(Frequency-Domain) 的区分至关重要。
2. 全局视野
在深入细节之前,我们需要来理清这些指标之间的关系。
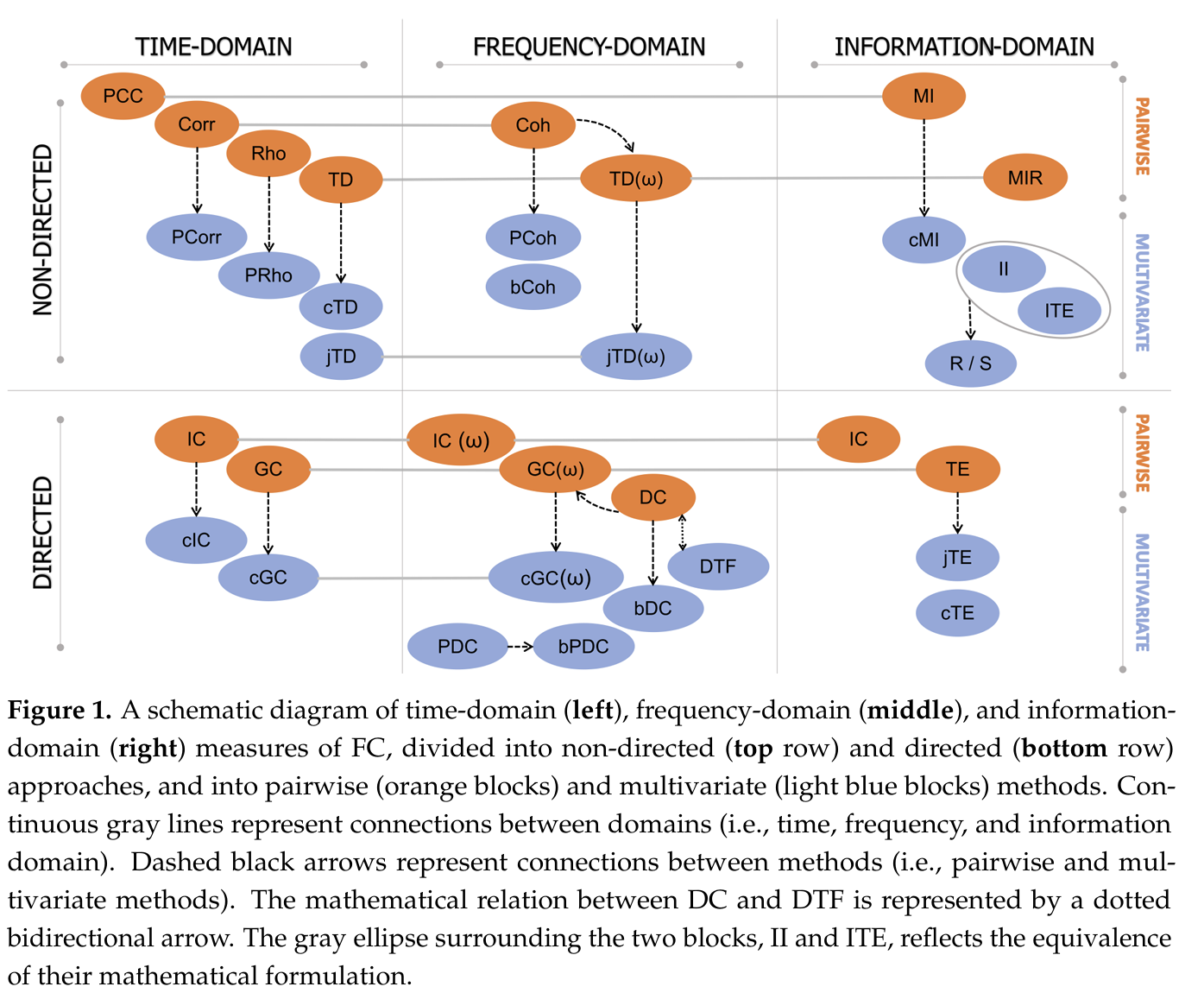
图1解说:这是整篇综述的核心分类图。
- 横轴:左侧为时域,中间为频域,右侧为信息论域。
- 纵轴:上半部分为无向连接(Coupling),下半部分为有向连接(Causality)。
- 颜色:橙色代表成对分析(Pairwise),蓝色代表多变量分析(Multivariate)。
阅读重点:
- 从橙色到蓝色 :做 EEG 网络分析时,尽量选择蓝色的多变量方法(如 PDC, DTF, cGC)。因为大脑是一个复杂网络,成对分析(橙色)容易将 A->B->C 的间接连接误判为 A->C 的直接连接。
- 域的对应:注意图中的灰色横向实线。这些线代表了Geweke 分解(积分等价性)。
3. 时域分析 (Time-Domain)
时域方法的核心关注点是时间序列的先后顺序 。其数学基础通常依赖于多元自回归模型(MVAR)。
3.1 核心逻辑:预测误差
如果利用脑区 A 的过去信息 能显著降低对脑区 B 当前信号的预测误差,我们就在时域上认为存在 A 指向 B 的因果连接。
3.2 关键指标
- 格兰杰因果 (GC):最经典的指标。它量化了引入驱动源后,预测误差方差减少的程度(取对数)。
- 互相关与相关系数 (Cross-Correlation & PCC): PCC 是"静态"的,虽然计算简单,但无法判断方向,且极易受体积导体效应(Volume Conduction) 影响
- 瞬时因果 (IC) :在 EEG 中,IC 往往包含了大量的体积导体效应(Volume Conduction) 产生的伪迹。时域分析很难区分"真正的瞬时神经交互"和"电场瞬间传导产生的虚假零延迟"。
- 总依赖性 ( TD): 定义: 衡量两个过程之间总体依赖程度的对数指标,可以分解为从 A 到 B 的 GC、从 B 到 A 的 GC 以及瞬时因果关系( IC)。
体积导体效应(Volume Conduction)
注:大脑不是绝缘体,电场会像光一样瞬间扩散,导致头皮上的不同电极记录到同一个源的信号。
3.3 优缺点总结
- 优点 :计算直接,适合分析ERP(事件相关电位) 等瞬态过程,因为这类过程主要在时间轴上展开。
- 缺点:这是一个"全频段"的混合指标,无法告诉你是 Alpha 波在通讯还是 Gamma 波在通讯。
4. 频域分析 (Frequency-Domain)
大脑通信往往发生在特定的振荡频率上(如注意力相关的 Alpha 抑制,记忆相关的 Theta 同步)。频域分析将连接性分解到具体的频率点上,这对于 EEG 尤为重要。
4.1 核心指标对比(最易混淆点)
在频域有向连接中,有三个相似指标:DC , DTF , PDC。论文对此做了极好的区分:
| 指标 | 全称 | 物理意义 | 核心优势 |
|---|---|---|---|
| DC | 定向相干性 | 描述"流入量":脑区 iii 接收的能量中,有多少比例来自脑区 jjj。 | 适合看总能量贡献。 |
| DTF | 定向传递函数 | 描述"级联影响":信号如何在网络中多级传递。 | 适合寻找网络中的源头或汇聚点。 |
| PDC | 部分定向相干性 | 描述"流出量":脑区 jjj 发出的信息,有多少直接 传给了 iii。 | 构建网络拓扑的首选。它能剔除间接路径,只保留直接连接。 |
4.2 抗干扰
针对 EEG 最大的痛点------体积导体效应,频域方法提供了独特的解决方案:
- 虚部相干性 (Imaginary Coherence):只看相干性的虚部,直接丢弃受体积导体效应影响严重的零相位滞后部分(实部)。虽然损失了部分信号,但换来了极高的可靠性。
5. 联动:Geweke 分解定理
时域和频域是割裂的吗?并不是。论文特别强调了 Geweke 分解 这一数学桥梁(见 Figure 1 中的灰色实线)。
简单来说:时域的总格兰杰因果值 = 频域谱格兰杰因果在整个频率轴上的积分。
这意味着你可以采用 "先总后分" 的策略:先在时域看两个脑区有没有连接,如果有,再切入频域看究竟是哪个频率在起作用。
6. 应用
实际处理数据时该怎么选?预处理(滤波、重采样)会对结果产生什么影响?
论文同样进行了分析
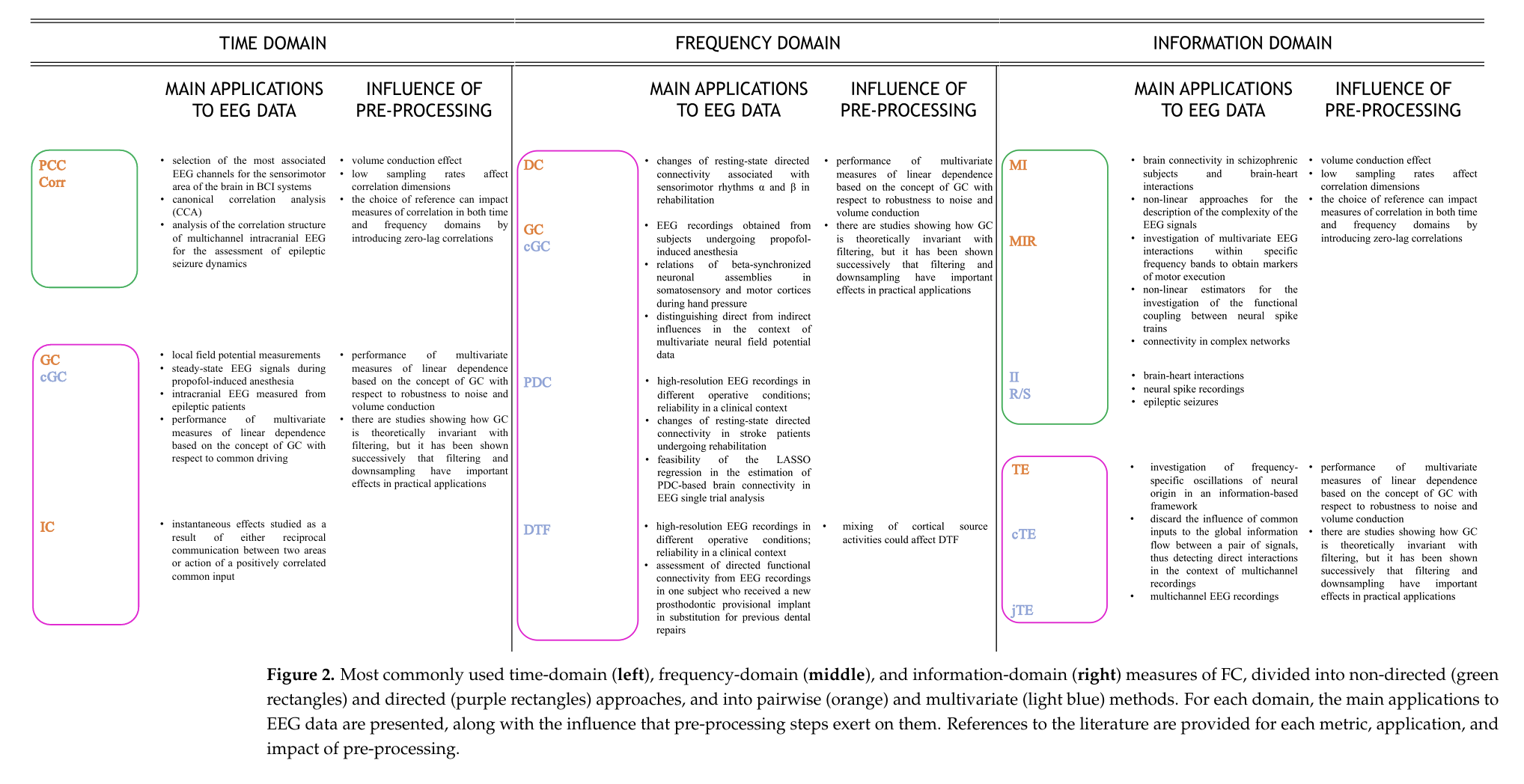
图2解说:这是论文提供的速查表。
- 左侧 (Time Domain):PCC, GC 等。
- 中间 (Frequency Domain):DC, PDC, DTF 等。
- 关注点 :每一列的 "Influence of Pre-processing"(预处理的影响)。
6.1 关键点
- 低采样率:图2中指出,过低的采样率会严重扭曲非线性指标,也会导致高频信息混叠,影响时域 GC 的计算。
- 滤波器的选择:激进的滤波器(如 IIR)会引入相位失真,这对于基于相位的频域指标(如 PLI, PDC)是致命的。建议使用零相位滤波。
- 选错指标 :如果你要做脑网络拓扑分析(画出谁连谁),选择 PDC(蓝色区域),不要用 DTF和PCC。
- 体积导体效应:如果在传感器空间(Sensor Space)做分析,必须使用抗干扰指标(如虚部相干性);或者正如论文第6节建议的,先做源定位(Source Localization),在源空间做连接性分析。
7. 总结
这篇 2023 年的综述文章为我们提供了一个清晰的 EEG 连接性分析框架:
- 时域方法(GC)适合看宏观因果和瞬态事件,但要注意伪迹。
- 频域方法(PDC, DTF)是 EEG 分析的主流,因为它能结合生理节律,且 PDC 能提供最准确的直接网络结构。
- 多变量分析优于成对分析,能有效剔除间接连接的干扰。
参考文献 :
Chiarion, G.; Sparacino, L.; Antonacci, Y.; Faes, L.; Mesin, L. Connectivity Analysis in EEG Data: A Tutorial Review of the State of the Art and Emerging Trends. Bioengineering 2023 , 10, 372.