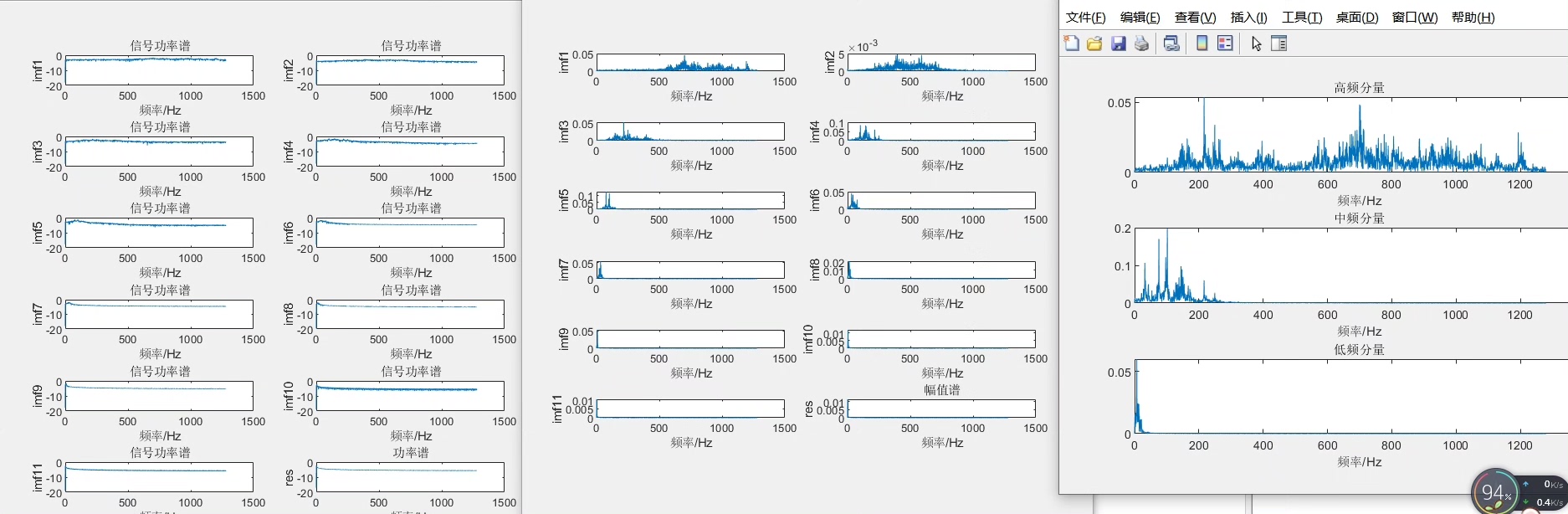
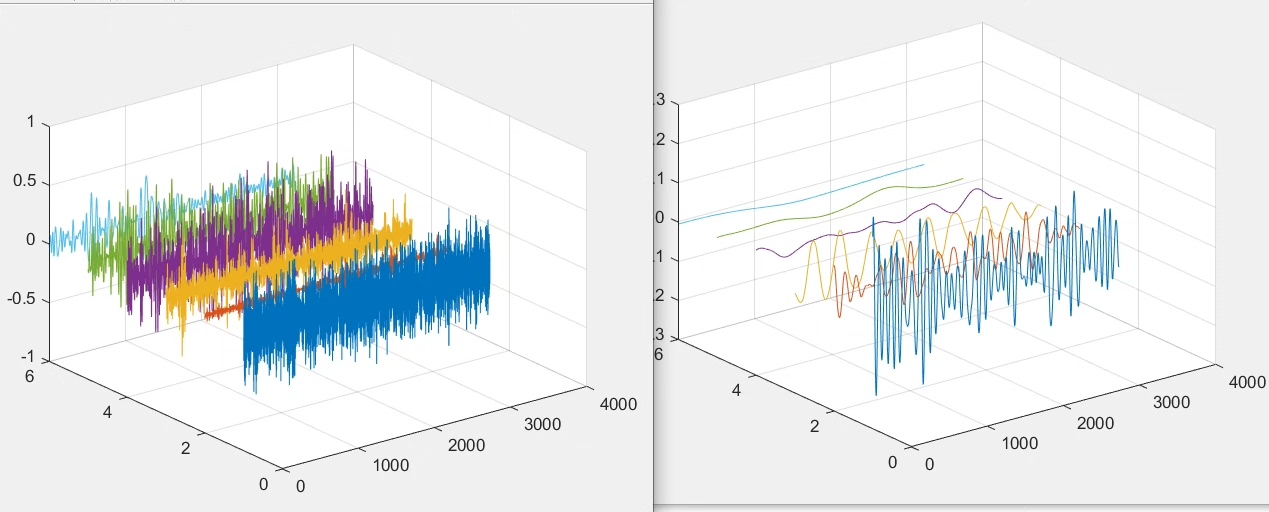
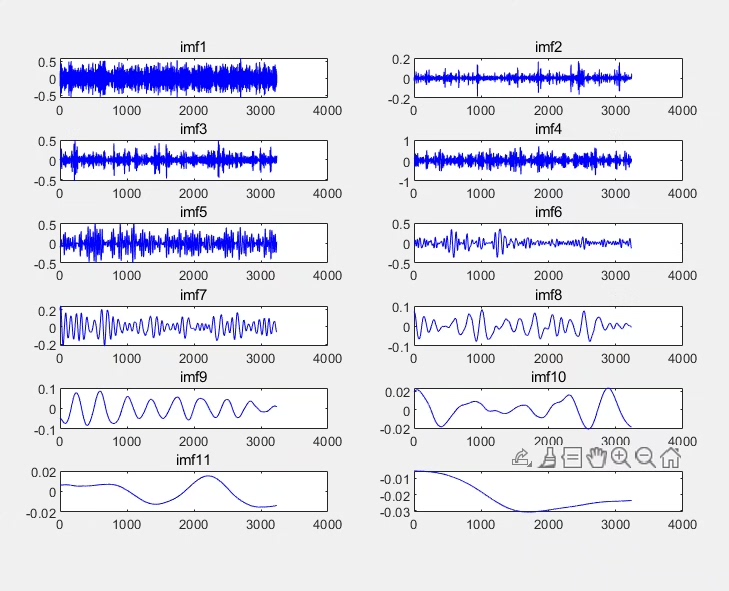
CEEMDAN-SE(自适应噪声完备集合经验模分解-样本熵信号重构) 结合CEEMDAN对信号进行分解,计算分解信号样本熵值,根据其大小重构为高中低频信号 可出信号分解图、三维分解图、频谱图、重构后的分解图、频谱图 程序有详细的使用说明: 1.输入信号data 2.进行CEEMDAN分解 3.根据样本熵值进行重构,其阈值可根据需求/实际情况进行修改 4.重构结果为高中低三个序列,绘制其信号及其频谱 matlab代码,含有部分注释; 数据为excel数据,使用时替换数据集即可; matlab代码,含有部分注释; 数据为excel数据,使用时替换数据集即可;
在信号处理的奇妙世界里,CEEMDAN - SE(自适应噪声完备集合经验模分解 - 样本熵信号重构)就像是一套神秘而强大的工具。今天咱们就来唠唠这 CEEMDAN - SE 到底是咋回事,顺便看看对应的 Matlab 代码。
一、CEEMDAN - SE 原理简单说
CEEMDAN 呢,就是把信号分解成一堆不同频率的固有模态函数(IMF)。就好比把一个复杂的音乐旋律,拆分成一个个简单的音符片段。然后通过计算这些分解出来信号的样本熵值,样本熵可以理解为衡量信号复杂度的一个指标,复杂度越高熵值越大。根据样本熵值的大小,我们就能把这些 IMF 重新组合,构建出高中低频信号,就像重新把音符排列成不同节奏的旋律。
二、Matlab 代码实现及分析
咱们直接上代码,假设已经把 excel 数据导入到 Matlab 环境中,数据存放在 data 变量里。
matlab
% 1. 读取数据,这里假设已经将 excel 数据读取到 data 变量
% 实际使用时,替换此数据集即可
% 2. 进行 CEEMDAN 分解
imf = ceemdan(data);
% ceemdan 函数是 Matlab 中用于执行 CEEMDAN 分解的关键函数
% 它会将输入的信号 data 分解成多个固有模态函数(IMF),存放在 imf 矩阵中
% 每一行对应一个 IMF 分量
% 3. 计算样本熵值并重构
for i = 1:size(imf, 1)
SampEn(i) = sampen(imf(i, :), 2, 0.2 * std(imf(i, :)));
end
% sampen 函数用于计算样本熵
% 这里对每个 IMF 分量计算样本熵,存储在 SampEn 数组中
% 根据样本熵值重构,这里设定一个简单的阈值,实际使用可按需修改
threshold1 = mean(SampEn) + std(SampEn);
threshold2 = mean(SampEn) - std(SampEn);
high_freq = [];
mid_freq = [];
low_freq = [];
for i = 1:size(imf, 1)
if SampEn(i) > threshold1
high_freq = high_freq + imf(i, :);
elseif SampEn(i) < threshold2
low_freq = low_freq + imf(i, :);
else
mid_freq = mid_freq + imf(i, :);
end
end
% 根据设定的阈值,将 IMF 分量分别累加到高中低频信号中
% 4. 绘制信号及其频谱
figure;
subplot(3, 1, 1);
plot(high_freq);
title('高频信号');
subplot(3, 1, 2);
plot(mid_freq);
title('中频信号');
subplot(3, 1, 3);
plot(low_freq);
title('低频信号');
figure;
subplot(3, 1, 1);
Pxx1 = periodogram(high_freq);
plot(1:length(Pxx1), Pxx1);
title('高频信号频谱');
subplot(3, 1, 2);
Pxx2 = periodogram(mid_freq);
plot(1:length(Pxx2), Pxx2);
title('中频信号频谱');
subplot(3, 1, 3);
Pxx3 = periodogram(low_freq);
plot(1:length(Pxx3), Pxx3);
title('低频信号频谱');三、结果展示
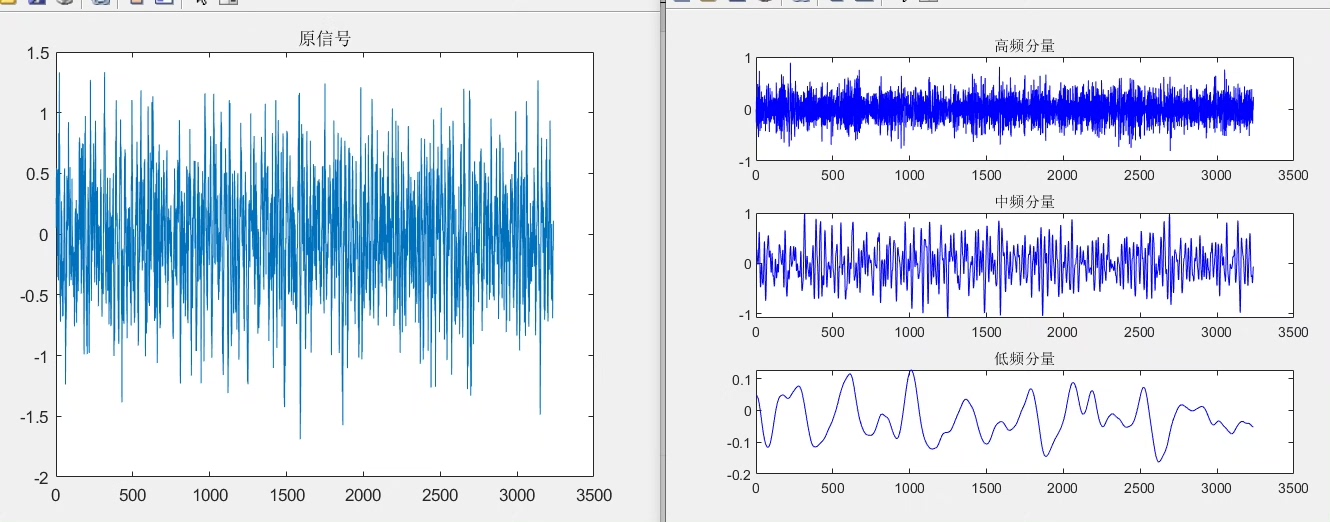
按照这个流程,我们就能得到信号分解图、三维分解图(代码里没详细展示绘制三维图,实际可通过一些 Matlab 函数实现,像 plot3 等函数结合 IMF 数据绘制)、频谱图、重构后的分解图、频谱图。这些图能帮助我们清晰地看到信号在不同频率段的特性,就像用放大镜去观察信号的不同细节。
四、使用说明回顾
- 第一步就是输入信号 data,这个 data 就是从 excel 数据读取过来的,实际应用直接替换就行。
- 接着进行 CEEMDAN 分解,调用 ceemdan 函数,Matlab 就会帮我们把信号分解成 IMF 分量。
- 计算样本熵值重构这步,关键在于那个阈值,阈值要根据实际需求和信号特点来调整,它决定了哪些 IMF 会被归到高中低频信号里。
- 最后重构结果是高中低三个序列,绘制它们的信号图和频谱图,直观地了解信号特性。
CEEMDAN - SE 这套组合在信号处理领域真的很实用,无论是在科研还是工程应用中,都能帮我们把复杂信号"看透",大家不妨动手试试,说不定能在自己的项目里挖掘出更多信号背后的秘密。